Introduction au t-SNE

t-SNE vs PCA

Le t-SNE et l'ACP sont des techniques de réduction dimensionnelle qui ont des mécanismes différents et fonctionnent mieux avec différents types de données.

L'ACP (analyse en composantes principales) est une technique linéaire qui fonctionne le mieux avec des données ayant une structure linéaire. Elle cherche à identifier les composantes principales sous-jacentes des données en les projetant sur des dimensions inférieures, en minimisant la variance et en préservant les grandes distances entre les paires. Lisez notre tutoriel sur l 'analyse en composantes principales (ACP) pour comprendre le fonctionnement interne des algorithmes à l'aide d'exemples R. 

Mais le t-SNE est une technique non linéaire qui se concentre sur la préservation des similarités par paire entre les points de données dans un espace de dimension inférieure. Le t-SNE s'attache à préserver les petites distances par paire alors que l'ACP se concentre sur le maintien de grandes distances par paire afin de maximiser la variance.

En résumé, l'ACP préserve la variance des données, tandis que le t-SNE préserve les relations entre les points de données dans un espace de moindre dimension, ce qui en fait un bon algorithme pour la visualisation de données complexes à haute dimension. 

Comment fonctionne le t-SNE

L'algorithme t-SNE trouve la mesure de similarité entre les paires d'instances dans un espace de dimension supérieure et inférieure. Ensuite, il tente d'optimiser deux mesures de similarité. Tout cela se fait en trois étapes. 

1. Le t-SNE modélise la sélection d'un point comme voisin d'un autre point dans les dimensions supérieures et inférieures. Il commence par calculer une similarité par paire entre tous les points de données dans l'espace à haute dimension à l'aide d'un noyau gaussien. Les points éloignés les uns des autres ont une probabilité plus faible d'être choisis que les points proches les uns des autres. 
2. Ensuite, l'algorithme tente de cartographier les points de données de haute dimension dans un espace de dimension inférieure tout en préservant les similitudes par paire. 
3. Il s'agit de minimiser la divergence entre la distribution de probabilité de la haute dimension d'origine et celle de la basse dimension. L'algorithme utilise la descente de gradient pour minimiser la divergence. L'intégration de la dimension inférieure est optimisée jusqu'à un état stable.

Le processus d'optimisation permet de créer des grappes et des sous-grappes de points de données similaires dans l'espace de dimension inférieure, qui sont visualisées pour comprendre la structure et les relations dans les données de dimension supérieure. 

t-SNE Exemple Python

Dans l'exemple Python, nous allons générer des données de classification, effectuer une ACP et un t-SNE, et visualiser les résultats. Pour la réduction de la dimensionnalité, nous utiliserons Scikit-Learn, et pour la visualisation, nous utiliserons Plotly Express. 

Génération d'un ensemble de données de classification

Nous utiliserons la fonction make_classification de Scikit-Learn pour générer des données synthétiques avec 6 caractéristiques, 1500 échantillons et 3 classes. 

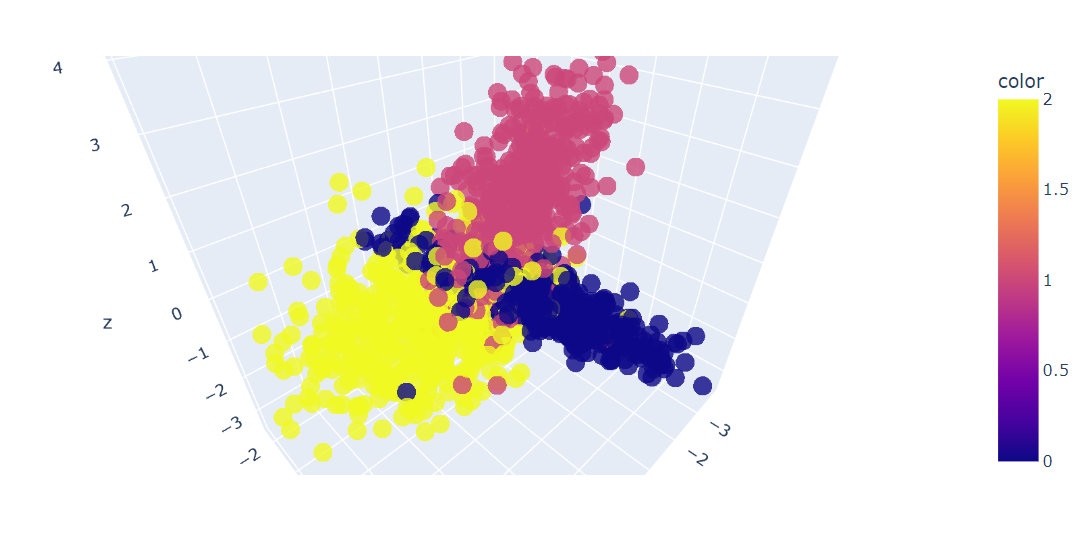
Ensuite, nous tracerons en 3D les trois premières caractéristiques des données à l'aide de la fonction Plotly Express scatter_3d. 

import plotly.express as px
from sklearn.datasets import make_classification

X, y = make_classification(
    n_features=6,
    n_classes=3,
    n_samples=1500,
    n_informative=2,
    random_state=5,
    n_clusters_per_class=1,
)


fig = px.scatter_3d(x=X[:, 0], y=X[:, 1], z=X[:, 2], color=y, opacity=0.8)
fig.show()

Nous avons un graphique en 3D des données ; vous pouvez également visualiser les données dans un graphique en 2D en utilisant la fonction Plotly Express scatter.

Ajustement et transformation de l'ACP

Nous allons maintenant appliquer l'algorithme PCA à l'ensemble de données pour obtenir deux composantes PCA. Le site fit_transform apprend et transforme l'ensemble de données en même temps.  

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

Visualisation t-SNE Python

Nous pouvons maintenant visualiser les résultats en affichant deux composantes de l'ACP sur un diagramme de dispersion. 

• x : Première composante
• y : Deuxième compagnon
• couleur : variable cible.

Nous avons également utilisé la fonction update_layout pour ajouter un titre et renommer les axes x et y.

fig = px.scatter(x=X_pca[:, 0], y=X_pca[:, 1], color=y)
fig.update_layout(
    title="PCA visualization of Custom Classification dataset",
    xaxis_title="First Principal Component",
    yaxis_title="Second Principal Component",
)
fig.show()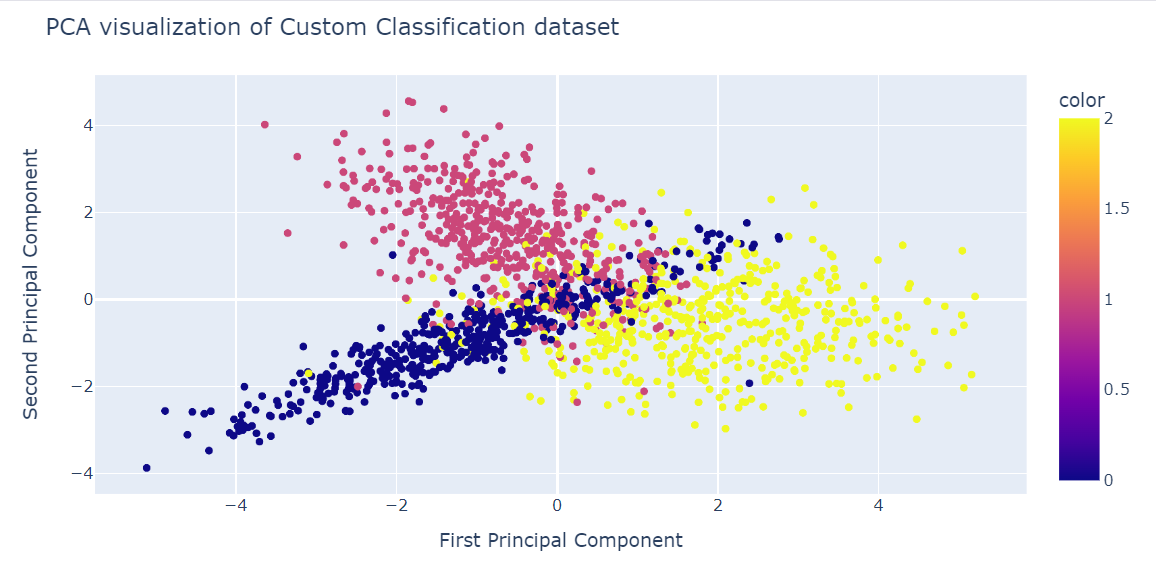

Ajustement et transformation t-SNE

Nous allons maintenant appliquer l'algorithme t-SNE à l'ensemble de données et comparer les résultats. 

Après avoir ajusté et transformé les données, nous afficherons la divergence de Kullback-Leibler (KL) entre la distribution de probabilité à haute dimension et la distribution de probabilité à basse dimension. 

Une faible divergence KL est le signe de meilleurs résultats.

from sklearn.manifold import TSNE

tsne = TSNE(n_components=2, random_state=42)
X_tsne = tsne.fit_transform(X)
tsne.kl_divergence_

1.1169137954711914

Visualisation t-SNE Python

Comme pour l'ACP, nous visualiserons deux composantes du SNEt sur un diagramme de dispersion. 

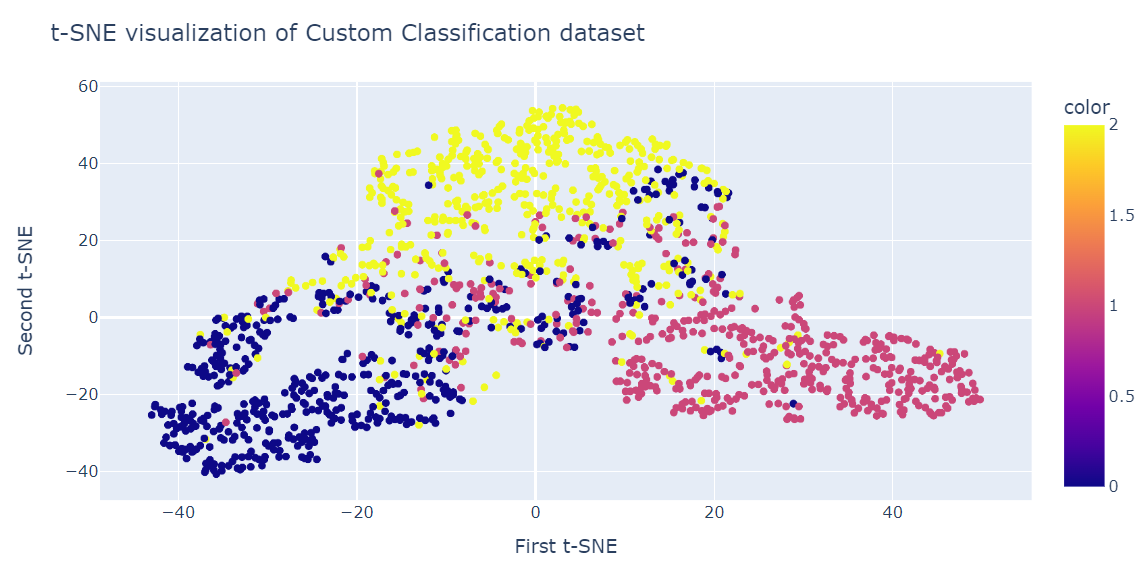
fig = px.scatter(x=X_tsne[:, 0], y=X_tsne[:, 1], color=y)
fig.update_layout(
    title="t-SNE visualization of Custom Classification dataset",
    xaxis_title="First t-SNE",
    yaxis_title="Second t-SNE",
)
fig.show()

Le résultat est bien meilleur que celui de l'ACP. Nous pouvons clairement voir trois grands groupes. 

t-SNE sur l'ensemble des données relatives au désabonnement des clients

Dans cette section, nous utiliserons l'ensemble de données réelles sur le taux d'attrition des clients d'une société de télécommunications iranienne. L'ensemble de données contient des informations sur l'activité des clients, telles que les échecs d'appel et la durée de l'abonnement, ainsi qu'une étiquette de désabonnement.

Le taux d'attrition est le pourcentage de clients qui cessent d'utiliser un service particulier pendant une période donnée.

Note : La source du code et l'ensemble des données des deux exemples sont disponibles dans ce classeur DataLab; si vous souhaitez modifier et exécuter le code, il vous suffit d'en faire une copie et c'est parti !

Importation d'un ensemble de données sur le taux d'attrition des clients

Nous allons charger le jeu de données à l'aide de pandas et afficher les trois premières lignes.

import pandas as pd

df = pd.read_csv("data/customer_churn.csv")
df.head(3)

Réduction de la dimensionnalité de l'ACP

Ensuite, nous le ferons :

• Créez des caractéristiques (X) et des cibles (y) à l'aide de la colonne Churn.
• Normalisez les caractéristiques à l'aide d'une échelle standard.
• Divisez l'ensemble de données en un ensemble de formation et un ensemble de test.
• Appliquez l'ACP à l'ensemble de données d'apprentissage.
• Obtenez le score en utilisant l'ensemble de données de test. Le score représente la log-vraisemblance moyenne de tous les échantillons.

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

X = df.drop('Churn', axis=1)
y = df['Churn']

scaler = StandardScaler()
X_norm = scaler.fit_transform(X)

X_train, X_test, y_train, y_test = train_test_split(
    X_norm, y, random_state=13, test_size=0.25, shuffle=True
)

pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train)

pca.score(X_test)

-17.04482851288105

Visualisation de l'ACP

Nous allons maintenant visualiser le résultat de l'ACP à l'aide du diagramme de dispersion Plotly Express. 

fig = px.scatter(x=X_train_pca[:, 0], y=X_train_pca[:, 1], color=y_train)
fig.update_layout(
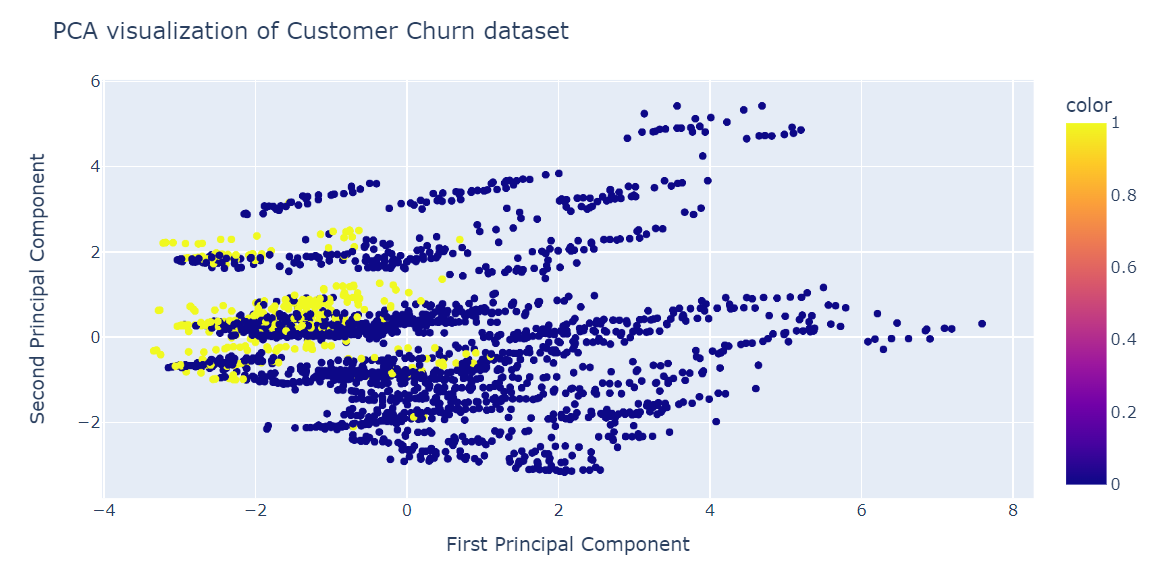
    title="PCA visualization of Customer Churn dataset",
    xaxis_title="First Principal Component",
    yaxis_title="Second Principal Component",
)
fig.show()

L'ACP n'a pas permis de créer des grappes. Les données dans la dimension inférieure semblent aléatoires. Cela peut également signifier que les caractéristiques de l'ensemble de données sont très asymétriques ou qu'il n'y a pas de structure de corrélation forte. 

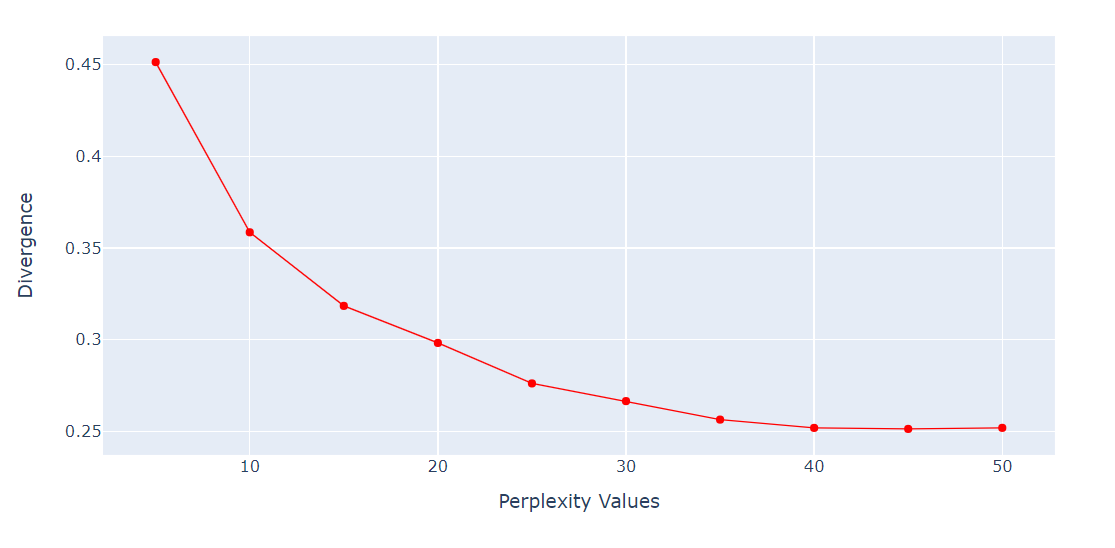
Vérification de la perplexité vs. Divergence

Pour l'algorithme t-SNE, la perplexité est un hyperparamètre très important. Il contrôle le nombre effectif de voisins que chaque point prend en compte au cours du processus de réduction de la dimensionnalité. 

Nous exécuterons une boucle pour obtenir la métrique de la divergence KL sur différentes perplexités allant de 5 à 55 avec un écart de 5 points. Ensuite, nous afficherons le résultat à l'aide du tracé linéaire de Plotly Express.

import numpy as np

perplexity = np.arange(5, 55, 5)
divergence = []

for i in perplexity:
    model = TSNE(n_components=2, init="pca", perplexity=i)
    reduced = model.fit_transform(X_train)
    divergence.append(model.kl_divergence_)
fig = px.line(x=perplexity, y=divergence, markers=True)
fig.update_layout(xaxis_title="Perplexity Values", yaxis_title="Divergence")
fig.update_traces(line_color="red", line_width=1)
fig.show()

La divergence KL est devenue constante après 40 perplexités. Nous utiliserons donc une perplexité de 40 dans l'algorithme t-SNE.  

t-SNE Réduction de la dimensionnalité

Nous allons maintenant ajuster t-SNE et transformer les données en dimensions inférieures en utilisant 40 perplexités pour obtenir la plus faible divergence de KL. 

from sklearn.manifold import TSNE

tsne = TSNE(n_components=2,perplexity=40, random_state=42)
X_train_tsne = tsne.fit_transform(X_train)

tsne.kl_divergence_

0.258713960647583

Visualisation du t-SNE

Nous allons maintenant utiliser le diagramme de dispersion Plotly pour afficher les composants et les classes cibles. 

fig = px.scatter(x=X_train_tsne[:, 0], y=X_train_tsne[:, 1], color=y_train)
fig.update_layout(
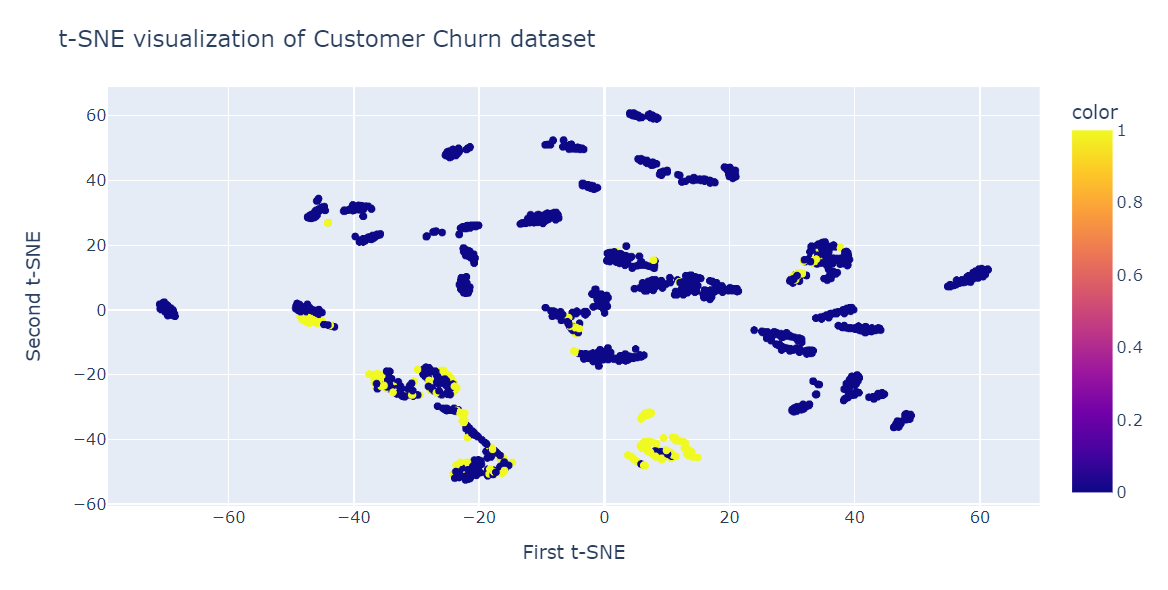
    title="t-SNE visualization of Customer Churn dataset",
    xaxis_title="First t-SNE",
    yaxis_title="Second t-SNE",
)
fig.show()

Comme vous pouvez le constater, nous avons plusieurs groupes et sous-groupes. Nous pouvons utiliser ces informations pour comprendre le modèle et élaborer une stratégie de fidélisation des clients existants. 

Application de t-SNE

Outre la visualisation de données multidimensionnelles complexes, l'ENT-T a d'autres utilisations, principalement dans le domaine médical. 

1. Regroupement et classification : pour regrouper des points de données similaires dans un espace de moindre dimension. Il peut également être utilisé pour la classification et la recherche de modèles dans les données. 
2. Détection des anomalies : pour identifier les valeurs aberrantes et les anomalies dans les données. 
3. Traitement du langage naturel : visualisation des enchâssements de mots générés à partir d'un vaste corpus de textes, ce qui facilite l'identification des similitudes et des relations entre les mots.
4. Sécurité informatique : pour visualiser les schémas de trafic du réseau et détecter les anomalies.
5. Recherche sur le cancer : pour visualiser les profils moléculaires des échantillons de tumeurs et identifier les sous-types de cancer. 
6. Interprétation du domaine géologique : visualisation des attributs sismiques et identification des anomalies géologiques. 
7. Traitement des signaux biomédicaux : pour visualiser l'électroencéphalogramme (EEG) et détecter les schémas d'activité cérébrale. 

Conclusion

Le t-SNE est un outil de visualisation puissant qui permet de révéler des modèles et des structures cachés dans des ensembles de données complexes. Vous pouvez l'utiliser pour les images, les sons, les données biologiques et les données individuelles afin d'identifier les anomalies et les modèles. 

Dans cet article de blog, nous avons découvert le t-SNE, une technique populaire de réduction de la dimensionnalité qui permet de visualiser des données non linéaires de haute dimension dans un espace de faible dimension. Nous avons expliqué l'idée principale du t-SNE, son fonctionnement et ses applications. En outre, nous avons montré quelques exemples d'application de t-SNE à des synthèses et à des ensembles de données réels, ainsi que la manière d'interpréter les résultats. 

Le t-SNE fait partie de l'apprentissage non supervisé, et la prochaine étape naturelle est de comprendre le regroupement hiérarchique, l'ACP, la décorrélation et la découverte de caractéristiques interprétables. Apprenez tous les sujets en suivant notre cours Apprentissage non supervisé en Python.