Course
In this tutorial, we will get into the workings of t-SNE, a powerful technique for dimensionality reduction and data visualization. We will compare it with another popular technique, PCA, and demonstrate how to perform both t-SNE and PCA using scikit-learn and plotly express on synthetic and real-world datasets.
What is t-SNE ?
t-SNE (t-distributed Stochastic Neighbor Embedding) is an unsupervised non-linear dimensionality reduction technique for data exploration and visualizing high-dimensional data. Non-linear dimensionality reduction means that the algorithm allows us to separate data that cannot be separated by a straight line.

t-SNE gives you a feel and intuition on how data is arranged in higher dimensions. It is often used to visualize complex datasets into two and three dimensions, allowing us to understand more about underlying patterns and relationships in the data.
Take our Dimensionality Reduction in Python course to learn about exploring high-dimensional data, feature selection, and feature extraction.
Become a ML Scientist
t-SNE vs PCA
Both t-SNE and PCA are dimensional reduction techniques with different mechanisms that work best with different types of data.
PCA (Principal Component Analysis) is a linear technique that works best with data that has a linear structure. It seeks to identify the underlying principal components in the data by projecting onto lower dimensions, minimizing variance, and preserving large pairwise distances. Read our Principal Component Analysis (PCA) tutorial to understand the inner workings of the algorithms with R examples.
But, t-SNE is a nonlinear technique that focuses on preserving the pairwise similarities between data points in a lower-dimensional space. t-SNE is concerned with preserving small pairwise distances whereas, PCA focuses on maintaining large pairwise distances to maximize variance.
In summary, PCA preserves the variance in the data. In contrast, t-SNE preserves the relationships between data points in a lower-dimensional space, making it quite a good algorithm for visualizing complex high-dimensional data.
The following table can help you compare t-SNE and PCA side by side:
| Characteristic | t-SNE | PCA |
|---|---|---|
| Type | Non-linear dimensionality reduction | Linear dimensionality reduction |
| Goal | Preserve local pairwise similarities | Preserve global variance |
| Best used for | Visualizing complex, high-dimensional data | Data with linear structure |
| Output | Low-dimensional representation | Principal components |
| Use cases | Clustering, anomaly detection, NLP | Noise reduction, feature extraction |
| Computational intensity | High | Low |
| Interpretation | Harder to interpret | Easier to interpret |
How t-SNE Works
The t-SNE algorithm finds the similarity measure between pairs of instances in higher and lower dimensional space. After that, it tries to optimize two similarity measures. It does all of that in three steps.
- t-SNE models a point being selected as a neighbor of another point in both higher and lower dimensions. It starts by calculating a pairwise similarity between all data points in the high-dimensional space using a Gaussian kernel. The points far apart have a lower probability of being picked than the points close together.
- The algorithm then tries to map higher-dimensional data points onto lower-dimensional space while preserving the pairwise similarities.
- It is achieved by minimizing the divergence between the original high-dimensional and lower-dimensional probability distribution. The algorithm uses gradient descent to minimize the divergence. The lower-dimensional embedding is optimized to a stable state.
The optimization process allows the creation of clusters and sub-clusters of similar data points in the lower-dimensional space, which are visualized to understand the structure and relationships in the higher-dimensional data.
t-SNE Python Example
In the Python example, we will generate classification data, perform PCA and t-SNE, and visualize the results. We will use scikit-learn to perform dimensionality reduction, and we will use Plotly Express for visualization.
Generating a classification dataset
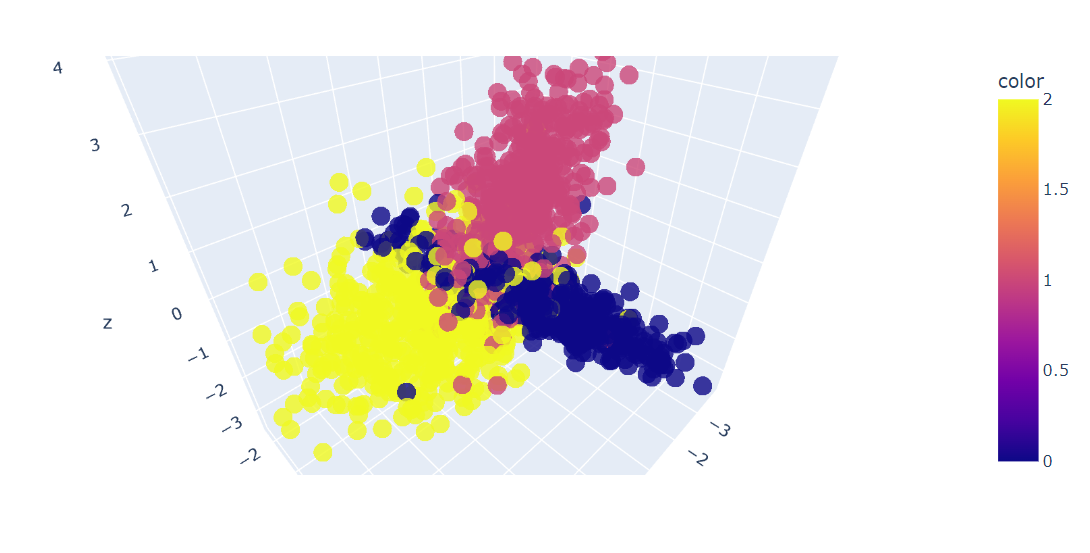
We will use scikit-learn’s make_classification() function to generate synthetic data with 6 features, 1500 samples, and 3 classes.
After that, we will 3D plot the first three features of the data using the Plotly Express scatter_3d() function.
import plotly.express as px
from sklearn.datasets import make_classification
X, y = make_classification(
n_features=6,
n_classes=3,
n_samples=1500,
n_informative=2,
random_state=5,
n_clusters_per_class=1,
)
fig = px.scatter_3d(x=X[:, 0], y=X[:, 1], z=X[:, 2], color=y, opacity=0.8)
fig.show()We have a 3D plot of the data; you can also visualize the data in a 2D chart by using the Plotly Express scatter() function.
Fitting and transforming with PCA
We will now apply the PCA algorithm on the dataset to return two PCA components. The fit_transform() learns and transforms the dataset at the same time.
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)t-SNE visualization in Python
We can now visualize the results by displaying two PCA components on a scatter plot.
- x: First component
- y: Second companion
- color: target variable.
We have also used the update_layout() function to add a title and rename the x-axis and y-axis.
fig = px.scatter(x=X_pca[:, 0], y=X_pca[:, 1], color=y)
fig.update_layout(
title="PCA visualization of Custom Classification dataset",
xaxis_title="First Principal Component",
yaxis_title="Second Principal Component",
)
fig.show()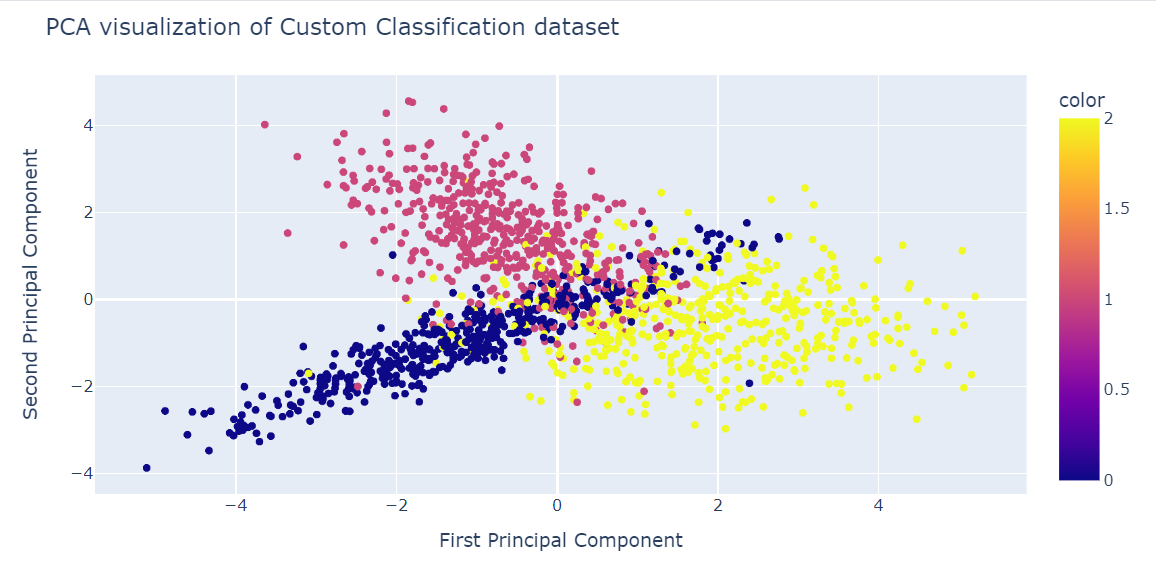
Fitting and transforming the t-SNE
Now, we will apply the t-SNE algorithm to the dataset and compare the results.
After fitting and transforming data, we will display the Kullback-Leibler (KL) divergence between the high and low-dimensional probability distributions. Low KL divergence is normally a sign of better results.
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, random_state=42)
X_tsne = tsne.fit_transform(X)
tsne.kl_divergence_1.1169137954711914t-SNE visualization in Python
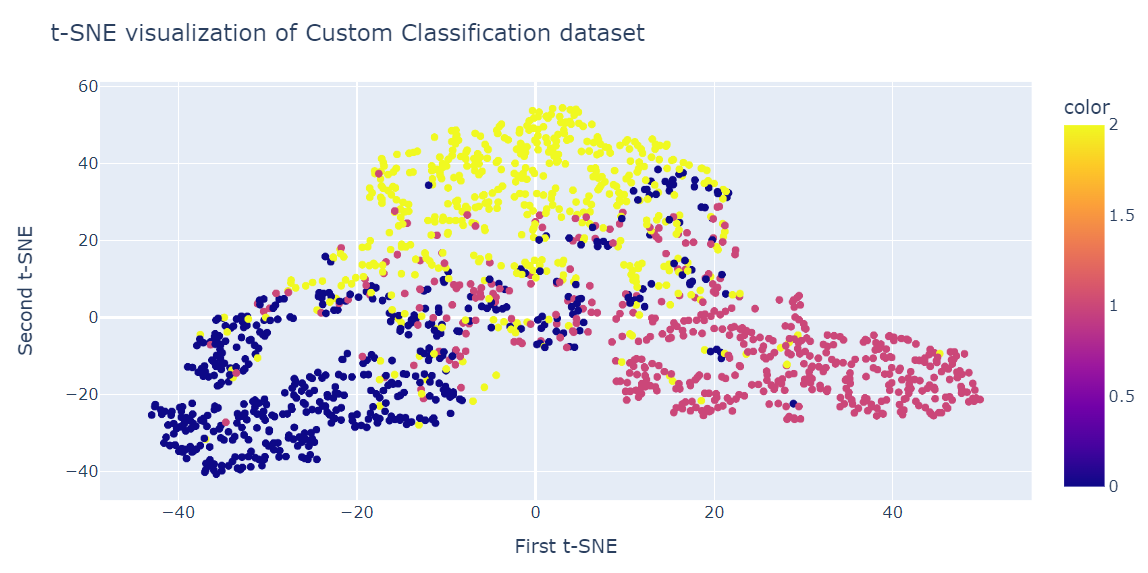
Similar to PCA, we will visualize two t-SNE components on a scatter plot.
fig = px.scatter(x=X_tsne[:, 0], y=X_tsne[:, 1], color=y)
fig.update_layout(
title="t-SNE visualization of Custom Classification dataset",
xaxis_title="First t-SNE",
yaxis_title="Second t-SNE",
)
fig.show()The result is quite better than PCA. We can clearly see three big clusters.
t-SNE on a Customer Churn Dataset
In this section, we will use an Iranian telecom company's customer churn dataset. The dataset contains information on customers' activity, such as call failures and subscription length, and a churn label.
Churn means the percentage of customers that stop using a particular service during a given time frame.
Note: The code source and dataset from both examples are available in this DataLab workbook; if you want to tweak and run the code, just make a copy, and you're good to go!
Importing the customer churn dataset
We will load the dataset using pandas and display the first three rows.
import pandas as pd
df = pd.read_csv("data/customer_churn.csv")
df.head(3)
PCA dimensionality reduction
After that, we will:
- Create features (X) and target (y) using the Churn column.
- Normalize the features using a standard scaler.
- Split the dataset into a training and testing set.
- Apply PCA to the training dataset.
- Get the score using the testing dataset. The score represents the average log-likelihood of all samples.
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
X = df.drop('Churn', axis=1)
y = df['Churn']
scaler = StandardScaler()
X_norm = scaler.fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(
X_norm, y, random_state=13, test_size=0.25, shuffle=True
)
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train)
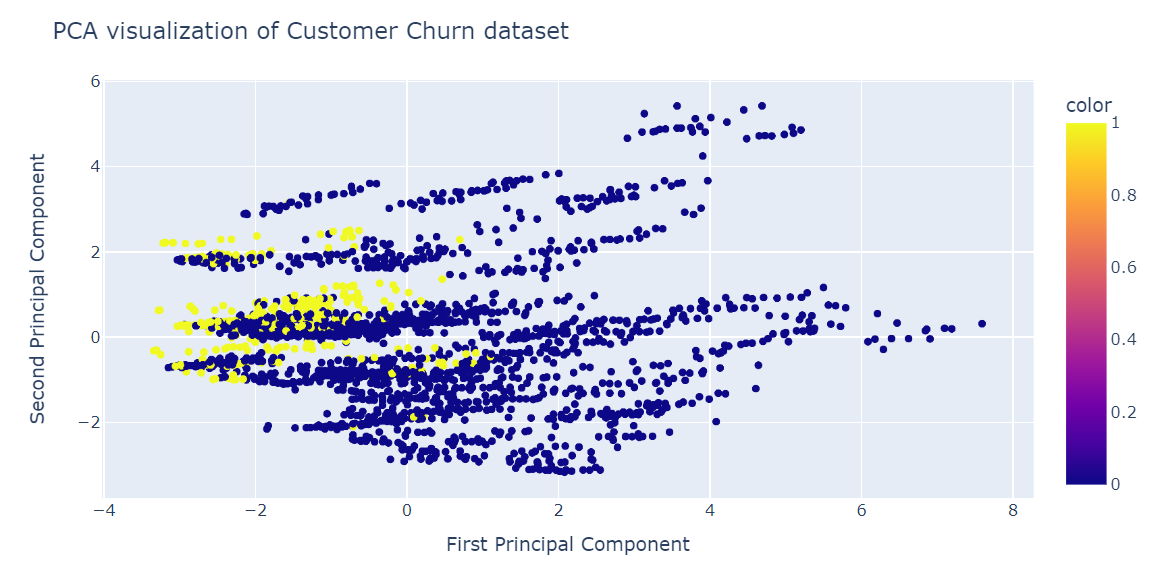
pca.score(X_test)-17.04482851288105Visualizing the PCA results
We will now visualize the PCA result using the Plotly Express scatter plot.
fig = px.scatter(x=X_train_pca[:, 0], y=X_train_pca[:, 1], color=y_train)
fig.update_layout(
title="PCA visualization of Customer Churn dataset",
xaxis_title="First Principal Component",
yaxis_title="Second Principal Component",
)
fig.show()PCA was not good at creating clusters. The data in the low dimension looks random. It could also mean the features in the dataset are highly skewed, or it does not have a strong correlation structure.
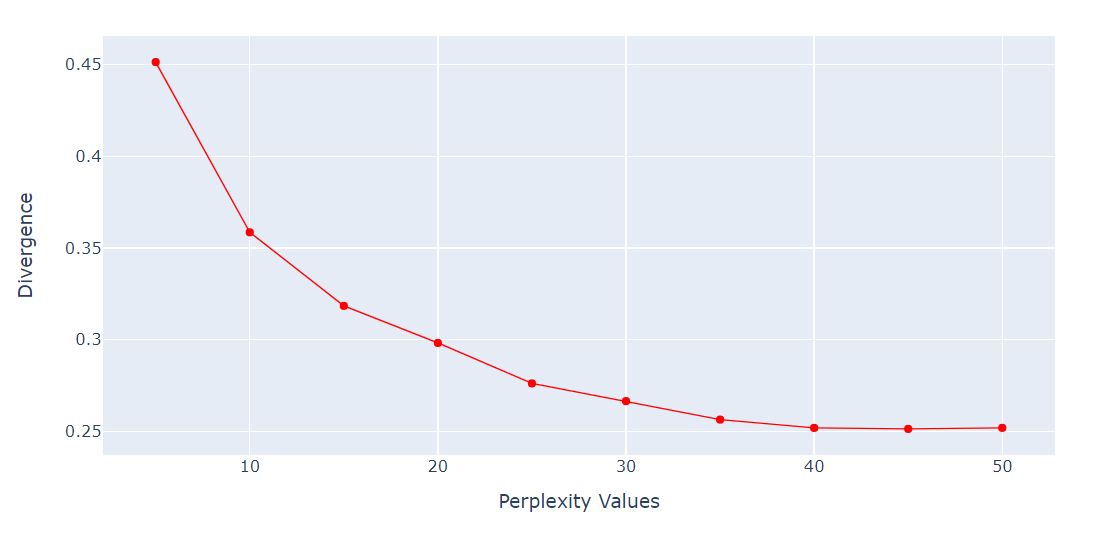
Checking perplexity vs. divergence
Perplexity is an important hyperparameter for the t-SNE algorithm. It controls the effective number of neighbors that each point considers during the dimensionality reduction process.
We will run a loop to get the KL Divergence metric on various perplexities from 5 to 55 with a 5-point gap. Then, we will display the result using the Plotly Express line plot.
import numpy as np
perplexity = np.arange(5, 55, 5)
divergence = []
for i in perplexity:
model = TSNE(n_components=2, init="pca", perplexity=i)
reduced = model.fit_transform(X_train)
divergence.append(model.kl_divergence_)
fig = px.line(x=perplexity, y=divergence, markers=True)
fig.update_layout(xaxis_title="Perplexity Values", yaxis_title="Divergence")
fig.update_traces(line_color="red", line_width=1)
fig.show()The KL Divergence has become constant after 40 perplexity. So, we will use 40 perplexity in the t-SNE algorithm.
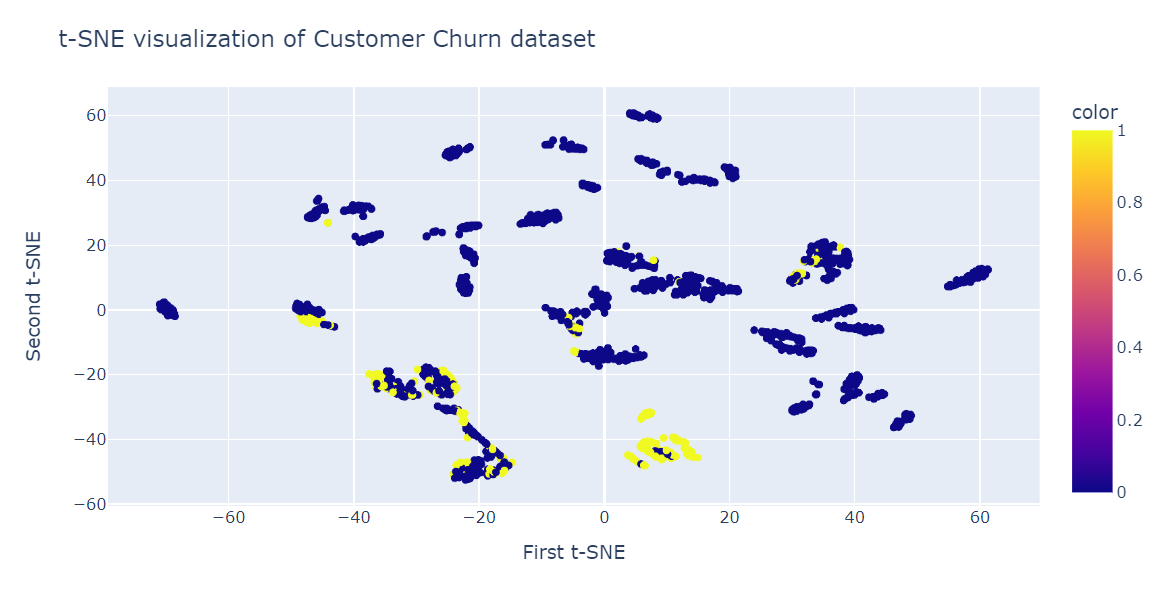
t-SNE dimensionality reduction
We will now fit t-SNE and transform the data into lower dimensions using 40 perplexity to get the lowest KL Divergence.
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2,perplexity=40, random_state=42)
X_train_tsne = tsne.fit_transform(X_train)
tsne.kl_divergence_0.258713960647583Visualizing the t-SNE
We will now use the Plotly Scatter plot to display components and target classes.
fig = px.scatter(x=X_train_tsne[:, 0], y=X_train_tsne[:, 1], color=y_train)
fig.update_layout(
title="t-SNE visualization of Customer Churn dataset",
xaxis_title="First t-SNE",
yaxis_title="Second t-SNE",
)
fig.show()As we can see, we have multiple clusters and sub-clusters. We can use this information to understand the pattern and develop a strategy for retaining existing customers.
Limitations and Challenges of t-SNE
While t-SNE is a powerful visualization tool for high-dimensional data, it comes with some limitations:
- Computational cost: t-SNE is computationally expensive, especially for large datasets. Its pairwise similarity calculations scale poorly with the size of the dataset, making it less suitable for datasets with millions of points.
- Sensitivity to hyperparameters: The performance of t-SNE is highly dependent on hyperparameters like perplexity and learning rate. Finding the optimal values often requires trial and error, which can be time-consuming.
- Lack of interpretability: The resulting embeddings in t-SNE are often non-deterministic (due to random initialization and gradient descent) and lack a direct interpretable relationship with the original high-dimensional data.
- Not suitable for out-of-sample data: t-SNE cannot generalize to new, unseen data without re-computing the embeddings from scratch, which is inefficient for dynamic datasets.
t-SNE vs. UMAP: A comparison
In recent years, UMAP (Uniform Manifold Approximation and Projection) has emerged as a popular alternative to t-SNE. While both are non-linear dimensionality reduction techniques designed for visualization, UMAP addresses some of the limitations of t-SNE:
- UMAP is faster and more memory-efficient than t-SNE, making it suitable for large datasets.
- UMAP is better at preserving both local and global structures in the data, while t-SNE primarily focuses on preserving local pairwise similarities.
- UMAP has fewer hyperparameters to tune compared to t-SNE, and its results are generally more consistent across runs.
- Unlike t-SNE, UMAP supports transformations for new data points, making it more suitable for dynamic datasets.
Computational complexity: t-SNE vs. UMAP vs. PCA
The following table summarizes the computational complexity of t-SNE compared to UMAP and PCA:
| Technique | Computational complexity | Features | Suitability for large datasets |
|---|---|---|---|
| t-SNE | O(N2) | Preserves local structure, highly customizable | Moderate (slow for large datasets) |
| UMAP | O(N log N) | Balances local and global structure, faster | High (handles large datasets efficiently) |
| PCA | O(Nd2) | Linear reduction, interpretable components | High (very efficient) |
- N: Number of data points
- d: Number of features in the data
In summary, while t-SNE provides detailed insights into local relationships, UMAP is often a more efficient and scalable choice for modern datasets. PCA remains a fast and interpretable option for linear data. Depending on the dataset and goals, choosing the right technique involves balancing interpretability, computational cost, and the nature of the data.
Applications of t-SNE
Apart from visualizing complex multi-dimensional data, t-SNE has other uses:
- Clustering and classification: to cluster similar data points together in lower dimensional space. It can also be used for classification and finding patterns in the data.
- Anomaly detection: to identify outliers and anomalies in the data.
- Natural language processing: to visualize word embeddings generated from a large corpus of text that makes it easier to identify similarities and relationships between words.
- Computer security: to visualize network traffic patterns and detect anomalies.
- Cancer research: to visualize molecular profiles of tumor samples and identify cancer subtypes.
- Geological domain interpretation: to visualize seismic attributes and to identify geological anomalies.
- Biomedical signal processing: to visualize electroencephalogram (EEG) and detect patterns of brain activity.
Conclusion
t-SNE is a powerful visualization tool for revealing hidden patterns and structures in complex datasets. You can use it for images, audio, biologicals, and single data to identify anomalies and patterns.
In this blog post, we have learned about t-SNE, a popular dimensionality reduction technique that can visualize high-dimensional non-linear data in a low-dimensional space. We have explained the main idea behind t-SNE, how it works, and its applications. Moreover, we have shown some examples of applying t-SNE to synthetic and real datasets and how to interpret the results.
t-SNE is a part of Unsupervised Learning, and the next natural step is to understand hierarchical clustering, PCA, Decorrelating, and discovering interpretable features. Learn all of the topics by taking our Unsupervised Learning in Python course.
Build Machine Learning Skills
FAQs
Can t-SNE be used for large datasets, and what are the limitations?
t-SNE can struggle with very large datasets due to its computational complexity and memory usage. It's often recommended to use t-SNE on a subset of the data or consider alternatives like UMAP for larger datasets.
How does the choice of perplexity affect the results of t-SNE?
Perplexity is a crucial hyperparameter in t-SNE that influences the balance between local and global data structure preservation. Low perplexity emphasizes local relationships, while high perplexity captures broader structures. Experimenting with different values is often necessary to find the optimal setting for your data.
What other hyperparameters should I consider tuning in t-SNE, besides perplexity?
Besides perplexity, you should consider the learning rate and the number of iterations. The learning rate affects how quickly the algorithm converges, while the number of iterations determines the duration of the optimization process.
How does t-SNE handle noise in the data?
t-SNE can be sensitive to noise as it tries to preserve pairwise similarities, which can be distorted by noisy features. Preprocessing steps such as feature selection or denoising can help improve t-SNE results.
Can t-SNE results be used for quantitative analysis, such as clustering?
t-SNE is primarily a visualization tool and not ideal for quantitative analysis or clustering since it doesn't preserve true distances or densities. For clustering, techniques like K-means or DBSCAN should be applied to the original high-dimensional data.
Is there a way to improve the interpretability of t-SNE plots?
To enhance interpretability, you can label the data points with known categories, use interactive plots, or overlay additional information like cluster boundaries or centroids.
How does t-SNE compare to UMAP in terms of performance and results?
UMAP is often faster than t-SNE and can handle larger datasets with similar or better quality embeddings. UMAP also tends to preserve more of the global structure of the data compared to t-SNE.
Can t-SNE be integrated into a real-time data visualization pipeline?
Due to its computational intensity, t-SNE is generally not suited for real-time visualization. However, if the dataset size is manageable and updates are infrequent, it might be feasible with optimization and sampling.
How should one interpret the clusters formed in a t-SNE plot?
Clusters in a t-SNE plot indicate groups of data points with high similarity in the original high-dimensional space. However, the exact distances and shapes in t-SNE plots should not be overly interpreted as they are not meaningful in the same way as in the original space.
Are there any specific applications where t-SNE is particularly beneficial?
t-SNE is particularly useful in exploratory data analysis, such as visualizing gene expression profiles, image data, or word embeddings, where understanding the local structure and relationships is crucial.

As a certified data scientist, I am passionate about leveraging cutting-edge technology to create innovative machine learning applications. With a strong background in speech recognition, data analysis and reporting, MLOps, conversational AI, and NLP, I have honed my skills in developing intelligent systems that can make a real impact. In addition to my technical expertise, I am also a skilled communicator with a talent for distilling complex concepts into clear and concise language. As a result, I have become a sought-after blogger on data science, sharing my insights and experiences with a growing community of fellow data professionals. Currently, I am focusing on content creation and editing, working with large language models to develop powerful and engaging content that can help businesses and individuals alike make the most of their data.
