Introdução ao t-SNE

Neste tutorial, vamos nos aprofundar no funcionamento do t-SNE, uma técnica avançada para redução de dimensionalidade e visualização de dados. Vamos compará-lo com outra técnica popular, a PCA, e demonstrar como executar o t-SNE e a PCA usando o scikit-learn e o plotly express em conjuntos de dados sintéticos e do mundo real.

O que é t-SNE?

O t-SNE (t-distributed Stochastic Neighbor Embedding) é uma técnica não supervisionada de redução de dimensionalidade não linear para exploração de dados e visualização de dados de alta dimensão. A redução não linear da dimensionalidade significa que o algoritmo nos permite separar dados que não podem ser separados por uma linha reta. 

O t-SNE lhe dá uma sensação e uma intuição de como os dados são organizados em dimensões mais altas. Ele é usado com frequência para visualizar conjuntos de dados complexos em duas e três dimensões, o que nos permite entender melhor os padrões e as relações subjacentes nos dados.

Faça nosso curso de Redução de Dimensionalidade em Python para aprender a explorar dados de alta dimensão, seleção de recursos e extração de recursos.

t-SNE vs. PCA

Tanto o t-SNE quanto o PCA são técnicas de redução dimensional que têm mecanismos diferentes e funcionam melhor com diferentes tipos de dados.

A PCA (Análise de Componentes Principais) é uma técnica linear que funciona melhor com dados que têm uma estrutura linear. Ele busca identificar os componentes principais subjacentes nos dados, projetando-os em dimensões inferiores, minimizando a variação e preservando grandes distâncias entre pares. Leia nosso tutorial de análise de componentes principais (PCA) para entender o funcionamento interno dos algoritmos com exemplos em R. 

Porém, o t-SNE é uma técnica não linear que se concentra em preservar as semelhanças entre os pares de pontos de dados em um espaço de dimensão inferior. O t-SNE se preocupa em preservar pequenas distâncias entre pares, enquanto o PCA se concentra em manter grandes distâncias entre pares para maximizar a variação.

Em resumo, o PCA preserva a variação nos dados, enquanto o t-SNE preserva as relações entre os pontos de dados em um espaço de dimensão inferior, o que o torna um algoritmo muito bom para visualizar dados complexos de alta dimensão. 

Como o t-SNE funciona

O algoritmo t-SNE encontra a medida de similaridade entre pares de instâncias em um espaço dimensional superior e inferior. Depois disso, ele tenta otimizar duas medidas de similaridade. Ele faz tudo isso em três etapas. 

1. O t-SNE modela um ponto que está sendo selecionado como vizinho de outro ponto em dimensões superiores e inferiores. Ele começa calculando uma similaridade de pares entre todos os pontos de dados no espaço de alta dimensão usando um kernel gaussiano. Os pontos distantes entre si têm uma probabilidade menor de serem escolhidos do que os pontos próximos entre si. 
2. Em seguida, o algoritmo tenta mapear pontos de dados de maior dimensão em um espaço de menor dimensão, preservando as semelhanças entre pares. 
3. Isso é obtido minimizando a divergência entre a distribuição de probabilidade da dimensão alta original e da dimensão baixa. O algoritmo usa a descida do gradiente para minimizar a divergência. A incorporação de dimensão inferior é otimizada para um estado estável.

O processo de otimização permite a criação de clusters e subclusters de pontos de dados semelhantes no espaço de dimensão inferior que são visualizados para entender a estrutura e o relacionamento nos dados de dimensão superior. 

Exemplo de t-SNE em Python

No exemplo em Python, geraremos dados de classificação, executaremos PCA e t-SNE e visualizaremos os resultados. Para realizar a redução de dimensionalidade, usaremos o Scikit-Learn, e para a visualização, usaremos o Plotly Express. 

Geração do conjunto de dados de classificação

Usaremos a função make_classification do Scikit-Learn para gerar dados sintéticos com 6 recursos, 1500 amostras e 3 classes. 

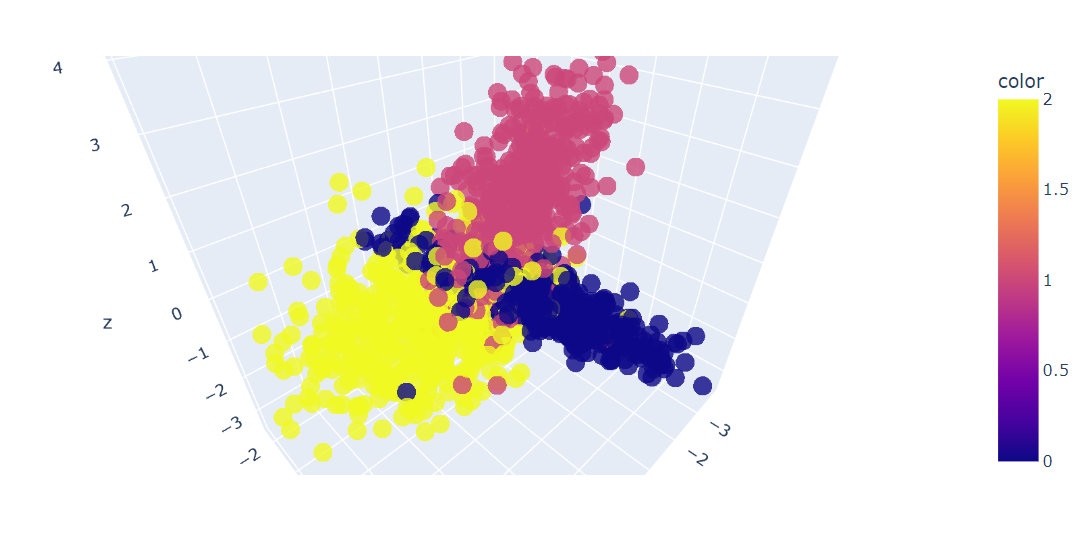
Depois disso, plotaremos em 3D os três primeiros recursos dos dados usando a função Plotly Express scatter_3d. 

import plotly.express as px
from sklearn.datasets import make_classification

X, y = make_classification(
    n_features=6,
    n_classes=3,
    n_samples=1500,
    n_informative=2,
    random_state=5,
    n_clusters_per_class=1,
)


fig = px.scatter_3d(x=X[:, 0], y=X[:, 1], z=X[:, 2], color=y, opacity=0.8)
fig.show()

Temos um gráfico 3D dos dados; você também pode visualizar os dados em um gráfico 2D usando a função Plotly Express scatter.

Ajuste e transformação de PCA

Agora, aplicaremos o algoritmo PCA no conjunto de dados para retornar dois componentes PCA. O fit_transform aprende e transforma o conjunto de dados ao mesmo tempo.  

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

t-SNE Visualization Python

Agora podemos visualizar os resultados exibindo dois componentes de PCA em um gráfico de dispersão. 

• x: Primeiro componente
• y: Segundo acompanhante
• cor: variável de destino.

Também usamos a função update_layout para adicionar um título e renomear o eixo x e o eixo y.

fig = px.scatter(x=X_pca[:, 0], y=X_pca[:, 1], color=y)
fig.update_layout(
    title="PCA visualization of Custom Classification dataset",
    xaxis_title="First Principal Component",
    yaxis_title="Second Principal Component",
)
fig.show()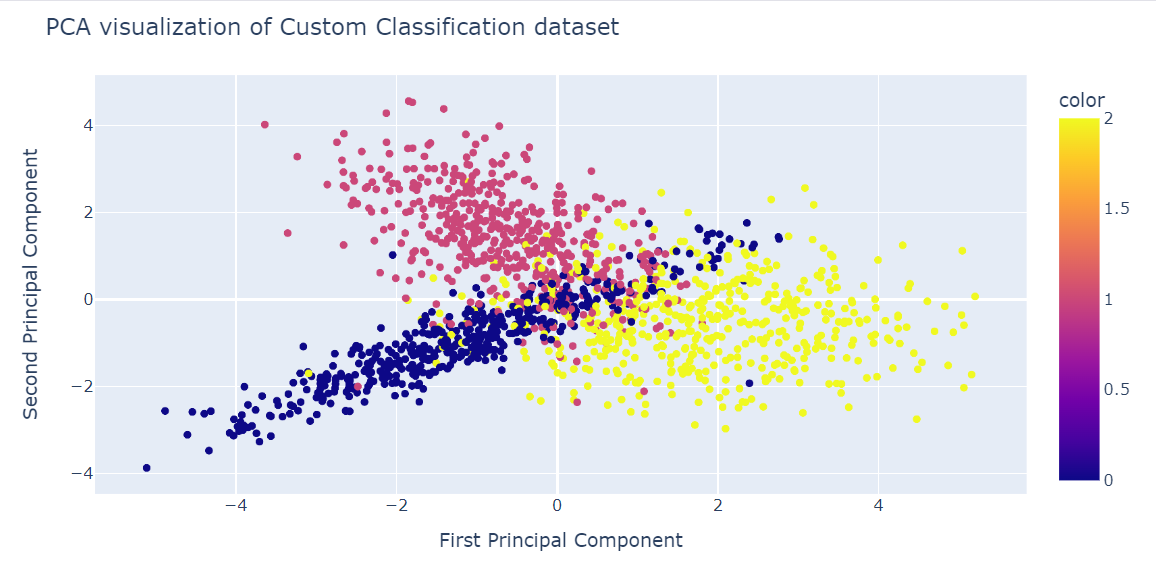

Ajuste e transformação de t-SNE

Agora, aplicaremos o algoritmo t-SNE ao conjunto de dados e compararemos os resultados. 

Após o ajuste e a transformação dos dados, exibiremos a divergência de Kullback-Leibler (KL) entre a distribuição de probabilidade de alta dimensão e a distribuição de probabilidade de baixa dimensão. 

A divergência KL baixa é um sinal de melhores resultados.

from sklearn.manifold import TSNE

tsne = TSNE(n_components=2, random_state=42)
X_tsne = tsne.fit_transform(X)
tsne.kl_divergence_

1.1169137954711914

t-SNE Visualization Python

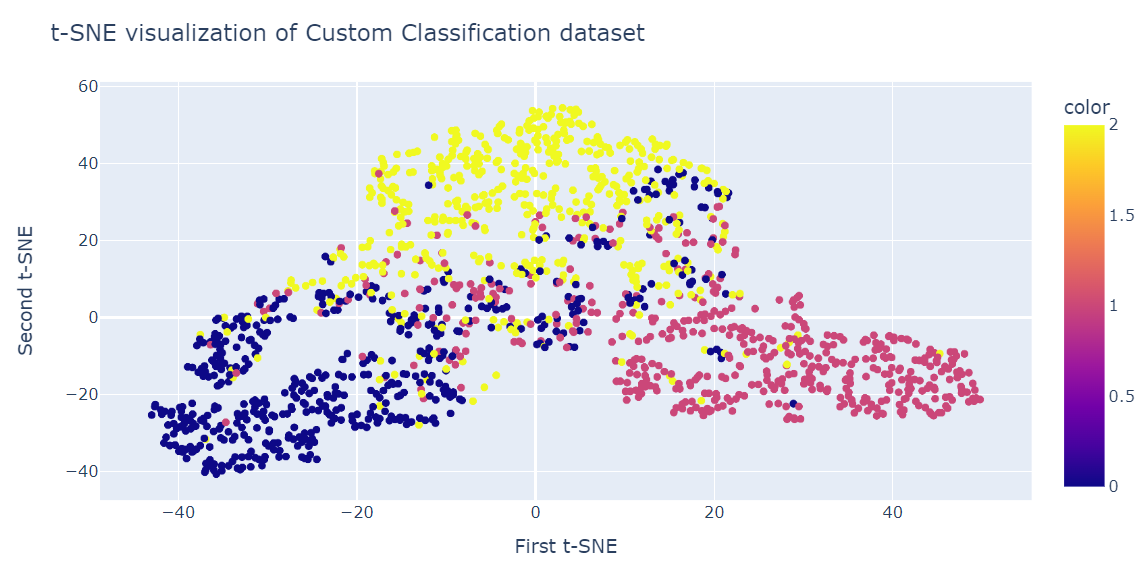
De forma semelhante à PCA, visualizaremos dois componentes t-SNE em um gráfico de dispersão. 

fig = px.scatter(x=X_tsne[:, 0], y=X_tsne[:, 1], color=y)
fig.update_layout(
    title="t-SNE visualization of Custom Classification dataset",
    xaxis_title="First t-SNE",
    yaxis_title="Second t-SNE",
)
fig.show()

O resultado é muito melhor do que o PCA. Podemos ver claramente três grandes grupos. 

t-SNE no conjunto de dados de rotatividade de clientes

Nesta seção, usaremos o conjunto de dados real de rotatividade de clientes de uma empresa de telecomunicações iraniana. O conjunto de dados contém informações sobre a atividade dos clientes, como falhas de chamadas e duração da assinatura, e um rótulo de rotatividade.

Churn significa a porcentagem de clientes que deixam de usar um determinado serviço em um determinado período de tempo.

Observação: O código-fonte e o conjunto de dados de ambos os exemplos estão disponíveis no DataCamp Workspace.

Importação do conjunto de dados de rotatividade de clientes

Carregaremos o conjunto de dados usando o pandas e exibiremos as três primeiras linhas.

import pandas as pd

df = pd.read_csv("data/customer_churn.csv")
df.head(3)

Redução de dimensionalidade PCA

Depois disso, nós o faremos:

• Crie recursos (X) e alvos (y) usando a coluna Churn.
• Normalize os recursos usando um dimensionador padrão.
• Divida o conjunto de dados em um conjunto de treinamento e outro de teste.
• Aplique PCA ao conjunto de dados de treinamento.
• Obtenha a pontuação usando o conjunto de dados de teste. A pontuação representa a probabilidade logarítmica média de todas as amostras.

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

X = df.drop('Churn', axis=1)
y = df['Churn']

scaler = StandardScaler()
X_norm = scaler.fit_transform(X)

X_train, X_test, y_train, y_test = train_test_split(
    X_norm, y, random_state=13, test_size=0.25, shuffle=True
)

pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train)

pca.score(X_test)

-17.04482851288105

Visualização de PCA

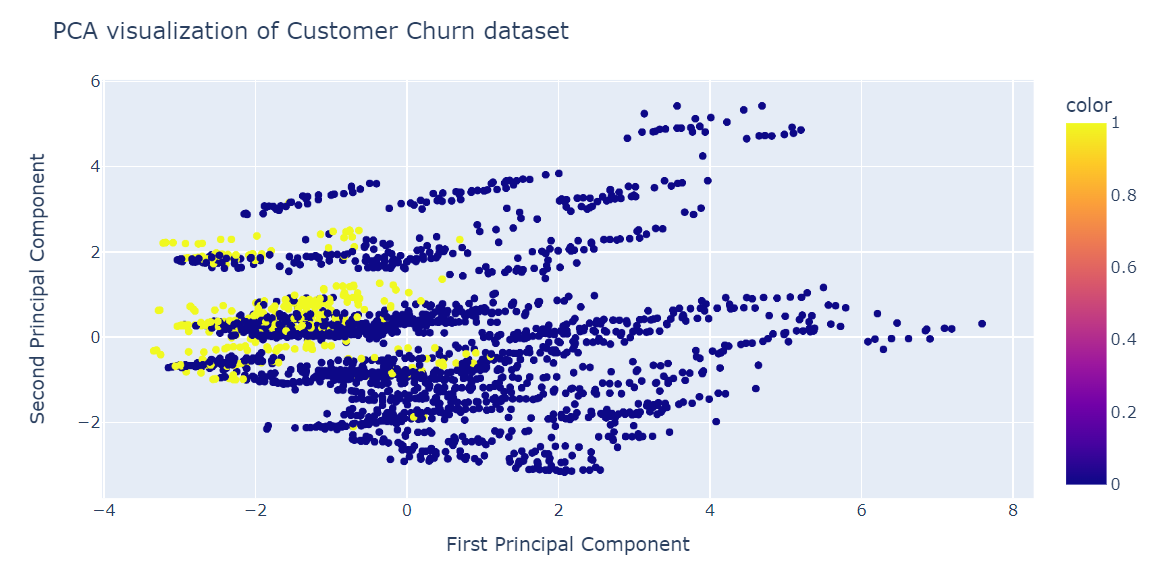
Agora visualizaremos o resultado do PCA usando o gráfico de dispersão do Plotly Express. 

fig = px.scatter(x=X_train_pca[:, 0], y=X_train_pca[:, 1], color=y_train)
fig.update_layout(
    title="PCA visualization of Customer Churn dataset",
    xaxis_title="First Principal Component",
    yaxis_title="Second Principal Component",
)
fig.show()

A PCA não foi boa na criação de agrupamentos. Os dados na dimensão baixa parecem aleatórios. Isso também pode significar que os recursos do conjunto de dados são altamente distorcidos ou que ele não tem uma estrutura de correlação forte. 

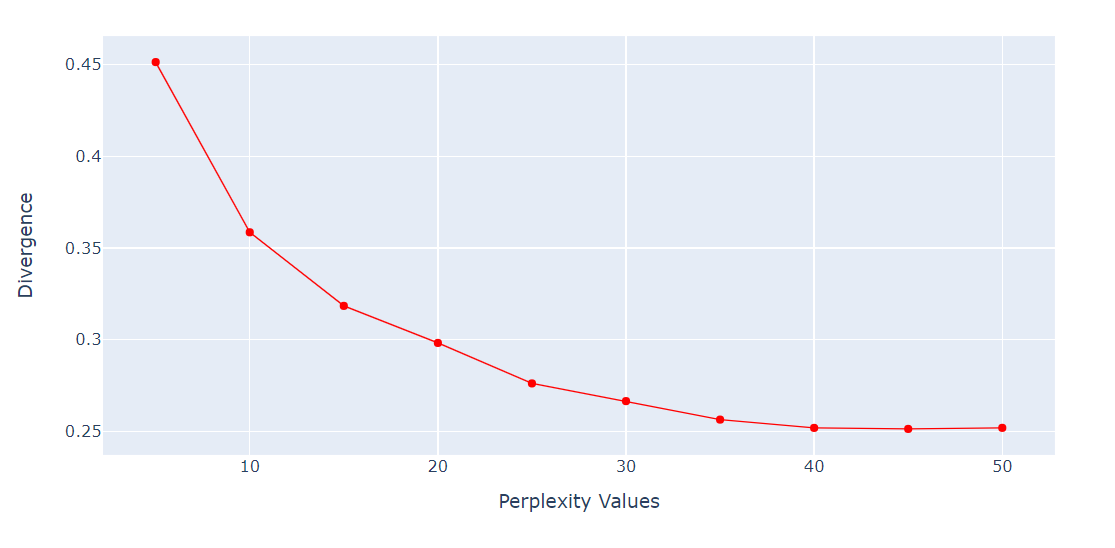
Verificação da perplexidade vs. Divergência

Para o algoritmo t-SNE, a perplexidade é um hiperparâmetro muito importante. Ele controla o número efetivo de vizinhos que cada ponto considera durante o processo de redução de dimensionalidade. 

Executaremos um loop para obter a métrica KL Divergence em várias perplexidades de 5 a 55 com intervalo de 5 pontos. Depois disso, exibiremos o resultado usando o gráfico de linhas do Plotly Express.

import numpy as np

perplexity = np.arange(5, 55, 5)
divergence = []

for i in perplexity:
    model = TSNE(n_components=2, init="pca", perplexity=i)
    reduced = model.fit_transform(X_train)
    divergence.append(model.kl_divergence_)
fig = px.line(x=perplexity, y=divergence, markers=True)
fig.update_layout(xaxis_title="Perplexity Values", yaxis_title="Divergence")
fig.update_traces(line_color="red", line_width=1)
fig.show()

A Divergência KL tornou-se constante após 40 perplexidades. Portanto, usaremos 40 de perplexidade no algoritmo t-SNE.  

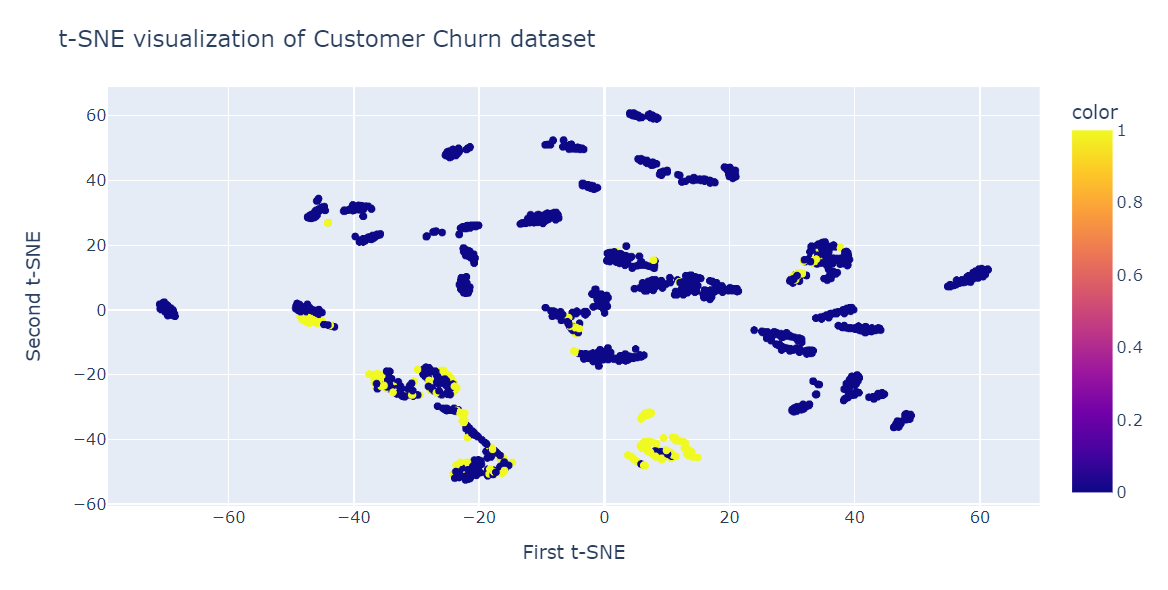
Redução de dimensionalidade t-SNE

Agora, ajustaremos o t-SNE e transformaremos os dados em dimensões menores usando 40 perplexidades para obter a menor divergência KL. 

from sklearn.manifold import TSNE

tsne = TSNE(n_components=2,perplexity=40, random_state=42)
X_train_tsne = tsne.fit_transform(X_train)

tsne.kl_divergence_

0.258713960647583

Visualização do t-SNE

Agora, usaremos o gráfico de dispersão do Plotly para exibir componentes e classes de destino. 

fig = px.scatter(x=X_train_tsne[:, 0], y=X_train_tsne[:, 1], color=y_train)
fig.update_layout(
    title="t-SNE visualization of Customer Churn dataset",
    xaxis_title="First t-SNE",
    yaxis_title="Second t-SNE",
)
fig.show()

Como podemos ver, temos vários clusters e subclusters. Podemos usar essas informações para entender o padrão e elaborar uma estratégia para reter os clientes existentes. 

Aplicação do t-SNE

Além de visualizar dados multidimensionais complexos, o t-SNE tem outros usos, principalmente na área médica. 

1. Agrupamento e classificação: para agrupar pontos de dados semelhantes em um espaço de dimensão inferior. Ele também pode ser usado para classificar e encontrar padrões nos dados. 
2. Detecção de anomalias: para identificar outliers e anomalias nos dados. 
3. Processamento de linguagem natural: para visualizar a incorporação de palavras gerada a partir de um grande corpus de texto que facilita a identificação de semelhanças e relacionamentos entre palavras.
4. Segurança de computadores: para visualizar padrões de tráfego de rede e detectar anomalias.
5. Pesquisa sobre câncer: para visualizar perfis moleculares de amostras de tumores e identificar subtipos de câncer. 
6. Interpretação do domínio geológico: para visualizar atributos sísmicos e identificar anomalias geológicas. 
7. Processamento de sinais biomédicos: para visualizar o eletroencefalograma (EEG) e detectar padrões de atividade cerebral. 

Conclusão

O t-SNE é uma poderosa ferramenta de visualização para revelar padrões e estruturas ocultas em conjuntos de dados complexos. Você pode usá-lo para imagens, áudio, dados biológicos e dados individuais para identificar anomalias e padrões. 

Nesta postagem do blog, aprendemos sobre o t-SNE, uma técnica popular de redução de dimensionalidade que pode visualizar dados não lineares de alta dimensão em um espaço de baixa dimensão. Explicamos a ideia principal por trás do t-SNE, como ele funciona e suas aplicações. Além disso, mostramos alguns exemplos de aplicação do t-SNE a conjuntos de dados sintéticos e reais e como interpretar os resultados. 

O t-SNE faz parte do aprendizado não supervisionado, e a próxima etapa natural é entender o agrupamento hierárquico, o PCA, a descorrelação e a descoberta de recursos interpretáveis. Aprenda todos os tópicos fazendo nosso curso Aprendizado não supervisionado em Python.