¿Qué es una regresión lineal?
Una regresión lineal es un modelo estadístico que analiza la relación entre una variable de respuesta (a menudo llamada y) y una o más variables y sus interacciones (a menudo llamadas x o variables explicativas). Haces este tipo de relación en tu cabeza todo el tiempo, por ejemplo, cuando calculas la edad de un niño basándote en su altura, estás suponiendo que cuanto mayor sea, más alto será.
La regresión lineal es uno de los modelos estadísticos más básicos que existen, sus resultados pueden ser interpretados por casi todo el mundo, y existe desde el siglo XIX. Esto es precisamente lo que hace que la regresión lineal sea tan popular. Es sencillo y ha sobrevivido durante cientos de años. Aunque no es tan sofisticado como otros algoritmos como las redes neuronales artificiales o los bosques aleatorios, según una encuesta realizada por KD Nuggets, la regresión fue el algoritmo más utilizado por los científicos de datos en 2016 y 2017. ¡Incluso se predice que se seguirá utilizando en el año 2118!
En este tutorial de regresión lineal, exploraremos cómo crear una regresión lineal en R, viendo los pasos que tendrás que dar con un ejemplo con el que podrás trabajar.
Practica la regresión lineal en R con este ejercicio práctico.
Crear una regresión lineal en R
No todos los problemas pueden resolverse con el mismo algoritmo. En este caso, la regresión lineal supone que existe una relación lineal entre la variable de respuesta y las variables explicativas. Esto significa que puedes ajustar una recta entre las dos (o más variables). En el ejemplo anterior de la edad del niño, está claro que existe una relación entre la edad de los niños y su estatura.
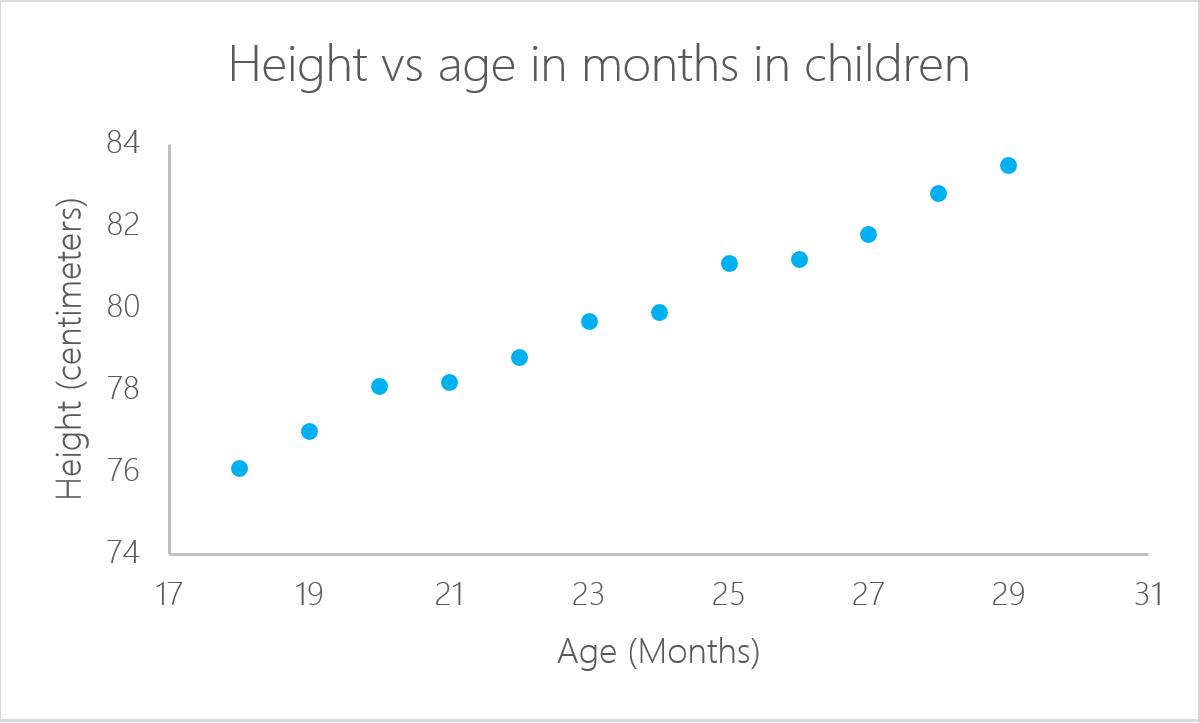
En este ejemplo concreto, puedes calcular la altura de un niño si conoces su edad:
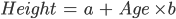
En este caso, "a" y "b" se llaman intercepto y pendiente, respectivamente. Con el mismo ejemplo, "a" o el intercepto, es el valor a partir del cual empiezas a medir. Los recién nacidos con cero meses no miden necesariamente cero centímetros; ésta es la función del intercepto. La pendiente mide el cambio de altura con respecto a la edad en meses. En general, por cada mes que tenga el niño, su estatura aumentará con "b".
lm en R
Se puede calcular una regresión lineal en R con el comando lm. En el siguiente ejemplo, utiliza este comando para calcular la altura en función de la edad del niño.
Primero, importa la biblioteca readxl para leer archivos de Microsoft Excel, puede ser cualquier tipo de formato, siempre que R pueda leerlo. Para saber más sobre la importación de datos a R, puedes seguir este curso de DataCamp.
Puedes descargar los datos que utilizarás en este tutorial antes de empezar. Descarga los datos en un objeto llamado ageandheight y luego crea la regresión lineal en la tercera línea.
función lm en R:
En lm toma las variables en el formato
lm([target] ~ [predictor / features], data = [data source])
Con el comando summary(lmHeight) puedes ver información detallada sobre el rendimiento y los coeficientes del modelo.
library(readxl)
ageandheight <- read_excel("ageandheight.xls", sheet = "Hoja2") #Upload the data
lmHeight = lm(height~age, data = ageandheight) #Create the linear regression
summary(lmHeight) #Review the resultsEmpieza a aprender R gratis
Intermediate Regression in R
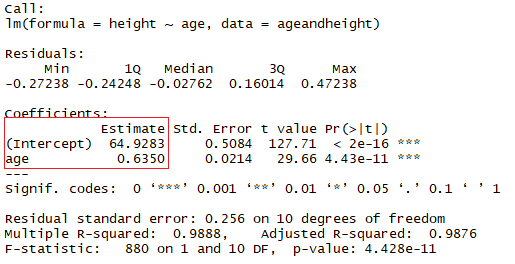
Coeficientes
En el cuadrado rojo, puedes ver los valores de la intercepción (valor "a") y la pendiente (valor "b") para la edad. Estos valores "a" y "b" trazan una línea entre todos los puntos de los datos. Así, en este caso, si hay un niño de 20,5 meses, a es 64,92 y b es 0,635, el modelo predice (de media) que su altura en centímetros es de unos 64,92 + (0,635 * 20,5) = 77,93 cm.
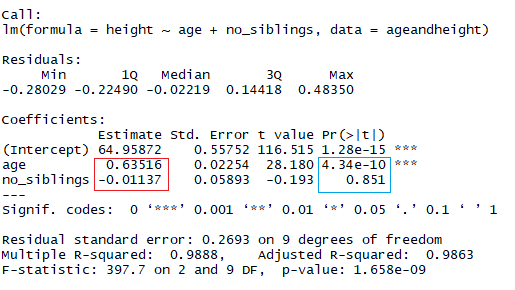
Cuando una regresión tiene en cuenta dos o más predictores para crear la regresión lineal, se llama regresión lineal múltiple. Por la misma lógica que utilizaste en el ejemplo sencillo anterior, la altura del niño se medirá por:
Altura = a + Edad × b1 + (Número de hermanos} × b2
Ahora estás viendo la altura en función de la edad en meses y del número de hermanos que tiene el niño. En la imagen anterior, el rectángulo rojo indica los coeficientes (b1 y b2). Puedes interpretar estos coeficientes de la siguiente manera:
Al comparar niños con el mismo número de hermanos, la estatura media prevista aumenta en 0,63 cm por cada mes que tiene el niño. Del mismo modo, al comparar niños de la misma edad, la estatura disminuye (porque el coeficiente es negativo) en -0,01 cm por cada aumento del número de hermanos.
En R, para añadir otro coeficiente, añade el símbolo "+" por cada variable adicional que quieras añadir al modelo.
lmHeight2 = lm(height~age + no_siblings, data = ageandheight) #Create a linear regression with two variables
summary(lmHeight2) #Review the resultsComo ya te habrás dado cuenta, fijarse en el número de hermanos es una forma tonta de predecir la estatura de un niño. Otro aspecto al que debes prestar atención en tus modelos lineales es el valor p de los coeficientes. En el ejemplo anterior, el rectángulo azul indica los valores p de los coeficientes edad y número de hermanos. En términos sencillos, un valor p indica si puedes rechazar o aceptar una hipótesis. La hipótesis, en este caso, es que el predictor no es significativo para tu modelo.
- El valor p para la edad es 4,34*e-10 o 0,000000000434. Un valor muy pequeño significa que la edad es probablemente un complemento excelente para tu modelo.
- El valor p para el número de hermanos es 0,85. En otras palabras, hay un 85% de posibilidades de que este predictor no sea significativo para la regresión.
Una forma estándar de comprobar si los predictores no son significativos es observar si los valores p son inferiores a 0,05.
Residuos
Una buena forma de comprobar la calidad del ajuste del modelo es observar los residuos o las diferencias entre los valores reales y los valores predichos. La línea recta de la imagen anterior representa los valores previstos. La línea vertical roja desde la recta hasta el valor de los datos observados es el residuo.
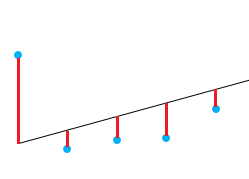
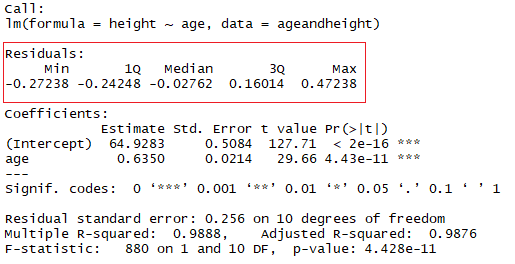
La idea es que la suma de los residuos sea aproximadamente cero o lo más baja posible. En la vida real, la mayoría de los casos no seguirán una línea perfectamente recta, por lo que se esperan residuos. En el resumen en R de la función lm, puedes ver estadísticas descriptivas sobre los residuos del modelo, siguiendo el mismo ejemplo, el cuadrado rojo muestra cómo los residuos son aproximadamente cero.
Cómo comprobar si tu modelo lineal tiene un buen ajuste
Una medida muy utilizada para comprobar lo bueno que es tu modelo es el coeficiente de determinación o R². Esta medida se define por la proporción de la variabilidad total explicada por el modelo de regresión.
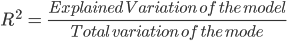
Esto puede parecer un poco complicado, pero en general, para los modelos que se ajustan bien a los datos, R² se aproxima a 1. Los modelos que se ajustan mal a los datos tienen un R² cercano a 0. En los ejemplos siguientes, el primero tiene un R² de 0,02; esto significa que el modelo sólo explica el 2% de la variabilidad de los datos. El segundo tiene un R² de 0,99, y el modelo puede explicar el 99% de la variabilidad total.**
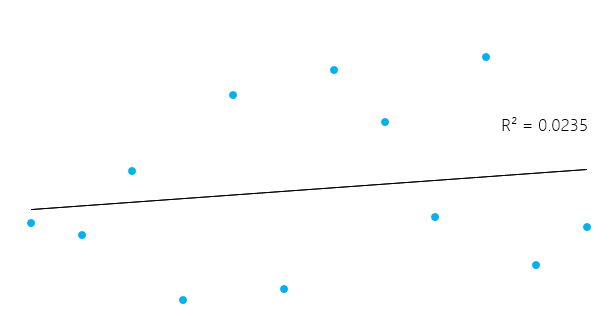
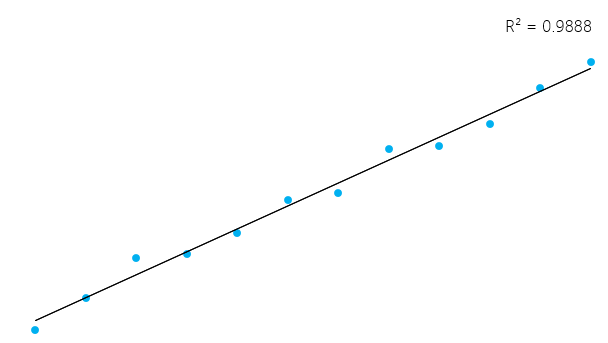
Sin embargo, es esencial tener en cuenta que, a veces, un R² alto no es necesariamente bueno siempre (véanse los gráficos residuales más abajo) y un R² bajo no es necesariamente siempre malo. En la vida real, los acontecimientos no encajan siempre en una línea perfectamente recta. Por ejemplo, puedes tener en tus datos niños más altos o más pequeños con la misma edad. En algunos campos, un R² de 0,5 se considera bueno.
Con el mismo ejemplo anterior, mira el resumen del modelo lineal para ver su R².
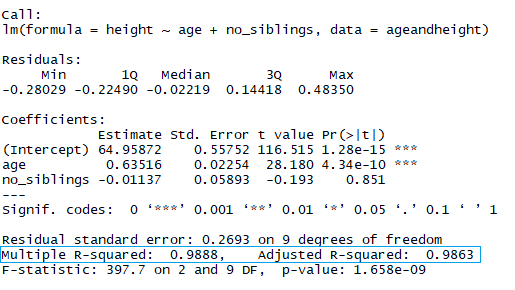
En el rectángulo azul, observa que hay dos R² diferentes, una múltiple y otra ajustada. El múltiplo es el R² que has visto anteriormente. Un problema de este R² es que no puede disminuir a medida que añades más variables independientes a tu modelo, seguirá aumentando a medida que hagas el modelo más complejo, aunque estas variables no añadan nada a tus predicciones (como el ejemplo del número de hermanos). Por esta razón, probablemente sea mejor fijarse en la R² ajustada si añades más de una variable al modelo, ya que sólo aumenta si reduce el error global de las predicciones.
¡No te olvides de mirar los residuos!
Puedes tener un R² bastante bueno en tu modelo, pero no nos apresuremos a sacar conclusiones. Veamos un ejemplo. Vas a predecir la presión de un material en un laboratorio en función de su temperatura.
Vamos a trazar los datos (en un simple diagrama de dispersión) y añadir la línea que construiste con tu modelo lineal. En este ejemplo, deja que R lea primero los datos, de nuevo con la función read_excel para crear un marco de datos con los datos, y luego crea una regresión lineal con tus nuevos datos. La orden plot toma un marco de datos y traza las variables en él. En este caso, traza la presión frente a la temperatura del material. A continuación, añade la línea obtenida por la regresión lineal con el comando abline.
pressure <- read_excel("pressure.xlsx") #Upload the data
lmTemp = lm(Pressure~Temperature, data = pressure) #Create the linear regression
plot(pressure, pch = 16, col = "blue") #Plot the results
abline(lmTemp) #Add a regression line
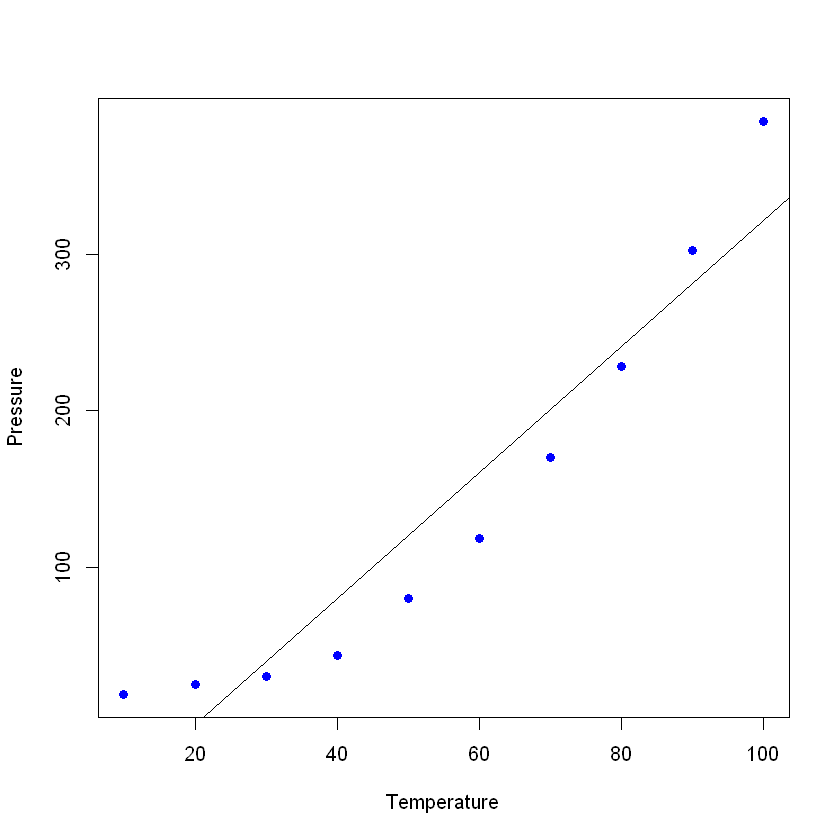
Si ves el resumen de tu nuevo modelo, podrás comprobar que tiene unos resultados bastante buenos (mira la R²y la R² ajustada)
summary(lmTemp)
Call:
lm(formula = Pressure ~ Temperature, data = pressure)
Residuals:
Min 1Q Median 3Q Max
-41.85 -34.72 -10.90 24.69 63.51
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -81.5000 29.1395 -2.797 0.0233 *
Temperature 4.0309 0.4696 8.583 2.62e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 42.66 on 8 degrees of freedom
Multiple R-squared: 0.902, Adjusted R-squared: 0.8898
F-statistic: 73.67 on 1 and 8 DF, p-value: 2.622e-05Lo ideal sería que, al trazar los residuos, tuvieran un aspecto aleatorio. Lo contrario significa que tal vez haya un patrón oculto que el modelo lineal no está considerando. Para representar gráficamente los residuos, utiliza el comando plot(lmTemp$residuals).
plot(lmTemp$residuals, pch = 16, col = "red")
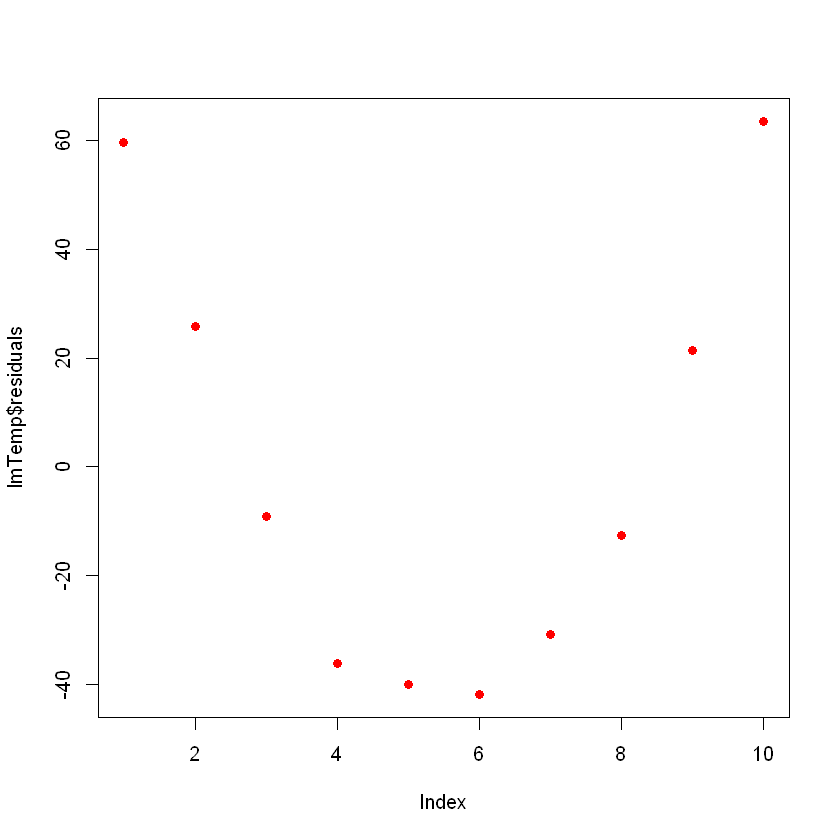
Esto puede ser un problema. Si tienes más datos, tu modelo lineal simple no podrá generalizar bien. En la imagen anterior, observa que hay un patrón (como una curva en los residuos). Esto no es aleatorio en absoluto.
Lo que puedes hacer es una transformación de la variable. Se pueden realizar muchas transformaciones posibles en tus datos, como añadir un término cuadrático (x 2), uno cúbico (x3), o incluso más complejos como ln(X), ln(X+1), sqrt(X), 1/x, Exp(X). La elección de la transformación correcta se conseguirá con cierto conocimiento de las funciones algebraicas, práctica, ensayo y error.
Probemos con un término cuadrático. Para ello, añade el término "I" (mayúscula) antes de tu transformación; por ejemplo, ésta será la fórmula de regresión lineal normal:
lmTemp2 = lm(Pressure~Temperature + I(Temperature^2), data = pressure) #Create a linear regression with a quadratic coefficient
summary(lmTemp2) #Review the results
Call:
lm(formula = Pressure ~ Temperature + I(Temperature^2), data = pressure)
Residuals:
Min 1Q Median 3Q Max
-4.6045 -1.6330 0.5545 1.1795 4.8273
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 33.750000 3.615591 9.335 3.36e-05 ***
Temperature -1.731591 0.151002 -11.467 8.62e-06 ***
I(Temperature^2) 0.052386 0.001338 39.158 1.84e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.074 on 7 degrees of freedom
Multiple R-squared: 0.9996, Adjusted R-squared: 0.9994
F-statistic: 7859 on 2 and 7 DF, p-value: 1.861e-12Observa que el modelo mejoró significativamente. Si trazas los residuos del nuevo modelo, tendrán este aspecto:
plot(lmTemp2$residuals, pch = 16, col = "red")
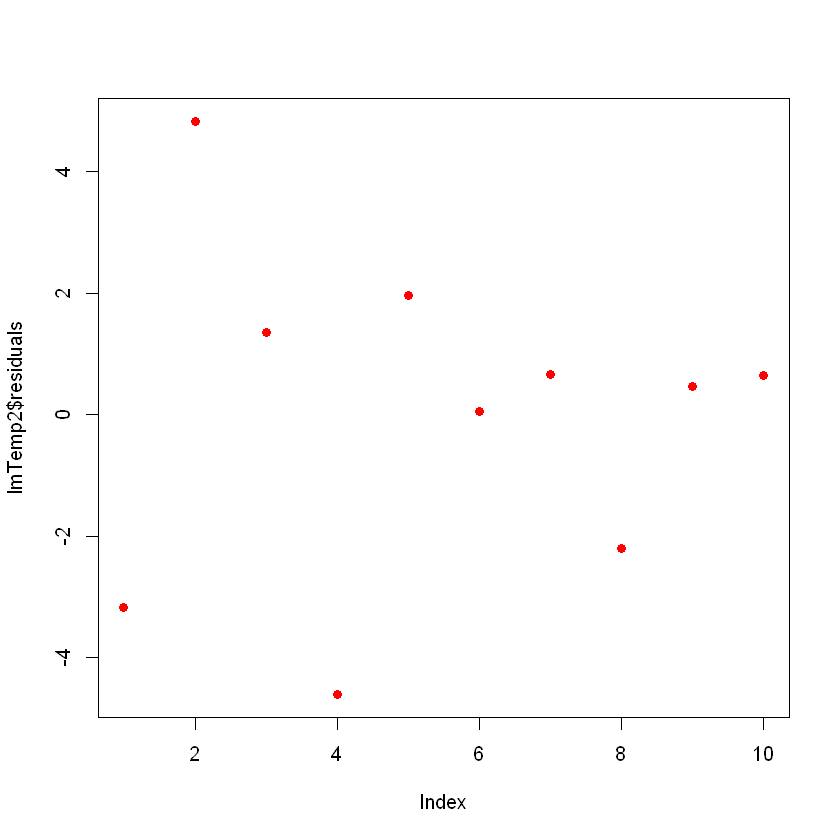
Ahora no ves ningún patrón claro en tus residuos, ¡lo cual es bueno!
Detectar puntos influyentes
En tus datos, puedes tener puntos influyentes que podrían sesgar tu modelo, a veces innecesariamente. Piensa en un error en la introducción de datos, y en lugar de escribir "2,3" el valor era "23". El tipo más común de punto influyente son los valores atípicos, que son puntos de datos en los que la respuesta observada no parece seguir el patrón establecido por el resto de los datos.
Puedes detectar puntos influyentes observando el objeto que contiene el modelo lineal, utilizando la función cooks.distance y luego traza estas distancias. Cambia un valor a propósito para ver cómo queda en el gráfico Distancia Cooks. Para cambiar un valor concreto, puedes señalarlo directamente con ageandheight[row number, column number] = [new value]. En este caso, la altura se cambia a 7,7 del segundo ejemplo:
ageandheight[2, 2] = 7.7
head(ageandheight)
| edad | altura | no_siblings |
|---|---|---|
| 18 | 76.1 | 0 |
| 19 | 7.7 | 2 |
| 20 | 78.1 | 0 |
| 21 | 78.2 | 3 |
| 22 | 78.8 | 4 |
| 23 | 79.7 | 1 |
Vuelve a crear el modelo y comprueba cómo el resumen está dando un mal ajuste, y luego traza las Distancias Cooks. Para ello, después de crear la regresión lineal, utiliza el comando cooks.distance([linear model] y luego, si quieres, puedes trazar estas distancias con el comando plot.
lmHeight3 = lm(height~age, data = ageandheight)#Create the linear regression
summary(lmHeight3)#Review the results
plot(cooks.distance(lmHeight3), pch = 16, col = "blue") #Plot the Cooks Distances.
Call:
lm(formula = height ~ age, data = ageandheight)
Residuals:
Min 1Q Median 3Q Max
-53.704 -2.584 3.609 9.503 17.512
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.905 38.319 0.206 0.841
age 2.816 1.613 1.745 0.112
Residual standard error: 19.29 on 10 degrees of freedom
Multiple R-squared: 0.2335, Adjusted R-squared: 0.1568
F-statistic: 3.046 on 1 and 10 DF, p-value: 0.1115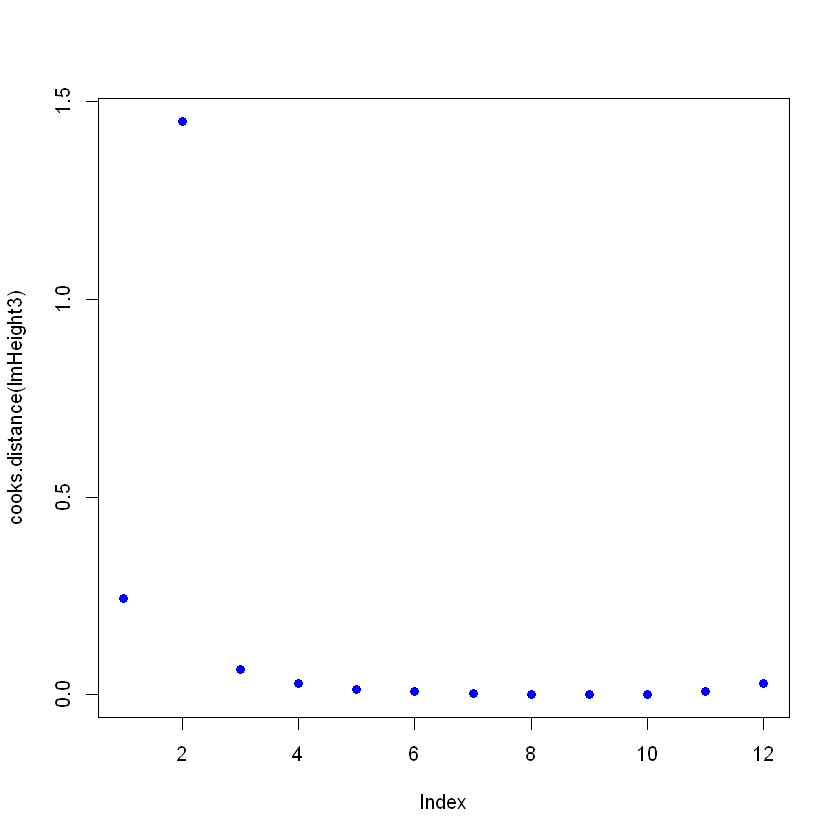
Observa que hay un punto que no sigue el patrón, y puede estar afectando al modelo. Aquí puedes tomar decisiones sobre este punto, en general, hay tres razones por las que un punto es tan influyente:
- Alguien ha cometido un error de grabación
- Alguien cometió un error fundamental al recoger la observación
- El punto de datos es perfectamente válido, en cuyo caso el modelo no puede explicar el comportamiento.
Si el caso es 1 ó 2, entonces puedes eliminar el punto (o corregirlo). Si es 3, no merece la pena eliminar un punto válido; tal vez puedas probar con un modelo no lineal en lugar de un modelo lineal como la regresión lineal.
Ten cuidado porque un punto influyente puede ser un punto válido, asegúrate de comprobar los datos y su fuente antes de eliminarlo. Es habitual ver en los libros de estadística esta cita: "A veces desechamos datos perfectamente buenos cuando deberíamos desechar modelos cuestionables".
Conclusión
¡Has llegado hasta el final! La regresión lineal es un gran tema, y ha llegado para quedarse. Aquí te presentamos algunos trucos que pueden ayudarte a afinar y sacar el máximo partido de un algoritmo tan potente y a la vez tan sencillo. También aprendiste a entender qué hay detrás de este sencillo modelo estadístico y cómo puedes modificarlo según tus necesidades. También puedes explorar otras opciones escribiendo ?lm en la consola de R y mirando los distintos parámetros que no se tratan aquí. Consulta nuestro Tutorial de Regularización : Cresta, Lazo y Red elástica. Si te interesa sumergirte en los modelos estadísticos, consulta el curso sobre Modelización Estadística en R.
Ejecuta y edita el código de este tutorial en línea
Ejecutar código