Dominar la adaptación de bajo rango (LoRA): Mejora de grandes modelos lingüísticos para una adaptación eficaz

LoRA: Adaptación de bajo rango de grandes modelos lingüísticos

El campo del aprendizaje automático y el procesamiento del lenguaje natural (PLN) ha experimentado un notable avance con la introducción de los Grandes Modelos del Lenguaje (LLM), como GPT, LLaMa, Claude 2, etc. Estos modelos han demostrado unas capacidades excepcionales en diversas aplicaciones, que van desde la generación de textos a la comprensión del lenguaje.

Sin embargo, el despliegue práctico y la puesta a punto de estos modelos conllevan importantes retos, principalmente debido a su tamaño y complejidad.

Aquí es donde entra en juego la Adaptación de Bajo Rango (LoRA), que ofrece una solución eficaz a estos retos.

El objetivo de este tutorial es lograr una comprensión teórica y práctica de qué es LoRA y cómo puedes beneficiarte de él.

Antecedentes

El inicio de la LoRA se remonta a principios de 2021, tras la publicación de la GPT-3. Microsoft, en colaboración con OpenAI, se enfrentó al reto de hacer comercialmente viables grandes modelos como el GPT-3.

Descubrieron que una sola indicación era insuficiente para lograr un rendimiento óptimo en producción, especialmente en tareas complejas como la traducción de lenguaje natural a código. Esto llevó a explorar métodos de ajuste que fueran rentables pero eficientes.

La invención de LoRA se basa en la necesidad del producto de permitir un ajuste fino rápido, eficaz y rentable de grandes modelos lingüísticos para posibilitar la especificidad de dominio, el cambio eficaz de tareas o el cambio de usuario en tiempo de ejecución.

El trabajo de investigación LoRA fue publicado en octubre de 2021 por un equipo de investigadores de Microsoft.

¿Por qué necesitamos la LoRA?

Entendamos el problema antes de entender qué es LoRa y cómo lo resuelve.

Los grandes modelos lingüísticos como GPT-4, Claude 2, LLaMA 70b, etc., son estupendos, pero son muy genéricos y grandes. Para adoptar estos grandes modelos lingüísticos para ámbitos específicos como la sanidad o la banca, o para tareas concretas como convertir texto en código, necesitamos algo que se llama ajuste fino.

El ajuste fino es el proceso de entrenar un modelo preentrenado en un conjunto de datos específico y más pequeño para especializar su rendimiento en una tarea o dominio concretos. A medida que los modelos se hacen más grandes (por ejemplo, el GPT-3 tiene 175.000 millones de parámetros), el ajuste fino completo, que vuelve a entrenar todos los parámetros del modelo, se hace menos factible debido al tiempo, el coste y los recursos.

LoRA es una técnica que se utiliza para afinar grandes modelos.

Cómo funciona la LoRA

A grandes rasgos, así es como funciona la LoRA:

Mantiene inalterado el modelo original y añade pequeñas partes modificables a cada capa del modelo. Esto reduce significativamente los parámetros entrenables del modelo y reduce los requisitos de memoria de la GPU para el proceso de entrenamiento, que es otro reto importante cuando se trata de afinar o entrenar modelos grandes.

Por ejemplo, el ajuste completo del modelo GPT-3 nos exigirá entrenar 175.000 millones de parámetros. Utilizando LoRA, los parámetros entrenables para GPT-3 se reducirán aproximadamente 10.000 veces y los requisitos de memoria de la GPU se triplicarán.

En esencia, la LoRA resuelve estos problemas:

1. Velocidad - porque menos parámetros entrenables significan un entrenamiento más rápido
2. Recursos informáticos : menos parámetros entrenables significan menos recursos informáticos necesarios para el proceso de entrenamiento, lo que hace económicamente viable afinar modelos grandes.
3. Eficacia de la memoria - menos parámetros entrenables significan que podemos almacenarlos en caché en la memoria, eliminando la necesidad de lecturas en disco, que son ineficaces comparadas con la lectura desde la memoria.

Matrices de rango inferior

Antes de entrar en los detalles de LoRA, entendamos el concepto de matrices de rango inferior.

Las matrices de rango inferior son un concepto de las matemáticas, concretamente del campo del álgebra lineal. En términos sencillos, el rango de una matriz es una medida del "contenido informativo" o la "dimensionalidad" de los datos representados por la matriz. Vamos a desglosarlo:

• Matriz:
  Una matriz es una matriz rectangular de números. Por ejemplo, una matriz de 3x3 tiene 3 filas y 3 columnas.

• Rango de una matriz
  El rango de una matriz viene determinado por el número de filas o columnas linealmente independientes de la matriz. Linealmente independiente significa que ninguna fila (o columna) puede formarse combinando otras filas (o columnas).
  Si todas las filas (o columnas) son linealmente independientes, la matriz tiene rango completo.
  Si algunas filas (o columnas) pueden formarse combinando otras filas (o columnas), la matriz tiene un rango inferior.

• Matrices de rango inferior:
  Una matriz es de rango inferior si su rango es menor que el máximo posible dado su tamaño. Por ejemplo, en una matriz de 3x3, si el rango es inferior a 3, es una matriz de rango inferior.

Ejemplo:

Considera una matriz de 3 x 3:

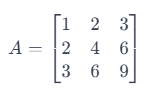
Aquí, la segunda fila es sólo la primera multiplicada por 2, y la tercera es la primera multiplicada por 3. Esto significa que las filas no son linealmente independientes. El rango de esta matriz es 1 (ya que sólo la primera fila es independiente), que es inferior al rango máximo posible para una matriz de 3x3, que es 3. Por tanto, se trata de una matriz de rango inferior.

Las matrices de rango inferior son importantes en diversas aplicaciones, como la compresión de datos, en la que reducir el rango de una matriz ayuda a comprimir los datos conservando toda la información posible.

El rango en una matriz se aplica por igual a filas y columnas. El punto crucial que hay que entender es que el rango de una matriz es el mismo tanto si lo calculas basándote en filas como en columnas. Esto se debe a una propiedad fundamental del álgebra lineal conocida como Teorema de Rank-Nulidad.

En términos más sencillos, el teorema afirma que las dimensiones del espacio de filas (espacio abarcado por las filas) y del espacio de columnas (espacio abarcado por las columnas) de una matriz son iguales. Esta dimensión común es lo que denominamos rango de la matriz.

Así, en el ejemplo anterior de la matriz de 3 x 3, el rango es 1, lo que significa que sólo hay una fila linealmente independiente y sólo una columna linealmente independiente.

¿Qué es la LoRA?

En palabras muy sencillas, LoRA aprovecha el concepto de matrices de rango inferior para que el proceso de entrenamiento del modelo sea extremadamente eficaz y rápido.

Los modelos grandes tienen muchos parámetros. Por ejemplo, GPT-3 tiene 175.000 millones de parámetros. Estos parámetros no son más que números almacenados en matrices. Almacenarlos requiere mucho espacio.

El ajuste fino completo significa que se entrenarán todos los parámetros, y esto requerirá una cantidad extraordinaria de recursos informáticos que pueden costar fácilmente millones de dólares para un modelo del tamaño de GPT.

A diferencia del ajuste fino tradicional, que requiere ajustar todo el modelo, LoRA se centra en modificar un subconjunto más pequeño de parámetros (matrices de rango inferior), reduciendo así la carga computacional y de memoria.

LoRA se basa en el entendimiento de que los grandes modelos poseen intrínsecamente una estructura de baja dimensión. Aprovechando las matrices de bajo rango, LoRA adapta eficazmente estos modelos. Este método se centra en el concepto básico de que los cambios significativos del modelo pueden representarse con menos parámetros, lo que hace que el proceso de adaptación sea más eficaz.

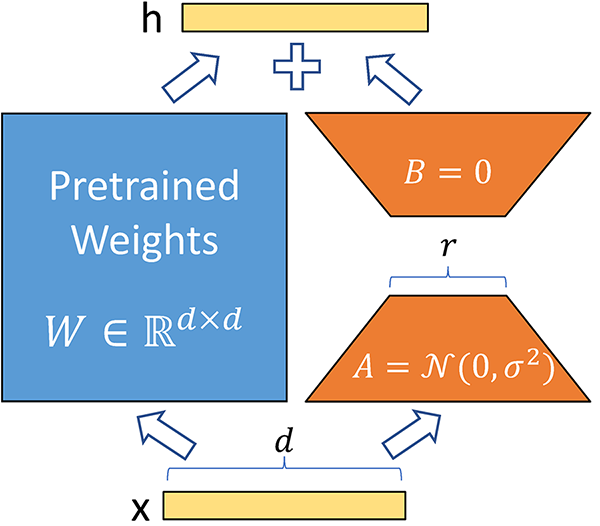
Fuente: Ajuste de los LLM: ¿LoRA o Parámetro Completo? Un análisis en profundidad con Llama 2

¿Cómo funciona?

En primer lugar, descomponemos las matrices de pesos grandes en matrices más pequeñas utilizando la técnica de la matriz de rango inferior, como se ha explicado anteriormente. Esto reduce drásticamente el número de parámetros entrenables. Para un modelo como el GPT-3, los parámetros entrenables se reducen 10000 veces. Esto significa que en lugar de entrenar 175.000 millones de parámetros, si aplicas LoRA, sólo tienes 17,5 millones de parámetros entrenables.

No cambiamos ningún parámetro de un modelo preentrenado. En su lugar, entrena sólo matrices de rango inferior, lo que ocurre relativamente muy rápido debido al menor número de parámetros.

Los pesos son aditivos. Esto significa que, para la inferencia, sólo tenemos que añadir los pesos de las matrices de rango inferior a los pesos preentrenados, sin ninguna latencia adicional. Las matrices de rango inferior también tienen un tamaño muy pequeño, por lo que es muy fácil cargarlas y descargarlas para distintas tareas y distintos usuarios.

Ventajas de la LoRA

Utilizar LoRA para el ajuste fino tiene varias ventajas:

1. Eficacia en la formación y el despliegue

LoRA reduce la carga computacional, permitiendo una adaptación más rápida de los modelos. Al requerir menos parámetros entrenables, LoRA hace factible el ajuste fino de grandes modelos en hardware menos potente.

2. Mantener la calidad y la velocidad del modelo

A pesar de la reducción del número de parámetros, LoRA mantiene la calidad y la velocidad de inferencia del modelo original.

3. Reducción del tamaño de los puntos de control

LoRA reduce drásticamente el tamaño de los puntos de control del modelo. Por ejemplo, en GPT-3, el tamaño del punto de control se redujo de 1 TB a sólo 25 MB.

4. Sin latencia de inferencia

LoRA no introduce ninguna latencia adicional durante la inferencia. Aunque se utilizan matrices de bajo rango durante el entrenamiento, se fusionan con los parámetros originales para la inferencia, lo que garantiza que no haya ralentización. Esto permite cambiar rápidamente de modelo en tiempo de ejecución sin latencia de inferencia adicional.

5. Versatilidad

La LoRA es aplicable a cualquier modelo que utilice la multiplicación de matrices (como la máquina de vectores de soporte), lo que la convierte en una técnica ampliamente aplicable en muchos otros casos de uso. De hecho, LoRA se utiliza ampliamente en los modelos de Difusión Estable para ingerir el estilo en modelos de imágenes de gran tamaño.

Difusión estable LoRA

La técnica LoRA también se adopta ampliamente en modelos de imagen como la Difusión Estable.

La idea es prácticamente la misma que la de los modelos lingüísticos. En lugar de afinar completamente grandes modelos como el de Difusión Estable, sólo entrenamos matrices de rango inferior en pequeños conjuntos de datos.

En el caso de los modelos lingüísticos, el objetivo es la especificidad de dominio. Para los modelos de imagen, el caso de uso más obvio es adoptar un estilo o un carácter coherente al generar imágenes.

Estas matrices de rango inferior se conocen como adaptadores; tienen un tamaño muy pequeño, y hay miles de ellos en Internet que puedes descargar y poner encima de tu modelo base de Difusión Estable y generar imágenes específicas para cada estilo.

Algunos usos habituales de los modelos de Difusión Estable LoRA son:

• Especialización de estilos - Estilo anime, estilo pintura al óleo, etc.
• Especialización de personajes - Genera imágenes de Mario o Bob Esponja de forma fiable
• Mejoras de calidad - Más detalles, mejores caras, etc.

Puedes combinar varias LoRA para obtener resultados que reflejen varias especializaciones.

Diferentes adaptadores para Modelos de Difusión Estable(Fuente de la imagen)

Si quieres aprender a afinar con éxito la Difusión Estable XL en fotos personales, consulta Afinar la Difusión Estable XL con DreamBooth y el blog de LoRA en Datacamp.

Combinar LoRA con Prefijo-Tuning

La sintonización de prefijos es un método ligero en el que se optimizan vectores continuos llamados "prefijos'' y se añaden a la entrada de cada capa Transformadora. El modelo se entrena de forma prefijada, centrándose sólo en estos vectores.

Ventajas de la sintonización prefija:

• Requiere almacenar sólo los pequeños vectores prefijados por tarea, en lugar de copias completas de los modelos ajustados.
• Facilita el cambio de tareas y la personalización.
• Funciona bien en comparación con el ajuste fino completo, especialmente en regímenes de datos bajos.
• Computacionalmente más barato, ya que sólo se actualizan los prefijos durante el entrenamiento.

LoRA y el ajuste de prefijos pueden combinarse dentro del marco PEFT (Ajuste Fino Eficaz de Parámetros):

• LoRA reduce los parámetros generales, mientras que el ajuste de prefijos proporciona un control específico de la tarea
• Juntos, permiten un ajuste fino especializado con un mínimo de datos y cálculo
• Muy adecuado para la adaptación al dominio de grandes LLM utilizando datos limitados en el dominio
• Este ajuste modular libera todo el potencial de los grandes LLM para los usuarios con recursos limitados.

Ejemplo de implementación de LoRA utilizando la biblioteca Loralib en Python

Para implantar LoRA, puedes utilizar la biblioteca Loralib de Microsoft. Para instalar la biblioteca:

pip install loralib

La forma en que normalmente entrenas tu red neuronal no cambia mucho para la adopción de LoRA.

# ===== Before =====
# layer = nn.Linear(in_features, out_features)

# ===== After ======
import loralib as lora
# Add a pair of low-rank adaptation matrices with rank r=16
layer = lora.Linear(in_features, out_features, r=16)

Antes de que empiece el bucle de entrenamiento, sólo tienes que añadir:

import loralib as lora

model = YourNeuralNetwork()

# This sets requires_grad to False for all parameters
lora.mark_only_lora_as_trainable(model)

# Training loop
for batch in dataloader:
   ...

Al guardar un punto de control, puedes generar un state_dic que sólo contenga parámetros LoRA.

# ===== Before =====
# torch.save(model.state_dict(), checkpoint_path)

# ===== After =====
torch.save(lora.lora_state_dict(model), checkpoint_path)

Si no entiendes bien las Redes Neuronales, no te preocupes. Consulta el blog Cómo entrenar un LLM con PyTorch para dominar el proceso de entrenamiento de grandes modelos lingüísticos utilizando PyTorch, desde la configuración inicial hasta la implementación final.

Créditos: El ejemplo de código ha sido reproducido de Microsoft/LoRA github.

Conclusión

El LoRA se perfila como una técnica indispensable para afrontar los importantes retos que plantean el tamaño y la complejidad de los grandes modelos.

Al aprovechar las matrices de rango inferior, LoRA ofrece un enfoque más eficaz y rentable para la adaptación de modelos, reduciendo significativamente los parámetros entrenables y los requisitos de memoria de la GPU, lo que permite un entrenamiento más rápido y una mayor eficiencia de la memoria.

La aplicación de LoRA se extiende más allá de los modelos lingüísticos, encontrando utilidad en modelos de imagen como la Difusión Estable, donde facilita la especialización de estilos y la coherencia de caracteres en la generación de imágenes.

Si tienes curiosidad y quieres saber más sobre lo que puedes construir con estas tecnologías, consulta nuestra guía sobre 5 proyectos que puedes construir con el blog Modelos Generativos de IA para obtener más información.