Distancia de Minkowski: Guía completa

Las métricas de distancia constituyen la columna vertebral de numerosos algoritmos de la ciencia de datos y el aprendizaje automático, ya que permiten medir la similitud o disimilitud entre puntos de datos. En esta guía exploraremos los fundamentos de la distancia de Minkowski, sus propiedades matemáticas y sus implementaciones. Examinaremos cómo se relaciona con otras medidas de distancia comunes y demostraremos su uso mediante ejemplos de codificación en Python y R. 

Tanto si desarrollas algoritmos de agrupación como si trabajas en la detección de anomalías o ajustas modelos de clasificación, comprender la distancia de Minkowski puede mejorar tu enfoque del análisis de datos y el desarrollo de modelos. Echemos un vistazo.

¿Qué es la distancia de Minkowski?

La distancia de Minkowski es una métrica versátil utilizada en espacios vectoriales normados, que debe su nombre al matemático alemán Hermann Minkowski. Es una generalización de varias medidas de distancia bien conocidas, lo que la convierte en un concepto fundamental en diversos campos, como las matemáticas, la informática y el análisis de datos.

En esencia, la distancia de Minkowski proporciona una forma de medir la distancia entre dos puntos en un espacio multidimensional. Lo que la hace especialmente útil es su capacidad para abarcar otras métricas de distancia como casos especiales, principalmente a través de un parámetro p. Este parámetro permite que la distancia de Minkowski se adapte a diferentes espacios problemáticos y características de los datos. La fórmula general de la distancia de Minkowski es:

Dónde:

• x y y son dos puntos de un espacio n-dimensional

• p es un parámetro que determina el tipo de distancia (p ≥ 1)

• |xi - yi| representa la diferencia absoluta entre las coordenadas de x e y en cada dimensión

La distancia de Minkowski es útil por dos razones principales. Por un lado, te da flexibilidad para alternar entre la distancia Manhattan o la distancia euclidiana según necesites. En segundo lugar, reconoce que no todos los conjuntos de datos (piensa en espacios de alta dimensión) se adaptan bien a la distancia puramente Manhattan o puramente euclidiana.

En la práctica, el parámetro p suele elegirse incorporando un flujo de trabajo de validación entrenamiento/prueba. Probando diferentes valores de p durante la validación cruzada, puedes determinar qué valor proporciona el mejor rendimiento del modelo para tu conjunto de datos específico.

Cómo funciona la distancia de Minkowski

Veamos cómo se relaciona la distancia de Minkowski con otras fórmulas de distancia y, a continuación, veamos un ejemplo. 

Generalización de otras métricas de distancia

Lo primero que hay que considerar es cómo la fórmula de la distancia de Minkowski contiene en su interior las fórmulas de las distancias de Manhattan, Euclidiana y de Chebyshev. 

Distancia de Manhattan (p = 1): 

Cuando p se fija en 1, la distancia de Minkowski se convierte en distancia de Manhattan. 

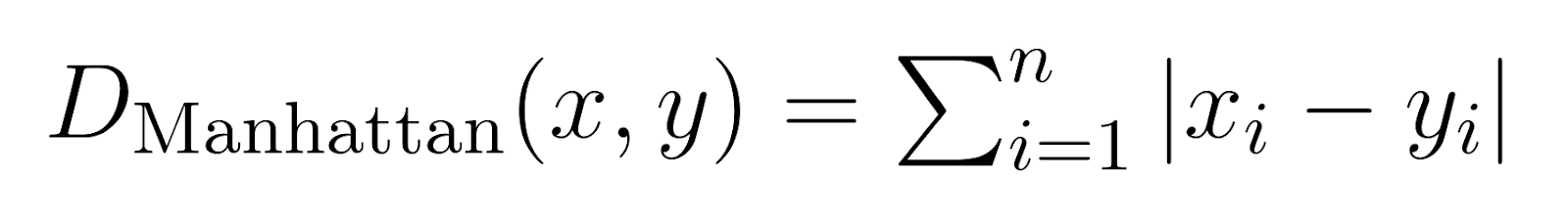
También conocida como distancia en manzanas o norma L1, la Distancia Manhattan mide la suma de las diferencias absolutas. 

Distancia euclidiana (p = 2): 

Cuando p se fija en 2, la distancia de Minkowski se convierte en distancia euclidiana.

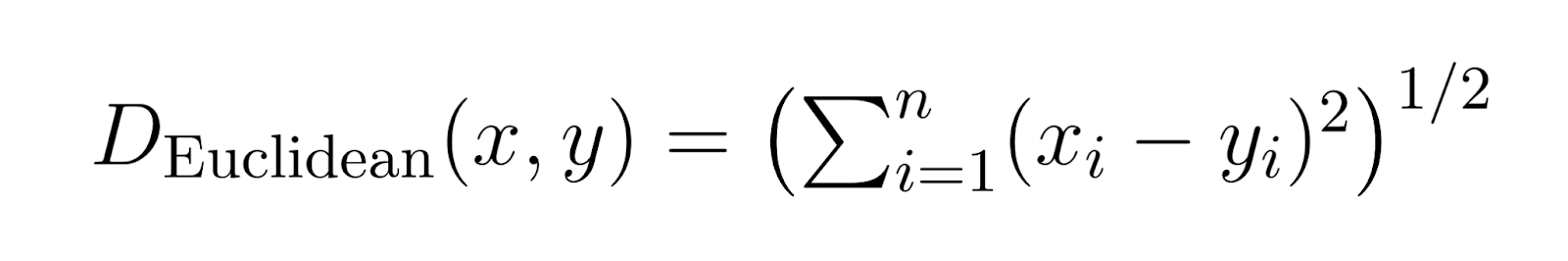
La distancia euclidiana es la métrica de distancia más común, y representa la distancia en línea recta entre dos puntos. 

Distancia de Chebyshev (p → ∞): 

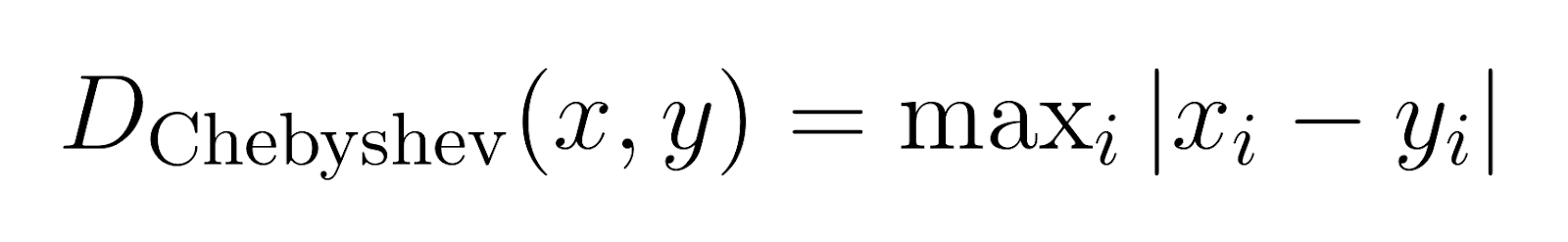
La distancia de Chebyshev, también conocida como distancia de tablero de ajedrez, mide la diferencia máxima a lo largo de cualquier dimensión. 

Trabajar con un ejemplo

Para comprender realmente la funcionalidad y la potencia de la distancia de Minkowski, veamos un ejemplo. Esta exploración nos ayudará a comprender cómo afecta el parámetro p al cálculo y la interpretación de las distancias en espacios multidimensionales.

Consideremos dos puntos en un espacio 2D:

• Punto A: (2, 3)
• Punto B: (5, 7)

Calcularemos la distancia de Minkowski entre estos puntos para distintos valores de p.

El parámetro p de la fórmula de la distancia de Minkowski controla la sensibilidad de la métrica a las diferencias en los componentes individuales:

• Cuando p=1: Todas las diferencias contribuyen linealmente.
• Cuando p=2: Las diferencias mayores tienen un impacto más significativo debido a la cuadratura.
• Cuando p>2: Se hace aún más hincapié en las grandes diferencias.
• Cuando p→∞: Sólo importa la diferencia máxima entre todas las dimensiones.

A medida que aumenta p, la distancia de Minkowski suele disminuir, acercándose a la distancia de Chebyshev. Esto se debe a que los valores más altos de p dan más peso a la mayor diferencia y menos a las diferencias más pequeñas.

Para visualizar cómo afectan los distintos valores de p al cálculo de la distancia entre nuestros puntos A(2, 3) y B(5, 7), examinemos el siguiente gráfico:

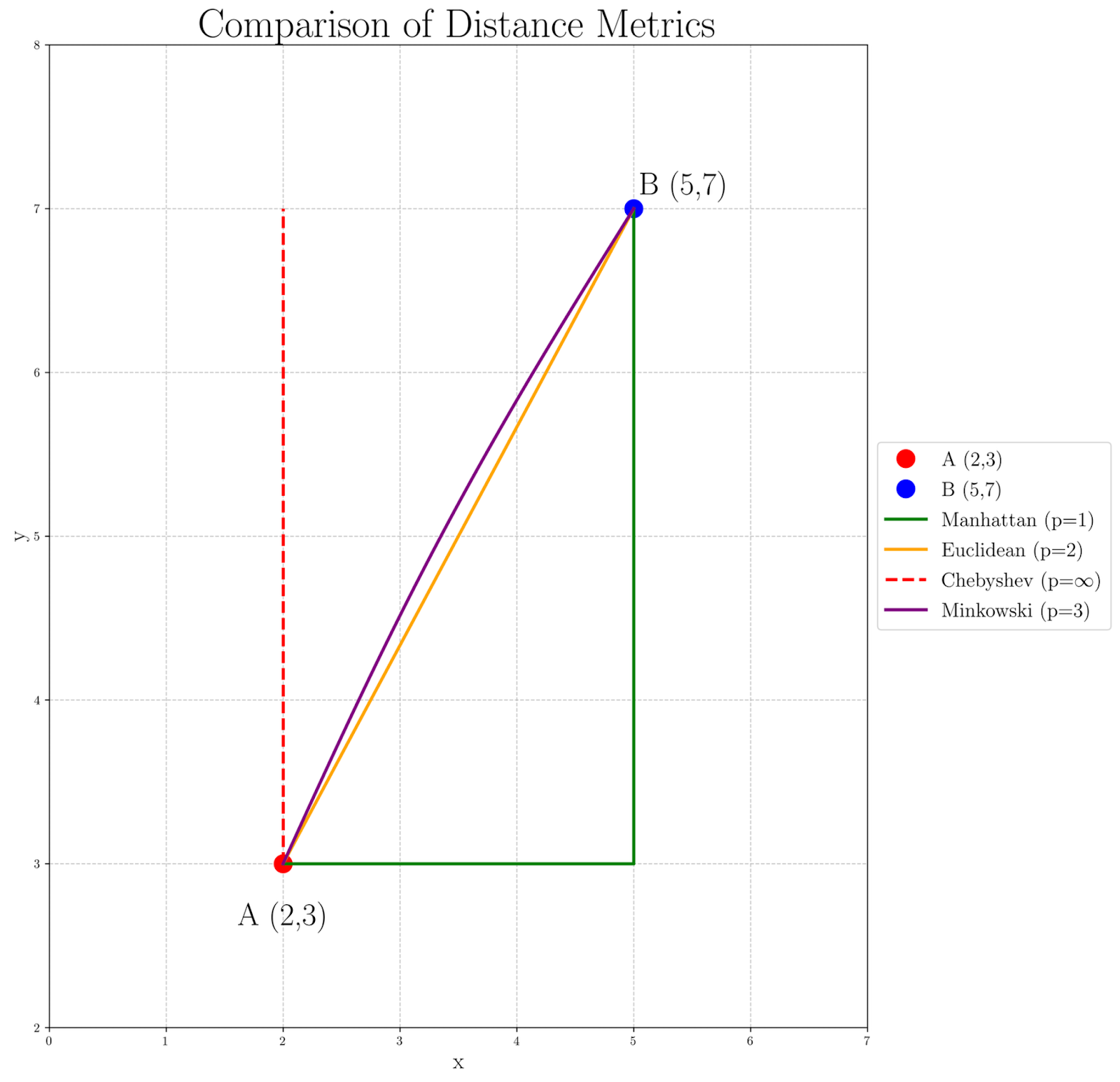
Observando el gráfico, podemos ver cómo cambia la medida de la distancia a medida que aumenta p:

• La distancia Manhattan (p=1), representada por el camino verde, produce el camino más largo, ya que sigue estrictamente la cuadrícula.
• La distancia euclidiana (p=2), mostrada por la línea recta naranja, proporciona un camino directo y rectilíneo.
• La distancia de Chebyshev (p=∞), representada por las líneas discontinuas rojas, se centra únicamente en la mayor diferencia de coordenadas, creando una trayectoria que se mueve al máximo en una dimensión antes de abordar la otra.
• La distancia de Minkowski con p=3 en púrpura muestra una ligera curva, insinuando la transición entre las distancias euclidiana y de Chebyshev.

Esta visualización nos ayuda a comprender por qué se pueden elegir distintos valores de p para diversas aplicaciones. Por ejemplo, la distancia Manhattan puede ser más apropiada en problemas de navegación urbana, mientras que la distancia euclidiana se suele utilizar en cálculos de espacio físico. Los valores más altos de p, como en el caso de Minkowski p=3, pueden ser útiles en situaciones en las que deban acentuarse las diferencias más grandes, y la distancia de Chebyshev podría preferirse cuando la diferencia máxima en cualquier dimensión sea el factor más crítico.

Aplicaciones de la distancia de Minkowski

La distancia de Minkowski, con su parámetro ajustable p, es una herramienta flexible utilizada en diversos campos. Cambiando p, podemos adaptar la forma de medir la distancia entre puntos, haciéndola adecuada para diferentes tareas. A continuación se presentan cuatro aplicaciones en las que la distancia de Minkowski desempeña un papel importante.

Aprendizaje automático y ciencia de datos

En el aprendizaje automático y la ciencia de datos, la distancia de Minkowski es fundamental para los algoritmos que se basan en medir la similitud o disimilitud entre puntos de datos. Un ejemplo destacado es el algoritmo k-Nearest Neighbors (k-NN), que clasifica los puntos de datos basándose en las categorías de sus vecinos más próximos. Al utilizar la distancia de Minkowski, podemos ajustar el parámetro p para cambiar la forma de calcular la "cercanía" entre puntos.

Reconocimiento de patrones

El reconocimiento de patrones consiste en identificar patrones y regularidades en los datos, como el reconocimiento de la escritura a mano o la detección de rasgos faciales. En este contexto, la distancia de Minkowski mide la diferencia entre vectores de características que representan patrones. Por ejemplo, en el reconocimiento de imágenes, cada imagen puede representarse mediante un vector de valores de píxeles. Calcular la distancia de Minkowski entre estos vectores nos permite cuantificar lo similares o diferentes que son las imágenes.

Ajustando p, podemos controlar la sensibilidad de la medida de distancia a las diferencias en rasgos específicos. Un p más bajo podría considerar las diferencias globales en todos los píxeles, mientras que un p más alto podría enfatizar las diferencias significativas en determinadas regiones de la imagen.

Detección de anomalías

La detección de anomalías pretende identificar puntos de datos que se desvían significativamente de la mayoría, lo que es crucial en áreas como la detección de fraudes, la seguridad de las redes y la detección de fallos en los sistemas. La distancia de Minkowski se utiliza para medir la distancia entre un punto de datos y otros del conjunto de datos. Los puntos con grandes distancias son anomalías potenciales. Eligiendo un p adecuado, los analistas pueden mejorar la sensibilidad de los sistemas de detección de anomalías a los tipos de desviaciones más relevantes para su contexto específico.

Geometría computacional y análisis espacial

En geometría computacional y análisis espacial, la distancia de Minkowski se utiliza para calcular distancias entre puntos en el espacio, lo que constituye la base de muchos algoritmos geométricos. Por ejemplo, la detección de colisiones en estos dominios se basa en la distancia de Minkowski para determinar cuándo los objetos están lo suficientemente cerca como para interactuar. Ajustando p, los desarrolladores pueden crear diversos límites de colisión, desde angulares ( p más bajo) a redondeados ( p más alto).

Más allá de la detección de colisiones, la distancia de Minkowski puede ser útil en la agrupación espacial y el análisis de formas. Variar el valor de p permite a los investigadores hacer hincapié en distintos aspectos de las relaciones espaciales, desde las distancias entre manzanas hasta las similitudes de forma general.

Propiedades matemáticas de la distancia de Minkowski

La distancia de Minkowski no sólo es una herramienta versátil en las aplicaciones prácticas, sino también un concepto importante en la teoría matemática, sobre todo en el estudio de los espacios métricos y las normas.

Propiedades del espacio métrico

La distancia de Minkowski satisface las cuatro propiedades esenciales necesarias para que una función pueda considerarse métrica en un espacio métrico:

• No negatividad: La distancia de Minkowski entre dos puntos cualesquiera es siempre no negativa, d(x,y)≥0. Esto es evidente, ya que es la raíz p-ésima de una suma de términos no negativos (valores absolutos elevados a la potencia p).
• Identidad de los Indiscernibles: La distancia de Minkowski entre dos puntos es cero si y sólo si los dos puntos son idénticos. Matemáticamente, d(x,y) = 0 si y sólo si x=y. Esto se debe a que la diferencia absoluta entre componentes idénticos es cero.
• Simetría: La distancia de Minkowski es simétrica, es decir, d(x,y)=d(y,x). Esta propiedad se mantiene porque el orden de sustracción en los términos de valor absoluto no afecta al resultado.
• Desigualdad de triángulos: La distancia de Minkowski satisface la desigualdad del triángulo, que establece que para tres puntos cualesquiera x, y y z, la distancia de x a z es como máximo la suma de la distancia de x a y y de y a z; formalmente, d(x,z)≤d(x,y)+d(y,z). Esta propiedad es menos intuitiva de demostrar directamente a partir de la fórmula y suele requerir matemáticas más avanzadas, pero esencialmente garantiza que tomar un camino directo entre dos puntos es la ruta más corta.

Generalización de normas

La distancia de Minkowski actúa como un marco general que unifica diversas formas de medir distancias en espacios matemáticos mediante el concepto de normas. En términos sencillos, unanorma es una función que asigna una longitud o tamaño no negativo a un vector en un espacio vectorial, midiendo esencialmente lo "largo" que es el vector. Ajustando el parámetro p en la fórmula de la distancia de Minkowski, podemos pasar suavemente de una norma a otra, cada una de las cuales proporciona un método único para calcular la longitud de los vectores.

Por ejemplo, cuando p=1, la distancia de Minkowski se convierte en la norma de Manhattan, que mide la distancia como la suma de las diferencias absolutas a lo largo de cada dimensión: imagina navegar por una cuadrícula de calles de la ciudad. Con p=2, se convierte en lanorma euclidiana , que calcula la distancia rectilínea ("como el canto de un gallo") entre puntos. A medida que p se acerca al infinito, converge a lanorma de Chebyshev , donde la distancia viene determinada por la mayor diferencia entre dimensiones. Esta flexibilidad permite a la distancia de Minkowski adaptarse a diversos contextos matemáticos y prácticos, lo que la convierte en una herramienta versátil para medir distancias en distintos escenarios.

Cálculo de la distancia de Minkowski en Python y R

Vamos a explorar implementaciones de cálculos de distancias de Minkowski utilizando tanto Python como R. Examinaremos paquetes y bibliotecas fácilmente disponibles que pueden lograrlo. 

Ejemplo en Python

Para calcular la distancia de Minkowski en Python, podemos utilizar la biblioteca SciPy, que proporciona implementaciones eficientes de varias métricas de distancia. Aquí tienes un ejemplo que calcula la distancia de Minkowski para distintos valores de p:

import numpy as np
from scipy.spatial import distance

# Example points
point_a = [2, 3]
point_b = [5, 7]

# Different p values
p_values = [1, 2, 3, 10, np.inf]
print("Minkowski distances using SciPy:")

for p in p_values:
	if np.isinf(p):
	    # For p = infinity, use Chebyshev distance
	    dist = distance.chebyshev(point_a, point_b)
	    print(f"p = ∞, Distance = {dist:.2f}")
	else:
	        dist = distance.minkowski(point_a, point_b, p)
	        print(f"p = {p}, Distance = {dist:.2f}")

Al ejecutar este código, los lectores pueden observar cómo cambia la distancia con diferentes valores de p, reforzando los conceptos discutidos anteriormente en el artículo.

Minkowski distances using SciPy:
p = 1, Distance = 7.00
p = 2, Distance = 5.00
p = 3, Distance = 4.50
p = 10, Distance = 4.02
p = ∞, Distance = 4.00

Este código lo demuestra:

1. Cómo utilizar las funciones de distancia de SciPy para las distancias de Minkowski y Chebyshev.
2. Cálculo de distancias para diversos valores de p, incluido el infinito.
3. La relación entre la distancia de Minkowski y otras métricas (Manhattan, Euclídea, Chebyshev).

R ejemplo

Para R, utilizaremos la función dist() de la biblioteca stats:

# Define the Minkowski distance function using stats::dist

minkowski_distance <- function(x, y, p) {
  points <- rbind(x, y)
  if (is.infinite(p)) {
    # For p = Inf, use method = "maximum" for Chebyshev distance
    distance <- stats::dist(points, method = "maximum")
  } else {
    distance <- stats::dist(points, method = "minkowski", p = p)
  }
  return(as.numeric(distance))
}

# Example usage
point_a <- c(2, 3)
point_b <- c(5, 7)

# Different p values
p_values <- c(1, 2, 3, 10, Inf)
cat("Minkowski distances between points A and B using stats::dist:\n")

for (p in p_values) {
  distance <- minkowski_distance(point_a, point_b, p)
  if (is.infinite(p)) {
    cat(sprintf("p = ∞, Distance = %.2f\n", distance))
  } else {
    cat(sprintf("p = %g, Distance = %.2f\n", p, distance))
  }
}

Este código lo demuestra:

1. Cómo crear una función minkowski_distance utilizando la función dist() de stats.

2. Manejo de distintos valores de p, incluido el infinito para la distancia de Chebyshev.

3. Cálculo de la distancia de Minkowski para distintos valores de p.

4. Formatear la salida para mostrar las distancias redondeadas a 2 decimales.

La salida de este código será

Minkowski distances between points A and B using stats::dist:
p = 1, Distance = 7.00
p = 2, Distance = 5.00
p = 3, Distance = 4.50
p = 10, Distance = 4.02
p = ∞, Distance = 4.00

Esta implementación en R proporciona una contrapartida al ejemplo de Python, permitiendo a los lectores ver cómo se puede calcular la distancia de Minkowski en distintos entornos de programación.

Conclusión

La distancia de Minkowski proporciona un enfoque flexible y adaptable para medir distancias en espacios multidimensionales. Su capacidad para generalizar otras métricas de distancia comunes mediante el parámetro p la convierte en una herramienta valiosa en diversos campos de la ciencia de datos y el aprendizaje automático. Ajustando p, los profesionales pueden adaptar sus cálculos de distancia a las características específicas de sus datos y a los requisitos de sus proyectos, mejorando potencialmente los resultados en tareas que van desde la agrupación hasta la detección de anomalías.

Cuando apliques la distancia de Minkowski en tu propio trabajo, te animamos a que experimentes con distintos valores de p y observes su impacto en tus resultados. Para quienes deseen profundizar en sus conocimientos y habilidades, recomendamos explorar el curso Diseño de flujos de trabajo de aprendizaje automático en Python y considerar nuestro programa profesional de Certificación de Científico de Datos. Estos recursos pueden ayudarte a ampliar tus conocimientos sobre las métricas de distancia y a aplicarlas eficazmente en diversos escenarios.