Minkowski Distance: Um guia abrangente

As métricas de distância formam a espinha dorsal de vários algoritmos em ciência de dados e aprendizado de máquina, permitindo a medição de similaridade ou dissimilaridade entre pontos de dados. Neste guia, exploraremos os fundamentos da distância de Minkowski, suas propriedades matemáticas e suas implementações. Examinaremos como ela se relaciona com outras medidas de distância comuns e demonstraremos seu uso por meio de exemplos de codificação em Python e R. 

Se você estiver desenvolvendo algoritmos de agrupamento, trabalhando na detecção de anomalias ou ajustando modelos de classificação, a compreensão da distância de Minkowski pode aprimorar sua abordagem à análise de dados e ao desenvolvimento de modelos. Vamos dar uma olhada.

O que é a distância de Minkowski?

A distância de Minkowski é uma métrica versátil usada em espaços vetoriais normalizados, cujo nome é uma homenagem ao matemático alemão Hermann Minkowski. É uma generalização de várias medidas de distância conhecidas, tornando-a um conceito fundamental em vários campos, como matemática, ciência da computação e análise de dados.

Em sua essência, a distância de Minkowski oferece uma maneira de medir a distância entre dois pontos em um espaço multidimensional. O que o torna particularmente útil é sua capacidade de abranger outras métricas de distância como casos especiais, principalmente por meio de um parâmetro p. Esse parâmetro permite que a distância de Minkowski se adapte a diferentes espaços de problemas e características de dados. A fórmula geral da distância de Minkowski é:

Onde:

• x e y são dois pontos em um espaço n-dimensional

• p é um parâmetro que determina o tipo de distância (p ≥ 1)

• |xi - yi| representa a diferença absoluta entre as coordenadas de x e y em cada dimensão

A distância de Minkowski é útil por dois motivos principais. Por um lado, ele oferece a você a flexibilidade de alternar entre a distância de Manhattan ou a distância euclidiana, conforme necessário. Em segundo lugar, ele reconhece que nem todos os conjuntos de dados (pense em espaços de alta dimensão) são adequados para a distância puramente de Manhattan ou puramente euclidiana.

Na prática, o parâmetro p é normalmente escolhido pela incorporação de um fluxo de trabalho de validação de treinamento/teste. Ao testar diferentes valores de p durante a validação cruzada, você pode determinar qual valor oferece o melhor desempenho do modelo para o seu conjunto de dados específico.

Como funciona a distância de Minkowski

Vamos dar uma olhada em como a distância de Minkowski se relaciona com outras fórmulas de distância e, em seguida, veremos um exemplo. 

Generalização de outras métricas de distância

A primeira coisa a considerar é como a fórmula da distância de Minkowski contém as fórmulas das distâncias de Manhattan, Euclidiana e Chebyshev. 

Distância de Manhattan (p = 1): 

Quando p é definido como 1, a distância de Minkowski se torna a distância de Manhattan. 

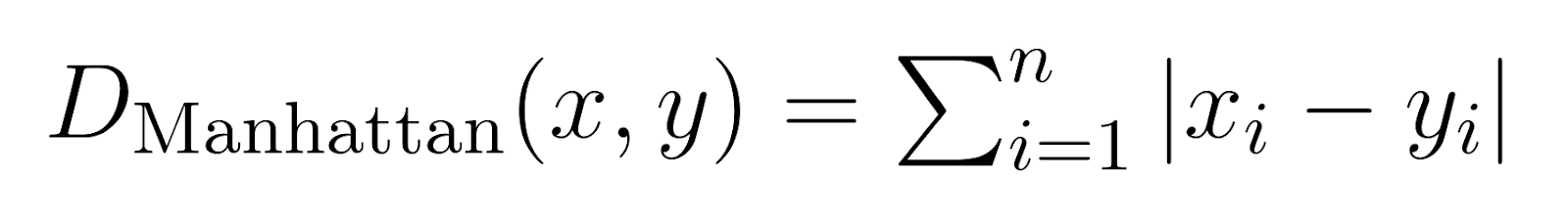
Também conhecida como distância entre quarteirões ou norma L1, a distância de Manhattan mede a soma das diferenças absolutas. 

Distância euclidiana (p = 2): 

Quando p é definido como 2, a distância de Minkowski se torna uma distância euclidiana.

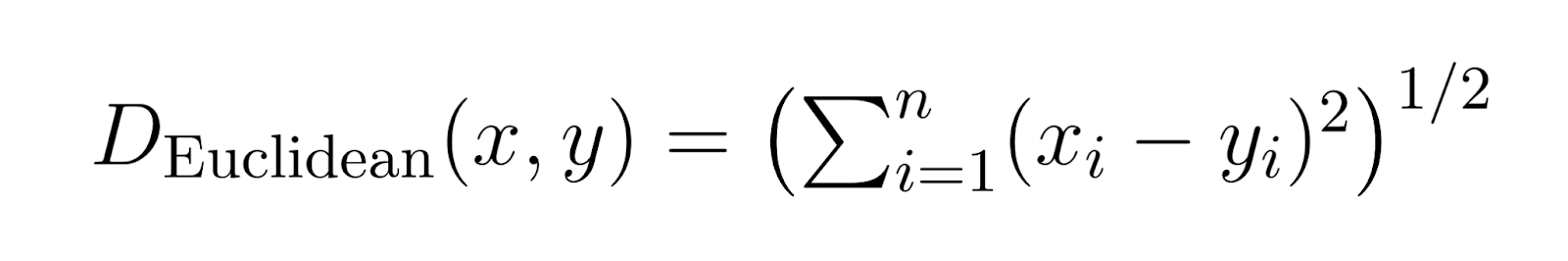
A distância euclidiana é a métrica de distância mais comum, representando a distância em linha reta entre dois pontos. 

Distância de Chebyshev (p → ∞): 

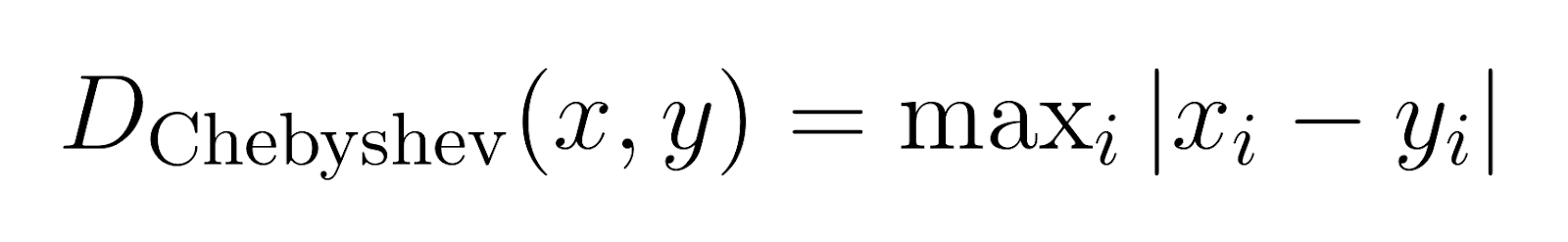
A distância de Chebyshev, também conhecida como distância do tabuleiro de xadrez, mede a diferença máxima ao longo de qualquer dimensão. 

Trabalhando com um exemplo

Para que você realmente entenda a funcionalidade e o poder da distância de Minkowski, vamos ver um exemplo. Essa exploração nos ajudará a entender como o parâmetro p afeta o cálculo e a interpretação das distâncias em espaços multidimensionais.

Vamos considerar dois pontos em um espaço 2D:

• Ponto A: (2, 3)
• Ponto B: (5, 7)

Calcularemos a distância de Minkowski entre esses pontos para diferentes valores de p.

O parâmetro p na fórmula da distância de Minkowski controla a sensibilidade da métrica às diferenças em componentes individuais:

• Quando p=1: Todas as diferenças contribuem linearmente.
• When p=2: Diferenças maiores têm um impacto mais significativo devido ao quadrado.
• Quando p>2: A ênfase é ainda maior nas diferenças maiores.
• Quando p→∞: Somente a diferença máxima entre todas as dimensões é importante.

À medida que p aumenta, a distância de Minkowski geralmente diminui, aproximando-se da distância de Chebyshev. Isso ocorre porque os valores mais altos de p dão mais peso à maior diferença e menos às diferenças menores.

Para visualizar como diferentes valores de p afetam o cálculo da distância entre os pontos A(2, 3) e B(5, 7), vamos examinar o gráfico a seguir:

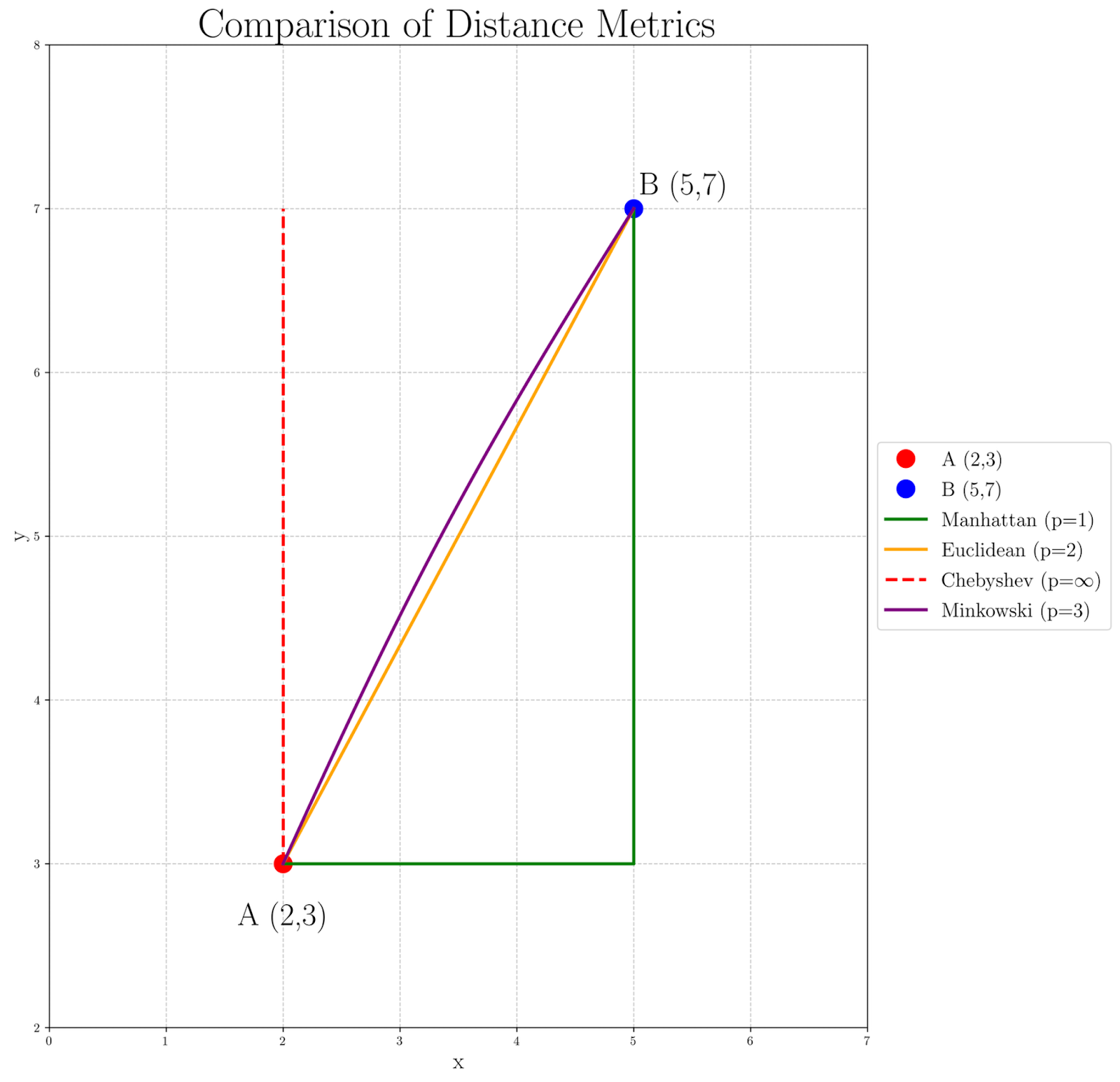
Observando o gráfico, podemos ver como a medida de distância muda à medida que p aumenta:

• A distância de Manhattan (p=1), representada pelo caminho verde, produz o caminho mais longo, pois segue estritamente a grade.
• A distância euclidiana (p=2), mostrada pela linha reta laranja, fornece um caminho direto e em linha reta.
• A distância de Chebyshev (p=∞), representada pelas linhas tracejadas vermelhas, concentra-se apenas na maior diferença de coordenadas, criando um caminho que se move ao máximo em uma dimensão antes de abordar a outra.
• A distância de Minkowski com p=3 em roxo mostra uma leve curva, indicando a transição entre as distâncias euclidiana e de Chebyshev.

Essa visualização nos ajuda a entender por que diferentes valores de p podem ser escolhidos para várias aplicações. Por exemplo, a distância de Manhattan pode ser mais apropriada para problemas de navegação em cidades, enquanto a distância euclidiana é usada com frequência em cálculos de espaço físico. Valores mais altos de p, como no caso de Minkowski p=3, podem ser úteis em cenários em que diferenças maiores devem ser enfatizadas, e a distância de Chebyshev pode ser preferida quando a diferença máxima em qualquer dimensão for o fator mais crítico.

Aplicações da distância de Minkowski

A distância de Minkowski, com seu parâmetro ajustável p, é uma ferramenta flexível usada em vários campos. Ao alterar o endereço p, podemos adaptar a forma como medimos a distância entre os pontos, tornando-a adequada para diferentes tarefas. Abaixo estão quatro aplicações em que a distância de Minkowski desempenha um papel importante.

Aprendizado de máquina e ciência de dados

No aprendizado de máquina e na ciência de dados, a distância de Minkowski é fundamental para algoritmos que dependem da medição da similaridade ou dissimilaridade entre pontos de dados. Um exemplo importante é o algoritmo k-Nearest Neighbors (k-NN), que classifica os pontos de dados com base nas categorias de seus vizinhos mais próximos. Ao usar a distância de Minkowski, podemos ajustar o parâmetro p para alterar a forma como calculamos a "proximidade" entre os pontos.

Reconhecimento de padrões

O reconhecimento de padrões envolve a identificação de padrões e regularidades nos dados, como o reconhecimento de escrita à mão ou a detecção de características faciais. Nesse contexto, a distância de Minkowski mede a diferença entre os vetores de recursos que representam padrões. Por exemplo, no reconhecimento de imagens, cada imagem pode ser representada por um vetor de valores de pixel. O cálculo da distância de Minkowski entre esses vetores nos permite quantificar a semelhança ou a diferença entre as imagens.

Ajustando p, podemos controlar a sensibilidade da medida de distância às diferenças em recursos específicos. Um p mais baixo pode considerar diferenças gerais em todos os pixels, enquanto um p mais alto pode enfatizar diferenças significativas em determinadas regiões da imagem.

Detecção de anomalias

A detecção de anomalias visa identificar pontos de dados que se desviam significativamente da maioria, o que é fundamental em áreas como detecção de fraudes, segurança de rede e detecção de falhas em sistemas. A distância de Minkowski é usada para medir a distância entre um ponto de dados e outros no conjunto de dados. Pontos com grandes distâncias são possíveis anomalias. Ao escolher um p adequado, os analistas podem aumentar a sensibilidade dos sistemas de detecção de anomalias aos tipos de desvios mais relevantes para o contexto específico.

Geometria computacional e análise espacial

Na geometria computacional e na análise espacial, a distância de Minkowski é usada para calcular distâncias entre pontos no espaço, o que é a base de muitos algoritmos geométricos. Por exemplo, a detecção de colisão nesses domínios se baseia na distância de Minkowski para determinar quando os objetos estão próximos o suficiente para interagir. Ao ajustar p, os desenvolvedores podem criar diversos limites de colisão, variando de angular ( p mais baixo) a arredondado ( p mais alto).

Além da detecção de colisões, a distância de Minkowski pode ser útil no agrupamento espacial e na análise de formas. A variação do valor de p permite que os pesquisadores enfatizem diferentes aspectos das relações espaciais, desde distâncias entre quarteirões até semelhanças de formas gerais.

Propriedades matemáticas da distância de Minkowski

A distância de Minkowski não é apenas uma ferramenta versátil em aplicações práticas, mas também um conceito importante na teoria matemática, especialmente no estudo de espaços métricos e normas.

Propriedades do espaço métrico

A distância de Minkowski satisfaz as quatro propriedades essenciais necessárias para que uma função seja considerada uma métrica em um espaço métrico:

• Não negatividade: A distância de Minkowski entre dois pontos quaisquer é sempre não negativa, d(x,y)≥0. Isso é evidente, pois é a raiz p-ésima de uma soma de termos não negativos (valores absolutos elevados à potência p).
• Identidade dos indiscerníveis: A distância de Minkowski entre dois pontos é zero se e somente se os dois pontos forem idênticos. Matematicamente, d(x,y) = 0 se e somente se x=y. Isso ocorre porque a diferença absoluta entre componentes idênticos é zero.
• Symmetry: A distância de Minkowski é simétrica, o que significa que d(x,y)=d(y,x). Essa propriedade se mantém porque a ordem de subtração nos termos de valor absoluto não afeta o resultado.
• Desigualdade de triângulos: A distância de Minkowski satisfaz a desigualdade triangular, que afirma que, para quaisquer três pontos x, y e z, a distância de x a z é, no máximo, a soma da distância de x a y e de y a z; formalmente, d(x,z)≤d(x,y)+d(y,z). Essa propriedade é menos intuitiva de ser comprovada diretamente pela fórmula e, em geral, requer matemática mais avançada, mas basicamente garante que seguir um caminho direto entre dois pontos é a rota mais curta.

Generalização de normas

A distância de Minkowski funciona como uma estrutura geral que unifica várias maneiras de medir distâncias em espaços matemáticos por meio do conceito de normas. Em termos simples, umanorma é uma função que atribui um comprimento ou tamanho não negativo a um vetor em um espaço vetorial, medindo essencialmente o "comprimento" do vetor. Ao ajustar o parâmetro p na fórmula da distância de Minkowski, podemos fazer uma transição suave entre diferentes normas, cada uma fornecendo um método exclusivo para calcular o comprimento do vetor.

Por exemplo, quando p=1, a distância de Minkowski se torna a norma de Manhattan, medindo a distância como a soma das diferenças absolutas ao longo de cada dimensão - imagine navegar em uma grade de ruas da cidade. Com p=2, ele se transforma nanorma euclidiana , calculando a distância em linha reta ("as-the-crow-flies") entre os pontos. À medida que p se aproxima do infinito, ela converge para anorma de Chebyshev , em que a distância é determinada pela maior diferença individual entre as dimensões. Essa flexibilidade permite que a distância de Minkowski se adapte a vários contextos matemáticos e práticos, tornando-a uma ferramenta versátil para medir distâncias em diferentes cenários.

Cálculo da distância de Minkowski em Python e R

Vamos explorar as implementações dos cálculos da distância de Minkowski usando Python e R. Examinaremos pacotes e bibliotecas prontamente disponíveis que podem fazer isso. 

Exemplo de Python

Para calcular a distância de Minkowski em Python, podemos usar a biblioteca SciPy, que fornece implementações eficientes de várias métricas de distância. Aqui está um exemplo que calcula a distância de Minkowski para diferentes valores de p:

import numpy as np
from scipy.spatial import distance

# Example points
point_a = [2, 3]
point_b = [5, 7]

# Different p values
p_values = [1, 2, 3, 10, np.inf]
print("Minkowski distances using SciPy:")

for p in p_values:
	if np.isinf(p):
	    # For p = infinity, use Chebyshev distance
	    dist = distance.chebyshev(point_a, point_b)
	    print(f"p = ∞, Distance = {dist:.2f}")
	else:
	        dist = distance.minkowski(point_a, point_b, p)
	        print(f"p = {p}, Distance = {dist:.2f}")

Ao executar esse código, os leitores podem observar como a distância muda com diferentes valores de p, reforçando os conceitos discutidos anteriormente no artigo.

Minkowski distances using SciPy:
p = 1, Distance = 7.00
p = 2, Distance = 5.00
p = 3, Distance = 4.50
p = 10, Distance = 4.02
p = ∞, Distance = 4.00

Este código demonstra:

1. Como usar as funções de distância do SciPy para as distâncias de Minkowski e Chebyshev.
2. Cálculo de distâncias para vários valores de p, incluindo o infinito.
3. A relação entre a distância de Minkowski e outras métricas (Manhattan, Euclidean, Chebyshev).

Exemplo de R

No R, utilizaremos a função dist() da biblioteca stats:

# Define the Minkowski distance function using stats::dist

minkowski_distance <- function(x, y, p) {
  points <- rbind(x, y)
  if (is.infinite(p)) {
    # For p = Inf, use method = "maximum" for Chebyshev distance
    distance <- stats::dist(points, method = "maximum")
  } else {
    distance <- stats::dist(points, method = "minkowski", p = p)
  }
  return(as.numeric(distance))
}

# Example usage
point_a <- c(2, 3)
point_b <- c(5, 7)

# Different p values
p_values <- c(1, 2, 3, 10, Inf)
cat("Minkowski distances between points A and B using stats::dist:\n")

for (p in p_values) {
  distance <- minkowski_distance(point_a, point_b, p)
  if (is.infinite(p)) {
    cat(sprintf("p = ∞, Distance = %.2f\n", distance))
  } else {
    cat(sprintf("p = %g, Distance = %.2f\n", p, distance))
  }
}

Este código demonstra:

1. Como você pode criar uma função minkowski_distance usando a função dist() de stats.

2. Manuseio de diferentes valores de p, incluindo infinito para a distância de Chebyshev.

3. Cálculo da distância de Minkowski para vários valores de p.

4. Formatar a saída para exibir distâncias arredondadas para 2 casas decimais.

O resultado desse código será:

Minkowski distances between points A and B using stats::dist:
p = 1, Distance = 7.00
p = 2, Distance = 5.00
p = 3, Distance = 4.50
p = 10, Distance = 4.02
p = ∞, Distance = 4.00

Essa implementação em R fornece uma contrapartida para o exemplo em Python, permitindo que os leitores vejam como a distância de Minkowski pode ser calculada em diferentes ambientes de programação.

Conclusão

A distância de Minkowski oferece uma abordagem flexível e adaptável para medir distâncias em espaços multidimensionais. Sua capacidade de generalizar outras métricas de distância comuns por meio do parâmetro p torna-o uma ferramenta valiosa em vários campos da ciência de dados e do aprendizado de máquina. Ajustando p, os profissionais podem adaptar seus cálculos de distância às características específicas de seus dados e aos requisitos de seus projetos, melhorando potencialmente os resultados em tarefas que vão desde o agrupamento até a detecção de anomalias.

Ao aplicar a distância de Minkowski em seu próprio trabalho, recomendamos que você faça experiências com diferentes valores de p e observe o impacto deles nos resultados. Para aqueles que desejam aprofundar seus conhecimentos e habilidades, recomendamos que você explore o curso Designing Machine Learning Workflows in Python e considere nosso programa de carreira de Certificação de Cientista de Dados. Esses recursos podem ajudar você a desenvolver seu conhecimento sobre métricas de distância e aplicá-las de forma eficaz em vários cenários.