Minkowski-Entfernung: Ein umfassender Leitfaden

Distanzmetriken bilden das Rückgrat zahlreicher Algorithmen in der Datenwissenschaft und im maschinellen Lernen und ermöglichen die Messung der Ähnlichkeit oder Unähnlichkeit zwischen Datenpunkten. In diesem Leitfaden werden wir die Grundlagen der Minkowski-Distanz, ihre mathematischen Eigenschaften und ihre Implementierungen erkunden. Wir werden untersuchen, wie es sich zu anderen gängigen Abstandsmaßen verhält und seine Anwendung anhand von Programmierbeispielen in Python und R demonstrieren. 

Ganz gleich, ob du Clustering-Algorithmen entwickelst, an der Erkennung von Anomalien arbeitest oder Klassifizierungsmodelle fein abstimmst, das Verständnis der Minkowski-Distanz kann deine Herangehensweise an die Datenanalyse und Modellentwicklung verbessern. Schauen wir uns das mal an.

Was ist die Minkowski-Distanz?

Der Minkowski-Abstand ist eine vielseitige Metrik, die in normierten Vektorräumen verwendet wird und nach dem deutschen Mathematiker Hermann Minkowski benannt ist. Sie ist eine Verallgemeinerung mehrerer bekannter Abstandsmaße und damit ein grundlegendes Konzept in verschiedenen Bereichen wie Mathematik, Informatik und Datenanalyse.

Im Kern bietet die Minkowski-Distanz eine Möglichkeit, den Abstand zwischen zwei Punkten in einem mehrdimensionalen Raum zu messen. Was ihn besonders nützlich macht, ist seine Fähigkeit, andere Abstandsmetriken als Sonderfälle einzubeziehen, vor allem durch einen Parameter p. Mit diesem Parameter lässt sich die Minkowski-Distanz an unterschiedliche Problemräume und Datenmerkmale anpassen. Die allgemeine Formel für die Minkowski-Distanz lautet:

Wo:

• x und y sind zwei Punkte in einem n-dimensionalen Raum

• p ist ein Parameter, der die Art der Entfernung bestimmt (p ≥ 1)

• |xi - yi| steht für die absolute Differenz zwischen den Koordinaten von x und y in jeder Dimension

Die Minkowski-Distanz ist vor allem aus zwei Gründen nützlich. Zum einen kannst du flexibel zwischen der Manhattan- und der Euklidischen Distanz umschalten, je nach Bedarf. Zweitens erkennt sie an, dass nicht alle Datensätze (z. B. hochdimensionale Räume) für die reine Manhattan- oder die reine euklidische Distanz geeignet sind.

In der Praxis wird der Parameter p in der Regel mit Hilfe eines Train/Test-Validierungsworkflows ausgewählt. Indem du während der Kreuzvalidierung verschiedene Werte von p testest, kannst du herausfinden, welcher Wert die beste Modellleistung für deinen spezifischen Datensatz liefert.

Wie der Minkowski-Abstand funktioniert

Schauen wir uns an, wie sich die Minkowski-Distanz zu anderen Distanzformeln verhält, und gehen dann ein Beispiel durch. 

Verallgemeinerung anderer Distanzmetriken

Zunächst einmal ist zu beachten, dass die Minkowski-Entfernungsformel die Formeln für Manhattan-, Euklidische- und Tschebyscheff-Entfernungen enthält. 

Manhattan Distance (p = 1): 

Wenn p auf 1 gesetzt wird, wird die Minkowski-Distanz zur Manhattan-Distanz. 

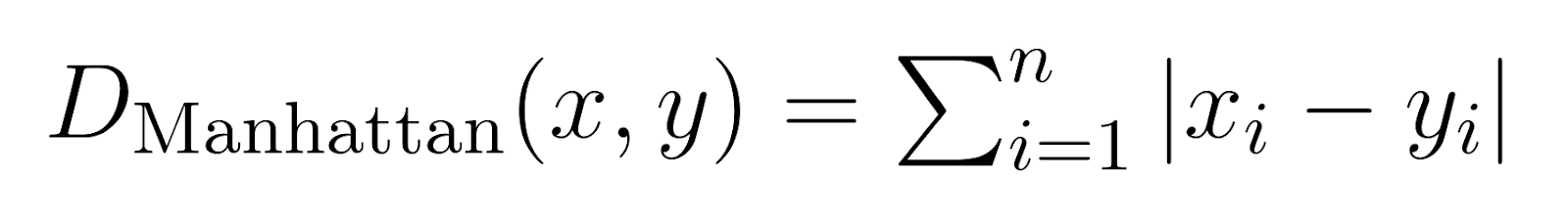
Die Manhattan-Distanz, auch bekannt als City-Block-Distanz oder L1-Norm, misst die Summe der absoluten Unterschiede. 

Euklidischer Abstand (p = 2): 

Wenn p auf 2 gesetzt wird, wird der Minkowski-Abstand zum euklidischen Abstand.

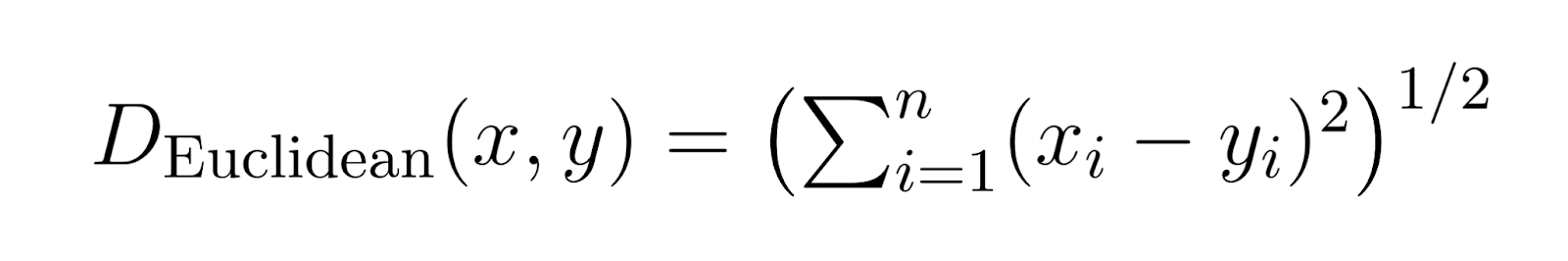
Die euklidische Distanz ist die gebräuchlichste Distanzmetrik, die den geradlinigen Abstand zwischen zwei Punkten darstellt. 

Tschebyscheff-Abstand (p → ∞): 

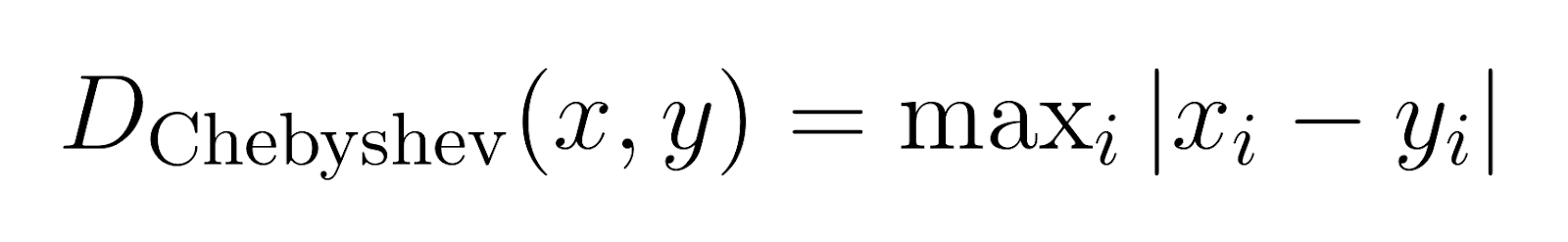
Der Tschebyscheff-Abstand, auch bekannt als Schachbrett-Abstand, misst die maximale Differenz entlang einer beliebigen Dimension. 

Ein Beispiel durcharbeiten

Um die Funktionsweise und Macht der Minkowski-Distanz wirklich zu verstehen, lass uns ein Beispiel durchspielen. Diese Erkundung wird uns helfen zu verstehen, wie der Parameter p die Berechnung und Interpretation von Entfernungen in mehrdimensionalen Räumen beeinflusst.

Betrachten wir zwei Punkte in einem 2D-Raum:

• Punkt A: (2, 3)
• Punkt B: (5, 7)

Wir werden den Minkowski-Abstand zwischen diesen Punkten für verschiedene p Werte berechnen.

Der Parameter p in der Minkowski-Distanzformel steuert die Empfindlichkeit der Metrik gegenüber Unterschieden in einzelnen Komponenten:

• Wenn p=1: Alle Unterschiede tragen linear zueinander bei.
• Wenn p=2: Größere Unterschiede wirken sich durch die Quadratur stärker aus.
• Wenn p>2: Größere Unterschiede werden noch stärker betont.
• Wenn p→∞: Es zählt nur der maximale Unterschied zwischen allen Dimensionen.

Wenn p zunimmt, wird der Minkowski-Abstand im Allgemeinen kleiner und nähert sich dem Tschebyscheff-Abstand an. Das liegt daran, dass höhere p Werte dem größten Unterschied mehr Gewicht geben und den kleineren Unterschieden weniger.

Um zu veranschaulichen, wie sich verschiedene Werte von p auf die Berechnung der Entfernung zwischen den Punkten A(2, 3) und B(5, 7) auswirken, schauen wir uns die folgende Grafik an:

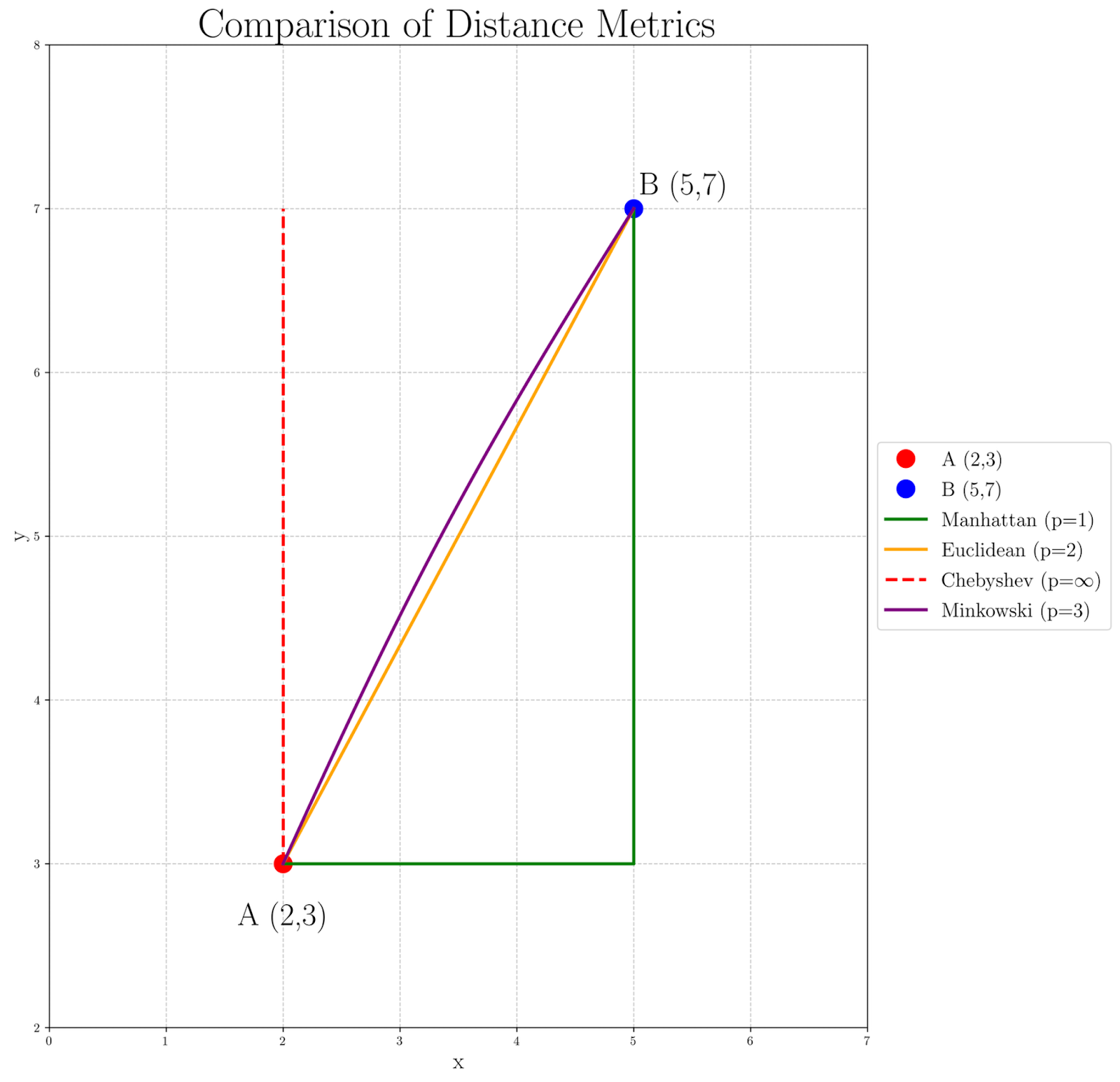
Anhand des Diagramms können wir sehen, wie sich das Abstandsmaß ändert, wenn p zunimmt:

• Die Manhattan-Distanz (p=1), dargestellt durch den grünen Pfad, ergibt den längsten Pfad, da er streng dem Raster folgt.
• Die euklidische Entfernung (p=2), dargestellt durch die orangefarbene Gerade, bietet einen direkten, geradlinigen Weg.
• Die Tschebyscheff-Distanz (p=∞), dargestellt durch die rot gestrichelten Linien, konzentriert sich ausschließlich auf die größte Koordinatendifferenz und erzeugt einen Pfad, der sich maximal in einer Dimension bewegt, bevor er die andere anspricht.
• Der Minkowski-Abstand mit p=3 in lila zeigt eine leichte Kurve, die den Übergang zwischen euklidischen und Tschebyscheff-Abständen andeutet.

Diese Visualisierung hilft uns zu verstehen, warum unterschiedliche p Werte für verschiedene Anwendungen gewählt werden. Die Manhattan-Distanz eignet sich zum Beispiel besser für die Navigation in Städten, während die euklidische Distanz oft für Berechnungen im physischen Raum verwendet wird. Höhere p Werte, wie im Fall von Minkowski p=3, können in Szenarien nützlich sein, in denen größere Unterschiede hervorgehoben werden sollen, und der Tschebyscheff-Abstand kann bevorzugt werden, wenn der maximale Unterschied in einer Dimension der kritischste Faktor ist.

Anwendungen der Minkowski-Distanz

Der Minkowski-Abstand mit seinem einstellbaren Parameter p ist ein flexibles Werkzeug, das in verschiedenen Bereichen eingesetzt wird. Indem wir p ändern, können wir die Messung des Abstands zwischen den Punkten anpassen, sodass sie für verschiedene Aufgaben geeignet ist. Im Folgenden findest du vier Anwendungen, bei denen die Minkowski-Distanz eine wichtige Rolle spielt.

Maschinelles Lernen und Datenwissenschaft

Beim maschinellen Lernen und in der Datenwissenschaft ist die Minkowski-Distanz von grundlegender Bedeutung für Algorithmen, die die Ähnlichkeit oder Unähnlichkeit zwischen Datenpunkten messen. Ein bekanntes Beispiel ist der k-Nächste-Nachbarn-Algorithmus (k-NN), der Datenpunkte auf der Grundlage der Kategorien ihrer nächsten Nachbarn klassifiziert. Wenn wir die Minkowski-Distanz verwenden, können wir den Parameter p anpassen, um zu ändern, wie wir die "Nähe" zwischen Punkten berechnen.

Mustererkennung

Bei der Mustererkennung geht es darum, Muster und Regelmäßigkeiten in Daten zu erkennen, z. B. bei der Handschrifterkennung oder der Erkennung von Gesichtsmerkmalen. In diesem Zusammenhang misst die Minkowski-Distanz den Unterschied zwischen Merkmalsvektoren, die Muster darstellen. Bei der Bilderkennung zum Beispiel kann jedes Bild durch einen Vektor von Pixelwerten dargestellt werden. Durch die Berechnung der Minkowski-Distanz zwischen diesen Vektoren können wir quantifizieren, wie ähnlich oder unterschiedlich die Bilder sind.

Durch die Anpassung von p können wir die Empfindlichkeit des Abstandsmaßes gegenüber Unterschieden in bestimmten Merkmalen steuern. Eine niedrigere p kann die Gesamtunterschiede zwischen allen Pixeln berücksichtigen, während eine höhere p die signifikanten Unterschiede in bestimmten Regionen des Bildes hervorheben kann.

Erkennung von Anomalien

Die Erkennung von Anomalien zielt darauf ab, Datenpunkte zu identifizieren, die signifikant von der Mehrheit abweichen, was in Bereichen wie Betrugserkennung, Netzwerksicherheit und Fehlererkennung in Systemen entscheidend ist. Die Minkowski-Distanz wird verwendet, um zu messen, wie weit ein Datenpunkt von anderen im Datensatz entfernt ist. Punkte mit großen Abständen sind potenzielle Anomalien. Durch die Wahl eines geeigneten p können Analysten die Empfindlichkeit von Systemen zur Erkennung von Anomalien für die Arten von Abweichungen verbessern, die für ihren spezifischen Kontext am wichtigsten sind.

Computergestützte Geometrie und räumliche Analyse

In der Computergeometrie und der Raumanalyse wird die Minkowski-Distanz verwendet, um Abstände zwischen Punkten im Raum zu berechnen, was die Grundlage für viele geometrische Algorithmen ist. Zum Beispiel beruht die Kollisionserkennung in diesen Bereichen auf der Minkowski-Distanz, um zu bestimmen, wann Objekte nahe genug sind, um miteinander zu interagieren. Durch die Anpassung von p können Entwickler verschiedene Kollisionsgrenzen erstellen, die von eckig (niedrigeres p) bis zu abgerundet (höheres p) reichen.

Neben der Kollisionserkennung kann die Minkowski-Distanz auch bei der räumlichen Clusterbildung und der Formanalyse nützlich sein. Durch die Variation des Werts von p können die Forscher verschiedene Aspekte der räumlichen Beziehungen betonen, von der Entfernung zwischen den Häuserblocks bis hin zu Ähnlichkeiten in der Gesamtform.

Mathematische Eigenschaften der Minkowski-Distanz

Der Minkowski-Abstand ist nicht nur ein vielseitiges Werkzeug in der Praxis, sondern auch ein wichtiges Konzept in der mathematischen Theorie, insbesondere bei der Untersuchung von metrischen Räumen und Normen.

Eigenschaften des metrischen Raums

Die Minkowski-Distanz erfüllt die vier wesentlichen Eigenschaften, die eine Funktion erfüllen muss, um als metrisch in einem metrischen Raum zu gelten:

• Nicht-Negativität: Der Minkowski-Abstand zwischen zwei beliebigen Punkten ist immer nicht-negativ, d(x,y)≥0. Das ist offensichtlich, denn es ist die p-te Wurzel aus einer Summe von nicht-negativen Termen (absolute Werte hoch p).
• Identität von Unsichtbarkeiten: Der Minkowski-Abstand zwischen zwei Punkten ist nur dann Null, wenn die beiden Punkte identisch sind. Mathematisch gesehen ist d(x,y) = 0, wenn und nur wenn x=y. Das folgt daraus, dass der absolute Unterschied zwischen identischen Komponenten gleich Null ist.
• Symmetrie: Der Minkowski-Abstand ist symmetrisch, d.h. d(x,y)=d(y,x). Diese Eigenschaft gilt, weil die Reihenfolge der Subtraktion in den Absolutwerttermen keinen Einfluss auf das Ergebnis hat.
• Dreiecks-Ungleichheit: Die Minkowski-Distanz erfüllt die Dreiecksungleichung, die besagt, dass für drei beliebige Punkte x, y und z der Abstand von x zu z höchstens die Summe der Abstände von x zu y und von y zu z ist; formal ausgedrückt: d(x,z)≤d(x,y)+d(y,z). Diese Eigenschaft ist weniger intuitiv direkt aus der Formel zu beweisen und erfordert in der Regel eine fortgeschrittenere Mathematik, stellt aber im Wesentlichen sicher, dass ein direkter Weg zwischen zwei Punkten die kürzeste Route ist.

Normverallgemeinerung

Die Minkowski-Distanz dient als allgemeiner Rahmen, der verschiedene Möglichkeiten zur Messung von Distanzen in mathematischen Räumen durch das Konzept der Normen vereinheitlicht. Vereinfacht ausgedrückt ist eine Norm eine Funktion, die einem Vektor in einem Vektorraum eine nicht-negative Länge oder Größe zuweist, also im Wesentlichen misst, wie "lang" der Vektor ist. Indem wir den Parameter p in der Minkowski-Distanzformel anpassen, können wir nahtlos zwischen verschiedenen Normen wechseln, die jeweils eine eigene Methode zur Berechnung der Vektorlänge bieten.

Wenn zum Beispiel p=1 ist, wird die Minkowski-Distanz zur Manhattan-Norm und misst die Distanz als Summe der absoluten Unterschiede entlang jeder Dimension - stell dir vor, du navigierst durch ein Straßennetz. Bei p=2 wird daraus die Euklidische Norm, die den geradlinigen ("wie die Krähe fliegt") Abstand zwischen Punkten berechnet. Wenn p sich der Unendlichkeit nähert, konvergiert sie gegen die Tschebyscheff-Norm, wobei der Abstand durch die größte einzelne Differenz zwischen den Dimensionen bestimmt wird. Dank dieser Flexibilität passt sich die Minkowski-Distanz an verschiedene mathematische und praktische Kontexte an, was sie zu einem vielseitigen Instrument zur Messung von Entfernungen in unterschiedlichen Szenarien macht.

Berechnung des Minkowski-Abstands in Python und R

Wir werden uns mit den Implementierungen von Minkowski-Distanzberechnungen in Python und R befassen und die verfügbaren Pakete und Bibliotheken untersuchen, die dies ermöglichen. 

Python Beispiel

Um die Minkowski-Distanz in Python zu berechnen, können wir die SciPy-Bibliothek verwenden, die effiziente Implementierungen verschiedener Distanzmetriken bietet. Hier ist ein Beispiel, das den Minkowski-Abstand für verschiedene p-Werte berechnet:

import numpy as np
from scipy.spatial import distance

# Example points
point_a = [2, 3]
point_b = [5, 7]

# Different p values
p_values = [1, 2, 3, 10, np.inf]
print("Minkowski distances using SciPy:")

for p in p_values:
	if np.isinf(p):
	    # For p = infinity, use Chebyshev distance
	    dist = distance.chebyshev(point_a, point_b)
	    print(f"p = ∞, Distance = {dist:.2f}")
	else:
	        dist = distance.minkowski(point_a, point_b, p)
	        print(f"p = {p}, Distance = {dist:.2f}")

Wenn du diesen Code ausführst, kannst du beobachten, wie sich der Abstand bei verschiedenen p-Werten ändert, und so die zuvor im Artikel besprochenen Konzepte vertiefen.

Minkowski distances using SciPy:
p = 1, Distance = 7.00
p = 2, Distance = 5.00
p = 3, Distance = 4.50
p = 10, Distance = 4.02
p = ∞, Distance = 4.00

Dieser Code demonstriert:

1. Wie du die SciPy-Funktionen für Minkowski- und Tschebyscheff-Distanzen verwendest.
2. Berechnung von Entfernungen für verschiedene p-Werte, einschließlich unendlich.
3. Die Beziehung zwischen der Minkowski-Distanz und anderen Metriken (Manhattan, Euklidisch, Tschebyscheff).

R Beispiel

Für R werden wir die Funktion dist() aus der Bibliothek stats verwenden:

# Define the Minkowski distance function using stats::dist

minkowski_distance <- function(x, y, p) {
  points <- rbind(x, y)
  if (is.infinite(p)) {
    # For p = Inf, use method = "maximum" for Chebyshev distance
    distance <- stats::dist(points, method = "maximum")
  } else {
    distance <- stats::dist(points, method = "minkowski", p = p)
  }
  return(as.numeric(distance))
}

# Example usage
point_a <- c(2, 3)
point_b <- c(5, 7)

# Different p values
p_values <- c(1, 2, 3, 10, Inf)
cat("Minkowski distances between points A and B using stats::dist:\n")

for (p in p_values) {
  distance <- minkowski_distance(point_a, point_b, p)
  if (is.infinite(p)) {
    cat(sprintf("p = ∞, Distance = %.2f\n", distance))
  } else {
    cat(sprintf("p = %g, Distance = %.2f\n", p, distance))
  }
}

Dieser Code demonstriert:

1. So erstellst du eine Funktion minkowski_distance, indem du die Funktion dist() von stats verwendest.

2. Umgang mit verschiedenen p-Werten, einschließlich unendlich für Tschebyscheff-Abstand.

3. Berechnung der Minkowski-Distanz für verschiedene p-Werte.

4. Formatierung der Ausgabe, um Entfernungen auf 2 Dezimalstellen gerundet anzuzeigen.

Die Ausgabe dieses Codes wird sein:

Minkowski distances between points A and B using stats::dist:
p = 1, Distance = 7.00
p = 2, Distance = 5.00
p = 3, Distance = 4.50
p = 10, Distance = 4.02
p = ∞, Distance = 4.00

Diese R-Implementierung ist das Gegenstück zum Python-Beispiel, damit die Leser/innen sehen können, wie die Minkowski-Distanz in verschiedenen Programmierumgebungen berechnet werden kann.

Fazit

Die Minkowski-Distanz bietet einen flexiblen und anpassungsfähigen Ansatz zur Messung von Distanzen in mehrdimensionalen Räumen. Seine Fähigkeit, andere gängige Distanzmetriken durch den Parameter p zu verallgemeinern, macht es zu einem wertvollen Werkzeug in verschiedenen Bereichen der Datenwissenschaft und des maschinellen Lernens. Durch die Anpassung von p können Praktiker ihre Abstandsberechnungen auf die spezifischen Merkmale ihrer Daten und die Anforderungen ihrer Projekte abstimmen und so potenziell bessere Ergebnisse bei Aufgaben vom Clustering bis zur Anomalieerkennung erzielen.

Wenn du die Minkowski-Distanz in deiner eigenen Arbeit anwendest, ermutigen wir dich, mit verschiedenen p-Werten zu experimentieren und ihre Auswirkungen auf deine Ergebnisse zu beobachten. Wenn du dein Wissen und deine Fähigkeiten vertiefen möchtest, empfehlen wir dir, den Kurs Designing Machine Learning Workflows in Python zu besuchen und unser Zertifizierungsprogramm für Data Scientists in Betracht zu ziehen. Diese Ressourcen können dir dabei helfen, dein Wissen über Distanzmetriken zu erweitern und sie in verschiedenen Szenarien effektiv anzuwenden.