¿Qué es la Distancia Manhattan?

."Distancia a Manhattan". Imagen de Dall-E.

Las métricas de distancia son herramientas esenciales para medir la distancia entre objetos o puntos del espacio. Estas métricas desempeñan un gran papel en muchos campos, como el aprendizaje automático, la robótica y los sistemas de información geográfica. Al cuantificar las distancias, podemos realizar tareas como el reconocimiento de patrones, la agrupación de datos y el análisis espacial, que son importantes tanto para las empresas con ánimo de lucro como para los investigadores. 

La distancia Manhattan, también conocida como distancia L1 o distancia taxi, destaca por ser una medida especialmente útil para calcular distancias en recorridos en forma de cuadrícula o entre puntos en espacios multidimensionales. Aquí veremos tanto el fundamento matemático como la forma de implementar la distancia Manhattan tanto en Python como en R. 

Ten en cuenta que la distancia Manhattan es sólo una parte del tema más amplio de las métricas de distancia, que aparecen una y otra vez en todo tipo de campos. Para convertirte en un experto en aprendizaje a distancia, considera nuestro curso de Diseño de flujos de trabajo de aprendizaje automático en Python o nuestro curso de Análisis de conglomerados en R, dependiendo del lenguaje que prefieras. 

Definir la distancia a Manhattan

La distancia Manhattan es una métrica utilizada para determinar la distancia entre dos puntos de una trayectoria en forma de cuadrícula. A diferencia de la distancia euclidiana, que mide la línea más corta posible entre dos puntos, la distancia de Manhattan mide la suma de las diferencias absolutas entre las coordenadas de los puntos. Este método se denomina "distancia Manhattan" porque, como un taxi que circula por las calles cuadriculadas de Manhattan, debe recorrer las líneas de la cuadrícula. 

Matemáticamente, la distancia Manhattan entre dos puntos de un espacio n-dimensional es la suma de las diferencias absolutas de sus coordenadas cartesianas. 

La fórmula de la distancia Manhattan incorpora la función del valor absoluto, que simplemente convierte cualquier diferencia negativa en un valor positivo. Esto es crucial para calcular la distancia, ya que garantiza que todas las mediciones de distancia sean no negativas, reflejando la verdadera distancia escalar independientemente de la dirección de desplazamiento.

Cálculo y visualización de la distancia Manhattan

Como hemos dicho, la distancia Manhattan se calcula sumando las diferencias absolutas entre las coordenadas correspondientes de dos puntos. Exploremos ahora esto con ejemplos en el espacio 2D y 3D.

Ejemplo 2D

Considera dos puntos: A(1, 1) y B(4, 5):

1. Calcula |x₁ - x₂| = |1 - 4| = 3
2. Calcula |y₁ - y₂| = |1 - 5| = 4
3. Suma los resultados: 3 + 4 = 7

Por tanto, la distancia Manhattan entre A y B es de 7 unidades. 

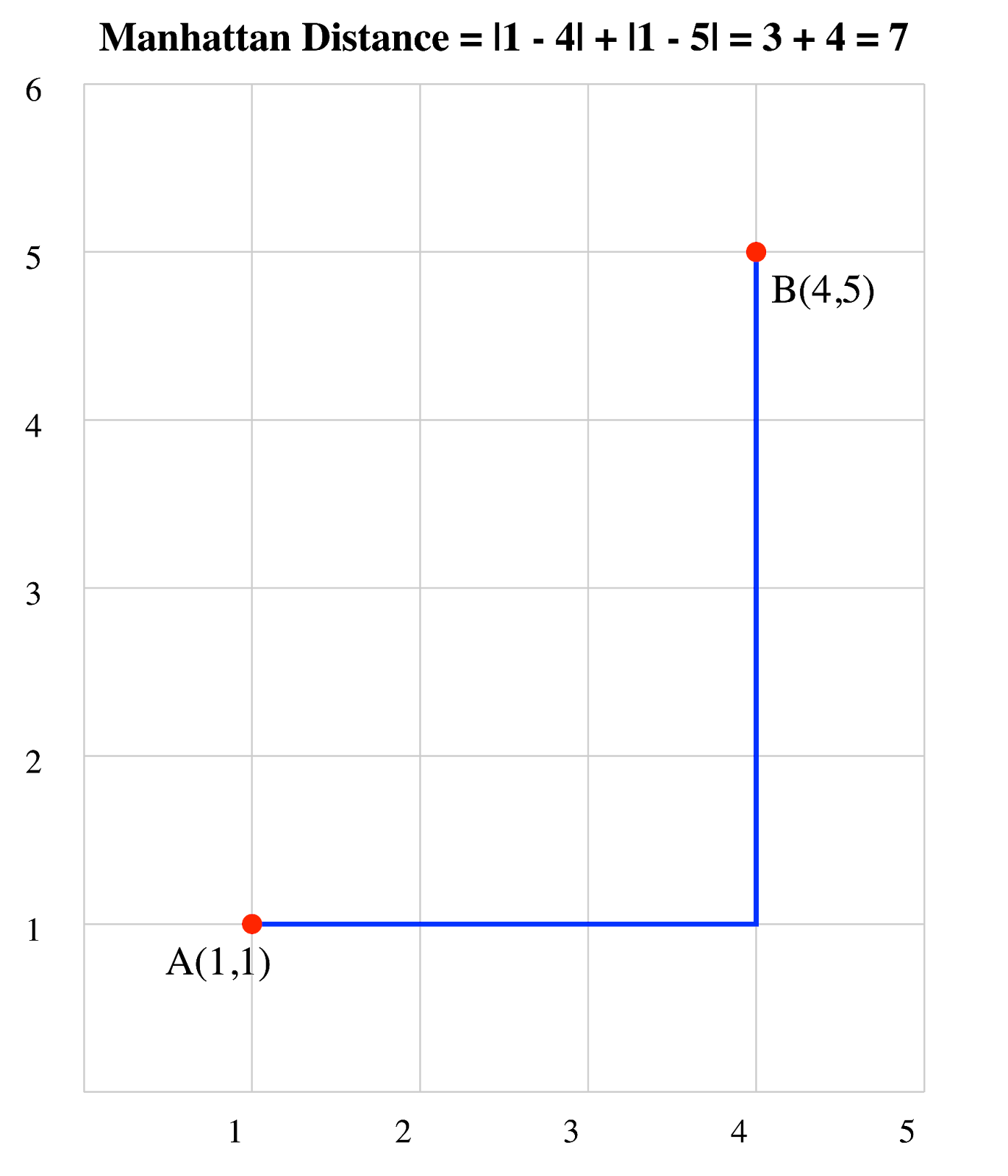Distancia Manhattan de dos Distancia Manhattan de dos vectores. Imagen del autor.

En esta cuadrícula 2D, puedes ver que la distancia Manhattan sigue la trayectoria que seguiría un taxi, moviéndose sólo horizontal y verticalmente para ir del punto A al punto B.

Ejemplo 3D

Consideremos ahora dos puntos en el espacio tridimensional: A(1, 2, 3) y B(4, 5, 6):

1. Calcula |x₁ - x₂| = |1 - 4| = 3
2. Calcula |y₁ - y₂| = |2 - 5| = 3
3. Calcula |z₁ - z₂| = |3 - 6| = 3
4. Suma los resultados: 3 + 3 + 3 = 9

La distancia Manhattan entre estos puntos 3D es de 9 unidades.

Comparación con la distancia euclidiana

Mientras que la distancia Manhattan mide el recorrido a lo largo de las líneas de la cuadrícula, la distancia euclidiana mide la distancia en línea recta entre dos puntos o, "a vuelo de pájaro", como se suele decir. 

Para nuestro ejemplo 2D:

• Distancia a Manhattan: 7 unidades
• Distancia euclidiana: √((1-4^)² + (1-5^)²) = 5 unidades

He aquí una comparación visual entre las distancias Manhattan y Euclidiana: 

Distancia de Manhattan vs. Distancia euclidiana. Imagen del autor.

En el espacio euclidiano, la distancia euclidiana es siempre menor o igual que la distancia Manhattan. 

Elegir entre la distancia Manhattan y la distancia euclidiana

La distancia de Manhattan es especialmente útil en situaciones en las que

1. El movimiento se limita a recorridos en forma de cuadrícula (por ejemplo, manzanas de una ciudad, trazados de placas de circuitos).
2. El movimiento diagonal no está permitido o es más costoso.
3. Trabajas con datos de alta dimensión en el aprendizaje automático, donde puede ser computacionalmente más eficiente que la distancia euclidiana.
4. Estás analizando diferencias en datos discretos u ordinales.

En cambio, la distancia euclidiana es más adecuada cuando:

1. Estás midiendo distancias físicas en espacios abiertos.
2. Estás trabajando con datos continuos en los que los movimientos diagonales son igualmente válidos.

Aplicaciones de la distancia Manhattan

La distancia Manhattan encuentra aplicaciones en diversos campos de la informática, el análisis de datos y la tecnología geoespacial. He aquí algunas áreas clave en las que la distancia Manhattan resulta especialmente útil.

Algoritmos de búsqueda de rutas (por ejemplo, el algoritmo A*) 

En entornos basados en cuadrículas, la distancia Manhattan proporciona una heurística rápida y eficaz para estimar la distancia entre dos puntos. Es especialmente útil en el algoritmo A*, donde puede ayudar a guiar la búsqueda hacia la meta de forma más eficiente en escenarios en los que el movimiento está restringido a las direcciones horizontal y vertical. Piensa en el trazado de las calles de una ciudad, en los algoritmos de resolución de laberintos y en ciertos tipos de búsqueda de trayectorias de la IA de los videojuegos. 

Técnicas de agrupación (por ejemplo, agrupación de K-Means) 

La distancia Manhattan puede utilizarse como métrica de distancia en los algoritmos de agrupación, sobre todo cuando se trata de datos de alta dimensión. En la agrupación K-Means, utilizar la distancia Manhattan en lugar de la distancia euclídea puede producir mejores resultados, sobre todo cuando se trata de datos dispersos de alta dimensión o cuando hay valores atípicos. Además, suele preferirse en la clasificación de textos y la agrupación de documentos debido a su eficacia con los espacios vectoriales dispersos. La menor sensibilidad de la distancia Manhattan a los valores extremos en dimensiones individuales puede dar lugar a resultados de agrupación más equilibrados en determinados conjuntos de datos.

Reconocimiento de imágenes 

La distancia Manhattan puede utilizarse para comparar valores de píxeles o vectores de características. Es especialmente útil en la concordancia de plantillas, cuando intentas encontrar apariciones de una imagen pequeña dentro de otra más grande. También es valiosa en los sistemas de reconocimiento facial, detección de objetos en secuencias de vídeo, o coincidencia de patrones en grandes bases de datos de imágenes, donde la velocidad es crucial, y la ligera pérdida de precisión en comparación con la distancia euclidiana suele ser insignificante.

Detección de valores atípicos 

La distancia Manhattan puede utilizarse para identificar puntos de datos que son significativamente diferentes de otros en un conjunto de datos, porque es menos sensible a los valores extremos en dimensiones individuales en comparación con la distancia euclídea. Esta propiedad la hace útil en sistemas de detección de anomalías, como los utilizados en la detección de fraudes o la seguridad de redes. En los sistemas financieros, por ejemplo, la distancia Manhattan puede ayudar a identificar patrones de transacciones inusuales sin dejarse influir demasiado por los valores extremos de un único atributo, lo que puede conducir a menos errores.

Sistemas de Información Geográfica (SIG) 

En aplicaciones SIG, la distancia Manhattan puede modelar el movimiento a lo largo de una red de calles en forma de cuadrícula, lo que la hace útil para la planificación urbana y la logística. Se utiliza en problemas de asignación de emplazamientos, como la determinación de ubicaciones óptimas para instalaciones basadas en la minimización de la distancia total de desplazamiento en una ciudad. La distancia Manhattan también puede aplicarse en tareas de análisis espacial, como la creación de zonas tampón alrededor de elementos lineales como carreteras o ríos. Los urbanistas podrían utilizar la distancia Manhattan para analizar la accesibilidad de los servicios públicos, mientras que las empresas de logística podrían emplearla para optimizar las rutas de reparto en las ciudades.

Propiedades matemáticas de la distancia Manhattan

La distancia Manhattan posee varias propiedades matemáticas importantes que la hacen especialmente útil. Exploremos dos aspectos clave: sus propiedades de espacio métrico y su robustez frente a los valores atípicos.

Propiedades del espacio métrico

La distancia Manhattan es una métrica verdadera, lo que significa que satisface las cuatro condiciones requeridas para una función de distancia en un espacio métrico:

1. No negatividad: La distancia entre dos puntos cualesquiera es siempre no negativa. d(x, y) ≥ 0 para todas las x e y.
2. Identidad de los indiscernibles: La distancia entre un punto y él mismo es cero, y si la distancia entre dos puntos es cero, son el mismo punto. d(x, y) = 0 si y sólo si x = y.
3. Simetría: La distancia del punto A al punto B es la misma que la distancia de B a A. d(x, y) = d(y, x) para todo x e y.
4. Desigualdad triangular: La distancia entre dos puntos es siempre menor o igual que la suma de las distancias entre esos puntos y un tercer punto. d(x, z) ≤ d(x, y) + d(y, z) para todas las x, y y z.

A diferencia de la distancia coseno, que no satisface la desigualdad del triángulo, la adherencia de la distancia Manhattan a todas estas propiedades la hace útil en diversas aplicaciones matemáticas y computacionales. Por ejemplo:

• En los algoritmos de optimización, la desigualdad triangular puede utilizarse para podar espacios de búsqueda de forma eficaz.
• En estructuras de datos como los árboles métricos, estas propiedades permiten búsquedas más rápidas del vecino más próximo.
• En el aprendizaje automático, los algoritmos que se basan en métricas de distancia (como k-vecinos más cercanos) pueden aprovechar estas propiedades para obtener garantías teóricas e implementaciones eficientes.

Discriminación mejorada de valores atípicos 

La distancia Manhattan, con su enfoque de suma lineal, suele proporcionar una mayor discriminación de los valores atípicos en comparación con la distancia euclidiana, que eleva las diferencias al cuadrado. Esta distinción surge porque la distancia Manhattan acumula las diferencias absolutas en cada dimensión de forma independiente, reduciendo la influencia abrumadora de las grandes discrepancias en una sola dimensión.

Considera dos puntos en un espacio 2D: A(0, 0) y B(10, 0). Ahora introduzcamos un punto atípico C con coordenadas (0, 100):

• Distancia Manhattan entre A y C: |0 - 0| + |0 - 100| = 100
• Distancia euclidiana entre A y C: √((0 - 0^)² + (0 - 100^)²) = 100
• Distancia Manhattan entre B y C: |10 - 0| + |0 - 100| = 110
• Distancia euclidiana entre B y C: √((10 - 0^)² + (0 - 100^)²) ≈ 100,5

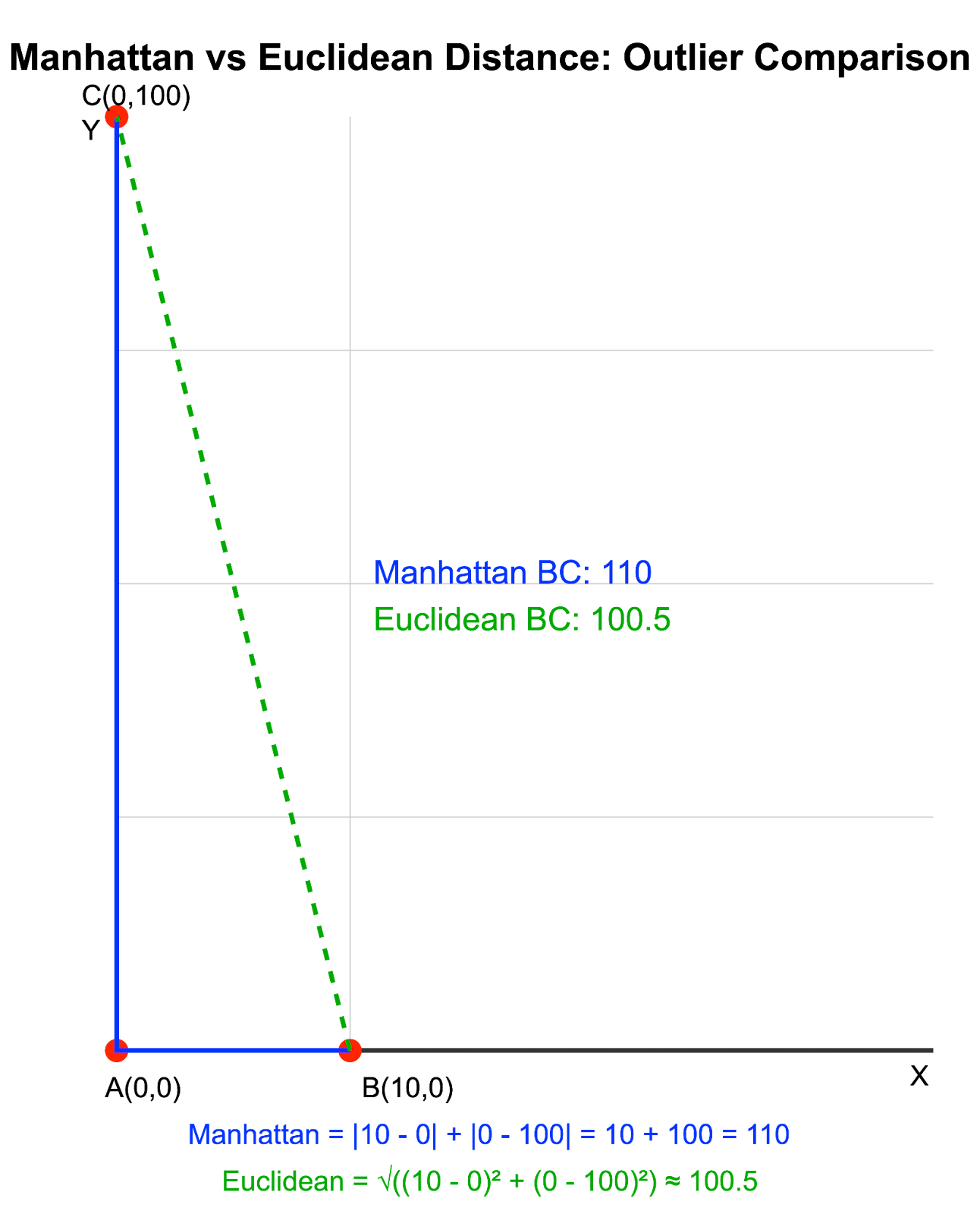Ilustración vs Euclídea Distancia Manhattan vs Euclídea con valores atípicos. Imagen del autor

En este ejemplo, la distancia Manhattan distingue claramente entre las distancias AC y BC, mientras que la distancia euclídea las muestra casi iguales debido al efecto dominante del valor atípico en la coordenada y.

Esta propiedad hace que la distancia de Manhattan sea especialmente útil en:

1. Espacios de alta dimensión en los que son frecuentes los valores atípicos, como en el tratamiento de imágenes o el análisis de textos.
2. Algoritmos de agrupación en los que quieras reducir el impacto de los valores atípicos en los centroides de los conglomerados.
3. Sistemas de detección de anomalías en los que quieras identificar valores atípicos sin inflar demasiado su importancia.

Al ser menos sensible a los valores extremos en dimensiones individuales, la distancia Manhattan puede proporcionar una medida más equilibrada de la disimilitud en muchos conjuntos de datos del mundo real, especialmente en aquellos con datos ruidosos o imperfectos.

Distancia Manhattan en Python y R

Aquí exploraremos cómo calcular la distancia Manhattan utilizando Python y R. Cada ejemplo mostrará diferentes enfoques, desde funciones personalizadas hasta métodos de biblioteca.

Ejemplos en Python

Python ofrece varias formas de calcular la distancia Manhattan. Exploremos dos métodos diferentes.

1. Cálculo mediante matrices NumPy:

import numpy as np
point_a_np = np.array([1, 1, 1])
point_b_np = np.array([4, 5, 6])
distance_numpy = np.sum(np.abs(point_a_np - point_b_np))
print(f"Manhattan distance (NumPy): {distance_numpy}")

Salida: 

Manhattan distance (NumPy): 12

Este método utiliza directamente matrices NumPy, lo que puede ser muy eficaz, sobre todo cuando se trata de grandes conjuntos de datos o cuando ya trabajas con matrices NumPy en tus análisis.

2. Cálculo mediante la función cityblock() de SciPy: 

from scipy.spatial.distance import cityblock
point_a = (1, 1, 1)
point_b = (4, 5, 6)
distance_scipy = cityblock(point_a, point_b)
print(f"Manhattan distance (SciPy): {distance_scipy}")

Salida:

Manhattan distance (SciPy): 12

SciPy proporciona la función cityblock(), que calcula la distancia Manhattan. Este método es sencillo y eficaz, sobre todo si trabajas con SciPy en tu proyecto. 

Ejemplos de R

R también proporciona múltiples formas de calcular la distancia de Manhattan. Examinemos dos enfoques diferentes.

1. Crear una función personalizada

manhattan_distance <- function(x1, y1, x2, y2) {
  abs(x1 - x2) + abs(y1 - y2)
}
# Example points 
point1 <- c(3, 5) # (x1, y1) 
point2 <- c(1, 9) # (x2, y2) 
# Calculate Manhattan distance between point1 and point2 
distance <- manhattan_distance(point1[1], point1[2], point2[1], point2[2]) 
print(paste("Manhattan distance (custom function):", distance))

Salida:

"Manhattan distance (custom function): 6"

En este ejemplo, creamos una función personalizada llamada manhattan_distance. Esta función toma las coordenadas de dos puntos como entradas y halla la distancia Manhattan sumando las diferencias absolutas de sus respectivas coordenadas.

2. Utilizar la biblioteca de estadísticas

point_a <- c(1, 1, 1)
point_b <- c(4, 5, 6)
distance_builtin <- stats::dist(rbind(point_a, point_b), method = "manhattan")
print(paste("Manhattan distance:", distance_builtin))

Salida: 

"Manhattan distance: 12"

En el segundo ejemplo, utilizamos la función dist() del paquete stats para calcular la distancia Manhattan. Este enfoque es útil cuando se trata de matrices o puntos múltiples, ya que simplifica el proceso considerablemente.

Conclusión

La importancia de la distancia Manhattan radica en su sencillez, eficiencia computacional y robustez frente a valores atípicos en determinados escenarios. A diferencia de la distancia euclidiana, la distancia Manhattan suele proporcionar resultados más intuitivos en los sistemas basados en cuadrículas y puede ser más eficiente de calcular, especialmente en espacios de alta dimensión. 

Es más, la distancia Manhattan y otras métricas de distancia aparecen en una gran variedad de lugares. Además de nuestro curso Diseño de flujos de trabajo de aprendizaje automático en Python, que incluye un capítulo sobre aprendizaje basado en la distancia, y el curso Análisis de conglomerados en R, que utiliza métricas basadas en la distancia para la clasificación y la reducción dimensional, también puedes consultar nuestro curso Detección de anomalías en Python, que utiliza métricas de distancia para la detección de valores atípicos y el escalado de características.  

Recuerda que la elección de la métrica de distancia puede influir significativamente en el rendimiento y los resultados de tus algoritmos. Si sabes cuándo y cómo utilizar la distancia Manhattan, estarás añadiendo una poderosa herramienta a tu caja de herramientas de la ciencia de datos. ¡Sigue experimentando, aprendiendo y ampliando los límites de lo que es posible con los algoritmos basados en la distancia!