Distance de Minkowski : Un guide complet

Les mesures de distance constituent l'épine dorsale de nombreux algorithmes dans le domaine de la science des données et de l'apprentissage automatique, car elles permettent de mesurer la similarité ou la dissemblance entre des points de données. Dans ce guide, nous allons explorer les fondements de la distance de Minkowski, ses propriétés mathématiques et ses implémentations. Nous examinerons ses liens avec d'autres mesures de distance courantes et démontrerons son utilisation à l'aide d'exemples de codage en Python et en R. 

Que vous développiez des algorithmes de regroupement, que vous travailliez sur la détection d'anomalies ou que vous peaufiniez des modèles de classification, la compréhension de la distance de Minkowski peut améliorer votre approche de l'analyse des données et du développement de modèles. Jetons un coup d'œil.

Qu'est-ce que la distance de Minkowski ?

La distance de Minkowski est une métrique polyvalente utilisée dans les espaces vectoriels normés, nommée d'après le mathématicien allemand Hermann Minkowski. Il s'agit d'une généralisation de plusieurs mesures de distance bien connues, ce qui en fait un concept fondamental dans divers domaines tels que les mathématiques, l'informatique et l'analyse de données.

À la base, la distance de Minkowski permet de mesurer la distance entre deux points dans un espace multidimensionnel. Ce qui la rend particulièrement utile, c'est sa capacité à englober d'autres mesures de distance en tant que cas particuliers, principalement par le biais d'un paramètre p. Ce paramètre permet à la distance de Minkowski de s'adapter à différents espaces de problèmes et caractéristiques de données. La formule générale de la distance de Minkowski est la suivante :

Où ?

• x et y sont deux points dans un espace à n dimensions

• p est un paramètre qui détermine le type de distance (p ≥ 1)

• |xi - yi| représente la différence absolue entre les coordonnées x et y dans chaque dimension

La distance de Minkowski est utile pour deux raisons principales. D'une part, il vous permet d'alterner entre la distance de Manhattan et la distance euclidienne en fonction des besoins. Deuxièmement, elle reconnaît que tous les ensembles de données (pensez aux espaces à haute dimension) ne sont pas adaptés à la distance purement manhattanienne ou purement euclidienne.

Dans la pratique, le paramètre p est généralement choisi en incorporant un processus de validation train/test. En testant différentes valeurs de p au cours de la validation croisée, vous pouvez déterminer la valeur qui fournit les meilleures performances du modèle pour votre ensemble de données spécifique.

Comment fonctionne la distance de Minkowski

Voyons comment la distance de Minkowski se situe par rapport aux autres formules de distance, puis prenons un exemple. 

Généralisation d'autres mesures de distance

La première chose à considérer est la façon dont la formule de la distance de Minkowski contient les formules des distances de Manhattan, d'Euclide et de Chebyshev. 

Distance de Manhattan (p = 1) : 

Lorsque p est fixé à 1, la distance de Minkowski devient la distance de Manhattan. 

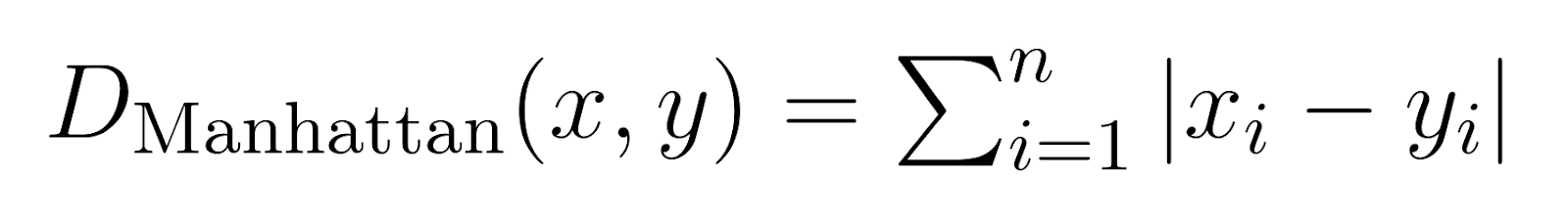
Également connue sous le nom de distance entre les pâtés de maisons ou de norme L1, la distance de Manhattan mesure la somme des différences absolues. 

Distance euclidienne (p = 2) : 

Lorsque p est fixé à 2, la distance de Minkowski devient une distance euclidienne.

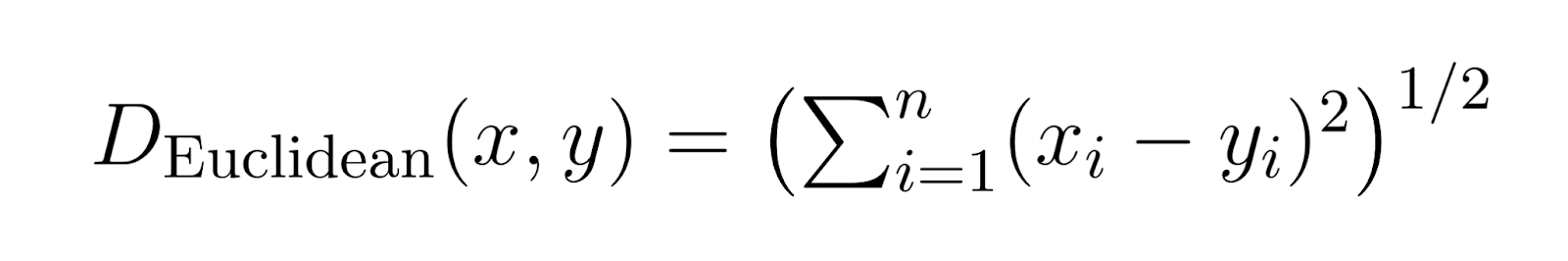
La distance euclidienne est la mesure de distance la plus courante. Elle représente la distance en ligne droite entre deux points. 

Distance de Chebyshev (p → ∞) : 

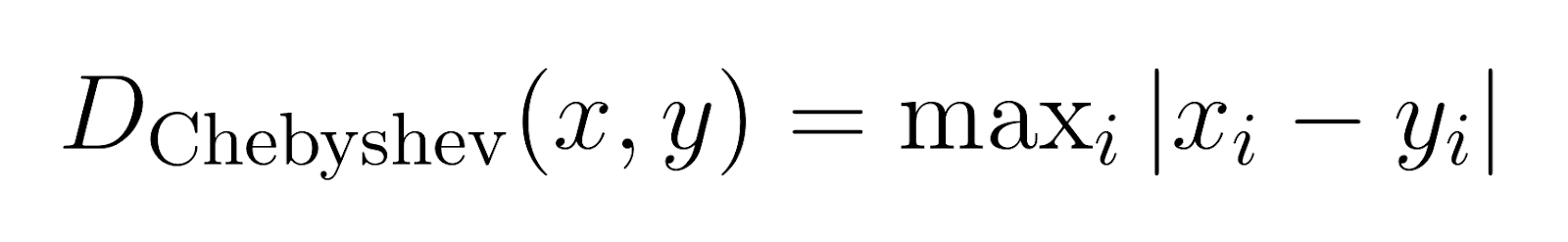
La distance de Chebyshev, également connue sous le nom de distance d'échiquier, mesure la différence maximale le long d'une dimension. 

Travailler à partir d'un exemple

Pour bien comprendre la fonctionnalité et la puissance de la distance de Minkowski, prenons un exemple. Cette exploration nous aidera à comprendre comment le paramètre p affecte le calcul et l'interprétation des distances dans les espaces multidimensionnels.

Considérons deux points dans un espace 2D :

• Point A : (2, 3)
• Point B : (5, 7)

Nous allons calculer la distance de Minkowski entre ces points pour différentes valeurs de p.

Le paramètre p dans la formule de la distance de Minkowski contrôle la sensibilité de la métrique aux différences entre les composants individuels :

• Lorsque p=1: Toutes les différences contribuent de manière linéaire.
• Lorsque p=2: Les différences plus importantes ont un impact plus significatif en raison de la mise au carré.
• Lorsque p>2: L'accent est mis sur les différences les plus importantes.
• Lorsque p→∞ : Seule la différence maximale entre toutes les dimensions compte.

Lorsque p augmente, la distance de Minkowski diminue généralement et se rapproche de la distance de Tchebychev. En effet, les valeurs élevées de p donnent plus de poids à la plus grande différence et moins aux plus petites.

Pour visualiser comment différentes valeurs de p affectent le calcul de la distance entre nos points A(2, 3) et B(5, 7), examinons le graphique suivant :

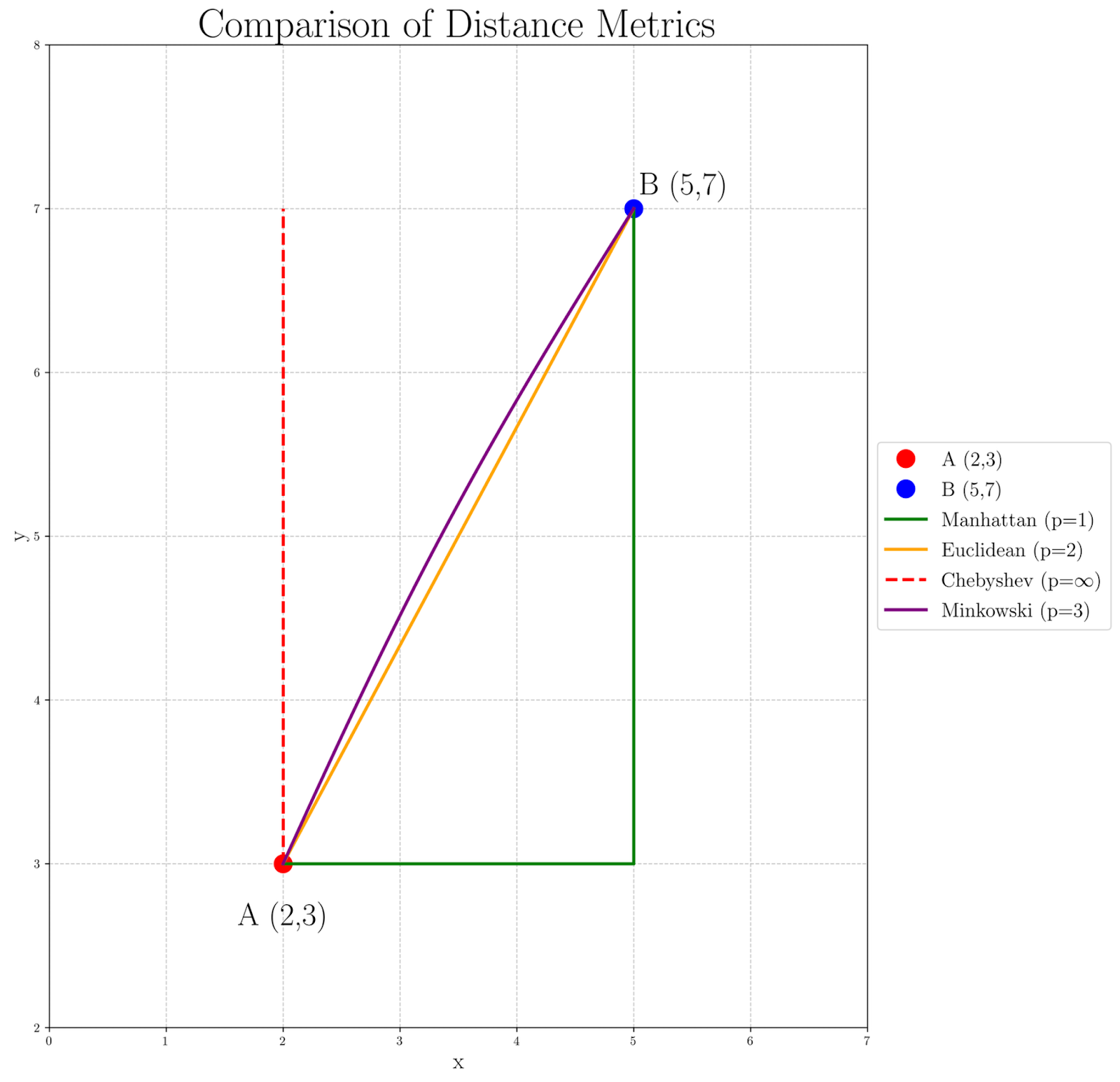
En observant le graphique, nous pouvons voir comment la mesure de la distance change lorsque p augmente :

• La distance de Manhattan (p=1), représentée par le chemin vert, donne le chemin le plus long, car il suit strictement la grille.
• La distance euclidienne (p=2), représentée par la ligne droite orange, indique un chemin direct, en ligne droite.
• La distance de Chebyshev (p=∞), représentée par les lignes pointillées rouges, se concentre uniquement sur la plus grande différence de coordonnées, créant un chemin qui se déplace au maximum dans une dimension avant d'aborder l'autre.
• La distance de Minkowski avec p=3 en violet présente une légère courbe, indiquant la transition entre les distances euclidienne et de Chebyshev.

Cette visualisation nous aide à comprendre pourquoi différentes valeurs de p peuvent être choisies pour diverses applications. Par exemple, la distance de Manhattan peut être plus appropriée pour les problèmes de navigation urbaine, alors que la distance euclidienne est souvent utilisée dans les calculs d'espace physique. Des valeurs plus élevées de p, comme dans le cas de Minkowski p=3, peuvent être utiles dans les scénarios où des différences plus importantes doivent être soulignées, et la distance de Chebyshev peut être préférée lorsque la différence maximale dans n'importe quelle dimension est le facteur le plus critique.

Applications de la distance de Minkowski

La distance de Minkowski, avec son paramètre ajustable p, est un outil flexible utilisé dans différents domaines. En modifiant p, nous pouvons adapter la façon dont nous mesurons la distance entre les points, ce qui permet de l'adapter à différentes tâches. Vous trouverez ci-dessous quatre applications dans lesquelles la distance de Minkowski joue un rôle important.

Apprentissage automatique et science des données

Dans l'apprentissage automatique et la science des données, la distance de Minkowski est fondamentale pour les algorithmes qui reposent sur la mesure de la similarité ou de la dissimilarité entre les points de données. L'algorithme des k-voisins les plus proches (k-NN), qui classe les points de données en fonction des catégories de leurs voisins les plus proches, en est un exemple frappant. En utilisant la distance de Minkowski, nous pouvons ajuster le paramètre p pour modifier la façon dont nous calculons la "proximité" entre les points.

Reconnaissance des formes

La reconnaissance des formes consiste à identifier des formes et des régularités dans les données, comme la reconnaissance de l'écriture manuscrite ou la détection des traits du visage. Dans ce contexte, la distance de Minkowski mesure la différence entre les vecteurs de caractéristiques représentant des modèles. Par exemple, dans la reconnaissance d'images, chaque image peut être représentée par un vecteur de valeurs de pixels. Le calcul de la distance de Minkowski entre ces vecteurs permet de quantifier le degré de similitude ou de différence des images.

En ajustant p, nous pouvons contrôler la sensibilité de la mesure de distance aux différences de caractéristiques spécifiques. Une valeur inférieure à p peut prendre en compte les différences globales entre tous les pixels, tandis qu'une valeur supérieure à p peut mettre l'accent sur des différences significatives dans certaines régions de l'image.

Détection des anomalies

La détection des anomalies vise à identifier les points de données qui s'écartent de manière significative de la majorité, ce qui est crucial dans des domaines tels que la détection des fraudes, la sécurité des réseaux et la détection des défaillances dans les systèmes. La distance de Minkowski est utilisée pour mesurer la distance entre un point de données et d'autres dans l'ensemble de données. Les points présentant de grandes distances sont des anomalies potentielles. En choisissant une adresse p appropriée, les analystes peuvent améliorer la sensibilité des systèmes de détection des anomalies aux types d'écarts les plus pertinents dans leur contexte spécifique.

Géométrie informatique et analyse spatiale

En géométrie informatique et en analyse spatiale, la distance de Minkowski est utilisée pour calculer les distances entre les points dans l'espace, ce qui constitue la base de nombreux algorithmes géométriques. Par exemple, la détection des collisions dans ces domaines repose sur la distance de Minkowski pour déterminer si les objets sont suffisamment proches pour interagir. En ajustant p, les développeurs peuvent créer diverses limites de collision, allant de l'angulaire ( p inférieur) à l'arrondi ( p supérieur).

Au-delà de la détection des collisions, la distance de Minkowski peut être utile pour le regroupement spatial et l'analyse des formes. La variation de la valeur de p permet aux chercheurs de mettre l'accent sur différents aspects des relations spatiales, qu'il s'agisse des distances entre les pâtés de maisons ou des similitudes de formes globales.

Propriétés mathématiques de la distance de Minkowski

La distance de Minkowski est non seulement un outil polyvalent dans les applications pratiques, mais aussi un concept important en théorie mathématique, en particulier dans l'étude des espaces métriques et des normes.

Propriétés de l'espace métrique

La distance de Minkowski satisfait aux quatre propriétés essentielles requises pour qu'une fonction soit considérée comme une métrique dans un espace métrique :

• Non-négativité: La distance de Minkowski entre deux points quelconques est toujours non négative, d(x,y)≥0. Ceci est évident puisqu'il s'agit de la racine p-ième d'une somme de termes non négatifs (valeurs absolues élevées à la puissance p).
• Identité des indiscernables: La distance de Minkowski entre deux points est nulle si et seulement si les deux points sont identiques. Mathématiquement, d(x,y) = 0 si et seulement si x=y. Cela s'explique par le fait que la différence absolue entre des composants identiques est nulle.
• Symétrie: La distance de Minkowski est symétrique, ce qui signifie que d(x,y)=d(y,x). Cette propriété est valable parce que l'ordre de soustraction dans les termes en valeur absolue n'affecte pas le résultat.
• Inégalité des triangles: La distance de Minkowski satisfait à l'inégalité triangulaire, qui stipule que pour trois points x, y et z, la distance de x à z est au maximum la somme des distances de x à y et de y à z ; formellement, d(x,z)≤d(x,y)+d(y,z). Cette propriété est moins intuitive à prouver directement à partir de la formule et nécessite généralement des mathématiques plus avancées, mais elle garantit essentiellement que le chemin direct entre deux points est le plus court.

Généralisation des normes

La distance de Minkowski sert de cadre général qui unifie les différentes façons de mesurer les distances dans les espaces mathématiques grâce au concept de normes. En termes simples, unenorme est une fonction qui attribue une longueur ou une taille non négative à un vecteur dans un espace vectoriel, mesurant essentiellement la "longueur" du vecteur. En ajustant le paramètre p dans la formule de la distance de Minkowski, nous pouvons passer en douceur d'une norme à l'autre, chacune fournissant une méthode unique de calcul de la longueur des vecteurs.

Par exemple, lorsque p=1, la distance de Minkowski devient la norme de Manhattan, qui mesure la distance comme la somme des différences absolues le long de chaque dimension - imaginez que vous naviguez dans une grille de rues de la ville. Avec p=2, elle devient lanorme euclidienne , qui calcule la distance en ligne droite ("à vol d'oiseau") entre les points. Lorsque p s'approche de l'infini, elle converge vers lanorme de Chebyshev , où la distance est déterminée par la plus grande différence entre les dimensions. Cette flexibilité permet à la distance de Minkowski de s'adapter à divers contextes mathématiques et pratiques, ce qui en fait un outil polyvalent pour mesurer les distances dans différents scénarios.

Calcul de la distance de Minkowski en Python et R

Explorons les implémentations des calculs de distance de Minkowski en utilisant à la fois Python et R. Nous examinerons des packages et des bibliothèques facilement disponibles qui permettent d'atteindre cet objectif. 

Exemple en Python

Pour calculer la distance de Minkowski en Python, nous pouvons utiliser la bibliothèque SciPy, qui fournit des implémentations efficaces de diverses métriques de distance. Voici un exemple qui calcule la distance de Minkowski pour différentes valeurs de p :

import numpy as np
from scipy.spatial import distance

# Example points
point_a = [2, 3]
point_b = [5, 7]

# Different p values
p_values = [1, 2, 3, 10, np.inf]
print("Minkowski distances using SciPy:")

for p in p_values:
	if np.isinf(p):
	    # For p = infinity, use Chebyshev distance
	    dist = distance.chebyshev(point_a, point_b)
	    print(f"p = ∞, Distance = {dist:.2f}")
	else:
	        dist = distance.minkowski(point_a, point_b, p)
	        print(f"p = {p}, Distance = {dist:.2f}")

En exécutant ce code, les lecteurs peuvent observer comment la distance change avec différentes valeurs de p, renforçant ainsi les concepts discutés plus tôt dans l'article.

Minkowski distances using SciPy:
p = 1, Distance = 7.00
p = 2, Distance = 5.00
p = 3, Distance = 4.50
p = 10, Distance = 4.02
p = ∞, Distance = 4.00

Ce code démontre :

1. Comment utiliser les fonctions de distance de SciPy pour les distances de Minkowski et de Chebyshev.
2. Calcul des distances pour différentes valeurs de p, y compris l'infini.
3. La relation entre la distance de Minkowski et d'autres métriques (Manhattan, Euclide, Chebyshev).

Exemple R

Pour R, nous utiliserons la fonction dist() de la bibliothèque stats:

# Define the Minkowski distance function using stats::dist

minkowski_distance <- function(x, y, p) {
  points <- rbind(x, y)
  if (is.infinite(p)) {
    # For p = Inf, use method = "maximum" for Chebyshev distance
    distance <- stats::dist(points, method = "maximum")
  } else {
    distance <- stats::dist(points, method = "minkowski", p = p)
  }
  return(as.numeric(distance))
}

# Example usage
point_a <- c(2, 3)
point_b <- c(5, 7)

# Different p values
p_values <- c(1, 2, 3, 10, Inf)
cat("Minkowski distances between points A and B using stats::dist:\n")

for (p in p_values) {
  distance <- minkowski_distance(point_a, point_b, p)
  if (is.infinite(p)) {
    cat(sprintf("p = ∞, Distance = %.2f\n", distance))
  } else {
    cat(sprintf("p = %g, Distance = %.2f\n", p, distance))
  }
}

Ce code démontre :

1. Comment créer une fonction minkowski_distance en utilisant la fonction dist() à partir de stats.

2. Traitement de différentes valeurs de p, y compris l'infini pour la distance de Chebyshev.

3. Calcul de la distance de Minkowski pour différentes valeurs de p.

4. Formatage de la sortie pour afficher les distances arrondies à 2 décimales.

Le résultat de ce code sera le suivant :

Minkowski distances between points A and B using stats::dist:
p = 1, Distance = 7.00
p = 2, Distance = 5.00
p = 3, Distance = 4.50
p = 10, Distance = 4.02
p = ∞, Distance = 4.00

Cette implémentation R fournit un pendant à l'exemple Python, permettant aux lecteurs de voir comment la distance de Minkowski peut être calculée dans différents environnements de programmation.

Conclusion

La distance de Minkowski offre une approche souple et adaptable pour mesurer les distances dans les espaces multidimensionnels. Sa capacité à généraliser d'autres mesures de distance courantes grâce au paramètre p en fait un outil précieux dans divers domaines de la science des données et de l'apprentissage automatique. En ajustant p, les praticiens peuvent adapter leurs calculs de distance aux caractéristiques spécifiques de leurs données et aux exigences de leurs projets, ce qui peut améliorer les résultats dans des tâches allant du regroupement à la détection d'anomalies.

Lorsque vous appliquerez la distance de Minkowski dans votre propre travail, nous vous encourageons à expérimenter différentes valeurs de p et à observer leur impact sur vos résultats. Pour ceux qui cherchent à approfondir leur compréhension et leurs compétences, nous vous recommandons d'explorer le cours Designing Machine Learning Workflows in Python et d'envisager notre programme de carrière Data Scientist Certification. Ces ressources peuvent vous aider à approfondir votre connaissance des mesures de distance et à les appliquer efficacement dans divers scénarios.