Curso
Los métodos Monte Carlo, que originalmente recibieron su nombre del Casino Monte Carlo de Mónaco, se utilizan ampliamente en campos como las finanzas, la ingeniería, la cadena de suministro y la ciencia para modelar fenómenos con una incertidumbre significativa en sus datos de entrada.
Pero, ¿qué es la simulación de Monte Carlo? ¿Cómo funciona? ¿Y cómo puedes implementar la simulación y analizar los resultados?
Este tutorial te presentará la simulación de Monte Carlo y los conceptos estadísticos relevantes que subyacen a esta técnica. También implementaremos la simulación de Monte Carlo en Excel, familiarizándote con las funciones integradas relevantes de Excel.
Por último, el tutorial te proporcionará las mejores prácticas, técnicas avanzadas y recursos adicionales, lo que lo convierte en tu guía completa para aprender todo lo que necesitas saber sobre la simulación de Monte Carlo en Microsoft Excel.
¿Qué es la simulación de Monte Carlo?
La simulación de Monte Carlo es una técnica matemática utilizada para modelar la probabilidad de diferentes resultados en un proceso que no se puede predecir fácilmente debido a la intervención de variables aleatorias.
Es una herramienta poderosa para comprender el impacto del riesgo y la incertidumbre en diversos campos. El método se basa en muestreos aleatorios repetidos para simular el comportamiento de sistemas y procesos complejos.
El problema se modela primero mediante una distribución de probabilidad para cada variable que tiene una incertidumbre inherente. A continuación, se extraen grandes cantidades de muestras aleatorias de estas distribuciones de probabilidad, y estas muestras se utilizan para calcular los resultados. Este proceso se repite muchas veces para crear una distribución de posibles resultados, que se puede analizar estadísticamente para proporcionar predicciones sobre cómo se comportará un sistema.
En pocas palabras. La simulación de Monte Carlo es una técnica que predice cómo se comportarán los sistemas complejos simulando sus resultados muchas veces utilizando valores aleatorios. Se siguen varios pasos:
- Incertidumbre del modelo: Define cómo puede variar cada variable utilizando distribuciones de probabilidad.
- Muestreo aleatorio: Selecciona valores aleatoriamente para estas variables basándote en sus distribuciones.
- Simular resultados: Utiliza estos valores para simular el comportamiento del sistema.
- Analizar los resultados: Repite el proceso muchas veces para obtener una variedad de resultados posibles y, a continuación, analízalos para predecir los escenarios más probables.
A continuación, desarrollaremos nuestros conocimientos básicos sobre la simulación de Monte Carlo profundizando en algunos conceptos estadísticos relevantes.
Variables aleatorias y distribuciones de Monte Carlo
Las variables aleatorias y sus distribuciones de probabilidad asociadas son fundamentales para la simulación de Monte Carlo, ya que proporcionan el marco matemático para modelar y simular la aleatoriedad y la variabilidad inherentes a los sistemas complejos.
Variables aleatorias
Una variable aleatoria es una variable cuyos valores son resultados de un fenómeno aleatorio.
Las variables aleatorias se clasifican en dos tipos:
- Variables aleatorias discretas: Estas variables toman un número contable de valores distintos. En las simulaciones, las variables discretas pueden modelar escenarios como el número de artículos defectuosos en un lote, las llegadas de clientes por hora u otros eventos contables.
- Variables aleatorias continuas: Estas variables pueden adoptar cualquier valor dentro de un rango continuo. Las variables continuas se utilizan para simulaciones relacionadas con mediciones físicas o duraciones temporales.
Las variables aleatorias se utilizan en simulaciones porque contienen la incertidumbre que las técnicas de Monte Carlo están diseñadas para explorar y cuantificar.
Distribuciones de probabilidad
Las distribuciones de probabilidad describen cómo se distribuyen las probabilidades entre los valores de una variable aleatoria.
Las distribuciones de probabilidad se utilizan en la simulación de Monte Carlo para definir cómo se espera que se comporten diferentes entradas o escenarios, lo cual es esencial para realizar modelos precisos y tomar decisiones acertadas.
La distribución normal es la distribución más utilizada en estadística y simulaciones, ya que muchos fenómenos naturales y artificiales tienden a seguir esta distribución debido al teorema del límite central.
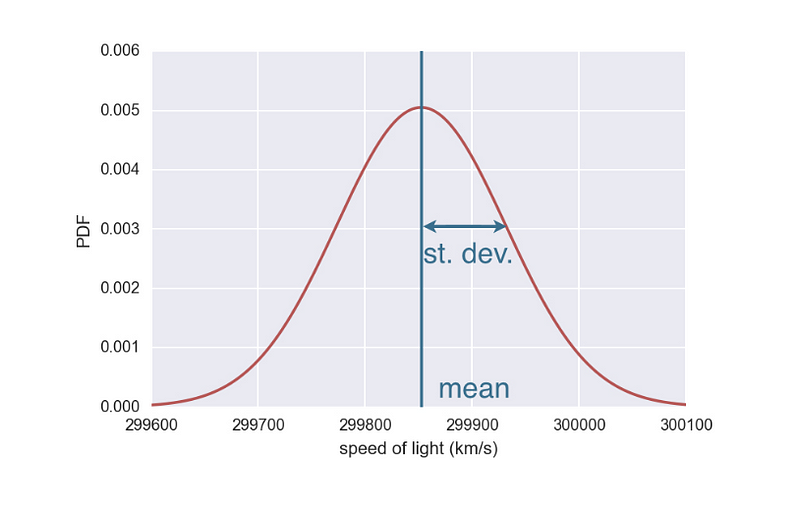
Distribución normal (Fuente)
La distribución normal se utiliza para modelar variables que están influenciadas por muchos efectos pequeños e independientes, como los errores de medición o los rendimientos del mercado bursátil.
Otras distribuciones de probabilidad son las distribuciones uniformes, que se utilizan cuando cualquier resultado dentro de un rango específico tiene la misma probabilidad, una suposición habitual en las simulaciones cuando no se dispone de datos previos, y las distribuciones binomiales, que se utilizan para modelar escenarios con dos resultados posibles (éxito/fracaso) en una serie de experimentos, como pruebas de aprobado/suspenso o controles de calidad.
Ahora que hemos comprendido los conceptos y la teoría que hay detrás de las simulaciones de Monte Carlo, pasemos a la parte práctica de su implementación.
Aprende los fundamentos de Excel
¿Por qué utilizar Excel para la simulación de Monte Carlo?
Una vez que hayas decidido implementar una simulación de Monte Carlo, dispones de múltiples herramientas, como Excel, Python, R, SAS y MATLAB, que te ayudarán con las simulaciones.
El factor más importante a tener en cuenta, especialmente cuando se implementa la simulación de Monte Carlo por primera vez, es tu familiaridad general con la herramienta. Excel es una de las herramientas más utilizadas en el mundo empresarial, lo que significa que muchas personas ya están familiarizadas con sus operaciones básicas. Esto reduce el tiempo de formación y elimina la necesidad de aprender a utilizar un nuevo software desde cero.
Excel también ofrece herramientas fáciles de usar para crear tablas y gráficos, que pueden resultar útiles para visualizar los resultados de las simulaciones. Además, hay varios complementos potentes disponibles para Excel, que mejoran su capacidad para realizar simulaciones complejas de Monte Carlo.
Sin embargo, también cabe señalar que para simulaciones más avanzadas, especialmente aquellas que requieren manejar grandes conjuntos de datos o ejecutar un número muy elevado de simulaciones, puede ser más adecuado utilizar herramientas más especializadas que Excel.
Funciones clave de Excel para Monte Carlo
A continuación, exploraremos dos funciones esenciales de Excel: RAND() y NORM.INV(), cubriendo su sintaxis, parámetros y casos de uso típicos. Estas funciones ayudan a generar números aleatorios y definir distribuciones de probabilidad, que son aspectos fundamentales de cualquier simulación.
La función RAND()
RAND() genera un número aleatorio mayor o igual a 0 y menor que 1. Los números están distribuidos uniformemente, lo que significa que cualquier número dentro del rango especificado tiene la misma probabilidad de aparecer.
La sintaxis de RAND() es la siguiente:
RAND()La función RAND() no requiere ningún argumento. Se utiliza simplemente como RAND().
En el contexto de la simulación de Monte Carlo, RAND() se puede utilizar para simular la ocurrencia de eventos aleatorios o para variar las entradas en tu modelo.
La función NORM.INV()
Mientras que RAND() genera números aleatorios uniformes, NORM.INV() se utiliza para generar números aleatorios a partir de una distribución normal, lo cual es un requisito habitual en una simulación de Monte Carlo. Esta función devuelve la inversa de la distribución acumulativa normal para una media y una desviación estándar especificadas.
La sintaxis de la función « NORM.INV() » es la siguiente:
NORM.INV(probability, mean, standard_deviation)Los parámetros son:
-
probability: Probabilidad correspondiente a la distribución normal, que debe ser un valor entre 0 y 1. Esto suele generarse mediante la funciónRAND(). -
mean: La media aritmética de la distribución normal. -
standard_deviation: La desviación estándar de la distribución normal, una medida de la dispersión de los números alrededor de la media.
La función « NORM.INV() » se utiliza para transformar números aleatorios distribuidos uniformemente de la función « RAND() » en números que siguen una distribución normal especificada. Esto resulta útil para modelar variables que se espera que muestren una variabilidad natural siguiendo una curva normal.
Ahora que ya tenemos todos los componentes básicos, funciones y conceptos que hay detrás de una simulación de Monte Carlo, vamos a implementar una en Microsoft Excel.
Implementación de la simulación de Monte Carlo en Microsoft Excel: Un ejemplo
Imagina que eres analista de datos en una dinámica empresa de electrónica de consumo y te han encargado evaluar la viabilidad financiera del lanzamiento de un nuevo dispositivo wearable para el seguimiento de la actividad física.
El mercado de estos dispositivos es competitivo y la demanda de los consumidores puede ser muy variable, ya que se ve influida por las tendencias estacionales, la eficacia del marketing y las acciones de la competencia. Además, los costes asociados a la fabricación de estos dispositivos están sujetos a fluctuaciones debido a los cambios en los costes de los materiales y a las incertidumbres de la cadena de suministro.
Has decidido utilizar la simulación de Monte Carlo en Excel para abordar estos retos. Crees que este enfoque te ayudará a estimar la rentabilidad potencial en diferentes escenarios, lo que permitirá a la empresa tomar decisiones bien fundamentadas sobre estrategias de precios, volúmenes de producción e inversiones en marketing.
También has analizado datos históricos de lanzamientos de productos similares y estudios de mercado dentro del sector de la electrónica de consumo. A partir de este análisis, has llegado a ciertas conclusiones que servirán de base para tu simulación:
- Una demanda media de 10 000 unidades de nuevos dispositivos durante el primer año de lanzamiento, con una desviación estándar de 2000 unidades, lo que refleja la incertidumbre en la aceptación por parte de los consumidores.
- El precio de venta por unidad suele oscilar entre 50 y 70 dólares, dependiendo de los precios de la competencia y la saturación del mercado.
- El costo unitario, influenciado por la volatilidad de los precios de los materiales y la eficiencia de la fabricación, es de 30 dólares por unidad, con una desviación estándar de 5 dólares.
Estos datos históricos constituyen los supuestos subyacentes de los parámetros de simulación, lo que ayuda a crear una simulación que refleje con mayor precisión las condiciones actuales del mercado.
Los pasos que puedes seguir para implementar la simulación de Monte Carlo para este ejemplo concreto son los siguientes:
Paso 1: Configura tu hoja de Excel
En primer lugar, prepara tu hoja de cálculo de Excel para incluir columnas para cada variable y una columna para el beneficio calculado.
Así es como se vería inicialmente:
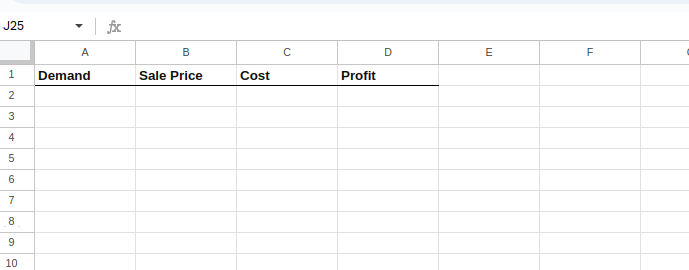
Configuración de la hoja de Excel.
Paso 2: Formulas de entrada para variables
En cada fila, introducirás fórmulas para generar valores aleatorios para la demanda, el precio de venta y el coste basándote en las distribuciones que hayas identificado:
- Demanda: Distribución normal (media = 10 000 unidades, desviación estándar = 2000 unidades)
- Precio de venta: Distribución uniforme (entre 50 y 70 dólares)
- Coste: Distribución normal (media = 30 $, desviación estándar = 5 $)
Para introducir estas fórmulas una por una, selecciona la celda A2 y escribe lo siguiente:
=NORM.INV(RAND(), 10000, 2000)La ecuación anterior crea una distribución normal con una media y una desviación estándar dadas, como se muestra a continuación:
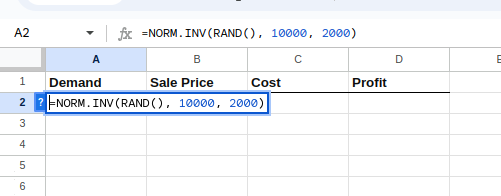
Creación de la distribución para la demanda.
A continuación, selecciona la celda B2 y escribe lo siguiente:
=50 + (70-50) * RAND()La ecuación anterior crea una distribución uniforme entre 50 y 70 dólares para el precio de venta, como se muestra a continuación:
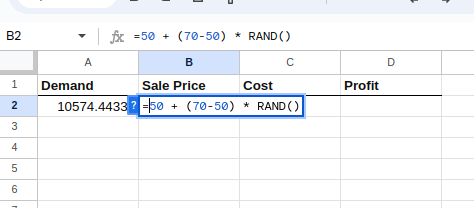
Creación de la distribución para el precio de venta.
Selecciona la celda C2 y escribe lo siguiente:
=NORM.INV(RAND(), 30, 5)La ecuación anterior, similar a la ecuación de la demanda, crea una distribución normal con una media y una desviación estándar dadas, como se muestra a continuación:
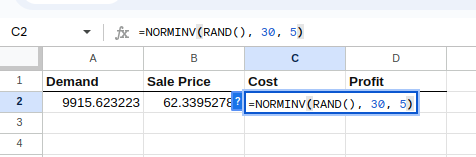
Creación de la distribución por coste.
Paso 3: Calcula la variable dependiente.
Ahora, calcula el beneficio, que es la variable dependiente, para cada simulación utilizando la fórmula de la columna D:
=(B2 - C2) * A2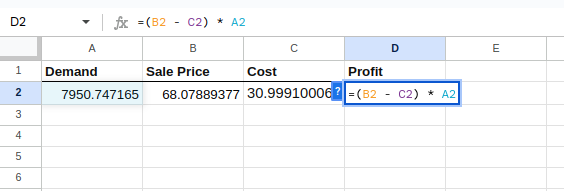
Cálculo de los beneficios.
Paso 4: Rellena para simular múltiples escenarios.
Lo que hemos hecho hasta ahora es crear una única simulación. Ampliémoslo a múltiples, digamos mil simulaciones.
Selecciona las celdas A2 a D2 y arrastra el controlador de relleno (un pequeño cuadrado situado en la parte inferior derecha de la selección) hacia abajo para rellenar las fórmulas en tantas filas como quieras simular (por ejemplo, 1000 filas para 1000 simulaciones).
Tendrá un aspecto similar a este:
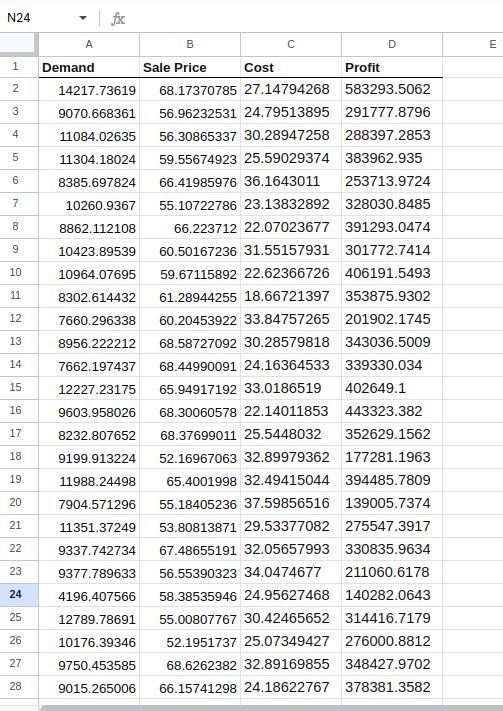
Creación de las simulaciones.
Paso 5: Analizar los resultados
Después de ejecutar las simulaciones, puedes analizar los resultados utilizando funciones estadísticas como mínimo, máximo, promedio y desviaciones estándar. No dudes en consultar rápidamente la hoja de referencia de Excel para refrescar tus conocimientos sobre las funciones integradas de Excel que utilizaremos a continuación.
Para calcular el beneficio medio previsto cada mes, escribe lo siguiente en una celda, por ejemplo, G6:
=AVERAGE(D2:D1001)Para calcular el beneficio mínimo esperado cada mes, escribe lo siguiente en una celda, por ejemplo, G7:
=MIN(D2:D1001)Para calcular el beneficio máximo esperado cada mes, escribe lo siguiente en una celda, por ejemplo, G8:
=MAX(D2:D1001)Para hallar la desviación estándar de los beneficios, escribe lo siguiente en una celda, por ejemplo, G9:
=STDEV.P(D2:D1001)Una vez ejecutada, la hoja de Excel debería tener un aspecto similar al siguiente:
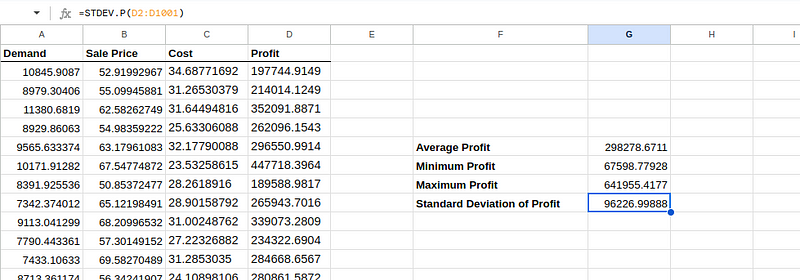
Análisis de los resultados de la simulación.
Podemos interpretar los resultados estimados y las implicaciones para el lanzamiento del producto de la siguiente manera:
- La cifra de beneficio medio representa el beneficio esperado por el lanzamiento del nuevo monitor de actividad física. Esto sugiere que, en promedio, cada simulación predice que podríamos esperar obtener unos beneficios de alrededor de 298 278,67 dólares. Este valor es útil como estimación central de la rentabilidad bajo los supuestos dados.
- Un beneficio mínimo de 67 598,78 dólares es el beneficio más bajo observado en todas nuestras simulaciones. Indica el peor escenario posible según las hipótesis de tu modelo, que sigue siendo rentable, pero significativamente menos que la media. Esto podría deberse a una demanda especialmente baja o a condiciones de costes desfavorables en esa simulación específica.
- Un beneficio máximo de 641 955,42 dólares representa el mejor escenario posible, en el que la demanda y el precio probablemente alcanzaron su nivel más alto y los costes su nivel más bajo en todas las simulaciones. Esto muestra el potencial alcista si las condiciones resultan ser muy favorables.
Dada la amplia diferencia entre los beneficios mínimos y máximos y la considerable desviación estándar, el lanzamiento del nuevo producto conlleva un riesgo financiero considerable.
Los responsables de la toma de decisiones deben considerar si la empresa se siente cómoda con este nivel de incertidumbre y la posibilidad de obtener beneficios inferiores a la media.
Además, aunque es opcional, te recomendamos que crees visualizaciones, como histogramas, para comprender de forma visual los resultados de las simulaciones.
Técnicas para mejorar las simulaciones de Monte Carlo en Excel
Al volver a ejecutar la misma simulación anterior, se puede observar una ligera diferencia en los cálculos, como se muestra a continuación:
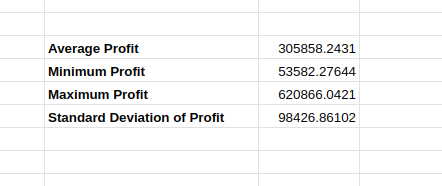
Resultados variables de la simulación.
Esto se debe a que los valores de la simulación original pueden cambiar entre iteraciones, lo que influye en las estimaciones resultantes. Aunque la variación es pequeña, cuando cambia el valor estimado, surge en la mente de los responsables de la toma de decisiones una preocupación por la precisión y fiabilidad de la simulación.
Exploremos algunas técnicas avanzadas que podríamos utilizar para mejorar la precisión y la fiabilidad de las simulaciones.
Aumentar el número de simulaciones
Realizar un mayor número de simulaciones ayuda a promediar las fluctuaciones aleatorias y proporciona una estimación más estable y precisa de los resultados.
Para el ejemplo anterior, podemos aumentar el número de ejecuciones de simulación (por ejemplo, de 1000 a 10 000 o más), especialmente cuando se trata de parámetros muy variables.
Determinar el número «adecuado» de simulaciones depende de varios factores.
Cuanto más complejo es el modelo (es decir, cuantas más variables y mayor sea el rango de sus interacciones), más simulaciones se necesitan normalmente para capturar todos los resultados posibles y garantizar que los resultados no se deban al azar.
Si las entradas tienen una alta variabilidad o están muy sesgadas, serán necesarias más simulaciones para estimar con precisión los extremos (valores extremos) de las distribuciones de resultados.
Para análisis más detallados, especialmente en finanzas o gestión de riesgos, no es raro realizar entre 10 000 y 100 000 simulaciones. Este rango se utiliza normalmente para garantizar resultados sólidos en diversos escenarios y entradas. Por supuesto, como mencionamos anteriormente, para un análisis a tan gran escala, Excel no siempre es la mejor herramienta, sino más bien R o Python.
Refinamiento de las distribuciones de entrada
La precisión de las simulaciones depende en gran medida de la capacidad de las distribuciones de probabilidad de entrada para reflejar la incertidumbre y el comportamiento reales de las variables subyacentes. En nuestro ejemplo anterior, hemos supuesto una distribución normal para la demanda y el coste, y una distribución uniforme para el precio de venta.
Además, podríamos analizar datos históricos más completos para parametrizar mejor las distribuciones. Podemos comprender mejor los comportamientos de los costes, las ventas y la demanda en función de factores externos basándonos en la información proporcionada por expertos en la materia. También podemos considerar el uso de distribuciones como log-normal, beta o gamma, o crear distribuciones personalizadas basadas en datos empíricos.
Realización de un análisis de sensibilidad
Este análisis se realiza para comprender qué variables de entrada tienen el impacto más significativo en el resultado, variando sistemáticamente cada entrada mientras se mantienen constantes las demás.
En nuestro ejemplo anterior, podemos mantener constantes dos variables y cambiar la distribución de una de ellas para comprender los cambios en las estimaciones. A continuación, repite el mismo proceso con las dos variables restantes, una por una. En última instancia, esta técnica ayuda a comprender en qué variable hay que centrar los esfuerzos para mejorar la precisión.
El uso iterativo de las técnicas anteriores y el análisis de los resultados pueden conducir a resultados más precisos y fiables.
Conclusión
Este tutorial te ha presentado la simulación de Monte Carlo y los conceptos estadísticos relevantes. Tras presentar las funciones relevantes de Excel, el tutorial proporcionó una guía paso a paso para implementar la simulación de Monte Carlo en Excel utilizando un ejemplo real.
Por último, has aprendido algunas prácticas recomendadas y técnicas avanzadas para garantizar que tus resultados sean más precisos y fiables.
Si te interesa especialmente implementar la simulación de Monte Carlo anterior utilizando otras herramientas como Python o R, estos dos recursos te resultarán útiles:
Por otra parte, si prefieres seguir utilizando el conocido Microsoft Excel y deseas dominar tus habilidades con esta herramienta tan extendida, te recomendamos que eches un vistazo a nuestro programa Fundamentos de Excel.
Avanza en tu carrera con Excel
Adquiere los conocimientos necesarios para sacar el máximo partido a Excel, sin necesidad de experiencia.

Como científico de datos senior, diseño, desarrollo e implanto soluciones de aprendizaje automático a gran escala para ayudar a las empresas a tomar mejores decisiones basadas en datos. Como escritora de ciencia de datos, comparto aprendizajes, consejos profesionales y tutoriales prácticos en profundidad.