Curso
Os métodos Monte Carlo, que tiraram o nome do Casino de Monte Carlo, em Mônaco, são muito usados em áreas como finanças, engenharia, cadeia de suprimentos e ciência para modelar fenômenos com muita incerteza nas entradas.
Mas o que é simulação de Monte Carlo? Como isso funciona? E como posso implementar a simulação e analisar os resultados?
Este tutorial vai te apresentar a simulação de Monte Carlo e os conceitos estatísticos relevantes por trás da técnica. Também vamos implementar a simulação de Monte Carlo no Excel, familiarizando você com as funções integradas relevantes do Excel.
Por fim, o tutorial vai te mostrar as melhores práticas, técnicas avançadas e recursos adicionais, tornando-o o seu guia completo para aprender tudo sobre simulação de Monte Carlo no Microsoft Excel.
O que é simulação de Monte Carlo?
A simulação de Monte Carlo é uma técnica matemática usada para modelar a probabilidade de diferentes resultados em um processo que não pode ser facilmente previsto devido à intervenção de variáveis aleatórias.
É uma ferramenta poderosa para entender o impacto do risco e da incerteza em vários campos. O método se baseia em amostragens aleatórias repetidas para simular o comportamento de sistemas e processos complexos.
O problema é primeiro modelado por uma distribuição de probabilidade para cada variável que tem incerteza inerente. Um monte de amostras aleatórias são tiradas dessas distribuições de probabilidade, e essas amostras são usadas para calcular os resultados. Esse processo é repetido várias vezes para criar uma distribuição de resultados possíveis, que podem ser analisados estatisticamente para fornecer previsões sobre como um sistema se comportará.
Então, em termos simples. A simulação de Monte Carlo é uma técnica que prevê como sistemas complexos vão se comportar, simulando seus resultados várias vezes usando valores aleatórios. Ele usa várias etapas:
- Incerteza do modelo: Defina como cada variável pode variar usando distribuições de probabilidade.
- Amostragem aleatória: Escolha valores aleatoriamente para essas variáveis com base nas suas distribuições.
- Simule resultados: Use esses valores para simular o comportamento do sistema.
- Analise os resultados: Repita o processo várias vezes para obter uma série de resultados possíveis e, em seguida, analise-os para prever os cenários mais prováveis.
A seguir, vamos construir nossa compreensão básica da simulação de Monte Carlo, aprofundando-nos em alguns conceitos estatísticos relevantes.
Variáveis aleatórias e distribuições de Monte Carlo
Variáveis aleatórias e suas distribuições de probabilidade associadas são fundamentais para a simulação de Monte Carlo, pois fornecem a estrutura matemática para modelar e simular a aleatoriedade e a variabilidade inerentes a sistemas complexos.
Variáveis aleatórias
Uma variável aleatória é uma variável cujos valores são resultados de um fenômeno aleatório.
As variáveis aleatórias são classificadas em dois tipos:
- Variáveis aleatórias discretas: Essas variáveis assumem um número contável de valores distintos. Nas simulações, variáveis discretas podem modelar cenários como o número de itens com defeito em um lote, chegadas de clientes por hora ou outros eventos contáveis.
- Variáveis aleatórias contínuas: Essas variáveis podem assumir qualquer valor em um intervalo contínuo. Variáveis contínuas são usadas para simulações que lidam com medições físicas ou durações de tempo.
As variáveis aleatórias são usadas em simulações porque elas têm aquela incerteza que as técnicas de Monte Carlo foram feitas pra explorar e quantificar.
Distribuições de probabilidade
As distribuições de probabilidade mostram como as probabilidades se espalham pelos valores de uma variável aleatória.
As distribuições de probabilidade são usadas na simulação de Monte Carlo para definir como diferentes entradas ou cenários devem se comportar, o que é essencial para uma modelagem precisa e tomada de decisões.
A distribuição normal é a mais usada em estatística e simulações porque muitos fenômenos naturais e artificiais tendem a seguir essa distribuição por causa do Teorema do Limite Central.
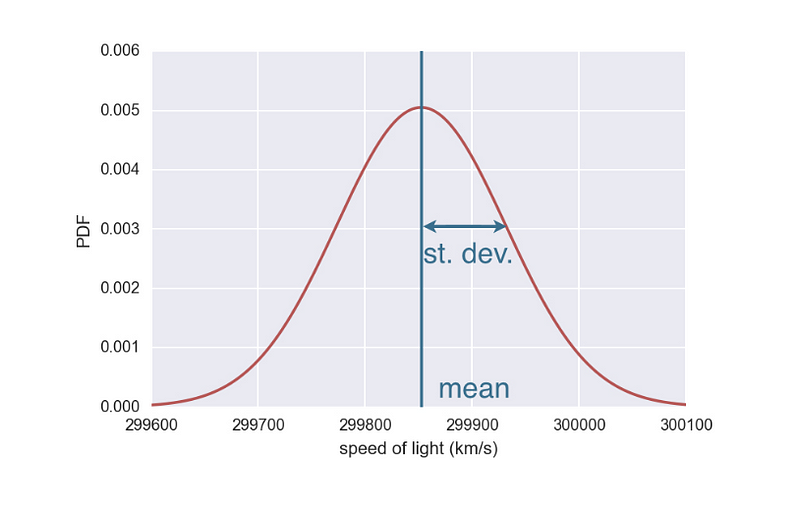
Distribuição normal (Fonte)
A distribuição normal é usada para modelar variáveis que são influenciadas por muitos efeitos pequenos e independentes, como erros de medição ou retornos do mercado de ações.
Outras distribuições de probabilidade são as distribuições uniformes, que são usadas quando qualquer resultado em um intervalo específico tem a mesma chance de acontecer — uma suposição comum em simulações quando não há dados anteriores disponíveis — e as distribuições binomiais, que são usadas na modelagem de cenários com dois resultados possíveis (sucesso/fracasso) em uma série de experimentos, como testes de aprovação/reprovação ou verificações de controle de qualidade.
Agora que entendemos os conceitos e a teoria por trás das simulações de Monte Carlo, vamos passar para a parte da implementação.
Aprenda os fundamentos do Excel
Por que usar o Excel para simulação de Monte Carlo?
Depois de decidir fazer uma simulação de Monte Carlo, você tem várias ferramentas, como Excel, Python, R, SAS e MATLAB, pra te ajudar com as simulações.
O fator mais importante a considerar, especialmente ao implementar a simulação de Monte Carlo pela primeira vez, é a sua familiaridade geral com a ferramenta. O Excel é uma das ferramentas mais usadas no mundo dos negócios, o que significa que muita gente já conhece suas funções básicas. Isso reduz o tempo de treinamento e elimina a necessidade de aprender um novo software do zero.
O Excel também oferece ferramentas fáceis de usar para criar tabelas e gráficos, que podem ser úteis para visualizar os resultados das simulações. Além disso, vários complementos poderosos estão disponíveis para o Excel, aumentando sua capacidade de realizar simulações complexas de Monte Carlo.
Mas, vale lembrar que, pra simulações mais avançadas, principalmente aquelas que precisam lidar com muitos dados ou fazer um monte de simulações, pode ser melhor usar outras ferramentas mais especializadas, além do Excel.
Principais funções do Excel para Monte Carlo
A seguir, vamos ver duas funções essenciais do Excel: RAND() e NORM.INV(), falando sobre sua sintaxe, parâmetros e casos típicos de uso. Essas funções ajudam a gerar números aleatórios e definir distribuições de probabilidade, que são aspectos fundamentais de qualquer simulação.
A função RAND()
RAND() gera um número aleatório maior ou igual a 0 e menor que 1. Os números estão distribuídos uniformemente, o que significa que qualquer número dentro do intervalo especificado tem a mesma probabilidade de aparecer.
A sintaxe para RAND() é a seguinte:
RAND()A função ` RAND() ` não precisa de nenhum argumento. É usado simplesmente como RAND().
No contexto da Simulação de Monte Carlo, o RAND() pode ser usado para simular a ocorrência de eventos aleatórios ou para variar as entradas no seu modelo.
A função NORM.INV()
Enquanto RAND() gera números aleatórios uniformes, NORM.INV() é usado para gerar números aleatórios a partir de uma distribuição normal, o que é um requisito comum em uma simulação de Monte Carlo. Essa função mostra o inverso da distribuição cumulativa normal para uma média e um desvio padrão específicos.
A sintaxe da função ` NORM.INV() ` é a seguinte:
NORM.INV(probability, mean, standard_deviation)Os parâmetros são:
-
probability: Uma probabilidade que corresponde à distribuição normal, que precisa ser um valor entre 0 e 1. Isso geralmente é gerado pela funçãoRAND(). -
mean: A média aritmética da distribuição normal. -
standard_deviation: O desvio padrão da distribuição normal, uma medida de como os números estão espalhados em torno da média.
A função “ NORM.INV() ” é usada para transformar números aleatórios distribuídos uniformemente da função “ RAND() ” em números que seguem uma distribuição normal específica. Isso é útil pra modelar variáveis que devem apresentar variabilidade natural seguindo uma curva normal.
Agora que já temos todos os blocos de construção, funções e conceitos por trás de uma simulação de Monte Carlo, vamos implementar uma no Microsoft Excel.
Implementando a simulação de Monte Carlo no Microsoft Excel: Um exemplo
Imagina que você é um analista de dados trabalhando numa empresa de eletrônicos de consumo super dinâmica e foi encarregado de avaliar se vale a pena lançar um novo monitor de fitness vestível.
O mercado para esses aparelhos é bem competitivo e a procura dos consumidores pode variar bastante, dependendo das tendências sazonais, da eficácia do marketing e das ações dos concorrentes. Além disso, os custos de fabricar esses aparelhos podem mudar por causa das variações nos preços dos materiais e das incertezas na cadeia de suprimentos.
Você decidiu usar a simulação de Monte Carlo no Excel para resolver esses desafios. Você acha que essa abordagem vai te ajudar a estimar a lucratividade potencial em diferentes cenários, permitindo que a empresa tome decisões bem informadas sobre estratégias de preços, volumes de produção e investimentos em marketing.
Você também analisou dados anteriores de lançamentos de produtos parecidos e estudos de mercado dentro da indústria de eletrônicos de consumo. A partir dessa análise, você chegou a algumas conclusões que vão ajudar na sua simulação:
- Uma demanda média de 10.000 unidades para novos dispositivos no primeiro ano de lançamento, com um desvio padrão de 2.000 unidades, refletindo a incerteza na aceitação do consumidor.
- O preço de venda por unidade geralmente fica entre US$ 50 e US$ 70, dependendo dos preços da concorrência e da saturação do mercado.
- O custo unitário, que é afetado pelos preços instáveis dos materiais e pela eficiência da fabricação, é em média de US$ 30 por unidade, com um desvio padrão de US$ 5.
Esses dados históricos são a base dos seus parâmetros de simulação, ajudando a criar uma simulação que reflete as condições atuais do mercado com mais precisão.
Os passos que você pode seguir para implementar a simulação de Monte Carlo para este exemplo específico são os seguintes:
Passo 1: Configure sua planilha do Excel
Primeiro, prepare sua planilha do Excel para incluir colunas para cada variável e uma coluna para o lucro calculado.
Aqui está como ficaria inicialmente:
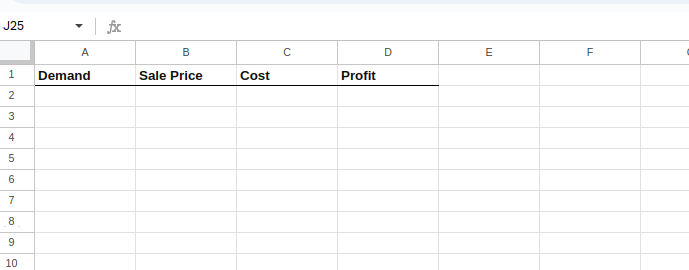
Configurando a planilha do Excel.
Passo 2: Formulários de entrada para variáveis
Em cada linha, você vai colocar fórmulas pra gerar valores aleatórios pra demanda, preço de venda e custo com base nas distribuições que você identificou:
- Demanda: Distribuição normal (média = 10.000 unidades, desvio padrão = 2.000 unidades)
- Preço de venda: Distribuição uniforme (50 a 70 dólares)
- Custo: Distribuição normal (média = $30, desvio padrão = $5)
Para inserir essas fórmulas uma a uma, selecione a célula A2 e digite o seguinte:
=NORM.INV(RAND(), 10000, 2000)A equação acima cria uma distribuição normal com uma média e um desvio padrão determinados, conforme mostrado abaixo:
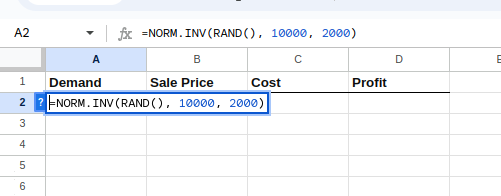
Criando a distribuição para a demanda.
Depois, selecione a célula B2 e digite o seguinte:
=50 + (70-50) * RAND()A equação acima cria uma distribuição uniforme entre $50 e $70 para o preço de venda, conforme abaixo:
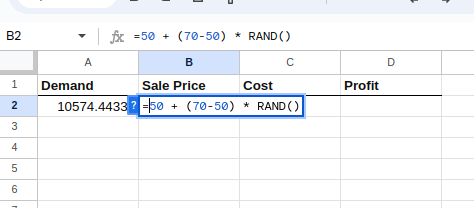
Criando a distribuição para o preço de venda.
Selecione a célula C2 e digite o seguinte:
=NORM.INV(RAND(), 30, 5)A equação acima, parecida com a equação da demanda, cria uma distribuição normal com uma média e um desvio padrão específicos, como mostrado abaixo:
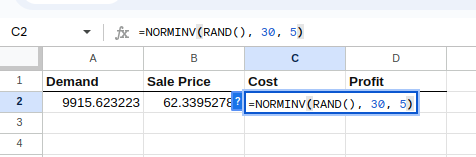
Criando a distribuição para custos.
Passo 3: Calcule a variável dependente
Agora, calcule o lucro, que é a variável dependente, para cada simulação usando a fórmula na coluna D:
=(B2 - C2) * A2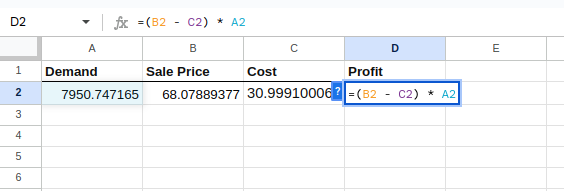
Calculando o lucro.
Passo 4: Preencha para simular vários cenários
O que fizemos até agora foi criar uma única simulação. Vamos estender isso para várias, digamos, mil simulações.
Selecione as células A2 a D2 e arraste a alça de preenchimento (um pequeno quadrado no canto inferior direito da seleção) para baixo para preencher as fórmulas em quantas linhas você quiser simular (por exemplo, 1000 linhas para 1000 simulações).
Vai ficar mais ou menos assim:
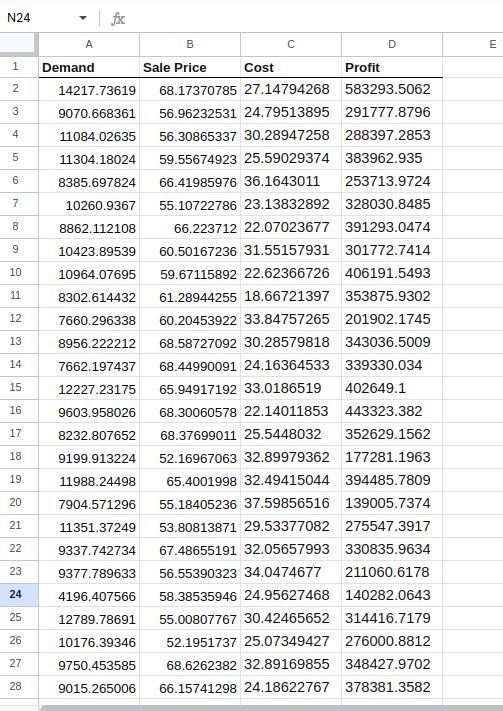
Fazendo as simulações.
Passo 5: Analise os resultados
Depois de fazer as simulações, dá pra analisar os resultados usando funções estatísticas como mínimo, máximo, média e desvios padrão. Não hesite em consultar rapidamente a folha de dicas do Excel para relembrar as funções integradas do Excel que usaremos a seguir.
Para descobrir o lucro médio esperado por mês, digite o seguinte em uma célula, tipo G6:
=AVERAGE(D2:D1001)Para descobrir o lucro mínimo esperado por mês, digite o seguinte em uma célula, tipo G7:
=MIN(D2:D1001)Para descobrir o lucro máximo esperado por mês, digite o seguinte em uma célula, tipo G8:
=MAX(D2:D1001)Para descobrir o desvio padrão do lucro, digite o seguinte em uma célula, tipo G9:
=STDEV.P(D2:D1001)Depois de executada, a planilha do Excel deve ficar mais ou menos assim:
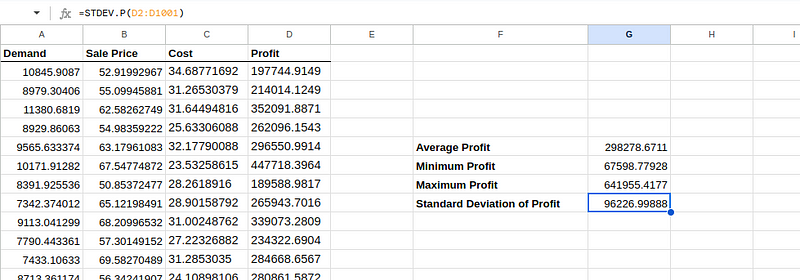
Analisando os resultados da simulação.
A gente pode ver os resultados estimados e o que isso quer dizer para o lançamento do produto assim:
- O valor médio do lucro representa o lucro esperado com o lançamento do novo monitor de fitness. Isso sugere que, em média, cada simulação prevê que poderíamos esperar um lucro de cerca de US$ 298.278,67. Esse valor é útil como uma estimativa central da rentabilidade sob as premissas dadas.
- Um lucro mínimo de $67.598,78 é o menor lucro observado em todas as nossas simulações. Isso mostra o pior cenário possível com base nas suposições do seu modelo, que ainda dá lucro, mas bem menos do que a média. Isso pode ser por causa de uma demanda bem baixa ou de condições de custo nada legais nessa simulação específica.
- Um lucro máximo de $641.955,42 é o melhor cenário possível, onde a demanda e o preço provavelmente estavam no máximo e os custos no mínimo em todas as simulações. Isso mostra o potencial de crescimento se as condições forem super favoráveis.
Dada a grande variação entre os lucros mínimos e máximos e o desvio padrão substancial, há um risco financeiro considerável associado ao lançamento do novo produto.
Os tomadores de decisão devem pensar se a empresa está tranquila com esse nível de incerteza e a possibilidade de lucros abaixo da média.
Além disso, embora seja opcional, a gente recomenda que você crie visualizações, como histogramas, para ter uma compreensão visual dos resultados das simulações.
Técnicas para melhorar as simulações de Monte Carlo no Excel
Quando você refaz a mesma simulação de antes, dá pra ver uma pequena diferença nos cálculos, como mostra a imagem abaixo:
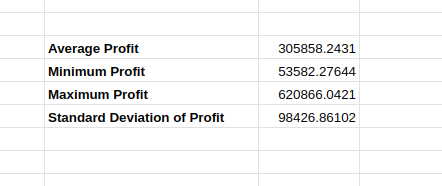
Resultados variáveis da simulação.
Isso porque os valores da simulação original podem mudar entre as iterações, afetando as estimativas finais. Mesmo que a variação seja pequena, quando o valor estimado muda, surge uma preocupação sobre a precisão e a confiabilidade da simulação na cabeça dos tomadores de decisão.
Vamos ver algumas técnicas avançadas que a gente pode usar pra melhorar a precisão e a confiabilidade das simulações.
Aumentando o número de simulações
Fazer várias simulações ajuda a equilibrar as variações aleatórias e dá uma estimativa mais estável e precisa dos resultados.
Para o exemplo acima, podemos aumentar o número de execuções da simulação (por exemplo, de 1.000 para 10.000 ou mais), especialmente quando lidamos com parâmetros altamente variáveis.
Determinar o número “certo” de simulações depende de vários fatores.
Quanto mais complicado for o modelo (ou seja, quanto mais variáveis e mais interações entre elas), mais simulações geralmente são necessárias para pegar todos os resultados possíveis e garantir que os resultados não sejam por acaso.
Se os dados de entrada tiverem muita variabilidade ou estiverem bem distorcidos, vai ser preciso fazer mais simulações para estimar com precisão as extremidades (valores extremos) das distribuições dos resultados.
Para análises mais detalhadas, principalmente em finanças ou gestão de riscos, não é raro fazer de 10.000 a 100.000 simulações. Esse intervalo é normalmente usado para garantir resultados robustos em vários cenários e entradas. Claro, como falamos antes, pra uma análise tão grande, o Excel nem sempre é a melhor opção, melhor usar R ou Python.
Aperfeiçoando as distribuições de entrada
A precisão das simulações depende muito de como as distribuições de probabilidade de entrada refletem a incerteza e o comportamento reais das variáveis subjacentes. No nosso exemplo acima, assumimos uma distribuição normal para a demanda e o custo e uma distribuição uniforme para o preço de venda.
Além disso, poderíamos analisar dados históricos mais abrangentes para parametrizar melhor as distribuições. Podemos entender melhor como o custo, a venda e a demanda se comportam em relação a fatores externos com base nas opiniões de especialistas na área. Também podemos pensar em usar distribuições como log-normal, beta ou gama, ou criar distribuições personalizadas com base em dados empíricos.
Fazendo uma análise de sensibilidade
Essa análise é feita para entender quais variáveis de entrada têm o impacto mais significativo na saída, variando sistematicamente cada entrada enquanto mantém as outras constantes.
No nosso exemplo acima, podemos manter duas variáveis constantes e alterar a distribuição de uma delas para entender as mudanças nas estimativas. Depois, repete o mesmo processo para as duas variáveis restantes, uma por uma. No fim das contas, essa técnica ajuda a entender em qual variável concentrar os esforços para melhorar a precisão.
Usar essas técnicas várias vezes e ver os resultados pode ajudar a ter resultados mais precisos e confiáveis.
Conclusão
Este tutorial apresentou a Simulação de Monte Carlo e os conceitos estatísticos relevantes. Depois de apresentar as funções relevantes do Excel, o tutorial deu um passo a passo pra implementar a Simulação de Monte Carlo no Excel usando um exemplo da vida real.
Por fim, você aprendeu algumas práticas recomendadas e técnicas avançadas para garantir que seus resultados sejam mais precisos e confiáveis.
Se você estiver interessado em implementar a simulação de Monte Carlo acima usando outras ferramentas, como Python ou R, esses dois recursos podem ser úteis:
Se você preferir continuar com o familiar Microsoft Excel e quiser dominar suas habilidades usando essa ferramenta amplamente adotada, dê uma olhada em nosso programa Fundamentos do Excel.
Avance em sua carreira com o Excel
Adquira as habilidades para maximizar o Excel - não é necessário ter experiência.

Como cientista de dados sênior, eu projeto, desenvolvo e implanto soluções de aprendizado de máquina em larga escala para ajudar as empresas a tomar melhores decisões baseadas em dados. Como redator de ciência de dados, compartilho aprendizados, conselhos de carreira e tutoriais práticos e detalhados.


