Kurs
Monte-Carlo-Methoden, die ihren Namen vom Monte-Carlo-Casino in Monaco haben, werden oft in Bereichen wie Finanzen, Technik, Lieferketten und Wissenschaft benutzt, um Phänomene mit großer Unsicherheit in den Eingaben zu modellieren.
Aber was ist eigentlich eine Monte-Carlo-Simulation? Wie läuft das ab? Und wie kann ich die Simulation machen und die Ergebnisse anschauen?
In diesem Tutorial lernst du die Monte-Carlo-Simulation und die wichtigen statistischen Konzepte kennen, die hinter dieser Technik stehen. Wir werden auch die Monte-Carlo-Simulation in Excel machen und dir dabei die passenden Excel-Funktionen zeigen.
Zum Schluss bekommst du noch ein paar Tipps, fortgeschrittene Techniken und weitere Ressourcen, sodass dieses Tutorial dein Komplettpaket ist, um alles über Monte-Carlo-Simulationen in Microsoft Excel zu lernen.
Was ist eine Monte-Carlo-Simulation?
Die Monte-Carlo-Simulation ist eine mathematische Technik, mit der man die Wahrscheinlichkeit verschiedener Ergebnisse in einem Prozess modelliert, der wegen Zufallsgrößen schwer vorherzusagen ist.
Es ist ein echt starkes Tool, um die Auswirkungen von Risiken und Unsicherheiten in verschiedenen Bereichen zu verstehen. Die Methode nutzt wiederholte Zufallsstichproben, um das Verhalten von komplexen Systemen und Prozessen zu simulieren.
Das Problem wird zuerst durch eine Wahrscheinlichkeitsverteilung für jede Variable modelliert, die eine inhärente Unsicherheit hat. Dann werden viele Zufallsstichproben aus diesen Wahrscheinlichkeitsverteilungen gezogen, und mit diesen Stichproben werden die Ergebnisse berechnet. Dieser Vorgang wird oft wiederholt, um eine Verteilung möglicher Ergebnisse zu erstellen, die statistisch analysiert werden kann, um Vorhersagen über das Verhalten eines Systems zu treffen.
Also, einfach gesagt. Die Monte-Carlo-Simulation ist eine Technik, die vorhersagt, wie sich komplexe Systeme verhalten werden, indem sie ihre Ergebnisse viele Male mit Zufallswerten simuliert. Es geht in mehreren Schritten:
- Modellunsicherheit: Definiere, wie sich jede Variable anhand von Wahrscheinlichkeitsverteilungen ändern kann.
- Zufallsstichprobe: Wähle Werte für diese Variablen nach dem Zufallsprinzip aus, basierend auf ihren Verteilungen.
- Ergebnisse simulieren: Benutz diese Werte, um das Verhalten des Systems zu simulieren.
- Analysiere die Ergebnisse: Mach das Ganze ein paar Mal, um verschiedene mögliche Ergebnisse zu kriegen, und schau dir die dann an, um die wahrscheinlichsten Szenarien vorherzusagen.
Als Nächstes werden wir unser grundlegendes Verständnis der Monte-Carlo-Simulation vertiefen, indem wir uns mit einigen relevanten statistischen Konzepten beschäftigen.
Monte-Carlo-Zufallsvariablen und -Verteilungen
Zufallsvariablen und die dazugehörigen Wahrscheinlichkeitsverteilungen sind echt wichtig für die Monte-Carlo-Simulation, weil sie den mathematischen Rahmen für die Modellierung und Simulation der Zufälligkeit und Variabilität bieten, die in komplexen Systemen vorkommen.
Zufallsgrößen
Eine Zufallsvariable ist eine Variable, deren Werte das Ergebnis eines zufälligen Ereignisses sind.
Zufallsgrößen gibt's in zwei Arten:
- Diskrete Zufallsvariablen: Diese Variablen können eine endliche Anzahl unterschiedlicher Werte annehmen. In Simulationen können diskrete Variablen Szenarien wie die Anzahl fehlerhafter Artikel in einer Charge, die Anzahl der Kunden pro Stunde oder andere zählbare Ereignisse modellieren.
- Kontinuierliche Zufallsvariablen: Diese Variablen können beliebige Werte in einem kontinuierlichen Bereich annehmen. Kontinuierliche Variablen werden für Simulationen verwendet, die sich mit physikalischen Messungen oder Zeitdauern beschäftigen.
Zufallsvariablen werden in Simulationen verwendet, weil sie die Unsicherheit beinhalten, die mit Monte-Carlo-Techniken untersucht und quantifiziert werden soll.
Wahrscheinlichkeitsverteilungen
Wahrscheinlichkeitsverteilungen zeigen, wie die Wahrscheinlichkeiten über die Werte einer Zufallsvariablen verteilt sind.
Wahrscheinlichkeitsverteilungen werden in der Monte-Carlo-Simulation verwendet, um zu definieren, wie sich verschiedene Eingaben oder Szenarien voraussichtlich verhalten werden, was für eine genaue Modellierung und Entscheidungsfindung unerlässlich ist.
Die Normalverteilung ist die am häufigsten verwendete Verteilung in der Statistik und in Simulationen, weil viele natürliche und vom Menschen verursachte Phänomene aufgrund des zentralen Grenzwertsatzes dazu neigen, dieser Verteilung zu folgen .
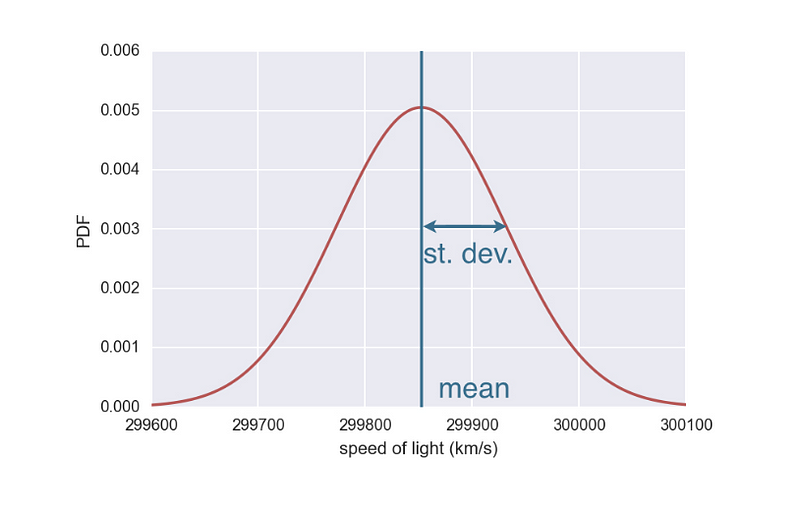
Normalverteilung (Quelle)
Die Normalverteilung wird benutzt, um Variablen zu modellieren, die von vielen kleinen, unabhängigen Effekten beeinflusst werden, wie zum Beispiel Messfehler oder Börsenrenditen.
Andere Wahrscheinlichkeitsverteilungen sind Gleichverteilungen, die man benutzt, wenn jedes Ergebnis in einem bestimmten Bereich gleich wahrscheinlich ist – eine häufige Annahme in Simulationen, wenn keine früheren Daten da sind. Dann gibt's noch Binomialverteilungen, die man bei der Modellierung von Szenarien mit zwei möglichen Ergebnissen (Erfolg/Misserfolg) in einer Reihe von Experimenten benutzt, wie zum Beispiel bei Pass/Fail-Tests oder Qualitätskontrollen.
Nachdem wir jetzt die Konzepte und die Theorie hinter Monte-Carlo-Simulationen verstanden haben, schauen wir uns mal die praktische Umsetzung an.
Excel-Grundlagen lernen
Warum Excel für Monte-Carlo-Simulationen nutzen?
Wenn du dich für eine Monte-Carlo-Simulation entschieden hast, stehen dir verschiedene Tools wie Excel, Python, R, SAS und MATLAB zur Verfügung, die dir bei den Simulationen helfen.
Der wichtigste Punkt, den du beachten solltest, vor allem wenn du die Monte-Carlo-Simulation zum ersten Mal machst, ist, wie gut du mit dem Tool klarkommst. Excel ist eines der am häufigsten verwendeten Tools in der Geschäftswelt, was bedeutet, dass viele Leute bereits mit seinen Grundfunktionen vertraut sind. Das verkürzt die Einarbeitungszeit und man muss keine neue Software von Grund auf lernen.
Excel hat auch coole Tools zum Erstellen von Diagrammen und Grafiken, die echt praktisch sein können, um die Ergebnisse von Simulationen zu zeigen. Außerdem gibt's für Excel ein paar coole Add-Ins, die die Möglichkeiten für komplexe Monte-Carlo-Simulationen erweitern.
Man sollte aber auch bedenken, dass für anspruchsvollere Simulationen, vor allem wenn man mit großen Datenmengen arbeitet oder viele Simulationen machen muss, andere Tools als Excel vielleicht besser passen.
Wichtige Excel-Funktionen für Monte Carlo
Als Nächstes schauen wir uns zwei wichtige Excel-Funktionen an: „ RAND() “ und „ NORM.INV() “. Dabei gehen wir auf ihre Syntax, Parameter und typischen Anwendungsfälle ein. Diese Funktionen helfen dabei, Zufallszahlen zu erzeugen und Wahrscheinlichkeitsverteilungen zu definieren, die grundlegende Aspekte jeder Simulation sind.
Die Funktion RAND()
RAND() macht eine Zufallszahl, die größer oder gleich 0 und kleiner als 1 ist. Die Zahlen sind gleichmäßig verteilt, was bedeutet, dass jede Zahl innerhalb des angegebenen Bereichs mit gleicher Wahrscheinlichkeit vorkommen kann.
Die Syntax für „ RAND() “ sieht so aus:
RAND()Die Funktion „ RAND() “ braucht keine Argumente. Es wird einfach als RAND() benutzt.
Bei der Monte-Carlo-Simulation kann man „ RAND() “ nutzen, um zufällige Ereignisse zu simulieren oder die Eingaben in dein Modell zu variieren.
Die Funktion NORM.INV()
Während „ RAND() “ gleichmäßige Zufallszahlen erzeugt, wird „NORM.INV()“ benutzt, um Zufallszahlen aus einer Normalverteilung zu erzeugen, was bei einer Monte-Carlo-Simulation oft gebraucht wird. Diese Funktion gibt den Kehrwert der normalen Verteilungsfunktion für einen bestimmten Mittelwert und eine bestimmte Standardabweichung zurück.
Die Syntax für die Funktion „ NORM.INV() “ sieht so aus:
NORM.INV(probability, mean, standard_deviation)Die Parameter sind:
-
probability: Eine Wahrscheinlichkeit, die der Normalverteilung entspricht und zwischen 0 und 1 liegen muss. Das wird normalerweise von der Funktion „RAND()“ gemacht. -
mean: Der arithmetische Mittelwert der Normalverteilung. -
standard_deviation: Die Standardabweichung der Normalverteilung, die zeigt, wie weit die Zahlen um den Mittelwert verteilt sind.
Die Funktion „ NORM.INV() ” wandelt gleichmäßig verteilte Zufallszahlen aus der Funktion „ RAND() ” in Zahlen um, die einer bestimmten Normalverteilung folgen. Das ist praktisch, wenn man Variablen modellieren will, die sich wahrscheinlich wie eine normale Kurve verhalten.
Jetzt, wo wir alle Bausteine, Funktionen und Konzepte einer Monte-Carlo-Simulation kennen, lass uns eine in Microsoft Excel umsetzen.
Implementierung der Monte-Carlo-Simulation in Microsoft Excel: Ein Beispiel
Stell dir vor, du bist Datenanalyst bei einem coolen Unternehmen für Unterhaltungselektronik und sollst die finanzielle Machbarkeit der Einführung eines neuen tragbaren Fitness-Trackers checken.
Der Markt für solche Geräte ist hart umkämpft, und die Nachfrage der Verbraucher kann stark schwanken, weil sie von saisonalen Trends, der Wirksamkeit des Marketings und den Maßnahmen der Konkurrenz beeinflusst wird. Außerdem können die Kosten für die Herstellung dieser Geräte wegen Materialpreisänderungen und Unsicherheiten in der Lieferkette schwanken.
Du hast dich entschieden, die Monte-Carlo-Simulation in Excel zu nutzen, um diese Herausforderungen anzugehen. Du denkst, dass dieser Ansatz dir dabei hilft, die potenzielle Rentabilität unter verschiedenen Szenarien abzuschätzen, sodass das Unternehmen fundierte Entscheidungen über Preisstrategien, Produktionsmengen und Marketinginvestitionen treffen kann.
Du hast auch alte Daten von ähnlichen Produkteinführungen und Marktstudien in der Unterhaltungselektronikbranche angeschaut. Aus dieser Analyse hast du bestimmte Kennzahlen abgeleitet, die deine Simulation beeinflussen werden:
- Im ersten Jahr nach der Markteinführung wird eine durchschnittliche Nachfrage von 10.000 neuen Geräten erwartet, mit einer Standardabweichung von 2.000 Einheiten, was die Unsicherheit bei der Akzeptanz durch die Verbraucher zeigt.
- Der Verkaufspreis pro Einheit liegt normalerweise zwischen 50 und 70 Dollar, je nachdem, wie die Preise bei der Konkurrenz sind und wie voll der Markt ist.
- Die Stückkosten, die von den schwankenden Materialpreisen und der Produktionseffizienz beeinflusst werden, liegen im Schnitt bei 30 Dollar pro Stück mit einer Standardabweichung von 5 Dollar.
Diese historischen Daten bilden die Grundlage für deine Simulationsparameter und helfen dabei, die Simulation so zu gestalten, dass sie die aktuellen Marktbedingungen genauer widerspiegelt.
Hier sind die Schritte, die du machen kannst, um die Monte-Carlo-Simulation für dieses spezielle Beispiel umzusetzen:
Schritt 1: Richte deine Excel-Tabelle ein
Mach zuerst dein Excel-Arbeitsblatt fertig, mit Spalten für jede Variable und einer Spalte für den berechneten Gewinn.
So würde es am Anfang aussehen:
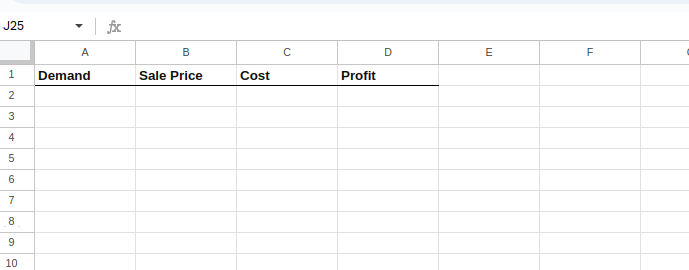
Die Excel-Tabelle einrichten.
Schritt 2: Formeln für Variablen eingeben
In jeder Zeile gibst du Formeln ein, um zufällige Werte für Nachfrage, Verkaufspreis und Kosten basierend auf den von dir ermittelten Verteilungen zu generieren:
- Nachfrage: Normalverteilung (Mittelwert = 10.000 Einheiten, Standardabweichung = 2.000 Einheiten)
- Verkaufspreis: Gleichmäßige Verteilung (50 bis 70 Dollar)
- Kosten: Normalverteilung (Mittelwert = 30 $, Standardabweichung = 5 $)
Um diese Formeln einzeln einzugeben, wähl die Zelle A2 aus und gib Folgendes ein:
=NORM.INV(RAND(), 10000, 2000)Die obige Gleichung ergibt eine Normalverteilung mit einem bestimmten Mittelwert und einer bestimmten Standardabweichung, wie unten gezeigt:
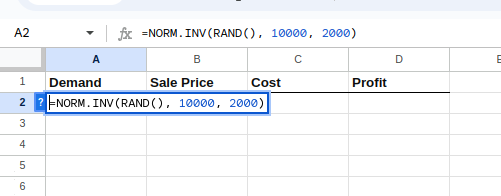
Die Verteilung für die Nachfrage erstellen.
Wähle als Nächstes die Zelle B2 aus und gib Folgendes ein:
=50 + (70-50) * RAND()Die obige Gleichung ergibt eine gleichmäßige Verteilung des Verkaufspreises zwischen 50 und 70 Dollar, wie unten gezeigt:
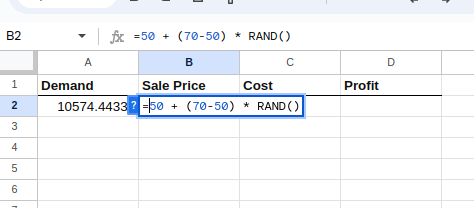
Erstellen der Verteilung für den Verkaufspreis.
Wähle die Zelle C2 aus und gib Folgendes ein:
=NORM.INV(RAND(), 30, 5)Die obige Gleichung erzeugt, ähnlich wie die Nachfragegleichung, eine Normalverteilung mit einem bestimmten Mittelwert und einer bestimmten Standardabweichung, wie unten dargestellt:
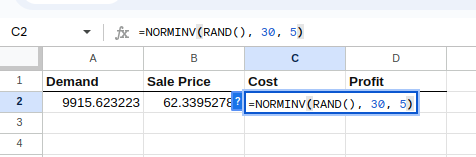
Die Verteilung der Kosten erstellen.
Schritt 3: Berechne die abhängige Variable
Berechne jetzt den Gewinn, also die abhängige Variable, für jede Simulation mit der Formel in Spalte D:
=(B2 - C2) * A2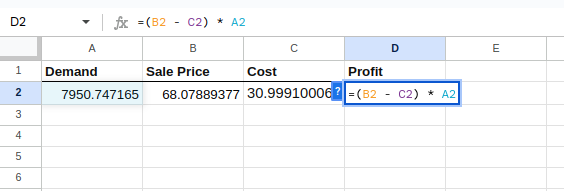
Den Gewinn berechnen.
Schritt 4: Füll das Formular aus, um verschiedene Szenarien zu testen.
Bisher haben wir eine einzige Simulation erstellt. Lass uns das auf mehrere, sagen wir mal tausend Simulationen ausweiten.
Wähle die Zellen A2 bis D2 aus und zieh den Füllgriff (das kleine Quadrat unten rechts in der Auswahl) nach unten, um die Formeln in so viele Zeilen zu kopieren, wie du simulieren willst (z. B. 1000 Zeilen für 1000 Simulationen).
Es wird ungefähr so aussehen:
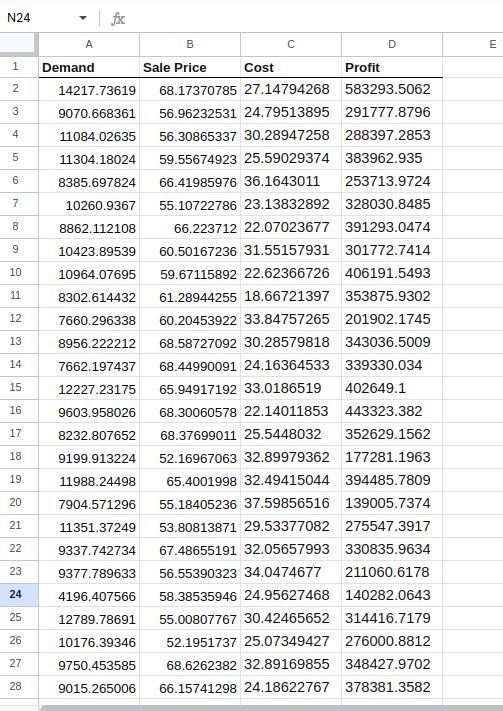
Die Simulationen erstellen.
Schritt 5: Analysiere die Ergebnisse
Nachdem du die Simulationen gemacht hast, kannst du die Ergebnisse mit statistischen Funktionen wie Min, Max, Durchschnitt und Standardabweichungen anschauen. Schau ruhig mal schnell in den Excel-Spickzettel rein, um dich über die integrierten Excel-Funktionen, die wir als Nächstes verwenden werden, auf den neuesten Stand zu bringen.
Um den durchschnittlichen erwarteten Monatsgewinn zu ermitteln, gib Folgendes in eine Zelle ein, zum Beispiel G6:
=AVERAGE(D2:D1001)Um den minimalen erwarteten Monatsgewinn zu ermitteln, gib Folgendes in eine Zelle ein, zum Beispiel G7:
=MIN(D2:D1001)Um den maximalen erwarteten Gewinn pro Monat zu ermitteln, gib Folgendes in eine Zelle ein, zum Beispiel G8:
=MAX(D2:D1001)Um die Standardabweichung des Gewinns zu ermitteln, gib Folgendes in eine Zelle ein, zum Beispiel G9:
=STDEV.P(D2:D1001)Nach der Ausführung sollte die Excel-Tabelle ungefähr so aussehen:
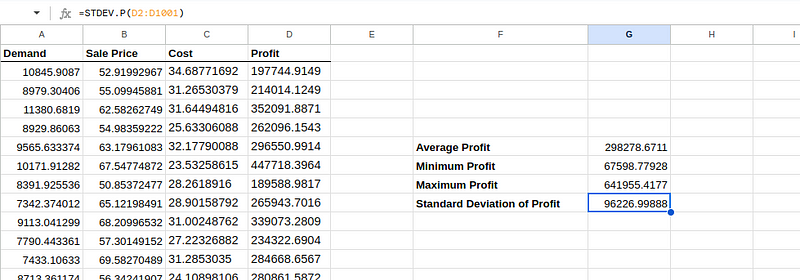
Analyse der Simulationsergebnisse.
Wir können die geschätzten Ergebnisse und die Auswirkungen auf die Produkteinführung wie folgt interpretieren:
- Der durchschnittliche Gewinnwert zeigt den erwarteten Gewinn durch die Einführung des neuen Fitness-Trackers. Das heißt, dass wir bei jeder Simulation im Schnitt mit einem Gewinn von etwa 298.278,67 Dollar rechnen können. Dieser Wert ist nützlich als zentrale Schätzung der Rentabilität unter den gegebenen Annahmen.
- Ein Gewinn von mindestens 67.598,78 $ ist der niedrigste Gewinn, den wir in allen unseren Simulationen gesehen haben. Es zeigt das schlimmste Szenario unter den Annahmen deines Modells, das immer noch profitabel ist, aber deutlich weniger als der Durchschnitt. Das könnte an einer besonders schwachen Nachfrage oder ungünstigen Kostenbedingungen in dieser speziellen Simulation liegen.
- Ein maximaler Gewinn von 641.955,42 $ ist das beste Szenario, bei dem Nachfrage und Preis wahrscheinlich am höchsten und die Kosten in allen Simulationen am niedrigsten waren. Das zeigt, wie viel Potenzial nach oben da ist, wenn die Bedingungen richtig gut sind.
Angesichts der großen Spanne zwischen dem minimalen und maximalen Gewinn und der erheblichen Standardabweichung ist die Einführung des neuen Produkts mit einem erheblichen finanziellen Risiko verbunden.
Entscheidungsträger sollten sich überlegen, ob das Unternehmen mit dieser Unsicherheit und der Möglichkeit von unterdurchschnittlichen Gewinnen klarkommt.
Außerdem empfehlen wir dir , Visualisierungen wie Histogramme zu erstellen, um die Ergebnisse der Simulationen besser zu verstehen. Das ist zwar optional, aber echt hilfreich.
Techniken zur Verbesserung von Excel-Monte-Carlo-Simulationen
Wenn du die gleiche Simulation wie oben nochmal machst, kannst du einen kleinen Unterschied in den Berechnungen sehen, wie unten gezeigt:
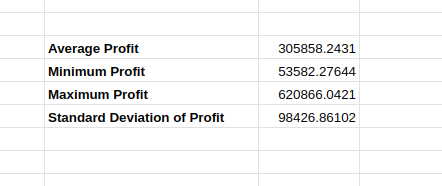
Unterschiedliche Simulationsergebnisse.
Das liegt daran, dass sich die Werte der ursprünglichen Simulation zwischen den Iterationen ändern können, was die resultierenden Schätzungen beeinflusst. Auch wenn die Abweichung gering ist, macht sich bei den Entscheidungsträgern doch ein bisschen Sorge um die Genauigkeit und Zuverlässigkeit der Simulation breit, wenn sich der geschätzte Wert ändert.
Schauen wir uns ein paar fortgeschrittene Techniken an, mit denen wir die Genauigkeit und Zuverlässigkeit der Simulationen verbessern können.
Mehr Simulationen machen
Wenn man mehr Simulationen macht, kann man zufällige Schwankungen ausgleichen und bekommt eine stabilere und genauere Schätzung der Ergebnisse.
Für das obige Beispiel können wir die Anzahl der Simulationsläufe erhöhen (z. B. von 1.000 auf 10.000 oder mehr), vor allem wenn wir es mit stark variierenden Parametern zu tun haben.
Die richtige Anzahl an Simulationen hängt von ein paar Sachen ab.
Je komplizierter das Modell ist (also je mehr Variablen es hat und je mehr sie miteinander interagieren), desto mehr Simulationen braucht man normalerweise, um alle möglichen Ergebnisse zu erfassen und sicherzustellen, dass die Ergebnisse nicht nur Zufall sind.
Wenn die Eingaben sehr unterschiedlich sind oder stark verzerrt, braucht man mehr Simulationen, um die Randwerte (Extremwerte) der Ergebnisverteilungen genau zu schätzen.
Für genauere Analysen, vor allem im Finanzwesen oder Risikomanagement, ist es nicht ungewöhnlich, 10.000 bis 100.000 Simulationen durchzuführen. Dieser Bereich wird normalerweise benutzt, um zuverlässige Ergebnisse in verschiedenen Szenarien und bei unterschiedlichen Eingaben zu garantieren. Wie wir schon gesagt haben, ist Excel für so große Analysen nicht immer das beste Tool, sondern eher R oder Python.
Die Eingabeverteilungen optimieren
Wie genau die Simulationen sind, hängt echt davon ab, wie gut die eingegebenen Wahrscheinlichkeitsverteilungen die echten Unsicherheiten und das Verhalten der zugrunde liegenden Variablen zeigen. In unserem Beispiel oben haben wir angenommen, dass Nachfrage und Kosten normal verteilt sind und der Verkaufspreis gleichmäßig verteilt ist.
Außerdem könnten wir umfassendere historische Daten analysieren, um die Verteilungen besser zu parametrisieren. Mit Hilfe von Expertenwissen können wir das Verhalten von Kosten, Umsatz und Nachfrage in Bezug auf externe Faktoren besser verstehen. Wir können auch Distributionen wie log-normal, Beta oder Gamma nutzen oder eigene Distributionen auf Basis empirischer Daten erstellen.
Eine Sensitivitätsanalyse machen
Diese Analyse wird gemacht, um zu verstehen, welche Eingabevariablen den größten Einfluss auf das Ergebnis haben, indem man jede Eingabe systematisch verändert, während die anderen konstant bleiben.
In unserem Beispiel oben können wir zwei Variablen konstant halten und die Verteilung einer Variablen ändern, um die Änderungen in den Schätzungen zu verstehen. Mach dann dasselbe mit den beiden anderen Variablen, eine nach der anderen. Letztendlich hilft diese Technik dabei, zu verstehen, auf welche Variable man sich konzentrieren muss, um die Genauigkeit zu verbessern.
Wenn man die oben genannten Techniken immer wieder anwendet und die Ergebnisse analysiert, kann man genauere und zuverlässigere Ergebnisse bekommen.
Fazit
In diesem Tutorial hast du die Monte-Carlo-Simulation und die dazugehörigen statistischen Konzepte kennengelernt. Nachdem die wichtigen Excel-Funktionen erklärt wurden, hat das Tutorial eine Schritt-für-Schritt-Anleitung gezeigt, wie man die Monte-Carlo-Simulation in Excel anhand eines echten Beispiels umsetzt.
Zum Schluss hast du ein paar bewährte Methoden und fortgeschrittene Techniken kennengelernt, damit deine Ergebnisse genauer und zuverlässiger werden.
Wenn du besonders daran interessiert bist, die oben genannte Monte-Carlo-Simulation mit anderen Tools wie Python oder R umzusetzen, könnten diese beiden Ressourcen nützlich sein:
Wenn du lieber beim bekannten Microsoft Excel bleiben und deine Kenntnisse mit diesem weit verbreiteten Tool verbessern möchtest, solltest du dir unseren Lernpfad „Excel-Grundlagen” ansehen.
Bringe deine Karriere mit Excel voran
Erwerbe die Fähigkeiten, um Excel optimal zu nutzen - keine Erfahrung erforderlich.

Als Senior Data Scientist konzipiere, entwickle und implementiere ich umfangreiche Machine-Learning-Lösungen, um Unternehmen dabei zu helfen, bessere datengestützte Entscheidungen zu treffen. Als Data-Science-Autorin teile ich Erfahrungen, Karrieretipps und ausführliche praktische Anleitungen.

