Cours
Les méthodes de Monte-Carlo, initialement nommées d'après le casino de Monte-Carlo à Monaco, sont largement utilisées dans des domaines tels que la finance, l'ingénierie, la chaîne d'approvisionnement et les sciences pour modéliser des phénomènes dont les données d'entrée présentent une incertitude significative.
Cependant, qu'est-ce que la simulation de Monte-Carlo ? Comment cela fonctionne-t-il ? Et comment puis-je mettre en œuvre la simulation et analyser les résultats ?
Ce tutoriel vous présentera la simulation Monte Carlo et les concepts statistiques pertinents qui sous-tendent cette technique. Nous mettrons également en œuvre la simulation de Monte Carlo dans Excel, vous familiarisant ainsi avec les fonctions intégrées pertinentes d'Excel.
Enfin, ce tutoriel vous fournira les meilleures pratiques, des techniques avancées et des ressources supplémentaires, ce qui en fait un guide complet pour tout apprendre sur la simulation Monte Carlo dans Microsoft Excel.
Qu'est-ce que la simulation de Monte Carlo ?
La simulation de Monte Carlo est une technique mathématique utilisée pour modéliser la probabilité de différents résultats dans un processus qui ne peut être facilement prédit en raison de l'intervention de variables aléatoires.
Il s'agit d'un outil puissant pour appréhender l'impact du risque et de l'incertitude dans divers domaines. Cette méthode repose sur des échantillonnages aléatoires répétés afin de simuler le comportement de systèmes et de processus complexes.
Le problème est d'abord modélisé par une distribution de probabilité pour chaque variable présentant une incertitude inhérente. Un grand nombre d'échantillons aléatoires sont ensuite prélevés à partir de ces distributions de probabilité, et ces échantillons sont utilisés pour calculer les résultats. Ce processus est répété à plusieurs reprises afin de créer une distribution des résultats possibles, qui peut être analysée statistiquement pour fournir des prévisions sur le comportement d'un système.
En termes simples, La simulation de Monte Carlo est une technique qui prédit le comportement de systèmes complexes en simulant leurs résultats à plusieurs reprises à l'aide de valeurs aléatoires. Il comporte plusieurs étapes :
- Incertitude du modèle : Définissez comment chaque variable peut varier à l'aide de distributions de probabilité.
- Échantillonnage aléatoire : Veuillez sélectionner des valeurs aléatoires pour ces variables en fonction de leurs distributions.
- Simuler les résultats : Veuillez utiliser ces valeurs pour simuler le comportement du système.
- Analyser les résultats : Répétez le processus à plusieurs reprises afin d'obtenir une gamme de résultats possibles, puis analysez-les pour prédire les scénarios les plus probables.
Ensuite, nous approfondirons nos connaissances de base sur la simulation de Monte Carlo en explorant certains concepts statistiques pertinents.
Variables aléatoires et distributions de Monte Carlo
Les variables aléatoires et leurs distributions de probabilité associées sont fondamentales pour la simulation de Monte Carlo, car elles fournissent le cadre mathématique permettant de modéliser et de simuler le caractère aléatoire et la variabilité inhérents aux systèmes complexes.
Variables aléatoires
Une variable aléatoire est une variable dont les valeurs sont les résultats d'un phénomène aléatoire.
Les variables aléatoires sont classées en deux types :
- Variables aléatoires discrètes : Ces variables prennent un nombre dénombrable de valeurs distinctes. Dans les simulations, les variables discrètes peuvent modéliser des scénarios tels que le nombre d'articles défectueux dans un lot, le nombre d'arrivées de clients par heure ou d'autres événements quantifiables.
- Variables aléatoires continues : Ces variables peuvent prendre n'importe quelle valeur dans un intervalle continu. Les variables continues sont utilisées pour les simulations portant sur des mesures physiques ou des durées.
Les variables aléatoires sont utilisées dans les simulations car elles intègrent l'incertitude que les techniques de Monte Carlo sont conçues pour explorer et quantifier.
Distributions de probabilité
Les distributions de probabilité décrivent la manière dont les probabilités sont réparties entre les valeurs d'une variable aléatoire.
Les distributions de probabilité sont utilisées dans la simulation de Monte Carlo pour définir comment différentes entrées ou différents scénarios sont susceptibles de se comporter, ce qui est essentiel pour une modélisation et une prise de décision précises.
La distribution normale est la distribution la plus couramment utilisée en statistiques et en simulations, car de nombreux phénomènes naturels et artificiels ont tendance à suivre cette distribution en raison du théorème de la limite centrale.
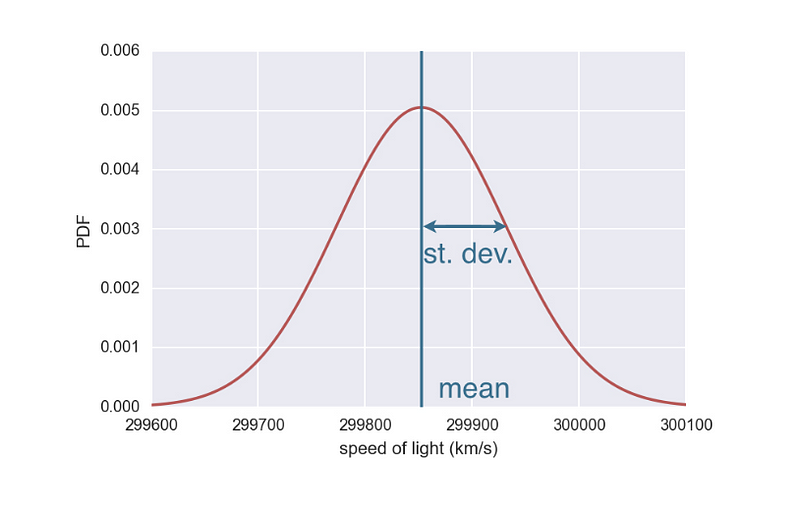
Distribution normale (Source)
La distribution normale est utilisée pour modéliser des variables influencées par de nombreux effets mineurs et indépendants, tels que les erreurs de mesure ou les rendements boursiers.
D'autres distributions de probabilité sont les distributions uniformes, utilisées lorsque tous les résultats d'une plage donnée ont la même probabilité, une hypothèse courante dans les simulations lorsqu'aucune donnée préalable n'est disponible, et les distributions binomiales, utilisées pour modéliser des scénarios avec deux résultats possibles (réussite/échec) dans une série d'expériences, telles que les tests de réussite/échec ou les contrôles de qualité.
Maintenant que nous avons compris les concepts et la théorie qui sous-tendent les simulations de Monte Carlo, passons à la mise en œuvre.
Apprendre les bases d'Excel
Pourquoi utiliser Excel pour la simulation de Monte Carlo ?
Une fois que vous avez décidé de mettre en œuvre une simulation Monte Carlo, vous disposez de plusieurs outils, tels qu'Excel, Python, R, SAS et MATLAB, pour vous aider dans vos simulations.
Le facteur le plus important à prendre en compte, en particulier lors de la première utilisation de la simulation de Monte Carlo, est votre niveau de familiarité avec l'outil. Excel est l'un des outils les plus utilisés dans le monde des affaires, ce qui signifie que de nombreuses personnes connaissent déjà ses fonctions de base. Cela réduit le temps de formation et élimine la nécessité d'apprendre à utiliser un nouveau logiciel à partir de zéro.
Excel propose également des outils simples d'utilisation pour créer des tableaux et des graphiques, qui peuvent être utiles pour visualiser les résultats des simulations. De plus, plusieurs compléments performants sont disponibles pour Excel, améliorant ainsi sa capacité à effectuer des simulations Monte Carlo complexes.
Il convient toutefois de noter que pour les simulations plus avancées, en particulier celles qui nécessitent le traitement de grands ensembles de données ou l'exécution d'un nombre très élevé de simulations, des outils plus spécialisés que Excel pourraient s'avérer plus appropriés.
Fonctions Excel essentielles pour Monte Carlo
Ensuite, nous examinerons deux fonctions Excel essentielles : RAND() et NORM.INV(), en abordant leur syntaxe, leurs paramètres et leurs cas d'utilisation courants. Ces fonctions permettent de générer des nombres aléatoires et de définir des distributions de probabilité, qui sont des aspects fondamentaux de toute simulation.
La fonction RAND()
RAND() génère un nombre aléatoire supérieur ou égal à 0 et inférieur à 1. Les nombres sont répartis uniformément, ce qui signifie que tout nombre compris dans la plage spécifiée a autant de chances d'apparaître.
La syntaxe pour RAND() est la suivante :
RAND()La fonction ` RAND() ` ne nécessite aucun argument. Il est utilisé simplement comme RAND().
Dans le cadre de la simulation de Monte Carlo, RAND() peut être utilisé pour simuler la survenue d'événements aléatoires ou pour faire varier les entrées de votre modèle.
La fonction NORM.INV()
Alors que la fonction ` RAND() ` génère des nombres aléatoires uniformes, la fonction ` NORM.INV() ` est utilisée pour générer des nombres aléatoires à partir d'une distribution normale, ce qui est une exigence courante dans une simulation de Monte Carlo. Cette fonction renvoie l'inverse de la distribution cumulative normale pour une moyenne et un écart type spécifiés.
La syntaxe de la fonction d'NORM.INV() est la suivante :
NORM.INV(probability, mean, standard_deviation)Les paramètres sont les suivants :
-
probability: Une probabilité correspondant à la distribution normale, qui doit être une valeur comprise entre 0 et 1. Ceci est généralement généré par la fonctionRAND(). -
mean: La moyenne arithmétique de la distribution normale. -
standard_deviation: L'écart type de la distribution normale, une mesure de la dispersion des nombres autour de la moyenne.
NORM.INV() RAND() La fonction « normal_distribution» est utilisée pour convertir des nombres aléatoires uniformément distribués provenant de la fonction « random_distribution » en nombres qui suivent une distribution normale spécifiée. Cela s'avère utile pour modéliser des variables qui devraient présenter une variabilité naturelle suivant une courbe normale.
Maintenant que nous disposons de tous les éléments constitutifs, fonctions et concepts nécessaires à une simulation Monte Carlo, nous allons en mettre une en œuvre dans Microsoft Excel.
Mise en œuvre de la simulation de Monte Carlo dans Microsoft Excel : Un exemple
Imaginez que vous soyez analyste de données dans une entreprise dynamique spécialisée dans l'électronique grand public et que vous ayez été chargé d'évaluer la viabilité financière du lancement d'un nouveau bracelet connecté.
Le marché de ces appareils est concurrentiel et la demande des consommateurs peut être très variable, influencée par les tendances saisonnières, l'efficacité du marketing et les actions des concurrents. De plus, les coûts liés à la fabrication de ces dispositifs sont sujets à des fluctuations en raison des variations des coûts des matériaux et des incertitudes liées à la chaîne d'approvisionnement.
Vous avez décidé d'utiliser la simulation de Monte Carlo dans Excel pour relever ces défis. Vous estimez que cette approche vous aidera à estimer la rentabilité potentielle dans différents scénarios, permettant ainsi à l'entreprise de prendre des décisions éclairées en matière de stratégies de tarification, de volumes de production et d'investissements marketing.
Vous avez également analysé les données historiques relatives au lancement de produits similaires et aux études de marché dans le secteur de l'électronique grand public. À partir de cette analyse, vous avez déterminé certains indicateurs qui serviront de base à votre simulation :
- Une demande moyenne de 10 000 unités pour les nouveaux appareils au cours de la première année suivant leur lancement, avec un écart type de 2 000 unités, reflétant l'incertitude quant à l'adoption par les consommateurs.
- Le prix de vente unitaire varie généralement entre 50 et 70 dollars, en fonction de la concurrence et de la saturation du marché.
- Le coût unitaire, influencé par la volatilité des prix des matériaux et l'efficacité de la fabrication, s'élève en moyenne à 30 dollars par unité, avec un écart type de 5 dollars.
Ces données historiques constituent les hypothèses sous-jacentes de vos paramètres de simulation, contribuant ainsi à créer une simulation qui reflète plus fidèlement les conditions actuelles du marché.
Les étapes à suivre pour mettre en œuvre la simulation de Monte Carlo dans cet exemple particulier sont les suivantes :
Étape 1 : Veuillez configurer votre feuille Excel.
Tout d'abord, veuillez préparer votre feuille de calcul Excel afin d'inclure des colonnes pour chaque variable et une colonne pour le bénéfice calculé.
Voici à quoi cela ressemblerait initialement :
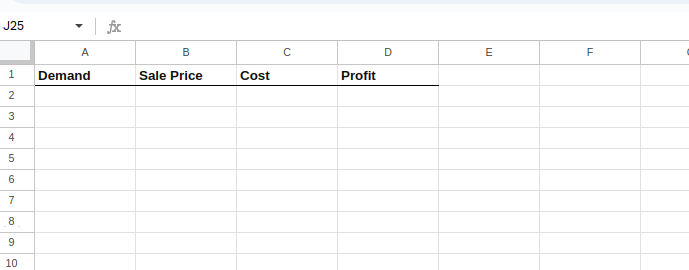
Configuration de la feuille Excel.
Étape 2 : Formules de saisie pour les variables
Dans chaque ligne, vous saisirez des formules pour générer des valeurs aléatoires pour la demande, le prix de vente et le coût en fonction des distributions que vous avez identifiées :
- Demande : Distribution normale (moyenne = 10 000 unités, écart type = 2 000 unités)
- Prix de vente : Distribution uniforme (50 $ à 70 $)
- Coût : Distribution normale (moyenne = 30 $, écart-type = 5 $)
Pour saisir ces formules une par une, veuillez sélectionner la cellule A2 et saisir ce qui suit :
=NORM.INV(RAND(), 10000, 2000)L'équation ci-dessus génère une distribution normale avec une moyenne et un écart-type donnés, comme indiqué ci-dessous :
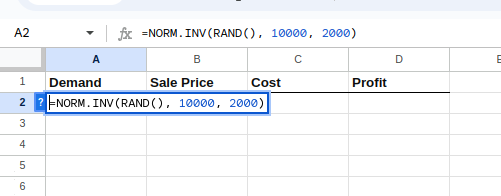
Création de la distribution pour répondre à la demande.
Ensuite, veuillez sélectionner la cellule B2 et saisir ce qui suit :
=50 + (70-50) * RAND()L'équation ci-dessus génère une distribution uniforme entre 50 $ et 70 $ pour le prix de vente, comme indiqué ci-dessous :
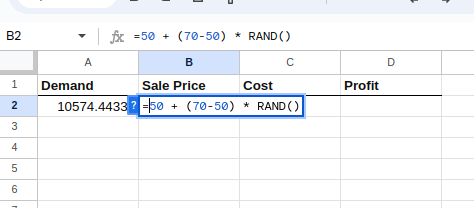
Création de la distribution pour le prix de vente.
Veuillez sélectionner la cellule C2 et saisir ce qui suit :
=NORM.INV(RAND(), 30, 5)L'équation ci-dessus, similaire à l'équation de la demande, crée une distribution normale avec une moyenne et un écart-type donnés, comme indiqué ci-dessous :
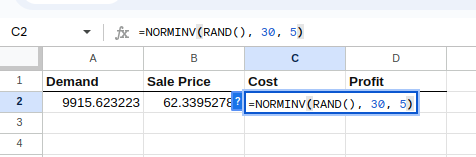
Création de la distribution des coûts.
Étape 3 : Veuillez calculer la variable dépendante.
Veuillez maintenant calculer le bénéfice, qui est la variable dépendante, pour chaque simulation à l'aide de la formule de la colonne D :
=(B2 - C2) * A2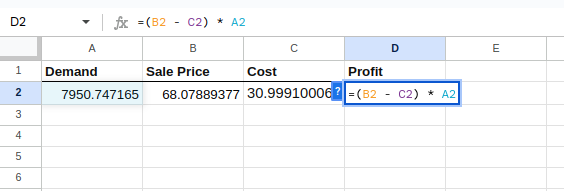
Calculer le bénéfice.
Étape 4 : Remplissez pour simuler plusieurs scénarios
Ce que nous avons réalisé jusqu'à présent consiste à créer une simulation unique. Étendons cela à plusieurs simulations, disons un millier.
Veuillez sélectionner les cellules A2 à D2 et faire glisser la poignée de remplissage (un petit carré situé en bas à droite de la sélection) vers le bas afin de remplir les formules sur autant de lignes que vous souhaitez simuler (par exemple, 1 000 lignes pour 1 000 simulations).
Cela ressemblera à ceci :
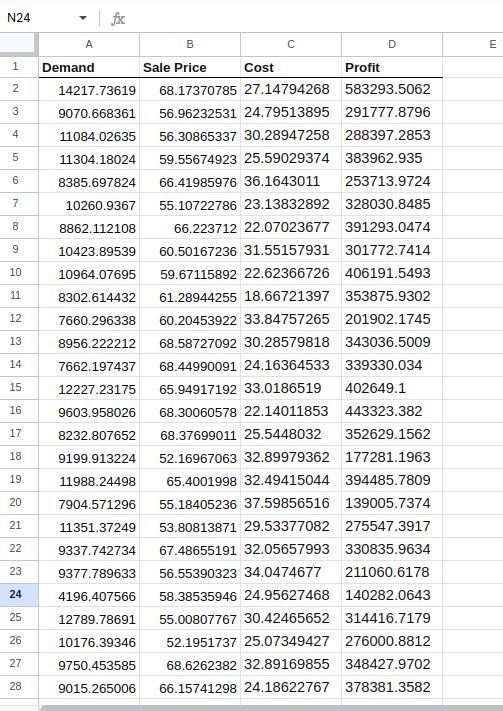
Réalisation des simulations.
Étape 5 : Veuillez analyser les résultats.
Après avoir exécuté les simulations, vous pouvez analyser les résultats à l'aide de fonctions statistiques telles que min, max, moyenne et écarts types. N'hésitez pas à consulter rapidement l'aide-mémoire Excel pour vous rafraîchir la mémoire sur les fonctions Excel intégrées que nous utiliserons ensuite.
Pour déterminer le bénéfice mensuel moyen prévu, veuillez saisir la formule suivante dans une cellule, par exemple G6 :
=AVERAGE(D2:D1001)Pour déterminer le bénéfice minimum attendu chaque mois, veuillez saisir la formule suivante dans une cellule, par exemple G7 :
=MIN(D2:D1001)Pour déterminer le bénéfice maximal attendu chaque mois, veuillez saisir la formule suivante dans une cellule, par exemple G8 :
=MAX(D2:D1001)Pour déterminer l'écart type du bénéfice, veuillez saisir la formule suivante dans une cellule, par exemple G9 :
=STDEV.P(D2:D1001)Une fois exécutée, la feuille Excel devrait ressembler à ceci :
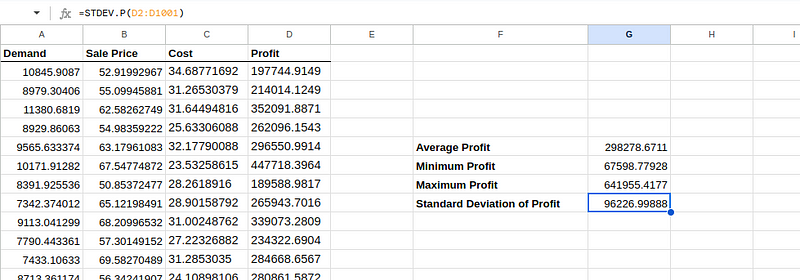
Analyse des résultats de la simulation.
Nous pouvons interpréter les résultats estimés et les implications pour le lancement du produit comme suit :
- Le chiffre moyen des bénéfices représente les bénéfices attendus du lancement du nouveau tracker d'activité physique. Cela indique qu'en moyenne, chaque simulation prévoit que nous pourrions réaliser un bénéfice d'environ 298 278,67 $. Cette valeur est utile en tant qu'estimation centrale de la rentabilité selon les hypothèses données.
- Un bénéfice minimal de 67 598,78 $ est le bénéfice le plus bas observé dans toutes nos simulations. Il indique le scénario le plus défavorable selon les hypothèses de votre modèle, qui reste rentable mais nettement moins que la moyenne. Cela pourrait être dû à une demande particulièrement faible ou à des conditions de coûts défavorables dans cette simulation spécifique.
- Un bénéfice maximal de 641 955,42 $ représente le scénario le plus favorable, dans lequel la demande et les prix étaient probablement les plus élevés et les coûts les plus bas parmi toutes les simulations. Cela démontre le potentiel de hausse si les conditions s'avèrent très favorables.
Compte tenu de l'écart important entre les bénéfices minimums et maximums et de l'écart type considérable, le lancement du nouveau produit comporte un risque financier important.
Les décideurs doivent déterminer si l'entreprise est à l'aise avec ce niveau d'incertitude et la possibilité de bénéfices inférieurs à la moyenne.
De plus, bien que cela soit facultatif, nous vous encourageons à créer des visualisations telles que des histogrammes afin d'avoir une compréhension visuelle des résultats des simulations.
Techniques pour améliorer les simulations Monte Carlo dans Excel
Lorsque vous relancez la même simulation que ci-dessus, vous pouvez observer une légère différence dans les calculs, comme indiqué ci-dessous :
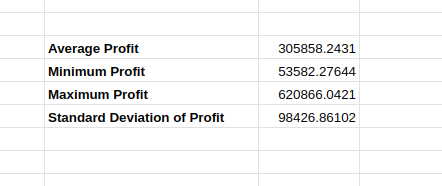
Résultats de simulation variables.
En effet, les valeurs de la simulation initiale peuvent varier d'une itération à l'autre, ce qui influe sur les estimations obtenues. Bien que la variation soit minime, lorsque la valeur estimée change, les décideurs s'interrogent sur la précision et la fiabilité de la simulation.
Nous allons examiner quelques techniques avancées que nous pourrions utiliser pour améliorer la précision et la fiabilité des simulations.
Augmenter le nombre de simulations
L'exécution d'un plus grand nombre de simulations permet de lisser les fluctuations aléatoires et fournit une estimation plus stable et plus précise des résultats.
Dans l'exemple ci-dessus, nous pouvons augmenter le nombre de simulations (par exemple, de 1 000 à 10 000 ou plus), en particulier lorsque nous traitons des paramètres très variables.
La détermination du nombre « adéquat » de simulations dépend de plusieurs facteurs.
Plus le modèle est complexe (c'est-à-dire plus il comporte de variables et plus l'éventail de leurs interactions est large), plus il est généralement nécessaire de réaliser de simulations pour saisir tous les résultats possibles et s'assurer que les résultats ne sont pas le fruit du hasard.
Si les données d'entrée présentent une grande variabilité ou sont fortement asymétriques, il sera nécessaire de réaliser davantage de simulations afin d'estimer avec précision les extrémités (valeurs extrêmes) des distributions des résultats.
Pour des analyses plus approfondies, notamment dans le domaine de la finance ou de la gestion des risques, il n'est pas rare de réaliser entre 10 000 et 100 000 simulations. Cette plage est généralement utilisée pour garantir des résultats fiables dans divers scénarios et avec différentes entrées. Bien entendu, comme nous l'avons mentionné précédemment, pour une analyse à si grande échelle, Excel n'est pas toujours l'outil le plus approprié, R ou Python étant plus adaptés.
Amélioration des distributions d'entrée
La précision des simulations dépend en grande partie de la capacité des distributions de probabilité saisies à refléter fidèlement l'incertitude et le comportement réels des variables sous-jacentes. Dans l'exemple ci-dessus, nous avons supposé une distribution normale pour la demande et les coûts, et une distribution uniforme pour le prix de vente.
De plus, nous pourrions analyser des données historiques plus complètes afin de mieux paramétrer les distributions. Nous pouvons mieux appréhender les comportements liés aux coûts, aux ventes et à la demande en fonction de facteurs externes, en nous appuyant sur les avis d'experts du domaine. Nous pouvons également envisager d'utiliser des distributions telles que log-normale, bêta ou gamma, ou de créer des distributions personnalisées basées sur des données empiriques.
Réalisation d'une analyse de sensibilité
Cette analyse est effectuée afin de déterminer quelles variables d'entrée ont l'impact le plus significatif sur le résultat, en faisant varier systématiquement chaque entrée tout en maintenant les autres constantes.
Dans notre exemple ci-dessus, nous pouvons maintenir deux variables constantes et modifier la distribution de l'une d'entre elles afin de comprendre les changements dans les estimations. Ensuite, veuillez répéter le même processus pour les deux variables restantes, une par une. En fin de compte, cette technique permet de déterminer sur quelle variable concentrer les efforts afin d'améliorer la précision.
L'utilisation répétée des techniques ci-dessus et l'analyse des résultats peuvent conduire à des résultats plus précis et plus fiables.
Conclusion
Ce tutoriel vous a présenté la simulation de Monte Carlo et les concepts statistiques associés. Après avoir présenté les fonctions Excel pertinentes, le tutoriel a fourni un guide étape par étape pour mettre en œuvre la simulation de Monte Carlo dans Excel à l'aide d'un exemple concret.
Enfin, vous avez découvert certaines bonnes pratiques et techniques avancées pour garantir des résultats plus précis et fiables.
Si vous êtes particulièrement intéressé par la mise en œuvre de la simulation de Monte Carlo ci-dessus à l'aide d'autres outils tels que Python ou R, ces deux ressources pourraient vous être utiles :
Si vous préférez rester fidèle à Microsoft Excel et souhaitez perfectionner vos compétences dans l'utilisation de cet outil largement répandu, nous vous invitons à consulter notre cursus « Excel Fundamentals ».
Faites progresser votre carrière avec Excel
Acquérir les compétences nécessaires pour optimiser Excel - aucune expérience n'est requise.

En tant que data scientist senior, je conçois, développe et déploie des solutions d'apprentissage automatique à grande échelle pour aider les entreprises à prendre de meilleures décisions basées sur les données. En tant que rédacteur spécialisé dans la science des données, je partage mes apprentissages, mes conseils de carrière et des tutoriels pratiques approfondis.