Curso
Ejecuta y edita el código de este tutorial en línea
Ejecutar códigoIntroducción al ACP en Python
El Análisis de Componentes Principales (ACP) es una técnica lineal de reducción de la dimensionalidad que puede utilizarse para extraer información de un espacio de alta dimensión proyectándola en un subespacio de dimensión inferior. Intenta conservar las partes esenciales que tienen más variación de los datos y eliminar las partes no esenciales con menos variación.
Las dimensiones no son más que características que representan los datos. Por ejemplo, una imagen de 28 X 28 tiene 784 elementos de imagen (píxeles) que son las dimensiones o características que en conjunto representan esa imagen.
Una cosa importante que hay que tener en cuenta sobre el ACP es que es una técnica de reducción de la dimensionalidad no supervisada, puedes agrupar los puntos de datos similares basándote en la correlación de características entre ellos sin ningún tipo de supervisión (o etiquetas), ¡y aprenderás a conseguirlo de forma práctica utilizando Python en secciones posteriores de este tutorial!
Según Wikipedia, el ACP es un procedimiento estadístico que utiliza una transformación ortogonal para convertir un conjunto de observaciones de variables posiblemente correlacionadas (entidades cada una de las cuales adopta diversos valores numéricos) en un conjunto de valores de variables linealmente no correlacionadas denominadas componentes principales.
Nota: Características, Dimensiones y Variables se refieren a lo mismo. Verás que se utilizan indistintamente.
Practica el Análisis de Componentes Principales (ACP) en Python con este ejercicio práctico.
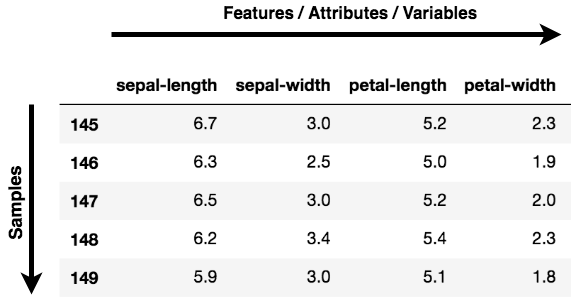
¿Dónde puedes aplicar la PCA?
-
Visualización de datos: Cuando se trabaja en cualquier problema relacionado con los datos, el reto en el mundo actual es el enorme volumen de datos, y las variables/características que definen esos datos. Para resolver un problema en el que los datos son la clave, necesitas una amplia exploración de los datos, como averiguar cómo se correlacionan las variables o comprender la distribución de unas pocas variables. Teniendo en cuenta que hay un gran número de variables o dimensiones a lo largo de las cuales se distribuyen los datos, la visualización puede ser un reto y casi imposible.
De ahí que el ACP pueda hacerlo por ti, ya que proyecta los datos en una dimensión inferior, permitiéndote así visualizarlos en un espacio 2D o 3D a simple vista.
-
Acelerar un algoritmo de machine learning (ML): Como la idea principal del PCA es la reducción de la dimensionalidad, puedes aprovecharla para acelerar el tiempo de entrenamiento y prueba de tu algoritmo de machine learning si tus datos tienen muchas características y el aprendizaje del algoritmo de ML es demasiado lento.
A un nivel abstracto, tomas un conjunto de datos que tiene muchas características y lo simplificas seleccionando unas pocas Principal Components de las características originales.
¿Qué es un Componente Principal?
Los componentes principales son la clave del ACP; representan lo que hay bajo el capó de tus datos. En términos sencillos, cuando los datos se proyectan en una dimensión inferior (supongamos tres dimensiones) desde un espacio superior, las tres dimensiones no son más que los tres Componentes Principales que captan (o contienen) la mayor parte de la varianza (información) de tus datos.
Los componentes principales tienen dirección y magnitud. La dirección representa a través de qué ejes principales se extienden mayoritariamente los datos o tienen más varianza, y la magnitud significa la cantidad de varianza que el Componente Principal capta de los datos cuando se proyecta sobre ese eje. Los componentes principales son una línea recta, y el primer componente principal contiene la mayor varianza de los datos. Cada componente principal posterior es ortogonal al anterior y tiene una varianza menor. De este modo, dado un conjunto de x variables correlacionadas sobre y muestras, se obtiene un conjunto de u componentes principales no correlacionados sobre las mismas y muestras.
La razón por la que consigues componentes principales no correlacionados a partir de las características originales es que las características correlacionadas contribuyen al mismo componente principal, reduciendo así las características de los datos originales en componentes principales no correlacionados; cada uno de ellos representa un conjunto diferente de características correlacionadas con distintas cantidades de variación.
Cada componente principal representa un porcentaje de la variación total captada de los datos.
En el tutorial de hoy, aplicarás principalmente el ACP en los dos casos de uso:
Data VisualizationSpeeding ML algorithm
Para realizar las dos tareas anteriores, utilizarás dos famosos conjuntos de datos de Cáncer de Mama (numérico) y CIFAR - 10 (imagen).
Comprender los datos
Antes de seguir adelante y cargar los datos, ¡es bueno que comprendas y veas los datos con los que vas a trabajar!
Cáncer de mama
El conjunto de datos Cáncer de Mama es un dato multivariante de valor real que consta de dos clases, donde cada clase significa si una paciente tiene cáncer de mama o no. Las dos categorías son: malignas y benignas.
La clase maligna tiene 212 muestras, mientras que la clase benigna tiene 357 muestras.
Tiene 30 características compartidas por todas las clases: radio, textura, perímetro, área, suavidad, dimensión fractal, etc.
Puedes descargar el conjunto de datos sobre el cáncer de mama desde aquí, o más bien una forma fácil es cargándolo con la ayuda de la función sklearn biblioteca.
CIFAR - 10
El conjunto de datos CIFAR-10 (Instituto Canadiense de Investigación Avanzada) consta de 60000 imágenes en color de 32x32x3 cada una, con diez clases y 6000 imágenes por categoría.
El conjunto de datos consta de 50000 imágenes de entrenamiento y 10000 imágenes de prueba.
Las clases del conjunto de datos son avión, automóvil, pájaro, gato, ciervo, perro, rana, caballo, barco y camión.
Puedes descargar el conjunto de datos CIFAR desde aquí, o también puedes cargarlo sobre la marcha con la ayuda de una biblioteca de aprendizaje profundo como Keras.
Exploración de datos
Ahora cargarás y analizarás la Breast Cancer y CIFAR-10 conjuntos de datos. Ahora ya tienes una idea de la dimensionalidad de ambos conjuntos de datos.
Exploremos rápidamente ambos conjuntos de datos.
Exploración de datos sobre el cáncer de mama
Exploremos primero la Breast Cancer conjunto de datos.
Utilizarás sklearn's módulo datasets e importa el Breast Cancer conjunto de datos a partir de él.
from sklearn.datasets import load_breast_cancer
load_breast_cancer te dará tanto las etiquetas como los datos. Para obtener los datos, llamarás a .data y para obtener las etiquetas .target.
Los datos tienen 569 muestras con treinta características, y cada muestra tiene asociada una etiqueta. Hay dos etiquetas en este conjunto de datos.
breast = load_breast_cancer()
breast_data = breast.data
Comprobemos la forma de los datos.
breast_data.shape
(569, 30)
Aunque para este tutorial no necesites las etiquetas, para una mejor comprensión, vamos a cargar las etiquetas y comprobar la forma.
breast_labels = breast.target
breast_labels.shape
(569,)
Ahora importarás numpy ya que vas a remodelar el breast_labels para concatenarla con la breast_data para que finalmente puedas crear un DataFrame que tendrá tanto los datos como las etiquetas.
import numpy as np
labels = np.reshape(breast_labels,(569,1))
Después de reshaping las etiquetas, podrás concatenate los datos y las etiquetas a lo largo del segundo eje, lo que significa que la forma final de la matriz será 569 x 31.
final_breast_data = np.concatenate([breast_data,labels],axis=1)
final_breast_data.shape
(569, 31)
Ahora importarás pandas para crear el DataFrame de los datos finales para representar los datos de forma tabular.
import pandas as pd
breast_dataset = pd.DataFrame(final_breast_data)
¡Vamos a imprimir rápidamente las características que hay en el conjunto de datos del cáncer de mama!
features = breast.feature_names
features
array(['mean radius', 'mean texture', 'mean perimeter', 'mean area',
'mean smoothness', 'mean compactness', 'mean concavity',
'mean concave points', 'mean symmetry', 'mean fractal dimension',
'radius error', 'texture error', 'perimeter error', 'area error',
'smoothness error', 'compactness error', 'concavity error',
'concave points error', 'symmetry error',
'fractal dimension error', 'worst radius', 'worst texture',
'worst perimeter', 'worst area', 'worst smoothness',
'worst compactness', 'worst concavity', 'worst concave points',
'worst symmetry', 'worst fractal dimension'], dtype='<U23')
Si observas en el features matriz, el label Falta el campo Por lo tanto, tendrás que añadirlo manualmente a la casilla features ya que estarás equiparando esta matriz con los nombres de las columnas de tu breast_dataset marco de datos.
features_labels = np.append(features,'label')
¡Estupendo! Ahora incrustarás los nombres de las columnas en el breast_dataset marco de datos.
breast_dataset.columns = features_labels
Vamos a imprimir las primeras filas de la trama de datos.
breast_dataset.head()
| radio medio | textura media | perímetro medio | superficie media | suavidad media | compacidad media | concavidad media | puntos cóncavos medios | simetría media | dimensión fractal media | ... | peor textura | peor perímetro | peor zona | peor suavidad | peor compacidad | peor concavidad | peores puntos cóncavos | peor simetría | peor dimensión fractal | etiqueta | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 17.99 | 10.38 | 122.80 | 1001.0 | 0.11840 | 0.27760 | 0.3001 | 0.14710 | 0.2419 | 0.07871 | ... | 17.33 | 184.60 | 2019.0 | 0.1622 | 0.6656 | 0.7119 | 0.2654 | 0.4601 | 0.11890 | 0.0 |
| 1 | 20.57 | 17.77 | 132.90 | 1326.0 | 0.08474 | 0.07864 | 0.0869 | 0.07017 | 0.1812 | 0.05667 | ... | 23.41 | 158.80 | 1956.0 | 0.1238 | 0.1866 | 0.2416 | 0.1860 | 0.2750 | 0.08902 | 0.0 |
| 2 | 19.69 | 21.25 | 130.00 | 1203.0 | 0.10960 | 0.15990 | 0.1974 | 0.12790 | 0.2069 | 0.05999 | ... | 25.53 | 152.50 | 1709.0 | 0.1444 | 0.4245 | 0.4504 | 0.2430 | 0.3613 | 0.08758 | 0.0 |
| 3 | 11.42 | 20.38 | 77.58 | 386.1 | 0.14250 | 0.28390 | 0.2414 | 0.10520 | 0.2597 | 0.09744 | ... | 26.50 | 98.87 | 567.7 | 0.2098 | 0.8663 | 0.6869 | 0.2575 | 0.6638 | 0.17300 | 0.0 |
| 4 | 20.29 | 14.34 | 135.10 | 1297.0 | 0.10030 | 0.13280 | 0.1980 | 0.10430 | 0.1809 | 0.05883 | ... | 16.67 | 152.20 | 1575.0 | 0.1374 | 0.2050 | 0.4000 | 0.1625 | 0.2364 | 0.07678 | 0.0 |
5 filas × 31 columnas
Como las etiquetas originales están en 0,1 cambiarás las etiquetas a benign y malignant utilizando .replace . Utilizarás inplace=True que modificará el marco de datos breast_dataset.
breast_dataset['label'].replace(0, 'Benign',inplace=True)
breast_dataset['label'].replace(1, 'Malignant',inplace=True)
Imprimamos las últimas filas del archivo breast_dataset.
breast_dataset.tail()
| radio medio | textura media | perímetro medio | superficie media | suavidad media | compacidad media | concavidad media | puntos cóncavos medios | simetría media | dimensión fractal media | ... | peor textura | peor perímetro | peor zona | peor suavidad | peor compacidad | peor concavidad | peores puntos cóncavos | peor simetría | peor dimensión fractal | etiqueta | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 564 | 21.56 | 22.39 | 142.00 | 1479.0 | 0.11100 | 0.11590 | 0.24390 | 0.13890 | 0.1726 | 0.05623 | ... | 26.40 | 166.10 | 2027.0 | 0.14100 | 0.21130 | 0.4107 | 0.2216 | 0.2060 | 0.07115 | Benigno |
| 565 | 20.13 | 28.25 | 131.20 | 1261.0 | 0.09780 | 0.10340 | 0.14400 | 0.09791 | 0.1752 | 0.05533 | ... | 38.25 | 155.00 | 1731.0 | 0.11660 | 0.19220 | 0.3215 | 0.1628 | 0.2572 | 0.06637 | Benigno |
| 566 | 16.60 | 28.08 | 108.30 | 858.1 | 0.08455 | 0.10230 | 0.09251 | 0.05302 | 0.1590 | 0.05648 | ... | 34.12 | 126.70 | 1124.0 | 0.11390 | 0.30940 | 0.3403 | 0.1418 | 0.2218 | 0.07820 | Benigno |
| 567 | 20.60 | 29.33 | 140.10 | 1265.0 | 0.11780 | 0.27700 | 0.35140 | 0.15200 | 0.2397 | 0.07016 | ... | 39.42 | 184.60 | 1821.0 | 0.16500 | 0.86810 | 0.9387 | 0.2650 | 0.4087 | 0.12400 | Benigno |
| 568 | 7.76 | 24.54 | 47.92 | 181.0 | 0.05263 | 0.04362 | 0.00000 | 0.00000 | 0.1587 | 0.05884 | ... | 30.37 | 59.16 | 268.6 | 0.08996 | 0.06444 | 0.0000 | 0.0000 | 0.2871 | 0.07039 | Maligno |
5 filas × 31 columnas
CIFAR - 10 Exploración de datos
A continuación, explorarás la CIFAR - 10 conjunto de datos de imágenes
Puedes cargar el CIFAR - 10 utilizando una biblioteca de aprendizaje profundo llamada Keras.
from keras.datasets import cifar10
Una vez importado, utilizarás la función .load_data() para descargar los datos, descargará y almacenará los datos en tu Keras directory. Esto puede llevar algún tiempo en función de tu velocidad de Internet.
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
La línea de código anterior devuelve las imágenes de entrenamiento y de prueba junto con las etiquetas.
Imprimamos rápidamente la forma de las imágenes de entrenamiento y de prueba.
print('Traning data shape:', x_train.shape)
print('Testing data shape:', x_test.shape)
Traning data shape: (50000, 32, 32, 3)
Testing data shape: (10000, 32, 32, 3)
Imprimamos también la forma de las etiquetas.
y_train.shape,y_test.shape
((50000, 1), (10000, 1))
Averigüemos también el número total de etiquetas y los distintos tipos de clases que tienen los datos.
# Find the unique numbers from the train labels
classes = np.unique(y_train)
nClasses = len(classes)
print('Total number of outputs : ', nClasses)
print('Output classes : ', classes)
Total number of outputs : 10
Output classes : [0 1 2 3 4 5 6 7 8 9]
Ahora, para trazar la CIFAR-10 imágenes, importarás matplotlib y utiliza también un magic (%) comando %matplotlib inline ¡para indicar al cuaderno jupyter que muestre la salida dentro del propio cuaderno!
import matplotlib.pyplot as plt
%matplotlib inline
Para entenderlo mejor, vamos a crear un diccionario que tendrá nombres de clase con sus correspondientes etiquetas de clase categóricas.
label_dict = {
0: 'airplane',
1: 'automobile',
2: 'bird',
3: 'cat',
4: 'deer',
5: 'dog',
6: 'frog',
7: 'horse',
8: 'ship',
9: 'truck',
}
plt.figure(figsize=[5,5])
# Display the first image in training data
plt.subplot(121)
curr_img = np.reshape(x_train[0], (32,32,3))
plt.imshow(curr_img)
print(plt.title("(Label: " + str(label_dict[y_train[0][0]]) + ")"))
# Display the first image in testing data
plt.subplot(122)
curr_img = np.reshape(x_test[0],(32,32,3))
plt.imshow(curr_img)
print(plt.title("(Label: " + str(label_dict[y_test[0][0]]) + ")"))
Text(0.5, 1.0, '(Label: frog)')
Text(0.5, 1.0, '(Label: cat)')

Aunque las dos imágenes anteriores están borrosas, de alguna manera puedes observar que la primera imagen es una rana con la etiqueta frogmientras que la segunda imagen es de un gato con la etiqueta cat.
Visualización de datos mediante PCA
Ahora viene la parte más emocionante de este tutorial. Como antes aprendiste que los proyectos PCA convierten datos de alta dimensión en un componente principal de baja dimensión, ¡ahora es el momento de visualizarlo con ayuda de Python!
Visualizar los datos del cáncer de mama
-
Empieza por
Standardizinglos datos, ya que el resultado del ACP se ve influido por la escala de las características de los datos.Es una práctica habitual normalizar los datos antes de alimentar cualquier algoritmo de machine learning.
Para aplicar la normalización, importarás
StandardScalerde la biblioteca sklearn y selecciona sólo las características del módulobreast_datasetque creaste en el paso Exploración de datos. Una vez que tengas las características, aplicarás el escalado haciendofit_transformsobre los datos de las características.Al aplicar StandardScaler, cada característica de tus datos debe tener una distribución normal, de modo que escale la distribución a una media de cero y una desviación típica de uno.
from sklearn.preprocessing import StandardScaler
x = breast_dataset.loc[:, features].values
x = StandardScaler().fit_transform(x) # normalizing the features
x.shape
(569, 30)
Comprobemos si los datos normalizados tienen una media de cero y una desviación típica de uno.
np.mean(x),np.std(x)
(-6.826538293184326e-17, 1.0)
Convirtamos las características normalizadas en un formato tabular con la ayuda de DataFrame.
feat_cols = ['feature'+str(i) for i in range(x.shape[1])]
normalised_breast = pd.DataFrame(x,columns=feat_cols)
normalised_breast.tail()
| feature0 | característica1 | feature2 | feature3 | feature4 | feature5 | feature6 | feature7 | feature8 | feature9 | ... | feature20 | feature21 | feature22 | feature23 | feature24 | feature25 | feature26 | feature27 | feature28 | feature29 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 564 | 2.110995 | 0.721473 | 2.060786 | 2.343856 | 1.041842 | 0.219060 | 1.947285 | 2.320965 | -0.312589 | -0.931027 | ... | 1.901185 | 0.117700 | 1.752563 | 2.015301 | 0.378365 | -0.273318 | 0.664512 | 1.629151 | -1.360158 | -0.709091 |
| 565 | 1.704854 | 2.085134 | 1.615931 | 1.723842 | 0.102458 | -0.017833 | 0.693043 | 1.263669 | -0.217664 | -1.058611 | ... | 1.536720 | 2.047399 | 1.421940 | 1.494959 | -0.691230 | -0.394820 | 0.236573 | 0.733827 | -0.531855 | -0.973978 |
| 566 | 0.702284 | 2.045574 | 0.672676 | 0.577953 | -0.840484 | -0.038680 | 0.046588 | 0.105777 | -0.809117 | -0.895587 | ... | 0.561361 | 1.374854 | 0.579001 | 0.427906 | -0.809587 | 0.350735 | 0.326767 | 0.414069 | -1.104549 | -0.318409 |
| 567 | 1.838341 | 2.336457 | 1.982524 | 1.735218 | 1.525767 | 3.272144 | 3.296944 | 2.658866 | 2.137194 | 1.043695 | ... | 1.961239 | 2.237926 | 2.303601 | 1.653171 | 1.430427 | 3.904848 | 3.197605 | 2.289985 | 1.919083 | 2.219635 |
| 568 | -1.808401 | 1.221792 | -1.814389 | -1.347789 | -3.112085 | -1.150752 | -1.114873 | -1.261820 | -0.820070 | -0.561032 | ... | -1.410893 | 0.764190 | -1.432735 | -1.075813 | -1.859019 | -1.207552 | -1.305831 | -1.745063 | -0.048138 | -0.751207 |
5 filas × 30 columnas
-
Ahora viene la parte crítica, las siguientes líneas de código proyectarán los datos de Cáncer de Mama de treinta dimensiones a dos dimensiones
principal components.Utilizarás la biblioteca sklearn para importar el archivo
PCAy, en el método PCA, pasarás el número de componentes (n_componentes=2) y, por último, llamarás a fit_transform sobre los datos agregados. Aquí, varios componentes representan la dimensión inferior en la que proyectarás tus datos de dimensión superior.
from sklearn.decomposition import PCA
pca_breast = PCA(n_components=2)
principalComponents_breast = pca_breast.fit_transform(x)
A continuación, vamos a crear un DataFrame que tendrá los valores de los componentes principales de las 569 muestras.
principal_breast_Df = pd.DataFrame(data = principalComponents_breast
, columns = ['principal component 1', 'principal component 2'])
principal_breast_Df.tail()
| componente principal 1 | componente principal 2 | |
|---|---|---|
| 564 | 6.439315 | -3.576817 |
| 565 | 3.793382 | -3.584048 |
| 566 | 1.256179 | -1.902297 |
| 567 | 10.374794 | 1.672010 |
| 568 | -5.475243 | -0.670637 |
- Una vez que tengas los componentes principales, puedes encontrar los
explained_variance_ratio. Te proporcionará la cantidad de información o varianza que contiene cada componente principal tras proyectar los datos a un subespacio de menor dimensión.
print('Explained variation per principal component: {}'.format(pca_breast.explained_variance_ratio_))
Explained variation per principal component: [0.44272026 0.18971182]
En la salida anterior, puedes observar que la función principal component 1 contiene el 44,2% de la información, mientras que el principal component 2 sólo contiene el 19% de la información. Además, otro punto a destacar es que al proyectar datos tridimensionales a bidimensionales, se perdió un 36,8% de información.
Vamos a trazar la visualización de las 569 muestras a lo largo del principal component - 1 y principal component - 2 eje. Debería darte una buena idea de cómo se distribuyen tus muestras entre las dos clases.
plt.figure()
plt.figure(figsize=(10,10))
plt.xticks(fontsize=12)
plt.yticks(fontsize=14)
plt.xlabel('Principal Component - 1',fontsize=20)
plt.ylabel('Principal Component - 2',fontsize=20)
plt.title("Principal Component Analysis of Breast Cancer Dataset",fontsize=20)
targets = ['Benign', 'Malignant']
colors = ['r', 'g']
for target, color in zip(targets,colors):
indicesToKeep = breast_dataset['label'] == target
plt.scatter(principal_breast_Df.loc[indicesToKeep, 'principal component 1']
, principal_breast_Df.loc[indicesToKeep, 'principal component 2'], c = color, s = 50)
plt.legend(targets,prop={'size': 15})
<matplotlib.legend.Legend at 0x14552a630>
<Figure size 432x288 with 0 Axes>
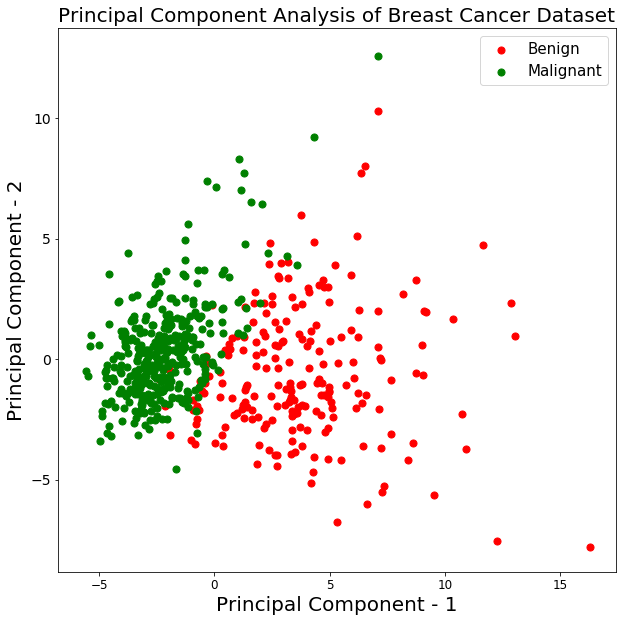
En el gráfico anterior, puedes observar que las dos clases benign y malignantcuando se proyectan a un espacio bidimensional, pueden ser linealmente separables hasta cierto punto. Otras observaciones pueden ser que la benign se extiende en comparación con la clase malignant clase.
Visualización de los datos CIFAR - 10
Las siguientes líneas de código para visualizar los datos de CIFAR-10 son bastante similares a la visualización PCA de los datos del Cáncer de Mama.
- Comprobemos rápidamente los valores máximo y mínimo de las imágenes de entrenamiento CIFAR-10 y
normalizelos píxeles entre 0 y 1, ambos inclusive.
np.min(x_train),np.max(x_train)
(0.0, 1.0)
x_train = x_train/255.0
np.min(x_train),np.max(x_train)
(0.0, 0.00392156862745098)
x_train.shape
(50000, 32, 32, 3)
A continuación, crearás un DataFrame que contendrá los valores en píxeles de las imágenes junto con sus respectivas etiquetas en un formato fila-columna.
Pero antes de eso, vamos a remodelar las dimensiones de la imagen de tres a una (aplanar las imágenes).
x_train_flat = x_train.reshape(-1,3072)
feat_cols = ['pixel'+str(i) for i in range(x_train_flat.shape[1])]
df_cifar = pd.DataFrame(x_train_flat,columns=feat_cols)
df_cifar['label'] = y_train
print('Size of the dataframe: {}'.format(df_cifar.shape))
Size of the dataframe: (50000, 3073)
Perfecto. El tamaño del marco de datos es correcto, ya que hay 50.000 imágenes de entrenamiento, cada una de las cuales tiene 3072 píxeles y una columna adicional para las etiquetas, por lo que en total hay 3073.
El ACP se aplicará en todas las columnas excepto en la última, que es la etiqueta de cada imagen.
df_cifar.head()
| pixel0 | pixel1 | pixel2 | pixel3 | pixel4 | pixel5 | pixel6 | pixel7 | pixel8 | pixel9 | ... | pixel3063 | pixel3064 | pixel3065 | pixel3066 | pixel3067 | pixel3068 | pixel3069 | pixel3070 | pixel3071 | etiqueta | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.231373 | 0.243137 | 0.247059 | 0.168627 | 0.180392 | 0.176471 | 0.196078 | 0.188235 | 0.168627 | 0.266667 | ... | 0.847059 | 0.721569 | 0.549020 | 0.592157 | 0.462745 | 0.329412 | 0.482353 | 0.360784 | 0.282353 | 6 |
| 1 | 0.603922 | 0.694118 | 0.733333 | 0.494118 | 0.537255 | 0.533333 | 0.411765 | 0.407843 | 0.372549 | 0.400000 | ... | 0.560784 | 0.521569 | 0.545098 | 0.560784 | 0.525490 | 0.556863 | 0.560784 | 0.521569 | 0.564706 | 9 |
| 2 | 1.000000 | 1.000000 | 1.000000 | 0.992157 | 0.992157 | 0.992157 | 0.992157 | 0.992157 | 0.992157 | 0.992157 | ... | 0.305882 | 0.333333 | 0.325490 | 0.309804 | 0.333333 | 0.325490 | 0.313725 | 0.337255 | 0.329412 | 9 |
| 3 | 0.109804 | 0.098039 | 0.039216 | 0.145098 | 0.133333 | 0.074510 | 0.149020 | 0.137255 | 0.078431 | 0.164706 | ... | 0.211765 | 0.184314 | 0.109804 | 0.247059 | 0.219608 | 0.145098 | 0.282353 | 0.254902 | 0.180392 | 4 |
| 4 | 0.666667 | 0.705882 | 0.776471 | 0.658824 | 0.698039 | 0.768627 | 0.694118 | 0.725490 | 0.796078 | 0.717647 | ... | 0.294118 | 0.309804 | 0.321569 | 0.278431 | 0.294118 | 0.305882 | 0.286275 | 0.301961 | 0.313725 | 1 |
5 filas × 3073 columnas
- A continuación, crearás el método PCA, pasarás el número de componentes a dos y aplicarás
fit_transformen los datos de entrenamiento, esto puede tardar unos segundos ya que hay 50.000 muestras
pca_cifar = PCA(n_components=2)
principalComponents_cifar = pca_cifar.fit_transform(df_cifar.iloc[:,:-1])
A continuación, convertirás los componentes principales de cada una de las 50.000 imágenes de una matriz numpy a un DataFrame pandas.
principal_cifar_Df = pd.DataFrame(data = principalComponents_cifar
, columns = ['principal component 1', 'principal component 2'])
principal_cifar_Df['y'] = y_train
principal_cifar_Df.head()
| componente principal 1 | componente principal 2 | y | |
|---|---|---|---|
| 0 | -6.401018 | 2.729039 | 6 |
| 1 | 0.829783 | -0.949943 | 9 |
| 2 | 7.730200 | -11.522102 | 9 |
| 3 | -10.347817 | 0.010738 | 4 |
| 4 | -2.625651 | -4.969240 | 1 |
- Averigüemos rápidamente la cantidad de información o
variancese mantienen los componentes principales.
print('Explained variation per principal component: {}'.format(pca_cifar.explained_variance_ratio_))
Explained variation per principal component: [0.2907663 0.11253144]
Bueno, parece que los componentes principales 1 y 2 retuvieron una cantidad decente de información, dado que los datos se proyectaron de 3072 dimensiones a sólo dos componentes principales.
Ha llegado el momento de visualizar los datos CIFAR-10 en un espacio bidimensional. Recuerda que hay cierto solapamiento de clases semánticas en este conjunto de datos, lo que significa que una rana puede tener una forma ligeramente similar a la de un gato o un ciervo a la de un perro; sobre todo cuando se proyecta en un espacio bidimensional. Puede que las diferencias entre ellos no se capten tan bien.
import seaborn as sns
plt.figure(figsize=(16,10))
sns.scatterplot(
x="principal component 1", y="principal component 2",
hue="y",
palette=sns.color_palette("hls", 10),
data=principal_cifar_Df,
legend="full",
alpha=0.3
)
<matplotlib.axes._subplots.AxesSubplot at 0x12a5ba8d0>
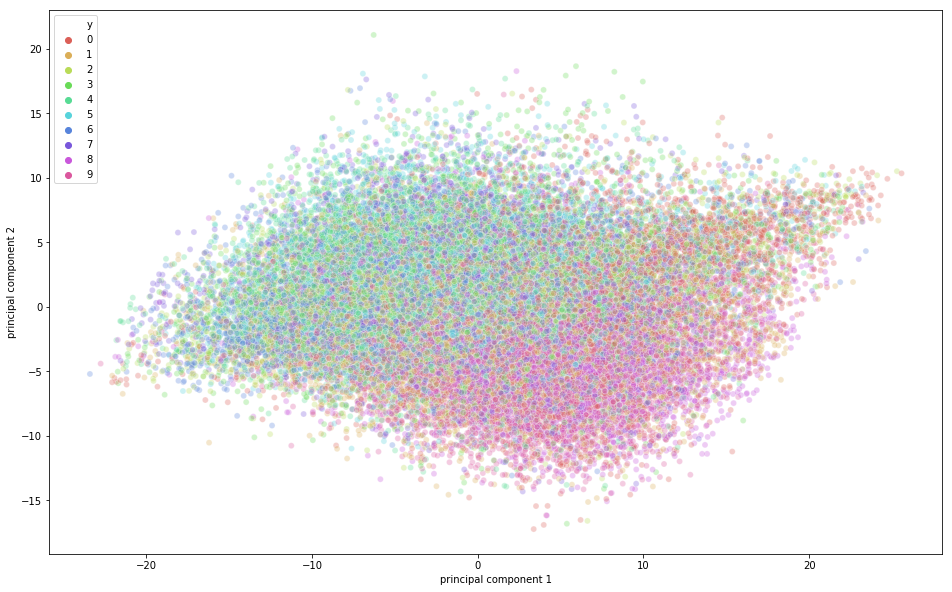
En la figura anterior, puedes observar que los componentes principales captaron cierta variación, ya que hay cierta estructura en los puntos cuando se proyectan a lo largo de los dos ejes de componentes principales. Los puntos que pertenecen a la misma clase están cerca unos de otros, y los puntos o imágenes que son muy diferentes semánticamente están más alejados unos de otros.
Acelera el entrenamiento del aprendizaje profundo utilizando PCA con el conjunto de datos CIFAR - 10
En este segmento final del tutorial, aprenderás cómo puedes acelerar el proceso de entrenamiento de tu modelo de Aprendizaje Profundo utilizando PCA.
Nota: Para aprender las terminologías básicas que se utilizarán en esta sección, no dudes en consultar este tutorial.
En primer lugar, normalicemos las imágenes de entrenamiento y de prueba. Si recuerdas, las imágenes de entrenamiento se normalizaron en la parte de visualización del ACP, así que sólo tienes que normalizar las imágenes de prueba. Así que, ¡hagámoslo rápidamente!
x_test = x_test/255.0
x_test = x_test.reshape(-1,32,32,3)
Vamos a reshape los datos de la prueba.
x_test_flat = x_test.reshape(-1,3072)
A continuación, realizarás la instancia del modelo PCA.
Aquí también puedes pasar cuánta varianza quieres que capte el ACP. Pasemos 0,9 como parámetro al modelo PCA, lo que significa que el PCA retendrá el 90% de la varianza y el number of components necesario para captar el 90% de variación.
Ten en cuenta que antes pasaste n_components como parámetro y así podrías averiguar cuánta varianza captan esos dos componentes. Pero aquí mencionamos explícitamente cuánta varianza queremos que capte el ACP y, por tanto, la n_components variará en función del parámetro de varianza.
Si no pasas ninguna varianza, el número de componentes será igual a la dimensión original de los datos.
pca = PCA(0.9)
Entonces encajarás el PCA sobre las imágenes de entrenamiento.
pca.fit(x_train_flat)
PCA(copy=True, iterated_power='auto', n_components=0.9, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
Ahora vamos a averiguar cuántos n_components Se utilizó el ACP para captar el 0,9 de varianza.
pca.n_components_
99
En la salida anterior, puedes observar que para conseguir una varianza del 90%, la dimensión se redujo a 99 componentes principales de la 3072 dimensiones.
Por último, aplicarás transform tanto en el conjunto de entrenamiento como en el de prueba para generar un conjunto de datos transformado a partir de los parámetros generados por el fit .
train_img_pca = pca.transform(x_train_flat)
test_img_pca = pca.transform(x_test_flat)
A continuación, vamos a importar rápidamente las bibliotecas necesarias para ejecutar el modelo de aprendizaje profundo.
from keras.models import Sequential
from keras.layers import Dense
from keras.utils import np_utils
from keras.optimizers import RMSprop
Ahora, convertirás tus etiquetas de entrenamiento y prueba en vectores de codificación de un solo golpe.
y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
Vamos a definir el número de épocas, el número de clases y el tamaño del lote para tu modelo.
batch_size = 128
num_classes = 10
epochs = 20
A continuación, definirás tu Sequential ¡modelo!
model = Sequential()
model.add(Dense(1024, activation='relu', input_shape=(99,)))
model.add(Dense(1024, activation='relu'))
model.add(Dense(512, activation='relu'))
model.add(Dense(256, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
Imprimamos el resumen del modelo.
model.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 1024) 102400
_________________________________________________________________
dense_2 (Dense) (None, 1024) 1049600
_________________________________________________________________
dense_3 (Dense) (None, 512) 524800
_________________________________________________________________
dense_4 (Dense) (None, 256) 131328
_________________________________________________________________
dense_5 (Dense) (None, 10) 2570
=================================================================
Total params: 1,810,698
Trainable params: 1,810,698
Non-trainable params: 0
_________________________________________________________________
Por último, ¡es hora de compilar y entrenar el modelo!
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
history = model.fit(train_img_pca, y_train,batch_size=batch_size,epochs=epochs,verbose=1,
validation_data=(test_img_pca, y_test))
WARNING:tensorflow:From /Users/adityasharma/blog/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:2704: calling reduce_sum (from tensorflow.python.ops.math_ops) with keep_dims is deprecated and will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead
WARNING:tensorflow:From /Users/adityasharma/blog/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:1257: calling reduce_mean (from tensorflow.python.ops.math_ops) with keep_dims is deprecated and will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead
Train on 50000 samples, validate on 10000 samples
Epoch 1/20
50000/50000 [==============================] - 7s - loss: 1.9032 - acc: 0.2962 - val_loss: 1.6925 - val_acc: 0.3875
Epoch 2/20
50000/50000 [==============================] - 7s - loss: 1.6480 - acc: 0.4055 - val_loss: 1.5313 - val_acc: 0.4412
Epoch 3/20
50000/50000 [==============================] - 7s - loss: 1.5205 - acc: 0.4534 - val_loss: 1.4609 - val_acc: 0.4695
Epoch 4/20
50000/50000 [==============================] - 7s - loss: 1.4322 - acc: 0.4849 - val_loss: 1.6164 - val_acc: 0.4503
Epoch 5/20
50000/50000 [==============================] - 7s - loss: 1.3621 - acc: 0.5120 - val_loss: 1.3626 - val_acc: 0.5081
Epoch 6/20
50000/50000 [==============================] - 7s - loss: 1.2995 - acc: 0.5330 - val_loss: 1.4100 - val_acc: 0.4940
Epoch 7/20
50000/50000 [==============================] - 7s - loss: 1.2473 - acc: 0.5529 - val_loss: 1.3589 - val_acc: 0.5251
Epoch 8/20
50000/50000 [==============================] - 7s - loss: 1.2010 - acc: 0.5669 - val_loss: 1.3315 - val_acc: 0.5232
Epoch 9/20
50000/50000 [==============================] - 7s - loss: 1.1524 - acc: 0.5868 - val_loss: 1.3903 - val_acc: 0.5197
Epoch 10/20
50000/50000 [==============================] - 7s - loss: 1.1134 - acc: 0.6013 - val_loss: 1.2722 - val_acc: 0.5499
Epoch 11/20
50000/50000 [==============================] - 7s - loss: 1.0691 - acc: 0.6160 - val_loss: 1.5911 - val_acc: 0.4768
Epoch 12/20
50000/50000 [==============================] - 7s - loss: 1.0325 - acc: 0.6289 - val_loss: 1.2515 - val_acc: 0.5602
Epoch 13/20
50000/50000 [==============================] - 7s - loss: 0.9977 - acc: 0.6420 - val_loss: 1.5678 - val_acc: 0.4914
Epoch 14/20
50000/50000 [==============================] - 8s - loss: 0.9567 - acc: 0.6567 - val_loss: 1.3525 - val_acc: 0.5418
Epoch 15/20
50000/50000 [==============================] - 9s - loss: 0.9158 - acc: 0.6713 - val_loss: 1.3525 - val_acc: 0.5540
Epoch 16/20
50000/50000 [==============================] - 10s - loss: 0.8948 - acc: 0.6816 - val_loss: 1.5633 - val_acc: 0.5156
Epoch 17/20
50000/50000 [==============================] - 9s - loss: 0.8690 - acc: 0.6903 - val_loss: 1.6980 - val_acc: 0.5084
Epoch 18/20
50000/50000 [==============================] - 9s - loss: 0.8586 - acc: 0.7002 - val_loss: 1.6325 - val_acc: 0.5247
Epoch 19/20
50000/50000 [==============================] - 8s - loss: 0.9367 - acc: 0.6853 - val_loss: 1.8253 - val_acc: 0.5165
Epoch 20/20
50000/50000 [==============================] - 8s - loss: 2.3761 - acc: 0.5971 - val_loss: 6.0192 - val_acc: 0.4409
A partir del resultado anterior, puedes observar que el tiempo empleado en entrenar cada época fue de sólo 7 seconds en una CPU. El modelo hizo un trabajo decente con los datos de entrenamiento, consiguiendo 70% precisión, mientras que sólo consiguió 56% precisión en la prueba dat. Esto significa que sobreajustó los datos de entrenamiento. Sin embargo, recuerda que los datos se proyectaron a 99 dimensiones de 3072 dimensiones y, a pesar de ello, ¡hizo un gran trabajo!
Por último, veamos cuánto tiempo tarda el modelo en entrenarse en el conjunto de datos original y cuánta precisión puede conseguir utilizando el mismo modelo de aprendizaje profundo.
model = Sequential()
model.add(Dense(1024, activation='relu', input_shape=(3072,)))
model.add(Dense(1024, activation='relu'))
model.add(Dense(512, activation='relu'))
model.add(Dense(256, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
history = model.fit(x_train_flat, y_train,batch_size=batch_size,epochs=epochs,verbose=1,
validation_data=(x_test_flat, y_test))
Train on 50000 samples, validate on 10000 samples
Epoch 1/20
50000/50000 [==============================] - 23s - loss: 2.0657 - acc: 0.2200 - val_loss: 2.0277 - val_acc: 0.2485
Epoch 2/20
50000/50000 [==============================] - 22s - loss: 1.8727 - acc: 0.3166 - val_loss: 1.8428 - val_acc: 0.3215
Epoch 3/20
50000/50000 [==============================] - 22s - loss: 1.7801 - acc: 0.3526 - val_loss: 1.7657 - val_acc: 0.3605
Epoch 4/20
50000/50000 [==============================] - 22s - loss: 1.7141 - acc: 0.3796 - val_loss: 1.6345 - val_acc: 0.4132
Epoch 5/20
50000/50000 [==============================] - 22s - loss: 1.6566 - acc: 0.4001 - val_loss: 1.6384 - val_acc: 0.4076
Epoch 6/20
50000/50000 [==============================] - 22s - loss: 1.6083 - acc: 0.4209 - val_loss: 1.7507 - val_acc: 0.3574
Epoch 7/20
50000/50000 [==============================] - 22s - loss: 1.5626 - acc: 0.4374 - val_loss: 1.7125 - val_acc: 0.4010
Epoch 8/20
50000/50000 [==============================] - 22s - loss: 1.5252 - acc: 0.4486 - val_loss: 1.5914 - val_acc: 0.4321
Epoch 9/20
50000/50000 [==============================] - 24s - loss: 1.4924 - acc: 0.4620 - val_loss: 1.5352 - val_acc: 0.4616
Epoch 10/20
50000/50000 [==============================] - 25s - loss: 1.4627 - acc: 0.4728 - val_loss: 1.4561 - val_acc: 0.4798
Epoch 11/20
50000/50000 [==============================] - 24s - loss: 1.4349 - acc: 0.4820 - val_loss: 1.5044 - val_acc: 0.4723
Epoch 12/20
50000/50000 [==============================] - 24s - loss: 1.4120 - acc: 0.4919 - val_loss: 1.4740 - val_acc: 0.4790
Epoch 13/20
50000/50000 [==============================] - 23s - loss: 1.3913 - acc: 0.4981 - val_loss: 1.4430 - val_acc: 0.4891
Epoch 14/20
50000/50000 [==============================] - 27s - loss: 1.3678 - acc: 0.5098 - val_loss: 1.4323 - val_acc: 0.4888
Epoch 15/20
50000/50000 [==============================] - 27s - loss: 1.3508 - acc: 0.5148 - val_loss: 1.6179 - val_acc: 0.4372
Epoch 16/20
50000/50000 [==============================] - 25s - loss: 1.3443 - acc: 0.5167 - val_loss: 1.5868 - val_acc: 0.4656
Epoch 17/20
50000/50000 [==============================] - 25s - loss: 1.3734 - acc: 0.5101 - val_loss: 1.4756 - val_acc: 0.4913
Epoch 18/20
50000/50000 [==============================] - 26s - loss: 5.5126 - acc: 0.3591 - val_loss: 5.7580 - val_acc: 0.3084
Epoch 19/20
50000/50000 [==============================] - 27s - loss: 5.6346 - acc: 0.3395 - val_loss: 3.7362 - val_acc: 0.3402
Epoch 20/20
50000/50000 [==============================] - 26s - loss: 6.4199 - acc: 0.3030 - val_loss: 13.9429 - val_acc: 0.1326
¡Voilà! A partir de los resultados anteriores, es evidente que el tiempo empleado en el entrenamiento de cada época fue de aproximadamente 23 seconds en una CPU que era casi tres veces mayor que el modelo entrenado con el resultado del PCA.
Además, tanto la precisión de entrenamiento como la de prueba son inferiores a la precisión que conseguiste con los 99 componentes principales como entrada al modelo.
Así pues, aplicando el PCA a los datos de entrenamiento pudiste entrenar tu algoritmo de aprendizaje profundo no sólo fastpero también consiguió mejores accuracy en los datos de prueba en comparación con el algoritmo de aprendizaje profundo entrenado con los datos de entrenamiento originales.
¡Ve más lejos!
Enhorabuena por terminar el tutorial.
Este tutorial fue una excelente y completa introducción al ACP en Python, que cubrió tanto los conceptos teóricos como los prácticos del ACP.
Si quieres profundizar en las técnicas de reducción de la dimensionalidad, considera la posibilidad de leer sobre la incrustación estocástica de vecinos distribuida en t, conocida comúnmente como tSNE, que es una técnica probabilística no lineal de reducción de la dimensionalidad.
Si quieres aprender más sobre técnicas de aprendizaje no supervisado como el PCA, sigue el curso Aprendizaje no supervisado en Python de DataCamp.
Referencias:

