Cours
Exécutez et modifiez le code de ce tutoriel en ligne
Exécuter le codeL'analyse en composantes principales (ACP) est une technique de réduction de la dimensionnalité linéaire qui peut être utilisée pour extraire des informations d'un espace de haute dimension en les projetant dans un sous-espace de dimension inférieure. Si vous êtes familier avec le langage de l'algèbre linéaire, vous pourriez également dire que l'analyse en composantes principales consiste à trouver les vecteurs propres de la matrice de covariance afin d'identifier les directions de la variance maximale dans les données.
L'ACP est une technique de réduction de la dimensionnalité non supervisée. Vous pouvez donc regrouper des points de données similaires sur la base de leur corrélation sans aucune supervision (ou étiquette).
Note: Les caractéristiques, les dimensions et les variables font toutes référence à la même chose. Vous les trouverez utilisés de manière interchangeable.
Où pouvez-vous appliquer l'APC ?
-
Visualisation des données: Lorsque vous travaillez sur un problème lié aux données, le défi dans le monde d'aujourd'hui est le volume de données et les variables/caractéristiques qui définissent ces données. Pour résoudre un problème où les données sont essentielles, vous devez procéder à une exploration approfondie des données, par exemple pour déterminer la corrélation entre les variables ou comprendre la distribution de quelques variables. Compte tenu du grand nombre de variables ou de dimensions selon lesquelles les données sont réparties, la visualisation peut s'avérer difficile, voire impossible.
L'ACP peut donc le faire pour vous puisqu'elle projette les données dans une dimension inférieure, ce qui vous permet de visualiser les données dans un espace 2D ou 3D à l'œil nu.
-
Accélérer un algorithme d'apprentissage automatique (ML): L'idée principale de l'ACP étant la réduction de la dimensionnalité, vous pouvez l'exploiter pour accélérer le temps de formation et de test de votre algorithme d'apprentissage automatique si vos données comportent un grand nombre de caractéristiques et que l'apprentissage de l'algorithme d'apprentissage automatique est trop lent.
À un niveau abstrait, vous prenez un ensemble de données comportant de nombreuses caractéristiques et vous simplifiez cet ensemble de données en sélectionnant quelques Principal Components à partir des caractéristiques originales.
Qu'est-ce qu'une composante principale ?
Les composantes principales sont la clé de l'ACP ; elles représentent ce qui se cache sous le capot de vos données. En termes simples, lorsque les données sont projetées dans une dimension inférieure (supposons trois dimensions) à partir d'un espace supérieur, les trois dimensions ne sont rien d'autre que les trois composantes principales qui capturent (ou détiennent) la majeure partie de la variance (information) de vos données.
Les composantes principales ont à la fois une direction et une ampleur. La direction représente les axes principaux sur lesquels les données sont principalement réparties ou présentent le plus de variance, et l'ampleur signifie la quantité de variance que la composante principale capture des données lorsqu'elle est projetée sur cet axe. Les composantes principales forment une ligne droite, et la première composante principale contient la plus grande variance des données. Chaque composante principale suivante est orthogonale à la précédente et a une variance moindre. De cette manière, étant donné un ensemble de x variables corrélées sur y échantillons, vous obtenez un ensemble de u composantes principales non corrélées sur les mêmes y échantillons.
La raison pour laquelle vous obtenez des composantes principales non corrélées à partir des caractéristiques d'origine est que les caractéristiques corrélées contribuent à la même composante principale, réduisant ainsi les caractéristiques des données d'origine en composantes principales non corrélées, chacune représentant un ensemble différent de caractéristiques corrélées avec des degrés de variabilité différents. Chaque composante principale représente un pourcentage de la variabilité totale des données.
Dans le tutoriel d'aujourd'hui, nous appliquerons l'ACP pour obtenir des informations grâce à la visualisation des données, et nous appliquerons également l'ACP pour accélérer notre algorithme d'apprentissage automatique. Pour accomplir les deux tâches susmentionnées, vous utiliserez deux ensembles de données célèbres : Cancer du sein et CIFAR - 10. Le premier est un ensemble de données numériques ; le second est un ensemble de données d'images.
Comprendre les données
Avant de charger les données, il est bon de comprendre et d'examiner les données avec lesquelles vous allez travailler !
Cancer du sein
L'ensemble de données sur le cancer du sein est une donnée multivariée à valeurs réelles qui se compose de deux classes, chaque classe indiquant si une patiente est atteinte ou non d'un cancer du sein. Les deux catégories sont : les tumeurs malignes et les tumeurs bénignes.
La classe maligne compte 212 échantillons, tandis que la classe bénigne en compte 357.
Il comporte 30 caractéristiques communes à toutes les classes : rayon, texture, périmètre, surface, douceur, dimension fractale, etc.
Vous pouvez télécharger l'ensemble de données sur le cancer du sein à partir d'ici ou, plus simplement, le charger à l'aide de la bibliothèque sklearn.
CIFAR - 10
L'ensemble de données CIFAR-10 (Canadian Institute For Advanced Research) se compose de 60000 images de 32x32x3 couleurs réparties en dix classes, avec 6000 images par catégorie.
L'ensemble de données se compose de 50000 images d'apprentissage et de 10000 images de test.
Les classes de l'ensemble de données sont les suivantes : avion, automobile, oiseau, chat, cerf, chien, grenouille, cheval, bateau, camion.
Vous pouvez télécharger le jeu de données CIFAR à partir d'ici, ou vous pouvez également le charger à la volée avec l'aide d'une bibliothèque d'apprentissage profond comme Keras.
Exploration des données à l'aide de l'ACP
Vous allez maintenant charger et analyser les ensembles de données Breast Cancer et CIFAR-10. Vous avez maintenant une idée de la dimensionnalité des deux ensembles de données.
Explorons donc rapidement les deux ensembles de données.
Exploration des données sur le cancer du sein
Commençons par explorer l'ensemble de données Breast Cancer.
Vous utiliserez le module sklearn's datasets et en importerez l'ensemble de données Breast Cancer.
from sklearn.datasets import load_breast_cancer
load_breast_cancer vous donnera les deux étiquettes et les données. Pour récupérer les données, vous appellerez .data et pour récupérer les étiquettes .target.
Les données comportent 569 échantillons avec trente caractéristiques, et chaque échantillon est associé à une étiquette. Cet ensemble de données comporte deux étiquettes.
breast = load_breast_cancer()
breast_data = breast.data
Vérifions la forme des données.
breast_data.shape
(569, 30)
Même si pour ce tutoriel, vous n'avez pas besoin des étiquettes, pour une meilleure compréhension, chargeons les étiquettes et vérifions la forme.
breast_labels = breast.target
breast_labels.shape
(569,)
Vous allez maintenant importer numpy puisque vous allez remodeler breast_labels pour le concaténer avec breast_data afin de créer un DataFrame qui contiendra à la fois les données et les étiquettes.
import numpy as np
labels = np.reshape(breast_labels,(569,1))
Après reshaping les étiquettes, vous allez concatenate les données et les étiquettes le long du deuxième axe, ce qui signifie que la forme finale du tableau sera 569 x 31.
final_breast_data = np.concatenate([breast_data,labels],axis=1)
final_breast_data.shape
(569, 31)
Vous allez maintenant importer pandas pour créer DataFrame des données finales afin de représenter les données sous forme de tableau.
import pandas as pd
breast_dataset = pd.DataFrame(final_breast_data)
Imprimons rapidement les caractéristiques présentes dans l'ensemble de données sur le cancer du sein !
features = breast.feature_names
features
array(['mean radius', 'mean texture', 'mean perimeter', 'mean area',
'mean smoothness', 'mean compactness', 'mean concavity',
'mean concave points', 'mean symmetry', 'mean fractal dimension',
'radius error', 'texture error', 'perimeter error', 'area error',
'smoothness error', 'compactness error', 'concavity error',
'concave points error', 'symmetry error',
'fractal dimension error', 'worst radius', 'worst texture',
'worst perimeter', 'worst area', 'worst smoothness',
'worst compactness', 'worst concavity', 'worst concave points',
'worst symmetry', 'worst fractal dimension'], dtype='<U23')
Si vous notez dans le tableau features, le champ label est manquant. Par conséquent, vous devrez l'ajouter manuellement au tableau features puisque vous assimilerez ce tableau aux noms des colonnes de votre DataFrame breast_dataset.
features_labels = np.append(features,'label')
C'est très bien ! Vous allez maintenant intégrer les noms des colonnes dans le DataFrame breast_dataset.
breast_dataset.columns = features_labels
Imprimons les premières lignes du DataFrame.
breast_dataset.head()
| rayon moyen | texture moyenne | périmètre moyen | surface moyenne | Lissage moyen | compacité moyenne | concavité moyenne | points concaves moyens | symétrie moyenne | dimension fractale moyenne | ... | la plus mauvaise texture | le plus mauvais périmètre | pire zone | la pire des lissages | la pire compacité | pire concavité | les points les plus concaves | la pire symétrie | la pire dimension fractale | étiquette | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 17.99 | 10.38 | 122.80 | 1001.0 | 0.11840 | 0.27760 | 0.3001 | 0.14710 | 0.2419 | 0.07871 | ... | 17.33 | 184.60 | 2019.0 | 0.1622 | 0.6656 | 0.7119 | 0.2654 | 0.4601 | 0.11890 | 0.0 |
| 1 | 20.57 | 17.77 | 132.90 | 1326.0 | 0.08474 | 0.07864 | 0.0869 | 0.07017 | 0.1812 | 0.05667 | ... | 23.41 | 158.80 | 1956.0 | 0.1238 | 0.1866 | 0.2416 | 0.1860 | 0.2750 | 0.08902 | 0.0 |
| 2 | 19.69 | 21.25 | 130.00 | 1203.0 | 0.10960 | 0.15990 | 0.1974 | 0.12790 | 0.2069 | 0.05999 | ... | 25.53 | 152.50 | 1709.0 | 0.1444 | 0.4245 | 0.4504 | 0.2430 | 0.3613 | 0.08758 | 0.0 |
| 3 | 11.42 | 20.38 | 77.58 | 386.1 | 0.14250 | 0.28390 | 0.2414 | 0.10520 | 0.2597 | 0.09744 | ... | 26.50 | 98.87 | 567.7 | 0.2098 | 0.8663 | 0.6869 | 0.2575 | 0.6638 | 0.17300 | 0.0 |
| 4 | 20.29 | 14.34 | 135.10 | 1297.0 | 0.10030 | 0.13280 | 0.1980 | 0.10430 | 0.1809 | 0.05883 | ... | 16.67 | 152.20 | 1575.0 | 0.1374 | 0.2050 | 0.4000 | 0.1625 | 0.2364 | 0.07678 | 0.0 |
5 lignes × 31 colonnes
Les étiquettes d'origine étant au format 0,1, vous les changerez en benign et malignant à l'aide de la fonction .replace. Vous utiliserez inplace=True qui modifiera le DataFrame breast_dataset.
breast_dataset['label'].replace(0, 'Benign',inplace=True)
breast_dataset['label'].replace(1, 'Malignant',inplace=True)
Imprimons les dernières lignes du site breast_dataset.
breast_dataset.tail()
| rayon moyen | texture moyenne | périmètre moyen | surface moyenne | Lissage moyen | compacité moyenne | concavité moyenne | points concaves moyens | symétrie moyenne | dimension fractale moyenne | ... | la plus mauvaise texture | le plus mauvais périmètre | pire zone | la pire des lissages | la pire compacité | pire concavité | les points les plus concaves | la pire symétrie | la pire dimension fractale | étiquette | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 564 | 21.56 | 22.39 | 142.00 | 1479.0 | 0.11100 | 0.11590 | 0.24390 | 0.13890 | 0.1726 | 0.05623 | ... | 26.40 | 166.10 | 2027.0 | 0.14100 | 0.21130 | 0.4107 | 0.2216 | 0.2060 | 0.07115 | Bénigne |
| 565 | 20.13 | 28.25 | 131.20 | 1261.0 | 0.09780 | 0.10340 | 0.14400 | 0.09791 | 0.1752 | 0.05533 | ... | 38.25 | 155.00 | 1731.0 | 0.11660 | 0.19220 | 0.3215 | 0.1628 | 0.2572 | 0.06637 | Bénigne |
| 566 | 16.60 | 28.08 | 108.30 | 858.1 | 0.08455 | 0.10230 | 0.09251 | 0.05302 | 0.1590 | 0.05648 | ... | 34.12 | 126.70 | 1124.0 | 0.11390 | 0.30940 | 0.3403 | 0.1418 | 0.2218 | 0.07820 | Bénigne |
| 567 | 20.60 | 29.33 | 140.10 | 1265.0 | 0.11780 | 0.27700 | 0.35140 | 0.15200 | 0.2397 | 0.07016 | ... | 39.42 | 184.60 | 1821.0 | 0.16500 | 0.86810 | 0.9387 | 0.2650 | 0.4087 | 0.12400 | Bénigne |
| 568 | 7.76 | 24.54 | 47.92 | 181.0 | 0.05263 | 0.04362 | 0.00000 | 0.00000 | 0.1587 | 0.05884 | ... | 30.37 | 59.16 | 268.6 | 0.08996 | 0.06444 | 0.0000 | 0.0000 | 0.2871 | 0.07039 | Malignant |
5 lignes × 31 colonnes
CIFAR - 10 explorations de données
Ensuite, vous explorerez l'ensemble de données d'images CIFAR - 10.
Vous pouvez charger l'ensemble de données CIFAR - 10 à l'aide d'une bibliothèque d'apprentissage profond appelée Keras.
from keras.datasets import cifar10
Une fois les données importées, vous utiliserez la méthode .load_data() pour les télécharger et les stocker dans votre répertoire Keras. Cette opération peut prendre un certain temps en fonction de votre vitesse Internet.
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
La ligne de code ci-dessus renvoie les images d'apprentissage et de test avec les étiquettes.
Imprimons rapidement la forme des images d'entraînement et de test.
print('Traning data shape:', x_train.shape)
print('Testing data shape:', x_test.shape)
Traning data shape: (50000, 32, 32, 3)
Testing data shape: (10000, 32, 32, 3)
Imprimons également la forme des étiquettes.
y_train.shape,y_test.shape
((50000, 1), (10000, 1))
Déterminons également le nombre total d'étiquettes et les différents types de classes que comportent les données.
# Find the unique numbers from the train labels
classes = np.unique(y_train)
nClasses = len(classes)
print('Total number of outputs : ', nClasses)
print('Output classes : ', classes)
Total number of outputs : 10
Output classes : [0 1 2 3 4 5 6 7 8 9]
Maintenant, pour tracer les images CIFAR-10, vous allez importer matplotlib et également utiliser une commande magic (%) %matplotlib inline pour dire au notebook jupyter d'afficher la sortie à l'intérieur du notebook lui-même !
import matplotlib.pyplot as plt
%matplotlib inline
Pour une meilleure compréhension, créons un dictionnaire qui contiendra les noms des classes avec leurs étiquettes catégorielles correspondantes.
label_dict = {
0: 'airplane',
1: 'automobile',
2: 'bird',
3: 'cat',
4: 'deer',
5: 'dog',
6: 'frog',
7: 'horse',
8: 'ship',
9: 'truck',
}
plt.figure(figsize=[5,5])
# Display the first image in training data
plt.subplot(121)
curr_img = np.reshape(x_train[0], (32,32,3))
plt.imshow(curr_img)
print(plt.title("(Label: " + str(label_dict[y_train[0][0]]) + ")"))
# Display the first image in testing data
plt.subplot(122)
curr_img = np.reshape(x_test[0],(32,32,3))
plt.imshow(curr_img)
print(plt.title("(Label: " + str(label_dict[y_test[0][0]]) + ")"))
Text(0.5, 1.0, '(Label: frog)')
Text(0.5, 1.0, '(Label: cat)')

Même si les deux images ci-dessus sont floues, vous pouvez toujours observer que la première image est une grenouille portant l'étiquette frog, tandis que la seconde image est celle d'un chat portant l'étiquette cat.
Visualisation des données à l'aide de l'ACP
Voici maintenant la partie la plus excitante de ce tutoriel. Comme vous avez appris plus tôt que les projets d'ACP transforment des données de haute dimension en une composante principale de faible dimension, il est maintenant temps de visualiser cela avec l'aide de Python!
Visualiser les données sur le cancer du sein
-
Vous commencez par
Standardizingles données, car les résultats de l'ACP sont influencés par l'échelle des caractéristiques des données.Il est courant de normaliser vos données avant de les introduire dans un algorithme d'apprentissage automatique.
Pour appliquer la normalisation, vous allez importer le module
StandardScalerde la bibliothèque sklearn et sélectionner uniquement les caractéristiques du sitebreast_datasetque vous avez créé à l'étape Exploration des données. Une fois que vous avez les caractéristiques, vous appliquerez la mise à l'échelle en faisantfit_transformsur les données des caractéristiques.Lors de l'application de StandardScaler, chaque caractéristique de vos données doit être normalement distribuée de manière à ce que la distribution soit mise à l'échelle avec une moyenne de zéro et un écart-type de un.
from sklearn.preprocessing import StandardScaler
x = breast_dataset.loc[:, features].values
x = StandardScaler().fit_transform(x) # normalizing the features
x.shape
(569, 30)
Vérifions si les données normalisées ont une moyenne de zéro et un écart-type de un.
np.mean(x),np.std(x)
(-6.826538293184326e-17, 1.0)
Convertissons les caractéristiques normalisées en un format tabulaire à l'aide de DataFrame.
feat_cols = ['feature'+str(i) for i in range(x.shape[1])]
normalised_breast = pd.DataFrame(x,columns=feat_cols)
normalised_breast.tail()
| caractéristique0 | caractéristique1 | fonctionnalité2 | caractéristique3 | caractéristique4 | caractéristique5 | caractéristique6 | fonctionnalité7 | caractéristique8 | caractéristique9 | ... | caractéristique20 | fonctionnalité21 | caractéristique22 | caractéristique23 | fonctionnalité24 | caractéristique25 | caractéristique26 | caractéristique27 | caractéristique28 | caractéristique29 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 564 | 2.110995 | 0.721473 | 2.060786 | 2.343856 | 1.041842 | 0.219060 | 1.947285 | 2.320965 | -0.312589 | -0.931027 | ... | 1.901185 | 0.117700 | 1.752563 | 2.015301 | 0.378365 | -0.273318 | 0.664512 | 1.629151 | -1.360158 | -0.709091 |
| 565 | 1.704854 | 2.085134 | 1.615931 | 1.723842 | 0.102458 | -0.017833 | 0.693043 | 1.263669 | -0.217664 | -1.058611 | ... | 1.536720 | 2.047399 | 1.421940 | 1.494959 | -0.691230 | -0.394820 | 0.236573 | 0.733827 | -0.531855 | -0.973978 |
| 566 | 0.702284 | 2.045574 | 0.672676 | 0.577953 | -0.840484 | -0.038680 | 0.046588 | 0.105777 | -0.809117 | -0.895587 | ... | 0.561361 | 1.374854 | 0.579001 | 0.427906 | -0.809587 | 0.350735 | 0.326767 | 0.414069 | -1.104549 | -0.318409 |
| 567 | 1.838341 | 2.336457 | 1.982524 | 1.735218 | 1.525767 | 3.272144 | 3.296944 | 2.658866 | 2.137194 | 1.043695 | ... | 1.961239 | 2.237926 | 2.303601 | 1.653171 | 1.430427 | 3.904848 | 3.197605 | 2.289985 | 1.919083 | 2.219635 |
| 568 | -1.808401 | 1.221792 | -1.814389 | -1.347789 | -3.112085 | -1.150752 | -1.114873 | -1.261820 | -0.820070 | -0.561032 | ... | -1.410893 | 0.764190 | -1.432735 | -1.075813 | -1.859019 | -1.207552 | -1.305831 | -1.745063 | -0.048138 | -0.751207 |
5 lignes × 30 colonnes
-
Voici maintenant la partie critique, les prochaines lignes de code vont projeter les données sur le cancer du sein en deux dimensions.
principal components.Vous utiliserez la bibliothèque sklearn pour importer le module
PCA, et dans la méthode PCA, vous indiquerez le nombre de composantes (n_components=2) et appellerez enfin fit_transform sur les données agrégées. Ici, plusieurs composants représentent la dimension inférieure dans laquelle vous projetterez vos données de dimension supérieure.
from sklearn.decomposition import PCA
pca_breast = PCA(n_components=2)
principalComponents_breast = pca_breast.fit_transform(x)
Ensuite, créons un DataFrame qui contiendra les valeurs des composantes principales pour les 569 échantillons.
principal_breast_Df = pd.DataFrame(data = principalComponents_breast
, columns = ['principal component 1', 'principal component 2'])
principal_breast_Df.tail()
| composante principale 1 | composante principale 2 | |
|---|---|---|
| 564 | 6.439315 | -3.576817 |
| 565 | 3.793382 | -3.584048 |
| 566 | 1.256179 | -1.902297 |
| 567 | 10.374794 | 1.672010 |
| 568 | -5.475243 | -0.670637 |
- Une fois que vous avez les composantes principales, vous pouvez trouver le
explained_variance_ratio. Il vous indique la quantité d'informations ou la variance que chaque composante principale contient après avoir projeté les données dans un sous-espace de dimension inférieure.
print('Explained variability per principal component: {}'.format(pca_breast.explained_variance_ratio_))
Explained variability per principal component: [0.44272026 0.18971182]
Dans le résultat ci-dessus, vous pouvez observer que le site principal component 1 contient 44,2 % des informations, tandis que le site principal component 2 n'en contient que 19 %. L'autre point à noter est qu'en projetant des données à trente dimensions sur des données à deux dimensions, 36,8 % des informations ont été perdues.
Traçons la visualisation des 569 échantillons le long des axes principal component - 1 et principal component - 2. Cela devrait vous donner un bon aperçu de la façon dont vos échantillons sont répartis entre les deux classes.
plt.figure()
plt.figure(figsize=(10,10))
plt.xticks(fontsize=12)
plt.yticks(fontsize=14)
plt.xlabel('Principal Component - 1',fontsize=20)
plt.ylabel('Principal Component - 2',fontsize=20)
plt.title("Principal Component Analysis of Breast Cancer Dataset",fontsize=20)
targets = ['Benign', 'Malignant']
colors = ['r', 'g']
for target, color in zip(targets,colors):
indicesToKeep = breast_dataset['label'] == target
plt.scatter(principal_breast_Df.loc[indicesToKeep, 'principal component 1']
, principal_breast_Df.loc[indicesToKeep, 'principal component 2'], c = color, s = 50)
plt.legend(targets,prop={'size': 15})
<matplotlib.legend.Legend at 0x14552a630>
<Figure size 432x288 with 0 Axes>
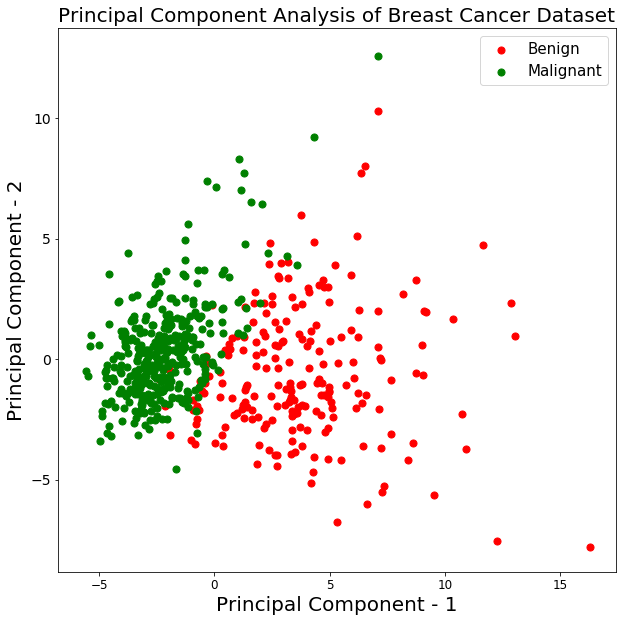
Le graphique ci-dessus montre que les deux classes benign et malignant, lorsqu'elles sont projetées dans un espace à deux dimensions, peuvent être séparées linéairement jusqu'à un certain point. On peut également observer que la classe benign est plus dispersée que la classe malignant.
Visualisation des données CIFAR - 10
Les lignes de code suivantes pour la visualisation des données CIFAR-10 sont assez similaires à la visualisation de l'ACP des données sur le cancer du sein.
- Vérifions rapidement les valeurs maximales et minimales des images d'entraînement CIFAR-10 et des pixels compris entre 0 et 1 inclus.
normalizeles pixels compris entre 0 et 1 inclus.
np.min(x_train),np.max(x_train)
(0.0, 1.0)
x_train = x_train/255.0
np.min(x_train),np.max(x_train)
(0.0, 0.00392156862745098)
x_train.shape
(50000, 32, 32, 3)
Ensuite, vous allez créer un DataFrame qui contiendra les valeurs en pixels des images ainsi que leurs étiquettes respectives dans un format ligne-colonne.
Mais avant cela, modifions les dimensions de l'image de trois à un (aplatissez les images).
x_train_flat = x_train.reshape(-1,3072)
feat_cols = ['pixel'+str(i) for i in range(x_train_flat.shape[1])]
df_cifar = pd.DataFrame(x_train_flat,columns=feat_cols)
df_cifar['label'] = y_train
print('Size of the dataframe: {}'.format(df_cifar.shape))
Size of the dataframe: (50000, 3073)
Parfait ! La taille du DataFrame est correcte puisqu'il y a 50 000 images d'apprentissage, chacune ayant 3072 pixels et une colonne supplémentaire pour les étiquettes, soit au total 3073.
L'ACP sera appliquée à toutes les colonnes, à l'exception de la dernière, qui correspond à l'étiquette de chaque image.
df_cifar.head()
| pixel0 | pixel1 | pixel2 | pixel3 | pixel4 | pixel5 | pixel6 | pixel7 | pixel8 | pixel9 | ... | pixel3063 | pixel3064 | pixel3065 | pixel3066 | pixel3067 | pixel3068 | pixel3069 | pixel3070 | pixel3071 | étiquette | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.231373 | 0.243137 | 0.247059 | 0.168627 | 0.180392 | 0.176471 | 0.196078 | 0.188235 | 0.168627 | 0.266667 | ... | 0.847059 | 0.721569 | 0.549020 | 0.592157 | 0.462745 | 0.329412 | 0.482353 | 0.360784 | 0.282353 | 6 |
| 1 | 0.603922 | 0.694118 | 0.733333 | 0.494118 | 0.537255 | 0.533333 | 0.411765 | 0.407843 | 0.372549 | 0.400000 | ... | 0.560784 | 0.521569 | 0.545098 | 0.560784 | 0.525490 | 0.556863 | 0.560784 | 0.521569 | 0.564706 | 9 |
| 2 | 1.000000 | 1.000000 | 1.000000 | 0.992157 | 0.992157 | 0.992157 | 0.992157 | 0.992157 | 0.992157 | 0.992157 | ... | 0.305882 | 0.333333 | 0.325490 | 0.309804 | 0.333333 | 0.325490 | 0.313725 | 0.337255 | 0.329412 | 9 |
| 3 | 0.109804 | 0.098039 | 0.039216 | 0.145098 | 0.133333 | 0.074510 | 0.149020 | 0.137255 | 0.078431 | 0.164706 | ... | 0.211765 | 0.184314 | 0.109804 | 0.247059 | 0.219608 | 0.145098 | 0.282353 | 0.254902 | 0.180392 | 4 |
| 4 | 0.666667 | 0.705882 | 0.776471 | 0.658824 | 0.698039 | 0.768627 | 0.694118 | 0.725490 | 0.796078 | 0.717647 | ... | 0.294118 | 0.309804 | 0.321569 | 0.278431 | 0.294118 | 0.305882 | 0.286275 | 0.301961 | 0.313725 | 1 |
5 lignes × 3073 colonnes
- Ensuite, vous allez créer la méthode PCA et passer le nombre de composantes à deux et appliquer
fit_transformsur les données d'entraînement, ce qui peut prendre quelques secondes puisqu'il y a 50 000 échantillons.
pca_cifar = PCA(n_components=2)
principalComponents_cifar = pca_cifar.fit_transform(df_cifar.iloc[:,:-1])
Ensuite, vous convertirez les composantes principales pour chacune des 50 000 images d'un tableau numpy à un DataFrame pandas.
principal_cifar_Df = pd.DataFrame(data = principalComponents_cifar
, columns = ['principal component 1', 'principal component 2'])
principal_cifar_Df['y'] = y_train
principal_cifar_Df.head()
| composante principale 1 | composante principale 2 | y | |
|---|---|---|---|
| 0 | -6.401018 | 2.729039 | 6 |
| 1 | 0.829783 | -0.949943 | 9 |
| 2 | 7.730200 | -11.522102 | 9 |
| 3 | -10.347817 | 0.010738 | 4 |
| 4 | -2.625651 | -4.969240 | 1 |
- Déterminons rapidement la quantité d'informations ou
varianceque contiennent les composantes principales.
print('Explained variability per principal component: {}'.format(pca_cifar.explained_variance_ratio_))
Explained variability per principal component: [0.2907663 0.11253144]
Il semble qu'une bonne quantité d'informations ait été conservée par les composantes principales 1 et 2, étant donné que les données ont été projetées de 3072 dimensions à seulement deux composantes principales.
Il est temps de visualiser les données CIFAR-10 dans un espace bidimensionnel. N'oubliez pas qu'il existe un certain chevauchement des classes sémantiques dans cet ensemble de données, ce qui signifie qu'une grenouille peut avoir une forme légèrement similaire à celle d'un chat ou un cerf à celle d'un chien, en particulier lorsqu'ils sont projetés dans un espace bidimensionnel. Les différences entre les deux ne sont pas toujours bien perçues.
import seaborn as sns
plt.figure(figsize=(16,10))
sns.scatterplot(
x="principal component 1", y="principal component 2",
hue="y",
palette=sns.color_palette("hls", 10),
data=principal_cifar_Df,
legend="full",
alpha=0.3
)
<matplotlib.axes._subplots.AxesSubplot at 0x12a5ba8d0>
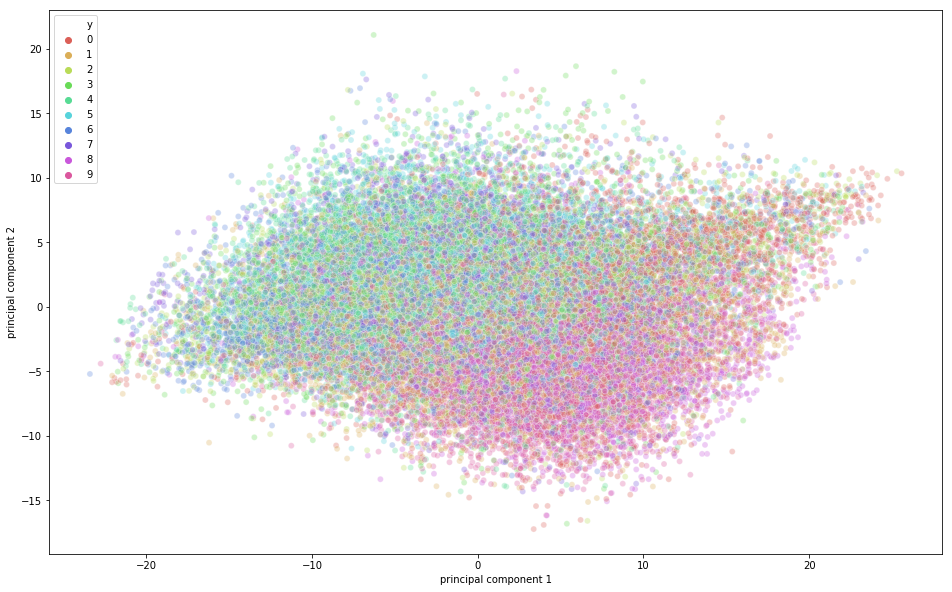
Sur la figure ci-dessus, vous pouvez observer qu'une certaine variation a été capturée par les composantes principales puisqu'il existe une certaine structure dans les points lorsqu'ils sont projetés le long de l'axe des deux composantes principales. Les points appartenant à la même classe sont proches les uns des autres, et les points ou images très différents sur le plan sémantique sont plus éloignés les uns des autres.
Accélérer la formation en apprentissage profond à l'aide de l'ACP
Dans ce dernier segment du tutoriel, vous apprendrez comment accélérer le processus de formation de votre modèle d'apprentissage profond à l'aide de l'ACP.
Note: Pour apprendre les termes de base qui seront utilisés dans cette section, n'hésitez pas à consulter ce tutoriel.
Tout d'abord, normalisons les images d'apprentissage et de test. Si vous vous souvenez bien, les images d'apprentissage ont été normalisées dans la partie visualisation de l'ACP, il vous suffit donc de normaliser les images de test. C'est donc ce que nous allons faire rapidement !
x_test = x_test/255.0
x_test = x_test.reshape(-1,32,32,3)
reshape les données de test.
x_test_flat = x_test.reshape(-1,3072)
Ensuite, vous allez créer l'instance du modèle PCA.
Ici, vous pouvez également indiquer la quantité de variance que vous souhaitez que l'ACP capture. Passons 0,9 comme paramètre du modèle ACP, ce qui signifie que l'ACP retiendra 90 % de la variance et que le site number of components nécessaire pour capturer 90 % de la variance sera utilisé.
Notez que vous avez précédemment passé n_components en tant que paramètre et que vous avez ainsi pu déterminer la part de variance capturée par ces deux composantes. Mais ici, nous mentionnons explicitement le degré de variance que nous souhaitons que l'ACP capture et, par conséquent, le site n_components variera en fonction du paramètre de variance.
Si vous ne transmettez aucune variance, le nombre de composantes sera égal à la dimension originale des données.
pca = PCA(0.9)
Ensuite, vous adapterez l'instance PCA aux images d'apprentissage.
pca.fit(x_train_flat)
PCA(copy=True, iterated_power='auto', n_components=0.9, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
Déterminons maintenant combien de n_components l'ACP a utilisé pour capturer 0,9 variance.
pca.n_components_
99
Le résultat ci-dessus montre que pour obtenir une variance de 90 %, la dimension a été réduite à 99 composantes principales à partir des dimensions réelles 3072.
Enfin, vous appliquerez transform à l'ensemble de formation et de test pour générer un ensemble de données transformé à partir des paramètres générés par la méthode fit.
train_img_pca = pca.transform(x_train_flat)
test_img_pca = pca.transform(x_test_flat)
Ensuite, importons rapidement les bibliothèques nécessaires à l'exécution du modèle d'apprentissage profond.
from keras.models import Sequential
from keras.layers import Dense
from keras.utils import np_utils
from keras.optimizers import RMSprop
Vous allez maintenant convertir vos étiquettes d'apprentissage et de test en un vecteur d'encodage à un coup.
y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
Définissons le nombre d'époques, le nombre de classes et la taille du lot pour votre modèle.
batch_size = 128
num_classes = 10
epochs = 20
Ensuite, vous définirez votre modèle Sequential!
model = Sequential()
model.add(Dense(1024, activation='relu', input_shape=(99,)))
model.add(Dense(1024, activation='relu'))
model.add(Dense(512, activation='relu'))
model.add(Dense(256, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
Imprimons le résumé du modèle.
model.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 1024) 102400
_________________________________________________________________
dense_2 (Dense) (None, 1024) 1049600
_________________________________________________________________
dense_3 (Dense) (None, 512) 524800
_________________________________________________________________
dense_4 (Dense) (None, 256) 131328
_________________________________________________________________
dense_5 (Dense) (None, 10) 2570
=================================================================
Total params: 1,810,698
Trainable params: 1,810,698
Non-trainable params: 0
_________________________________________________________________
Enfin, il est temps de compiler et de former le modèle !
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
history = model.fit(train_img_pca, y_train,batch_size=batch_size,epochs=epochs,verbose=1,
validation_data=(test_img_pca, y_test))
WARNING:tensorflow:From /Users/adityasharma/blog/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:2704: calling reduce_sum (from tensorflow.python.ops.math_ops) with keep_dims is deprecated and will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead
WARNING:tensorflow:From /Users/adityasharma/blog/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:1257: calling reduce_mean (from tensorflow.python.ops.math_ops) with keep_dims is deprecated and will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead
Train on 50000 samples, validate on 10000 samples
Epoch 1/20
50000/50000 [==============================] - 7s - loss: 1.9032 - acc: 0.2962 - val_loss: 1.6925 - val_acc: 0.3875
Epoch 2/20
50000/50000 [==============================] - 7s - loss: 1.6480 - acc: 0.4055 - val_loss: 1.5313 - val_acc: 0.4412
Epoch 3/20
50000/50000 [==============================] - 7s - loss: 1.5205 - acc: 0.4534 - val_loss: 1.4609 - val_acc: 0.4695
Epoch 4/20
50000/50000 [==============================] - 7s - loss: 1.4322 - acc: 0.4849 - val_loss: 1.6164 - val_acc: 0.4503
Epoch 5/20
50000/50000 [==============================] - 7s - loss: 1.3621 - acc: 0.5120 - val_loss: 1.3626 - val_acc: 0.5081
Epoch 6/20
50000/50000 [==============================] - 7s - loss: 1.2995 - acc: 0.5330 - val_loss: 1.4100 - val_acc: 0.4940
Epoch 7/20
50000/50000 [==============================] - 7s - loss: 1.2473 - acc: 0.5529 - val_loss: 1.3589 - val_acc: 0.5251
Epoch 8/20
50000/50000 [==============================] - 7s - loss: 1.2010 - acc: 0.5669 - val_loss: 1.3315 - val_acc: 0.5232
Epoch 9/20
50000/50000 [==============================] - 7s - loss: 1.1524 - acc: 0.5868 - val_loss: 1.3903 - val_acc: 0.5197
Epoch 10/20
50000/50000 [==============================] - 7s - loss: 1.1134 - acc: 0.6013 - val_loss: 1.2722 - val_acc: 0.5499
Epoch 11/20
50000/50000 [==============================] - 7s - loss: 1.0691 - acc: 0.6160 - val_loss: 1.5911 - val_acc: 0.4768
Epoch 12/20
50000/50000 [==============================] - 7s - loss: 1.0325 - acc: 0.6289 - val_loss: 1.2515 - val_acc: 0.5602
Epoch 13/20
50000/50000 [==============================] - 7s - loss: 0.9977 - acc: 0.6420 - val_loss: 1.5678 - val_acc: 0.4914
Epoch 14/20
50000/50000 [==============================] - 8s - loss: 0.9567 - acc: 0.6567 - val_loss: 1.3525 - val_acc: 0.5418
Epoch 15/20
50000/50000 [==============================] - 9s - loss: 0.9158 - acc: 0.6713 - val_loss: 1.3525 - val_acc: 0.5540
Epoch 16/20
50000/50000 [==============================] - 10s - loss: 0.8948 - acc: 0.6816 - val_loss: 1.5633 - val_acc: 0.5156
Epoch 17/20
50000/50000 [==============================] - 9s - loss: 0.8690 - acc: 0.6903 - val_loss: 1.6980 - val_acc: 0.5084
Epoch 18/20
50000/50000 [==============================] - 9s - loss: 0.8586 - acc: 0.7002 - val_loss: 1.6325 - val_acc: 0.5247
Epoch 19/20
50000/50000 [==============================] - 8s - loss: 0.9367 - acc: 0.6853 - val_loss: 1.8253 - val_acc: 0.5165
Epoch 20/20
50000/50000 [==============================] - 8s - loss: 2.3761 - acc: 0.5971 - val_loss: 6.0192 - val_acc: 0.4409
D'après le résultat ci-dessus, vous pouvez observer que le temps nécessaire à l'apprentissage de chaque époch est de seulement 7 seconds sur un processeur. Le modèle a fait un travail décent sur les données d'apprentissage, obtenant une précision de 70%, alors qu'il n'a obtenu qu'une précision de 56% sur les données de test. Cela signifie qu'il a surajouté les données d'apprentissage. Cependant, n'oubliez pas que les données ont été projetées sur 99 dimensions à partir de 3072 dimensions et que, malgré cela, il a fait un excellent travail !
Enfin, voyons combien de temps il faut au modèle pour s'entraîner sur l'ensemble de données original et quelle précision il peut atteindre en utilisant le même modèle d'apprentissage profond.
model = Sequential()
model.add(Dense(1024, activation='relu', input_shape=(3072,)))
model.add(Dense(1024, activation='relu'))
model.add(Dense(512, activation='relu'))
model.add(Dense(256, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
history = model.fit(x_train_flat, y_train,batch_size=batch_size,epochs=epochs,verbose=1,
validation_data=(x_test_flat, y_test))
Train on 50000 samples, validate on 10000 samples
Epoch 1/20
50000/50000 [==============================] - 23s - loss: 2.0657 - acc: 0.2200 - val_loss: 2.0277 - val_acc: 0.2485
Epoch 2/20
50000/50000 [==============================] - 22s - loss: 1.8727 - acc: 0.3166 - val_loss: 1.8428 - val_acc: 0.3215
Epoch 3/20
50000/50000 [==============================] - 22s - loss: 1.7801 - acc: 0.3526 - val_loss: 1.7657 - val_acc: 0.3605
Epoch 4/20
50000/50000 [==============================] - 22s - loss: 1.7141 - acc: 0.3796 - val_loss: 1.6345 - val_acc: 0.4132
Epoch 5/20
50000/50000 [==============================] - 22s - loss: 1.6566 - acc: 0.4001 - val_loss: 1.6384 - val_acc: 0.4076
Epoch 6/20
50000/50000 [==============================] - 22s - loss: 1.6083 - acc: 0.4209 - val_loss: 1.7507 - val_acc: 0.3574
Epoch 7/20
50000/50000 [==============================] - 22s - loss: 1.5626 - acc: 0.4374 - val_loss: 1.7125 - val_acc: 0.4010
Epoch 8/20
50000/50000 [==============================] - 22s - loss: 1.5252 - acc: 0.4486 - val_loss: 1.5914 - val_acc: 0.4321
Epoch 9/20
50000/50000 [==============================] - 24s - loss: 1.4924 - acc: 0.4620 - val_loss: 1.5352 - val_acc: 0.4616
Epoch 10/20
50000/50000 [==============================] - 25s - loss: 1.4627 - acc: 0.4728 - val_loss: 1.4561 - val_acc: 0.4798
Epoch 11/20
50000/50000 [==============================] - 24s - loss: 1.4349 - acc: 0.4820 - val_loss: 1.5044 - val_acc: 0.4723
Epoch 12/20
50000/50000 [==============================] - 24s - loss: 1.4120 - acc: 0.4919 - val_loss: 1.4740 - val_acc: 0.4790
Epoch 13/20
50000/50000 [==============================] - 23s - loss: 1.3913 - acc: 0.4981 - val_loss: 1.4430 - val_acc: 0.4891
Epoch 14/20
50000/50000 [==============================] - 27s - loss: 1.3678 - acc: 0.5098 - val_loss: 1.4323 - val_acc: 0.4888
Epoch 15/20
50000/50000 [==============================] - 27s - loss: 1.3508 - acc: 0.5148 - val_loss: 1.6179 - val_acc: 0.4372
Epoch 16/20
50000/50000 [==============================] - 25s - loss: 1.3443 - acc: 0.5167 - val_loss: 1.5868 - val_acc: 0.4656
Epoch 17/20
50000/50000 [==============================] - 25s - loss: 1.3734 - acc: 0.5101 - val_loss: 1.4756 - val_acc: 0.4913
Epoch 18/20
50000/50000 [==============================] - 26s - loss: 5.5126 - acc: 0.3591 - val_loss: 5.7580 - val_acc: 0.3084
Epoch 19/20
50000/50000 [==============================] - 27s - loss: 5.6346 - acc: 0.3395 - val_loss: 3.7362 - val_acc: 0.3402
Epoch 20/20
50000/50000 [==============================] - 26s - loss: 6.4199 - acc: 0.3030 - val_loss: 13.9429 - val_acc: 0.1326
Voilà ! D'après les résultats ci-dessus, il est évident que le temps nécessaire à l'apprentissage de chaque époch est d'environ 23 seconds sur une unité centrale, soit près de trois fois plus que le modèle formé à partir des résultats de l'ACP.
En outre, la précision de l'entraînement et du test est inférieure à celle que vous avez obtenue avec les 99 composantes principales en entrée du modèle.
Ainsi, en appliquant l'ACP aux données d'apprentissage, vous avez pu former votre algorithme d'apprentissage profond non seulement à l'adresse fast, mais aussi à une meilleure adresse accuracy sur les données de test, par rapport à l'algorithme d'apprentissage profond formé avec les données d'apprentissage originales.
Allez plus loin !
Félicitations pour avoir terminé le tutoriel.
Ce tutoriel était une excellente et complète introduction à l'ACP en Python, qui couvrait à la fois les concepts théoriques et pratiques de l'ACP.
Si vous souhaitez approfondir les techniques de réduction de la dimensionnalité, vous pouvez vous renseigner sur le t-distributed Stochastic Neighbor Embedding, communément appelé tSNE, qui est une technique probabiliste non linéaire de réduction de la dimensionnalité.
Si vous souhaitez en savoir plus sur les techniques d'apprentissage non supervisé comme l'ACP, suivez le cours Unsupervised Learning in Python de DataCamp.
Références pour la poursuite de l'apprentissage :
Questions fréquemment posées
Quelle est la différence entre l'analyse factorielle et l'analyse en composantes principales ?
L'analyse factorielle (AF) et l'analyse en composantes principales (ACP) sont toutes deux des techniques utilisées pour réduire la dimensionnalité, mais elles ont des objectifs différents. L'ACP vise à préserver la variabilité totale des données en les transformant en un nouvel ensemble de variables non corrélées (composantes principales), classées en fonction de la variance qu'elles expliquent. En revanche, l'AF vise à identifier les relations sous-jacentes entre les variables observées en modélisant les données à l'aide de quelques facteurs latents qui expliquent les corrélations entre les variables.
Qu'est-ce que l'analyse en composantes principales ?
L'analyse en composantes principales consiste à trouver les vecteurs propres de la matrice de covariance des données afin de les projeter dans un espace de dimension inférieure défini par les composantes principales (celles qui ont les valeurs propres les plus élevées).