Curso
Execute e edite o código deste tutorial online
Executar códigoA análise de componentes principais (PCA) é uma técnica de redução de dimensionalidade linear que pode ser usada para extrair informações de um espaço de alta dimensão, projetando-as em um subespaço de dimensão inferior. Ele tenta preservar as partes essenciais que têm mais variabilidade nos dados e remover as partes não essenciais com menos variabilidade.
As dimensões nada mais são do que recursos que representam os dados. Por exemplo, uma imagem de 28 x 28 tem 784 elementos de imagem (pixels), que são as dimensões ou os recursos que, juntos, representam essa imagem.
Uma coisa importante a ser observada sobre a PCA é que ela é uma técnica de redução de dimensionalidade não supervisionada, você pode agrupar os pontos de dados semelhantes com base na correlação de recursos entre eles sem nenhuma supervisão (ou rótulos), e você aprenderá como fazer isso de forma prática usando Python nas seções posteriores deste tutorial!
De acordo com a Wikipedia, a ACP é um procedimento estatístico que usa uma transformação ortogonal para converter um conjunto de observações de variáveis possivelmente correlacionadas (entidades em que cada uma delas assume vários valores numéricos) em um conjunto de valores de variáveis linearmente não correlacionadas chamadas de componentes principais.
Observação: Features, Dimensions e Variables se referem à mesma coisa. Você verá que eles são usados de forma intercambiável.
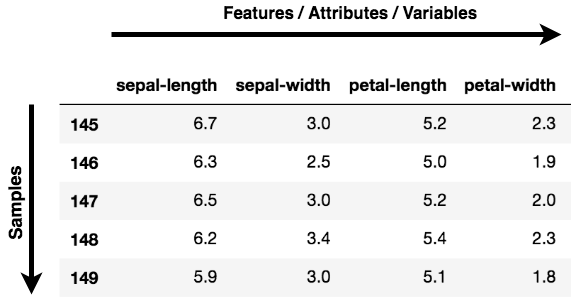
Onde você pode aplicar a PCA?
-
Visualização de dados: Ao trabalhar em qualquer problema relacionado a dados, o desafio no mundo atual é o grande volume de dados e as variáveis/características que definem esses dados. Para resolver um problema em que os dados são a chave, você precisa de uma exploração extensiva dos dados, como descobrir como as variáveis estão correlacionadas ou entender a distribuição de algumas variáveis. Considerando que há um grande número de variáveis ou dimensões ao longo das quais os dados são distribuídos, a visualização pode ser um desafio e quase impossível.
Portanto, a PCA pode fazer isso por você, pois projeta os dados em uma dimensão inferior, permitindo assim que você visualize os dados em um espaço 2D ou 3D a olho nu.
-
Acelerando um algoritmo de aprendizado de máquina (ML): Como a ideia principal do PCA é a redução da dimensionalidade, você pode aproveitá-la para acelerar o tempo de treinamento e teste do algoritmo de aprendizado de máquina, considerando que seus dados têm muitos recursos e o aprendizado do algoritmo de ML é muito lento.
Em um nível abstrato, você pega um conjunto de dados com muitos recursos e simplifica esse conjunto de dados selecionando alguns Principal Components dos recursos originais.
O que é um componente principal?
Os componentes principais são a chave para a PCA; eles representam o que está por trás dos dados. Em um termo leigo, quando os dados são projetados em uma dimensão mais baixa (suponha três dimensões) a partir de um espaço mais alto, as três dimensões nada mais são do que os três componentes principais que capturam (ou mantêm) a maior parte da variação (informações) dos seus dados.
Os componentes principais têm direção e magnitude. A direção representa em quais eixos principais os dados estão mais espalhados ou têm maior variação e a magnitude significa a quantidade de variação que o componente principal captura dos dados quando projetados nesse eixo. Os componentes principais são uma linha reta, e o primeiro componente principal contém a maior variação nos dados. Cada componente principal subsequente é ortogonal ao anterior e tem uma variação menor. Dessa forma, com um conjunto de x variáveis correlacionadas em y amostras, você obtém um conjunto de u componentes principais não correlacionados nas mesmas y amostras.
O motivo pelo qual você obtém componentes principais não correlacionados a partir dos recursos originais é que os recursos correlacionados contribuem para o mesmo componente principal, reduzindo assim os recursos de dados originais em componentes principais não correlacionados, cada um representando um conjunto diferente de recursos correlacionados com diferentes quantidades de variabilidade. Cada componente principal representa uma porcentagem da variabilidade total capturada dos dados.
No tutorial de hoje, aplicaremos a PCA com o objetivo de obter insights por meio da visualização de dados, e também aplicaremos a PCA com o objetivo de acelerar nosso algoritmo de aprendizado de máquina. Para realizar as duas tarefas acima, você usará dois conjuntos de dados famosos: Câncer de mama e CIFAR - 10. O primeiro é um conjunto de dados numéricos; o segundo é um conjunto de dados de imagens.
Entendendo os dados
Antes de ir em frente e carregar os dados, é bom entender e analisar os dados com os quais você trabalhará!
Câncer de mama
O conjunto de dados de câncer de mama é um dado multivariado de valor real que consiste em duas classes, em que cada classe significa se uma paciente tem ou não câncer de mama. As duas categorias são: maligna e benigna.
A classe maligna tem 212 amostras, enquanto a classe benigna tem 357 amostras.
Ele tem 30 recursos compartilhados em todas as classes: raio, textura, perímetro, área, suavidade, dimensão fractal, etc.
Você pode fazer o download do conjunto de dados de câncer de mama aqui ou, de maneira mais fácil, carregá-lo com a ajuda da biblioteca sklearn.
CIFAR - 10
O conjunto de dados CIFAR-10 (Canadian Institute For Advanced Research) consiste em 60000 imagens, cada uma com 32x32x3 imagens coloridas, com dez classes, com 6000 imagens por categoria.
O conjunto de dados consiste em 50000 imagens de treinamento e 10000 imagens de teste.
As classes do conjunto de dados são: avião, automóvel, pássaro, gato, veado, cachorro, sapo, cavalo, navio, caminhão.
Você pode fazer o download do conjunto de dados do CIFAR aqui ou também pode carregá-lo rapidamente com a ajuda de uma biblioteca de aprendizagem profunda, como Keras.
Exploração de dados usando PCA
Agora você carregará e analisará os conjuntos de dados Breast Cancer e CIFAR-10. A esta altura, você já tem uma ideia da dimensionalidade dos dois conjuntos de dados.
Então, vamos explorar rapidamente os dois conjuntos de dados.
Exploração de dados sobre câncer de mama
Primeiro, vamos explorar o conjunto de dados Breast Cancer.
Você usará o módulo sklearn's datasets e importará o conjunto de dados Breast Cancer a partir dele.
from sklearn.datasets import load_breast_cancer
load_breast_cancer fornecerá a você os rótulos e os dados. Para obter os dados, você chamará .data e, para obter os rótulos, .target.
Os dados têm 569 amostras com trinta recursos, e cada amostra tem um rótulo associado a ela. Há dois rótulos nesse conjunto de dados.
breast = load_breast_cancer()
breast_data = breast.data
Vamos verificar a forma dos dados.
breast_data.shape
(569, 30)
Embora para este tutorial você não precise dos rótulos, para entender melhor, vamos carregar os rótulos e verificar a forma.
breast_labels = breast.target
breast_labels.shape
(569,)
Agora você importará o numpy, pois reformulará o breast_labels para concatená-lo com o breast_data, de modo que possa finalmente criar um DataFrame que terá os dados e os rótulos.
import numpy as np
labels = np.reshape(breast_labels,(569,1))
Depois de reshaping os rótulos, você concatenate os dados e os rótulos ao longo do segundo eixo, o que significa que a forma final da matriz será 569 x 31.
final_breast_data = np.concatenate([breast_data,labels],axis=1)
final_breast_data.shape
(569, 31)
Agora você importará pandas para criar o DataFrame dos dados finais para representar os dados de forma tabular.
import pandas as pd
breast_dataset = pd.DataFrame(final_breast_data)
Vamos imprimir rapidamente os recursos que existem no conjunto de dados de câncer de mama!
features = breast.feature_names
features
array(['mean radius', 'mean texture', 'mean perimeter', 'mean area',
'mean smoothness', 'mean compactness', 'mean concavity',
'mean concave points', 'mean symmetry', 'mean fractal dimension',
'radius error', 'texture error', 'perimeter error', 'area error',
'smoothness error', 'compactness error', 'concavity error',
'concave points error', 'symmetry error',
'fractal dimension error', 'worst radius', 'worst texture',
'worst perimeter', 'worst area', 'worst smoothness',
'worst compactness', 'worst concavity', 'worst concave points',
'worst symmetry', 'worst fractal dimension'], dtype='<U23')
Se você observar na matriz features, o campo label está ausente. Portanto, você terá que adicioná-lo manualmente à matriz features, pois estará equiparando essa matriz aos nomes das colunas do seu dataframe breast_dataset.
features_labels = np.append(features,'label')
Ótimo! Agora você incorporará os nomes das colunas ao quadro de dados breast_dataset.
breast_dataset.columns = features_labels
Vamos imprimir as primeiras linhas do dataframe.
breast_dataset.head()
| raio médio | textura média | perímetro médio | área média | suavidade média | compacidade média | concavidade média | pontos côncavos médios | simetria média | dimensão fractal média | ... | pior textura | pior perímetro | pior área | pior suavidade | pior compactação | pior concavidade | piores pontos côncavos | pior simetria | pior dimensão fractal | rótulo | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 17.99 | 10.38 | 122.80 | 1001.0 | 0.11840 | 0.27760 | 0.3001 | 0.14710 | 0.2419 | 0.07871 | ... | 17.33 | 184.60 | 2019.0 | 0.1622 | 0.6656 | 0.7119 | 0.2654 | 0.4601 | 0.11890 | 0.0 |
| 1 | 20.57 | 17.77 | 132.90 | 1326.0 | 0.08474 | 0.07864 | 0.0869 | 0.07017 | 0.1812 | 0.05667 | ... | 23.41 | 158.80 | 1956.0 | 0.1238 | 0.1866 | 0.2416 | 0.1860 | 0.2750 | 0.08902 | 0.0 |
| 2 | 19.69 | 21.25 | 130.00 | 1203.0 | 0.10960 | 0.15990 | 0.1974 | 0.12790 | 0.2069 | 0.05999 | ... | 25.53 | 152.50 | 1709.0 | 0.1444 | 0.4245 | 0.4504 | 0.2430 | 0.3613 | 0.08758 | 0.0 |
| 3 | 11.42 | 20.38 | 77.58 | 386.1 | 0.14250 | 0.28390 | 0.2414 | 0.10520 | 0.2597 | 0.09744 | ... | 26.50 | 98.87 | 567.7 | 0.2098 | 0.8663 | 0.6869 | 0.2575 | 0.6638 | 0.17300 | 0.0 |
| 4 | 20.29 | 14.34 | 135.10 | 1297.0 | 0.10030 | 0.13280 | 0.1980 | 0.10430 | 0.1809 | 0.05883 | ... | 16.67 | 152.20 | 1575.0 | 0.1374 | 0.2050 | 0.4000 | 0.1625 | 0.2364 | 0.07678 | 0.0 |
5 linhas × 31 colunas
Como os rótulos originais estão no formato 0,1, você alterará os rótulos para benign e malignant usando a função .replace. Você usará inplace=True que modificará o dataframe breast_dataset.
breast_dataset['label'].replace(0, 'Benign',inplace=True)
breast_dataset['label'].replace(1, 'Malignant',inplace=True)
Vamos imprimir as últimas linhas do site breast_dataset.
breast_dataset.tail()
| raio médio | textura média | perímetro médio | área média | suavidade média | compacidade média | concavidade média | pontos côncavos médios | simetria média | dimensão fractal média | ... | pior textura | pior perímetro | pior área | pior suavidade | pior compactação | pior concavidade | piores pontos côncavos | pior simetria | pior dimensão fractal | rótulo | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 564 | 21.56 | 22.39 | 142.00 | 1479.0 | 0.11100 | 0.11590 | 0.24390 | 0.13890 | 0.1726 | 0.05623 | ... | 26.40 | 166.10 | 2027.0 | 0.14100 | 0.21130 | 0.4107 | 0.2216 | 0.2060 | 0.07115 | Benigno |
| 565 | 20.13 | 28.25 | 131.20 | 1261.0 | 0.09780 | 0.10340 | 0.14400 | 0.09791 | 0.1752 | 0.05533 | ... | 38.25 | 155.00 | 1731.0 | 0.11660 | 0.19220 | 0.3215 | 0.1628 | 0.2572 | 0.06637 | Benigno |
| 566 | 16.60 | 28.08 | 108.30 | 858.1 | 0.08455 | 0.10230 | 0.09251 | 0.05302 | 0.1590 | 0.05648 | ... | 34.12 | 126.70 | 1124.0 | 0.11390 | 0.30940 | 0.3403 | 0.1418 | 0.2218 | 0.07820 | Benigno |
| 567 | 20.60 | 29.33 | 140.10 | 1265.0 | 0.11780 | 0.27700 | 0.35140 | 0.15200 | 0.2397 | 0.07016 | ... | 39.42 | 184.60 | 1821.0 | 0.16500 | 0.86810 | 0.9387 | 0.2650 | 0.4087 | 0.12400 | Benigno |
| 568 | 7.76 | 24.54 | 47.92 | 181.0 | 0.05263 | 0.04362 | 0.00000 | 0.00000 | 0.1587 | 0.05884 | ... | 30.37 | 59.16 | 268.6 | 0.08996 | 0.06444 | 0.0000 | 0.0000 | 0.2871 | 0.07039 | Maligno |
5 linhas × 31 colunas
CIFAR - 10 exploração de dados
Em seguida, você explorará o conjunto de dados de imagens CIFAR - 10
Você pode carregar o conjunto de dados CIFAR - 10 usando uma biblioteca de aprendizagem profunda chamada Keras.
from keras.datasets import cifar10
Depois de importados, você usará o método .load_data() para fazer download dos dados, que serão baixados e armazenados no diretório Keras. Isso pode levar algum tempo, dependendo da velocidade da sua Internet.
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
A linha de código acima retorna imagens de treinamento e teste junto com os rótulos.
Vamos imprimir rapidamente a forma das imagens de treinamento e teste.
print('Traning data shape:', x_train.shape)
print('Testing data shape:', x_test.shape)
Traning data shape: (50000, 32, 32, 3)
Testing data shape: (10000, 32, 32, 3)
Vamos também imprimir o formato das etiquetas.
y_train.shape,y_test.shape
((50000, 1), (10000, 1))
Vamos descobrir também o número total de rótulos e os vários tipos de classes que os dados têm.
# Find the unique numbers from the train labels
classes = np.unique(y_train)
nClasses = len(classes)
print('Total number of outputs : ', nClasses)
print('Output classes : ', classes)
Total number of outputs : 10
Output classes : [0 1 2 3 4 5 6 7 8 9]
Agora, para plotar as imagens CIFAR-10, você importará matplotlib e também usará um comando magic (%) %matplotlib inline para informar ao notebook jupyter para mostrar a saída dentro do próprio notebook!
import matplotlib.pyplot as plt
%matplotlib inline
Para que você entenda melhor, vamos criar um dicionário que terá nomes de classes com seus rótulos de classes categóricas correspondentes.
label_dict = {
0: 'airplane',
1: 'automobile',
2: 'bird',
3: 'cat',
4: 'deer',
5: 'dog',
6: 'frog',
7: 'horse',
8: 'ship',
9: 'truck',
}
plt.figure(figsize=[5,5])
# Display the first image in training data
plt.subplot(121)
curr_img = np.reshape(x_train[0], (32,32,3))
plt.imshow(curr_img)
print(plt.title("(Label: " + str(label_dict[y_train[0][0]]) + ")"))
# Display the first image in testing data
plt.subplot(122)
curr_img = np.reshape(x_test[0],(32,32,3))
plt.imshow(curr_img)
print(plt.title("(Label: " + str(label_dict[y_test[0][0]]) + ")"))
Text(0.5, 1.0, '(Label: frog)')
Text(0.5, 1.0, '(Label: cat)')

Mesmo que as duas imagens acima estejam borradas, você ainda pode observar que a primeira imagem é um sapo com o rótulo frog, enquanto a segunda imagem é de um gato com o rótulo cat.
Visualização de dados usando PCA
Agora vem a parte mais interessante deste tutorial. Como você aprendeu anteriormente que os projetos de PCA transformam dados de alta dimensão em um componente principal de baixa dimensão, agora é hora de visualizar isso com a ajuda do Python!
Visualização dos dados sobre câncer de mama
-
Você começa pelos
Standardizingvocê começa pelos dados, pois o resultado da PCA é influenciado com base na escala dos recursos dos dados.É uma prática comum normalizar seus dados antes de alimentá-los com qualquer algoritmo de aprendizado de máquina.
Para aplicar a normalização, você importará o módulo
StandardScalerda biblioteca sklearn e selecionará somente os recursos do sitebreast_datasetque você criou na etapa Exploração de dados. Depois de obter os recursos, você aplicará o dimensionamento fazendofit_transformnos dados dos recursos.Ao aplicar o StandardScaler, cada recurso dos seus dados deve ser distribuído normalmente, de modo que você dimensione a distribuição para uma média de zero e um desvio padrão de um.
from sklearn.preprocessing import StandardScaler
x = breast_dataset.loc[:, features].values
x = StandardScaler().fit_transform(x) # normalizing the features
x.shape
(569, 30)
Vamos verificar se os dados normalizados têm uma média de zero e um desvio padrão de um.
np.mean(x),np.std(x)
(-6.826538293184326e-17, 1.0)
Vamos converter os recursos normalizados em um formato tabular com a ajuda do DataFrame.
feat_cols = ['feature'+str(i) for i in range(x.shape[1])]
normalised_breast = pd.DataFrame(x,columns=feat_cols)
normalised_breast.tail()
| recurso0 | recurso1 | recurso2 | recurso3 | recurso4 | recurso5 | recurso6 | recurso7 | recurso8 | recurso9 | ... | feature20 | feature21 | feature22 | feature23 | feature24 | feature25 | feature26 | feature27 | feature28 | recurso29 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 564 | 2.110995 | 0.721473 | 2.060786 | 2.343856 | 1.041842 | 0.219060 | 1.947285 | 2.320965 | -0.312589 | -0.931027 | ... | 1.901185 | 0.117700 | 1.752563 | 2.015301 | 0.378365 | -0.273318 | 0.664512 | 1.629151 | -1.360158 | -0.709091 |
| 565 | 1.704854 | 2.085134 | 1.615931 | 1.723842 | 0.102458 | -0.017833 | 0.693043 | 1.263669 | -0.217664 | -1.058611 | ... | 1.536720 | 2.047399 | 1.421940 | 1.494959 | -0.691230 | -0.394820 | 0.236573 | 0.733827 | -0.531855 | -0.973978 |
| 566 | 0.702284 | 2.045574 | 0.672676 | 0.577953 | -0.840484 | -0.038680 | 0.046588 | 0.105777 | -0.809117 | -0.895587 | ... | 0.561361 | 1.374854 | 0.579001 | 0.427906 | -0.809587 | 0.350735 | 0.326767 | 0.414069 | -1.104549 | -0.318409 |
| 567 | 1.838341 | 2.336457 | 1.982524 | 1.735218 | 1.525767 | 3.272144 | 3.296944 | 2.658866 | 2.137194 | 1.043695 | ... | 1.961239 | 2.237926 | 2.303601 | 1.653171 | 1.430427 | 3.904848 | 3.197605 | 2.289985 | 1.919083 | 2.219635 |
| 568 | -1.808401 | 1.221792 | -1.814389 | -1.347789 | -3.112085 | -1.150752 | -1.114873 | -1.261820 | -0.820070 | -0.561032 | ... | -1.410893 | 0.764190 | -1.432735 | -1.075813 | -1.859019 | -1.207552 | -1.305831 | -1.745063 | -0.048138 | -0.751207 |
5 linhas × 30 colunas
-
Agora vem a parte crítica: as próximas linhas de código projetarão os dados tridimensionais do câncer de mama em dados bidimensionais
principal components.Você usará a biblioteca sklearn para importar o módulo
PCAe, no método PCA, você passará o número de componentes (n_components=2) e, por fim, chamará fit_transform nos dados agregados. Aqui, vários componentes representam a dimensão inferior na qual você projetará seus dados de dimensão superior.
from sklearn.decomposition import PCA
pca_breast = PCA(n_components=2)
principalComponents_breast = pca_breast.fit_transform(x)
Em seguida, vamos criar um DataFrame que terá os valores dos componentes principais para todas as 569 amostras.
principal_breast_Df = pd.DataFrame(data = principalComponents_breast
, columns = ['principal component 1', 'principal component 2'])
principal_breast_Df.tail()
| componente principal 1 | componente principal 2 | |
|---|---|---|
| 564 | 6.439315 | -3.576817 |
| 565 | 3.793382 | -3.584048 |
| 566 | 1.256179 | -1.902297 |
| 567 | 10.374794 | 1.672010 |
| 568 | -5.475243 | -0.670637 |
- Depois de obter os componentes principais, você pode encontrar o
explained_variance_ratio. Ele fornecerá a você a quantidade de informações ou a variação que cada componente principal possui após a projeção dos dados em um subespaço de dimensão inferior.
print('Explained variability per principal component: {}'.format(pca_breast.explained_variance_ratio_))
Explained variability per principal component: [0.44272026 0.18971182]
Na saída acima, você pode observar que o principal component 1 contém 44,2% das informações, enquanto o principal component 2 contém apenas 19% das informações. Além disso, outro ponto a ser observado é que, ao projetar dados tridimensionais em dados bidimensionais, 36,8% das informações foram perdidas.
Vamos traçar a visualização das 569 amostras ao longo dos eixos principal component - 1 e principal component - 2. Isso deve dar a você uma boa visão de como suas amostras estão distribuídas entre as duas classes.
plt.figure()
plt.figure(figsize=(10,10))
plt.xticks(fontsize=12)
plt.yticks(fontsize=14)
plt.xlabel('Principal Component - 1',fontsize=20)
plt.ylabel('Principal Component - 2',fontsize=20)
plt.title("Principal Component Analysis of Breast Cancer Dataset",fontsize=20)
targets = ['Benign', 'Malignant']
colors = ['r', 'g']
for target, color in zip(targets,colors):
indicesToKeep = breast_dataset['label'] == target
plt.scatter(principal_breast_Df.loc[indicesToKeep, 'principal component 1']
, principal_breast_Df.loc[indicesToKeep, 'principal component 2'], c = color, s = 50)
plt.legend(targets,prop={'size': 15})
<matplotlib.legend.Legend at 0x14552a630>
<Figure size 432x288 with 0 Axes>
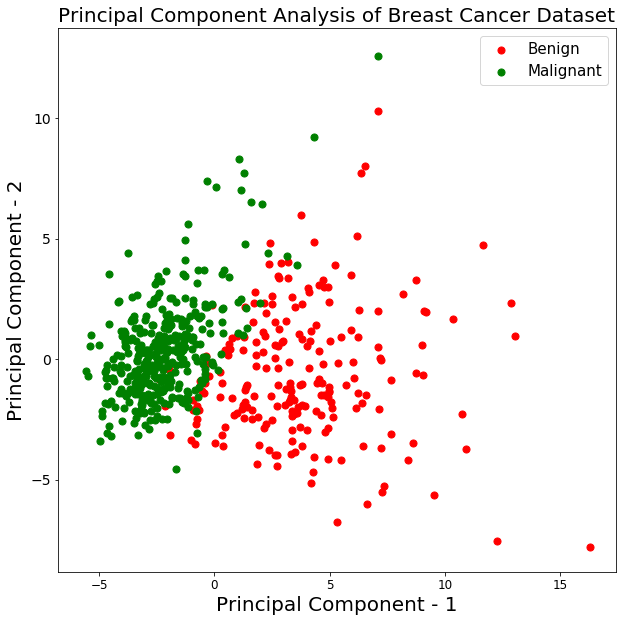
No gráfico acima, você pode observar que as duas classes benign e malignant, quando projetadas em um espaço bidimensional, podem ser linearmente separáveis até certo ponto. Outras observações podem ser que a classe benign está espalhada em comparação com a classe malignant.
Visualização dos dados do CIFAR - 10
As seguintes linhas de código para visualizar os dados do CIFAR-10 são muito semelhantes à visualização PCA dos dados do câncer de mama.
- Vamos verificar rapidamente os valores máximo e mínimo das imagens de treinamento CIFAR-10 e
normalizeos pixels entre 0 e 1, inclusive.
np.min(x_train),np.max(x_train)
(0.0, 1.0)
x_train = x_train/255.0
np.min(x_train),np.max(x_train)
(0.0, 0.00392156862745098)
x_train.shape
(50000, 32, 32, 3)
Em seguida, você criará um DataFrame que conterá os valores de pixel das imagens junto com seus respectivos rótulos em um formato de linha-coluna.
Mas antes disso, vamos remodelar as dimensões da imagem de três para uma (achatar as imagens).
x_train_flat = x_train.reshape(-1,3072)
feat_cols = ['pixel'+str(i) for i in range(x_train_flat.shape[1])]
df_cifar = pd.DataFrame(x_train_flat,columns=feat_cols)
df_cifar['label'] = y_train
print('Size of the dataframe: {}'.format(df_cifar.shape))
Size of the dataframe: (50000, 3073)
Perfeito! O tamanho do dataframe está correto, pois há 50.000 imagens de treinamento, cada uma com 3.072 pixels e uma coluna adicional para rótulos, totalizando 3.073.
A PCA será aplicada em todas as colunas, exceto na última, que é o rótulo de cada imagem.
df_cifar.head()
| pixel0 | pixel1 | pixel2 | pixel3 | pixel4 | pixel5 | pixel6 | pixel7 | pixel8 | pixel9 | ... | pixel3063 | pixel3064 | pixel3065 | pixel3066 | pixel3067 | pixel3068 | pixel3069 | pixel3070 | pixel3071 | rótulo | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.231373 | 0.243137 | 0.247059 | 0.168627 | 0.180392 | 0.176471 | 0.196078 | 0.188235 | 0.168627 | 0.266667 | ... | 0.847059 | 0.721569 | 0.549020 | 0.592157 | 0.462745 | 0.329412 | 0.482353 | 0.360784 | 0.282353 | 6 |
| 1 | 0.603922 | 0.694118 | 0.733333 | 0.494118 | 0.537255 | 0.533333 | 0.411765 | 0.407843 | 0.372549 | 0.400000 | ... | 0.560784 | 0.521569 | 0.545098 | 0.560784 | 0.525490 | 0.556863 | 0.560784 | 0.521569 | 0.564706 | 9 |
| 2 | 1.000000 | 1.000000 | 1.000000 | 0.992157 | 0.992157 | 0.992157 | 0.992157 | 0.992157 | 0.992157 | 0.992157 | ... | 0.305882 | 0.333333 | 0.325490 | 0.309804 | 0.333333 | 0.325490 | 0.313725 | 0.337255 | 0.329412 | 9 |
| 3 | 0.109804 | 0.098039 | 0.039216 | 0.145098 | 0.133333 | 0.074510 | 0.149020 | 0.137255 | 0.078431 | 0.164706 | ... | 0.211765 | 0.184314 | 0.109804 | 0.247059 | 0.219608 | 0.145098 | 0.282353 | 0.254902 | 0.180392 | 4 |
| 4 | 0.666667 | 0.705882 | 0.776471 | 0.658824 | 0.698039 | 0.768627 | 0.694118 | 0.725490 | 0.796078 | 0.717647 | ... | 0.294118 | 0.309804 | 0.321569 | 0.278431 | 0.294118 | 0.305882 | 0.286275 | 0.301961 | 0.313725 | 1 |
5 linhas × 3073 colunas
- Em seguida, você criará o método PCA, passará o número de componentes como dois e aplicará
fit_transformnos dados de treinamento, o que pode levar alguns segundos, pois há 50.000 amostras
pca_cifar = PCA(n_components=2)
principalComponents_cifar = pca_cifar.fit_transform(df_cifar.iloc[:,:-1])
Em seguida, você converterá os componentes principais de cada uma das 50.000 imagens de uma matriz numpy para um DataFrame do pandas.
principal_cifar_Df = pd.DataFrame(data = principalComponents_cifar
, columns = ['principal component 1', 'principal component 2'])
principal_cifar_Df['y'] = y_train
principal_cifar_Df.head()
| componente principal 1 | componente principal 2 | y | |
|---|---|---|---|
| 0 | -6.401018 | 2.729039 | 6 |
| 1 | 0.829783 | -0.949943 | 9 |
| 2 | 7.730200 | -11.522102 | 9 |
| 3 | -10.347817 | 0.010738 | 4 |
| 4 | -2.625651 | -4.969240 | 1 |
- Vamos descobrir rapidamente a quantidade de informações ou
varianceos componentes principais que você possui.
print('Explained variability per principal component: {}'.format(pca_cifar.explained_variance_ratio_))
Explained variability per principal component: [0.2907663 0.11253144]
Bem, parece que uma quantidade razoável de informações foi retida pelos componentes principais 1 e 2, já que os dados foram projetados de 3.072 dimensões para apenas dois componentes principais.
É hora de visualizar os dados do CIFAR-10 em um espaço bidimensional. Lembre-se de que há alguma sobreposição de classe semântica nesse conjunto de dados, o que significa que um sapo pode ter uma forma ligeiramente semelhante à de um gato ou de um cervo com um cachorro, especialmente quando projetado em um espaço bidimensional. As diferenças entre eles podem não ser capturadas tão bem.
import seaborn as sns
plt.figure(figsize=(16,10))
sns.scatterplot(
x="principal component 1", y="principal component 2",
hue="y",
palette=sns.color_palette("hls", 10),
data=principal_cifar_Df,
legend="full",
alpha=0.3
)
<matplotlib.axes._subplots.AxesSubplot at 0x12a5ba8d0>
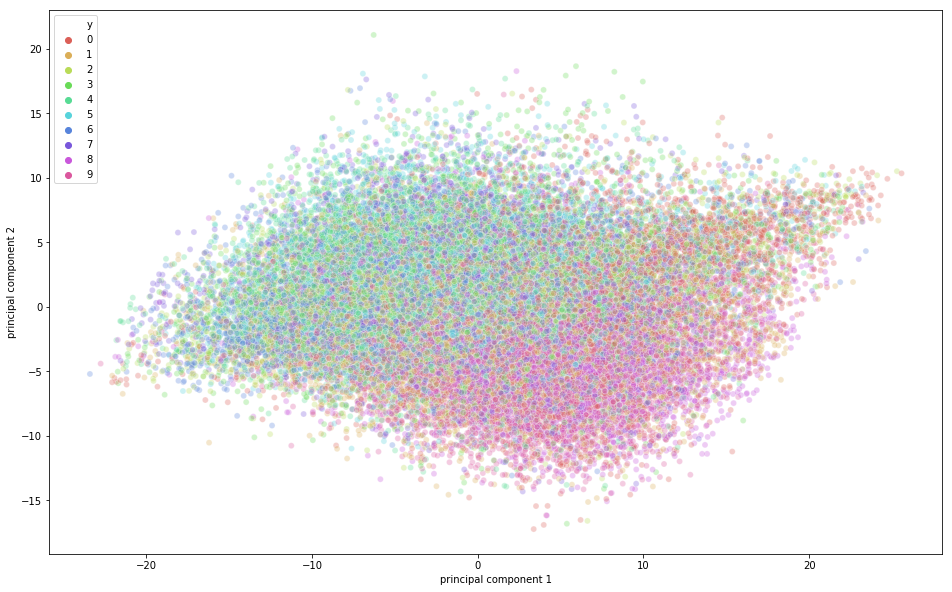
Na figura acima, você pode observar que alguma variação foi capturada pelos componentes principais, pois há alguma estrutura nos pontos quando projetados ao longo dos dois eixos de componentes principais. Os pontos que pertencem à mesma classe estão próximos uns dos outros, e os pontos ou imagens que são muito diferentes semanticamente estão mais distantes uns dos outros.
Acelerar o treinamento de aprendizagem profunda usando PCA
Neste segmento final do tutorial, você aprenderá como acelerar o processo de treinamento do seu modelo de aprendizagem profunda usando PCA.
Observação: Para aprender as terminologias básicas que serão usadas nesta seção, consulte este tutorial.
Primeiro, vamos normalizar as imagens de treinamento e teste. Se você se lembrar, as imagens de treinamento foram normalizadas na parte de visualização do PCA, portanto, você só precisa normalizar as imagens de teste. Então, vamos fazer isso rapidamente!
x_test = x_test/255.0
x_test = x_test.reshape(-1,32,32,3)
Vamos acessar reshape os dados de teste.
x_test_flat = x_test.reshape(-1,3072)
Em seguida, você criará a instância do modelo PCA.
Aqui, você também pode passar a quantidade de variação que deseja que a PCA capture. Vamos passar 0,9 como um parâmetro para o modelo PCA, o que significa que o PCA reterá 90% da variação e o number of components necessário para capturar 90% da variação será usado.
Observe que, anteriormente, você passou o endereço n_components como parâmetro e pôde descobrir a variação capturada por esses dois componentes. Mas aqui mencionamos explicitamente a variação que gostaríamos que o PCA capturasse e, portanto, o n_components variará com base no parâmetro de variação.
Se você não passar nenhuma variância, o número de componentes será igual à dimensão original dos dados.
pca = PCA(0.9)
Em seguida, você ajustará a instância PCA nas imagens de treinamento.
pca.fit(x_train_flat)
PCA(copy=True, iterated_power='auto', n_components=0.9, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
Agora vamos descobrir quantos n_components PCA usou para capturar a variação de 0,9.
pca.n_components_
99
Na saída acima, você pode observar que, para obter 90% de variação, a dimensão foi reduzida para 99 componentes principais das 3072 dimensões reais.
Por fim, você aplicará o transform no conjunto de treinamento e teste para gerar um conjunto de dados transformado a partir dos parâmetros gerados pelo método fit.
train_img_pca = pca.transform(x_train_flat)
test_img_pca = pca.transform(x_test_flat)
Em seguida, vamos importar rapidamente as bibliotecas necessárias para executar o modelo de aprendizagem profunda.
from keras.models import Sequential
from keras.layers import Dense
from keras.utils import np_utils
from keras.optimizers import RMSprop
Agora, você converterá seus rótulos de treinamento e teste em um vetor de codificação de um único disparo.
y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
Vamos definir o número de épocas, o número de classes e o tamanho do lote para seu modelo.
batch_size = 128
num_classes = 10
epochs = 20
Em seguida, você definirá seu modelo Sequential!
model = Sequential()
model.add(Dense(1024, activation='relu', input_shape=(99,)))
model.add(Dense(1024, activation='relu'))
model.add(Dense(512, activation='relu'))
model.add(Dense(256, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
Vamos imprimir o resumo do modelo.
model.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 1024) 102400
_________________________________________________________________
dense_2 (Dense) (None, 1024) 1049600
_________________________________________________________________
dense_3 (Dense) (None, 512) 524800
_________________________________________________________________
dense_4 (Dense) (None, 256) 131328
_________________________________________________________________
dense_5 (Dense) (None, 10) 2570
=================================================================
Total params: 1,810,698
Trainable params: 1,810,698
Non-trainable params: 0
_________________________________________________________________
Finalmente, é hora de compilar e treinar o modelo!
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
history = model.fit(train_img_pca, y_train,batch_size=batch_size,epochs=epochs,verbose=1,
validation_data=(test_img_pca, y_test))
WARNING:tensorflow:From /Users/adityasharma/blog/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:2704: calling reduce_sum (from tensorflow.python.ops.math_ops) with keep_dims is deprecated and will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead
WARNING:tensorflow:From /Users/adityasharma/blog/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:1257: calling reduce_mean (from tensorflow.python.ops.math_ops) with keep_dims is deprecated and will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead
Train on 50000 samples, validate on 10000 samples
Epoch 1/20
50000/50000 [==============================] - 7s - loss: 1.9032 - acc: 0.2962 - val_loss: 1.6925 - val_acc: 0.3875
Epoch 2/20
50000/50000 [==============================] - 7s - loss: 1.6480 - acc: 0.4055 - val_loss: 1.5313 - val_acc: 0.4412
Epoch 3/20
50000/50000 [==============================] - 7s - loss: 1.5205 - acc: 0.4534 - val_loss: 1.4609 - val_acc: 0.4695
Epoch 4/20
50000/50000 [==============================] - 7s - loss: 1.4322 - acc: 0.4849 - val_loss: 1.6164 - val_acc: 0.4503
Epoch 5/20
50000/50000 [==============================] - 7s - loss: 1.3621 - acc: 0.5120 - val_loss: 1.3626 - val_acc: 0.5081
Epoch 6/20
50000/50000 [==============================] - 7s - loss: 1.2995 - acc: 0.5330 - val_loss: 1.4100 - val_acc: 0.4940
Epoch 7/20
50000/50000 [==============================] - 7s - loss: 1.2473 - acc: 0.5529 - val_loss: 1.3589 - val_acc: 0.5251
Epoch 8/20
50000/50000 [==============================] - 7s - loss: 1.2010 - acc: 0.5669 - val_loss: 1.3315 - val_acc: 0.5232
Epoch 9/20
50000/50000 [==============================] - 7s - loss: 1.1524 - acc: 0.5868 - val_loss: 1.3903 - val_acc: 0.5197
Epoch 10/20
50000/50000 [==============================] - 7s - loss: 1.1134 - acc: 0.6013 - val_loss: 1.2722 - val_acc: 0.5499
Epoch 11/20
50000/50000 [==============================] - 7s - loss: 1.0691 - acc: 0.6160 - val_loss: 1.5911 - val_acc: 0.4768
Epoch 12/20
50000/50000 [==============================] - 7s - loss: 1.0325 - acc: 0.6289 - val_loss: 1.2515 - val_acc: 0.5602
Epoch 13/20
50000/50000 [==============================] - 7s - loss: 0.9977 - acc: 0.6420 - val_loss: 1.5678 - val_acc: 0.4914
Epoch 14/20
50000/50000 [==============================] - 8s - loss: 0.9567 - acc: 0.6567 - val_loss: 1.3525 - val_acc: 0.5418
Epoch 15/20
50000/50000 [==============================] - 9s - loss: 0.9158 - acc: 0.6713 - val_loss: 1.3525 - val_acc: 0.5540
Epoch 16/20
50000/50000 [==============================] - 10s - loss: 0.8948 - acc: 0.6816 - val_loss: 1.5633 - val_acc: 0.5156
Epoch 17/20
50000/50000 [==============================] - 9s - loss: 0.8690 - acc: 0.6903 - val_loss: 1.6980 - val_acc: 0.5084
Epoch 18/20
50000/50000 [==============================] - 9s - loss: 0.8586 - acc: 0.7002 - val_loss: 1.6325 - val_acc: 0.5247
Epoch 19/20
50000/50000 [==============================] - 8s - loss: 0.9367 - acc: 0.6853 - val_loss: 1.8253 - val_acc: 0.5165
Epoch 20/20
50000/50000 [==============================] - 8s - loss: 2.3761 - acc: 0.5971 - val_loss: 6.0192 - val_acc: 0.4409
Na saída acima, você pode observar que o tempo necessário para treinar cada época foi de apenas 7 seconds em uma CPU. O modelo fez um trabalho decente nos dados de treinamento, alcançando uma precisão de 70%, enquanto obteve apenas uma precisão de 56% nos dados de teste. Isso significa que você ajustou demais os dados de treinamento. No entanto, lembre-se de que os dados foram projetados em 99 dimensões a partir de 3.072 dimensões e, apesar disso, ele fez um ótimo trabalho!
Por fim, vamos ver quanto tempo o modelo leva para ser treinado no conjunto de dados original e quanta precisão ele pode alcançar usando o mesmo modelo de aprendizagem profunda.
model = Sequential()
model.add(Dense(1024, activation='relu', input_shape=(3072,)))
model.add(Dense(1024, activation='relu'))
model.add(Dense(512, activation='relu'))
model.add(Dense(256, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
history = model.fit(x_train_flat, y_train,batch_size=batch_size,epochs=epochs,verbose=1,
validation_data=(x_test_flat, y_test))
Train on 50000 samples, validate on 10000 samples
Epoch 1/20
50000/50000 [==============================] - 23s - loss: 2.0657 - acc: 0.2200 - val_loss: 2.0277 - val_acc: 0.2485
Epoch 2/20
50000/50000 [==============================] - 22s - loss: 1.8727 - acc: 0.3166 - val_loss: 1.8428 - val_acc: 0.3215
Epoch 3/20
50000/50000 [==============================] - 22s - loss: 1.7801 - acc: 0.3526 - val_loss: 1.7657 - val_acc: 0.3605
Epoch 4/20
50000/50000 [==============================] - 22s - loss: 1.7141 - acc: 0.3796 - val_loss: 1.6345 - val_acc: 0.4132
Epoch 5/20
50000/50000 [==============================] - 22s - loss: 1.6566 - acc: 0.4001 - val_loss: 1.6384 - val_acc: 0.4076
Epoch 6/20
50000/50000 [==============================] - 22s - loss: 1.6083 - acc: 0.4209 - val_loss: 1.7507 - val_acc: 0.3574
Epoch 7/20
50000/50000 [==============================] - 22s - loss: 1.5626 - acc: 0.4374 - val_loss: 1.7125 - val_acc: 0.4010
Epoch 8/20
50000/50000 [==============================] - 22s - loss: 1.5252 - acc: 0.4486 - val_loss: 1.5914 - val_acc: 0.4321
Epoch 9/20
50000/50000 [==============================] - 24s - loss: 1.4924 - acc: 0.4620 - val_loss: 1.5352 - val_acc: 0.4616
Epoch 10/20
50000/50000 [==============================] - 25s - loss: 1.4627 - acc: 0.4728 - val_loss: 1.4561 - val_acc: 0.4798
Epoch 11/20
50000/50000 [==============================] - 24s - loss: 1.4349 - acc: 0.4820 - val_loss: 1.5044 - val_acc: 0.4723
Epoch 12/20
50000/50000 [==============================] - 24s - loss: 1.4120 - acc: 0.4919 - val_loss: 1.4740 - val_acc: 0.4790
Epoch 13/20
50000/50000 [==============================] - 23s - loss: 1.3913 - acc: 0.4981 - val_loss: 1.4430 - val_acc: 0.4891
Epoch 14/20
50000/50000 [==============================] - 27s - loss: 1.3678 - acc: 0.5098 - val_loss: 1.4323 - val_acc: 0.4888
Epoch 15/20
50000/50000 [==============================] - 27s - loss: 1.3508 - acc: 0.5148 - val_loss: 1.6179 - val_acc: 0.4372
Epoch 16/20
50000/50000 [==============================] - 25s - loss: 1.3443 - acc: 0.5167 - val_loss: 1.5868 - val_acc: 0.4656
Epoch 17/20
50000/50000 [==============================] - 25s - loss: 1.3734 - acc: 0.5101 - val_loss: 1.4756 - val_acc: 0.4913
Epoch 18/20
50000/50000 [==============================] - 26s - loss: 5.5126 - acc: 0.3591 - val_loss: 5.7580 - val_acc: 0.3084
Epoch 19/20
50000/50000 [==============================] - 27s - loss: 5.6346 - acc: 0.3395 - val_loss: 3.7362 - val_acc: 0.3402
Epoch 20/20
50000/50000 [==============================] - 26s - loss: 6.4199 - acc: 0.3030 - val_loss: 13.9429 - val_acc: 0.1326
Voila! A partir do resultado acima, fica evidente que o tempo necessário para treinar cada época foi de cerca de 23 seconds em uma CPU, o que foi quase três vezes mais do que o modelo treinado na saída do PCA.
Além disso, tanto a precisão do treinamento quanto do teste é menor do que a precisão que você obteve com os 99 componentes principais como entrada para o modelo.
Portanto, ao aplicar o PCA nos dados de treinamento, você conseguiu treinar seu algoritmo de aprendizagem profunda não apenas fast, mas também obteve um melhor accuracy nos dados de teste quando comparado com o algoritmo de aprendizagem profunda treinado com os dados de treinamento originais.
Vá além!
Parabéns por você ter concluído o tutorial.
Esse tutorial foi uma introdução excelente e abrangente ao PCA em Python, que cobriu tanto os conceitos teóricos quanto os práticos do PCA.
Se você quiser se aprofundar nas técnicas de redução de dimensionalidade, considere ler sobre o t-distributed Stochastic Neighbor Embedding, comumente conhecido como tSNE, que é uma técnica de redução de dimensionalidade probabilística não linear.
Se você quiser saber mais sobre técnicas de aprendizagem não supervisionada, como PCA, faça o curso Aprendizagem não supervisionada em Python do DataCamp.
Referências para você aprender mais:
Perguntas frequentes
Qual é a diferença entre a análise de fatores e a análise de componentes principais?
A análise de fatores (FA) e a análise de componentes principais (PCA) são técnicas usadas para reduzir a dimensionalidade, mas têm objetivos diferentes. A ACP concentra-se em preservar a variabilidade total dos dados, transformando-os em um novo conjunto de variáveis não correlacionadas (componentes principais), ordenadas pela quantidade de variação que explicam. Em contrapartida, a AF visa identificar as relações subjacentes entre as variáveis observadas, modelando os dados com alguns fatores latentes que explicam as correlações entre as variáveis.
