Comment calculer le coefficient de variation dans Excel ?

En tant que scientifiques des données, il est essentiel de comprendre la variabilité de nos données. Le coefficient de variation (CV) est une mesure utile qui exprime cette variabilité en proportion de la moyenne, ce qui permet de comparer des ensembles de données ayant des unités différentes.

Dans ce tutoriel, nous allons découvrir le coefficient de variation en tant que concept statistique et comment trouver le coefficient de variation dans Excel.

Si vous êtes à la recherche d'une introduction complète à Excel, consultez ce cursus de cinq cours sur les fondamentaux d'Excel.

Examinons d'abord une réponse très courte, puis ajoutons des détails.

Réponse courte : Comment calculer le coefficient de variation dans Excel ?

Voici la procédure étape par étape pour trouver le coefficient de variation dans Excel :

• Calculez l'écart-type: Dans une cellule vide, nous entrons la formule =STDEV.P(A1:A10), en remplaçant A1:A10 par la plage réelle de nos données.
• Calculez la moyenne: Dans une autre cellule vide, nous entrons la formule =AVERAGE(A1:A10) en utilisant la même plage de données.
• Calculez le coefficient de variation: Dans une dernière cellule, nous entrons la formule =STDEV.P(A1:A10)/AVERAGE(A1:A10). L'écart-type est divisé par la moyenne.

Qu'est-ce que le coefficient de variation ?

Le coefficient de variation (CV) est une mesure statistique qui quantifie la variabilité relative d'un ensemble de données par rapport à sa moyenne.

Nous l'exprimons généralement sous forme de pourcentage et le calculons en divisant l'écart-type de l'ensemble de données par la moyenne, puis en multipliant le résultat par 100.

La formule pour calculer le coefficient de variation est la suivante :

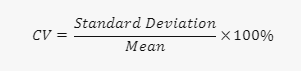
Le CV nous permet de comparer la variabilité de deux ou plusieurs ensembles de données qui peuvent avoir des unités ou des moyennes différentes, en fournissant une mesure standardisée de la dispersion.

Un CV plus faible indique que les points de données sont plus proches de la moyenne, ce qui reflète une plus faible variabilité. Inversement, un CV plus élevé suggère une plus grande dispersion des points de données autour de la moyenne.

La force du CV réside dans la comparaison de la variabilité entre des ensembles de données ayant des unités différentes. Elle est donc particulièrement utile dans des domaines tels que la finance, où elle permet d'évaluer le rapport risque/récompense de différents portefeuilles d'investissement.

De même, dans le cadre du contrôle de la qualité, le CV peut aider à comparer la cohérence des processus de production qui utilisent des échelles de mesure différentes.

Examinons plus en détail les applications du monde réel.

Applications du coefficient de variation

Dans le domaine de la finance et de l'évaluation des risques, les investisseurs utilisent le CV pour identifier les actifs qui offrent des rendements plus élevés par rapport à leur risque inhérent. Cela leur permet de construire des portefeuilles diversifiés et de gérer efficacement les risques. Cette application est particulièrement utile sur les marchés où les rendements absolus peuvent être trompeurs en raison de niveaux de volatilité variables.

Le CV joue également un rôle important dans le contrôle de la qualité de la fabrication. Il permet de garantir une qualité constante des produits dans les différents lots de production. Un CV plus faible indique une moindre variation des caractéristiques du produit, ce qui est essentiel pour maintenir les normes de la marque et la satisfaction du client.

Les industries telles que l'industrie pharmaceutique et l'industrie automobile, où la fiabilité des produits est primordiale, s'appuient fortement sur la CV pour évaluer et contrôler les processus de production.

Les chercheurs et les météorologues l'utilisent pour analyser la cohérence des modèles météorologiques, tels que les variations de précipitations dans différentes régions ou périodes. Cette analyse permet d'améliorer la précision des prévisions météorologiques et de planifier les activités agricoles qui dépendent fortement des conditions météorologiques.

N'oubliez pas que le CV est une mesure relative de la dispersion. Sa force réside dans la comparaison de la variabilité entre plusieurs ensembles de données ou variables. Elle est moins informative lorsqu'elle est utilisée pour décrire la variabilité d'un seul ensemble de données pris isolément. Les applications du CV vont au-delà de ces exemples et en font un outil précieux dans de nombreux secteurs d'activité.

Voyons maintenant comment calculer le coefficient de variation dans Excel à l'aide d'un exemple.

Comment trouver le coefficient de variation dans Excel ?

Contrairement à d'autres calculs dans Excel, nous ne disposons pas d'une fonction d'une ligne pour calculer le CV. Cependant, le processus est encore simple, comme nous le verrons bientôt.

Imaginez que vous êtes un analyste de données financières chargé d'évaluer des portefeuilles d'investissement pour l'équipe de gestion des actifs d'une entreprise. Pour guider leurs décisions stratégiques, vous devez évaluer le risque associé à chaque portefeuille. Le CV est très utile à cet égard.

En comparant l'écart-type des rendements de chaque portefeuille au rendement moyen, vous pouvez déterminer leur profil risque-rendement. Cette mesure peut montrer quels portefeuilles offrent des rendements plus élevés par rapport au niveau de risque encouru.

Pour calculer le coefficient de variation de chaque portefeuille, commençons par tabuler les rendements de chaque portefeuille pour chaque mois de l'année :

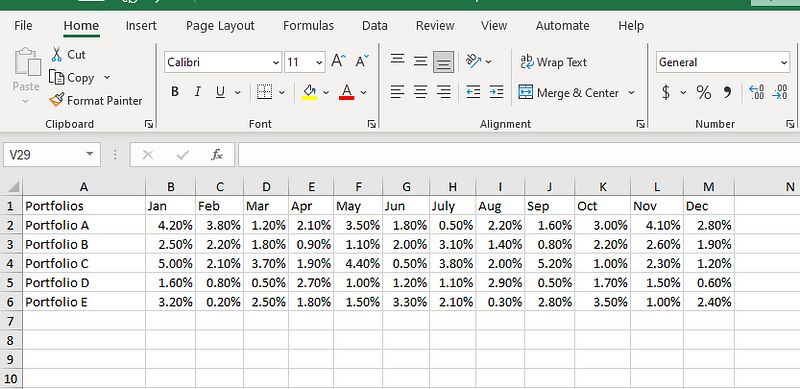
Données sur les rendements des portefeuilles.

Nous calculerons la moyenne pour chaque portefeuille (rappelez-vous que la formule du CV exige que nous connaissions la moyenne). Saisissons la formule ci-dessous dans la cellule N2:

=AVERAGE(B2:M2)

Calcul de la moyenne dans Excel.

Nous faisons maintenant glisser la poignée de remplissage (le petit carré dans le coin inférieur droit de N2) pour étendre la formule aux autres portefeuilles.

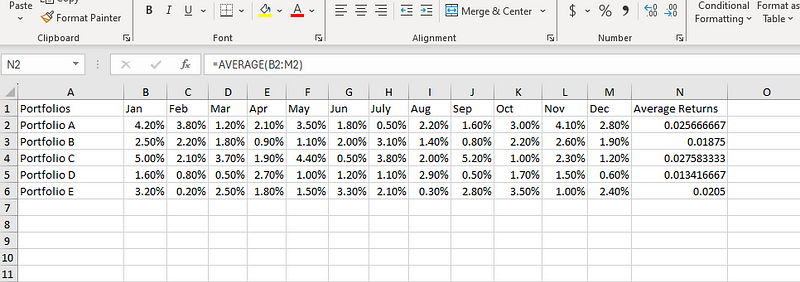
Extension de la moyenne calculée à d'autres portefeuilles.

Nous avons la moyenne, mais nous avons besoin d'un autre élément pour notre formule de CV : l'écart-type. Sélectionnons O2 et utilisons la formule suivante pour calculer l'écart-type :

=STDEV.P(B2:M2)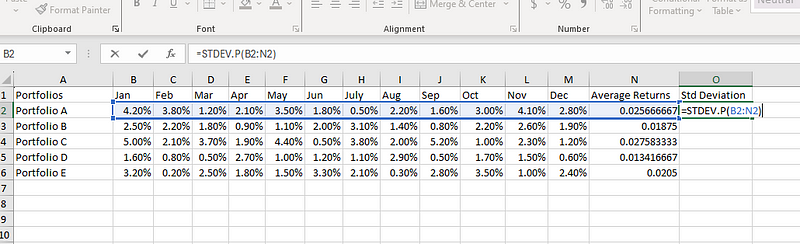

Calcul de l'écart-type dans Excel.

Nous faisons maintenant glisser la poignée de remplissage pour étendre la formule aux autres portefeuilles. Par ailleurs, nous avons utilisé STDEV.P() au lieu de STDEV.S() parce que, dans notre exemple, nous supposons que notre ensemble de données est une population et non un échantillon.

Maintenant que nous disposons de la moyenne et de l'écart-type, nous pouvons calculer le CV. Divisons l'écart-type par la moyenne dans P2:

=N2/O2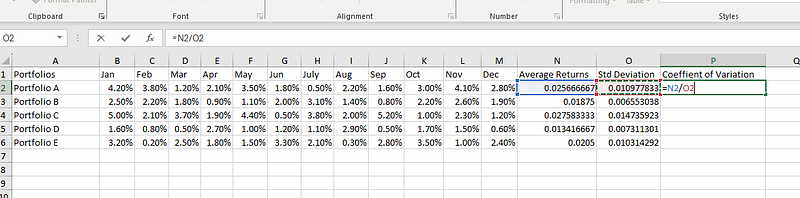

Calcul du coefficient de variation dans Excel.

Comme précédemment, nous faisons glisser la poignée de remplissage pour étendre la formule aux autres portefeuilles.

Comme le CV est généralement exprimé en pourcentage, nous sélectionnons P2 à P6, et nous changeons le formatage des nombres en pourcentage, comme le montre le diagramme ci-dessous.

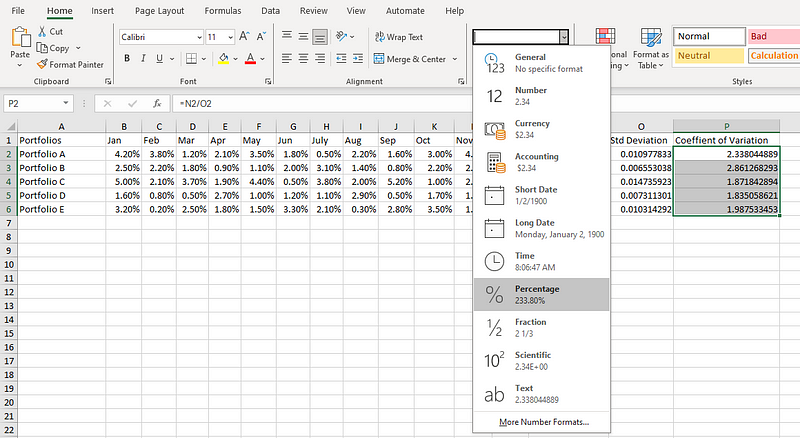
Transformer les valeurs en pourcentages.

Et voilà, toutes nos valeurs de CV se trouvent dans la colonne P!

Données finales avec tous les calculs.