Cómo calcular el Coeficiente de Variación en Excel

Como científicos de datos, es crucial comprender la variabilidad de nuestros datos. El coeficiente de variación (CV) es una métrica útil que expresa esta variabilidad como proporción de la media, lo que permite hacer comparaciones entre conjuntos de datos con unidades diferentes.

En este tutorial, aprenderemos sobre el coeficiente de variación como concepto estadístico y cómo hallar el coeficiente de variación en Excel.

Si buscas una introducción completa a Excel, echa un vistazo a este curso de cinco cursos de Fundamentos de Excel.

Veamos primero una respuesta muy breve y luego añadiremos más detalles.

Respuesta corta: Cómo calcular el Coeficiente de Variación en Excel

Aquí tienes el proceso paso a paso para hallar el coeficiente de variación en Excel:

• Calcula la desviación típica: En una celda vacía, introducimos la fórmula =STDEV.P(A1:A10), sustituyendo A1:A10 por el rango real de nuestros datos.
• Calcula la media: En otra celda vacía, introducimos la fórmula =AVERAGE(A1:A10) utilizando el mismo rango de datos.
• Calcula el coeficiente de variación: En una última celda, introducimos la fórmula =STDEV.P(A1:A10)/AVERAGE(A1:A10). Divide la desviación típica por la media.

¿Qué es el Coeficiente de Variación?

El coeficiente de variación (CV) es una medida estadística que cuantifica la variabilidad relativa de un conjunto de datos respecto a su media.

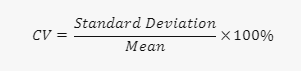
Normalmente la expresamos en porcentaje y la calculamos dividiendo la desviación típica del conjunto de datos por la media y multiplicando el resultado por 100.

La fórmula para calcular el coeficiente de variación es

El CV nos permite comparar la variabilidad de dos o más conjuntos de datos que pueden tener unidades o medias diferentes, proporcionando una medida normalizada de la dispersión.

Un CV más bajo indica que los puntos de datos están agrupados más cerca de la media, lo que refleja una menor variabilidad. A la inversa, un CV más alto sugiere una mayor dispersión de los puntos de datos en torno a la media.

La fuerza del CV reside en comparar la variabilidad entre conjuntos de datos con unidades diferentes. Esto lo hace especialmente útil en áreas como las finanzas, donde puede evaluar la relación riesgo-recompensa de distintas carteras de inversión.

Del mismo modo, en el control de calidad, el CV puede ayudar a comparar la coherencia de los procesos de producción que utilizan diferentes escalas de medición.

Profundicemos en las aplicaciones en el mundo real.

Aplicaciones del Coeficiente de Variación

En finanzas y evaluación de riesgos, los inversores utilizan la CV para identificar los activos que ofrecen mayores rendimientos en relación con su riesgo inherente. Esto les permite crear carteras diversificadas y gestionar el riesgo con eficacia. Esta aplicación es especialmente útil en mercados en los que los rendimientos absolutos pueden ser engañosos debido a la variación de los niveles de volatilidad.

El CV también desempeña un papel importante en el control de calidad de la fabricación. Ayuda a garantizar una calidad constante del producto en los distintos lotes de producción. Un CV más bajo indica menos variación en las características del producto, lo que es crucial para mantener los estándares de la marca y la satisfacción del cliente.

Industrias como la farmacéutica y la automovilística, donde la fiabilidad del producto es primordial, dependen mucho de la CV para evaluar y controlar los procesos de producción.

Los investigadores y meteorólogos lo utilizan para analizar la coherencia de los patrones meteorológicos, como las variaciones de las precipitaciones en distintas regiones o periodos de tiempo. Este análisis ayuda a mejorar la precisión de las previsiones meteorológicas y a planificar las actividades agrícolas que dependen en gran medida de las condiciones meteorológicas.

Recuerda que el CV es una medida relativa de dispersión. Su fuerza reside en comparar la variabilidad entre múltiples conjuntos de datos o variables. Es menos informativo cuando se utiliza para describir la variabilidad de un único conjunto de datos de forma aislada. Las aplicaciones del CV van más allá de estos ejemplos, por lo que es una herramienta valiosa en muchos sectores.

Ahora vamos a aprender a calcular el coeficiente de variación en Excel mediante un ejemplo.

Cómo hallar el coeficiente de variación en Excel

A diferencia de otros cálculos en Excel, no tenemos una función de una línea para calcular el CV. Sin embargo, el proceso sigue siendo sencillo, como veremos en breve.

Imagina que eres un analista de datos financieros encargado de evaluar carteras de inversión para el equipo de gestión de activos de una empresa. Para orientar sus decisiones estratégicas, tienes que evaluar el riesgo asociado a cada cartera. El CV es muy útil en este caso.

Comparando la desviación típica de los rendimientos de cada cartera con el rendimiento medio, puedes determinar sus perfiles de riesgo-rentabilidad. Esta medida puede mostrar qué carteras ofrecen mayores rendimientos en relación con el nivel de riesgo que entrañan.

Para calcular el coeficiente de variación de cada cartera, empecemos por tabular los rendimientos de cada cartera para cada mes del año:

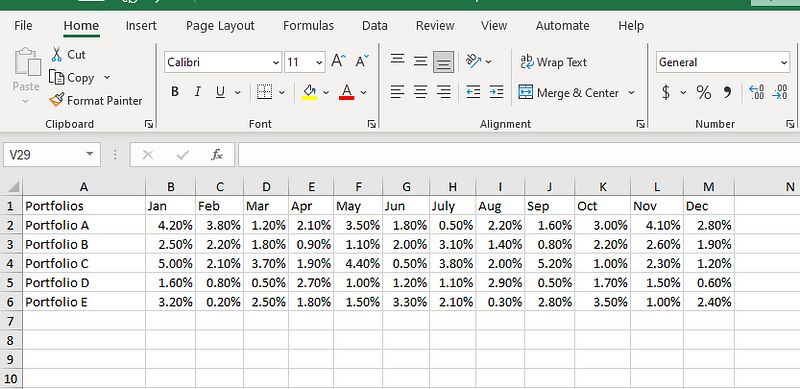
Datos de rentabilidad de la cartera.

Calcularemos la media de cada cartera (recuerda que la fórmula del CV requiere que conozcamos la media). Escribamos la fórmula siguiente en la celda N2:

=AVERAGE(B2:M2)

Calcular la media en Excel.

Ahora, arrastramos el tirador de relleno (el pequeño cuadrado de la esquina inferior derecha de N2) para extender la fórmula a las demás carteras.

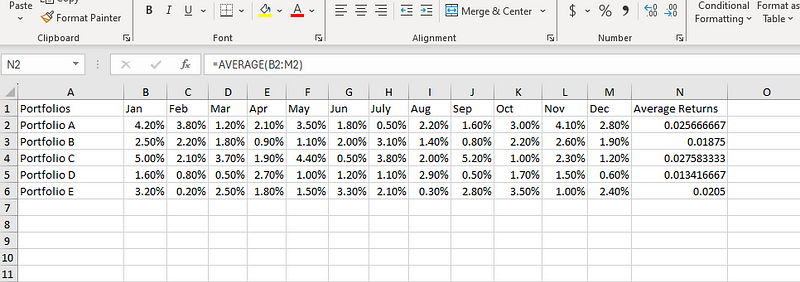
Extender la media calculada a otras carteras.

Tenemos la media, pero necesitamos otro elemento para nuestra fórmula de CV: la desviación típica. Seleccionemos O2 y utilicemos la siguiente fórmula para calcular la desviación típica:

=STDEV.P(B2:M2)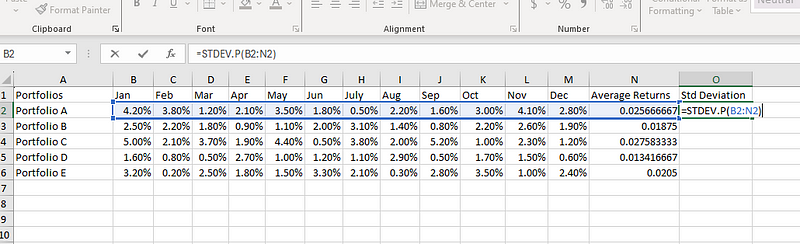

Calcular la desviación típica en Excel.

Ahora arrastramos el tirador de relleno para extender la fórmula a las demás carteras. Como nota al margen, hemos utilizado STDEV.P() en lugar de STDEV.S() porque en nuestro ejemplo suponemos que nuestro conjunto de datos es una población en lugar de una muestra.

Ahora que tenemos la media y la desviación típica, podemos calcular el CV. Dividamos la desviación típica por la media en P2:

=N2/O2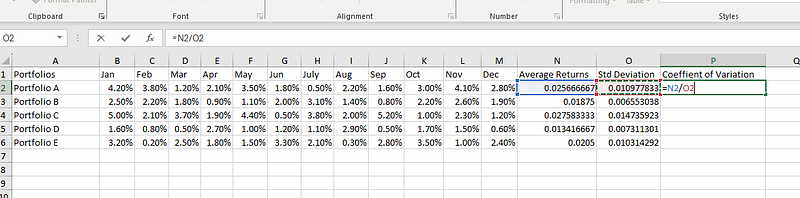

Calcular el coeficiente de variación en Excel.

Como antes, arrastramos el tirador de relleno para extender la fórmula al resto de carteras.

Como el CV suele expresarse en porcentaje, seleccionamos P2 a P6, y cambiamos el formato numérico a Porcentaje, como se muestra en el diagrama siguiente.

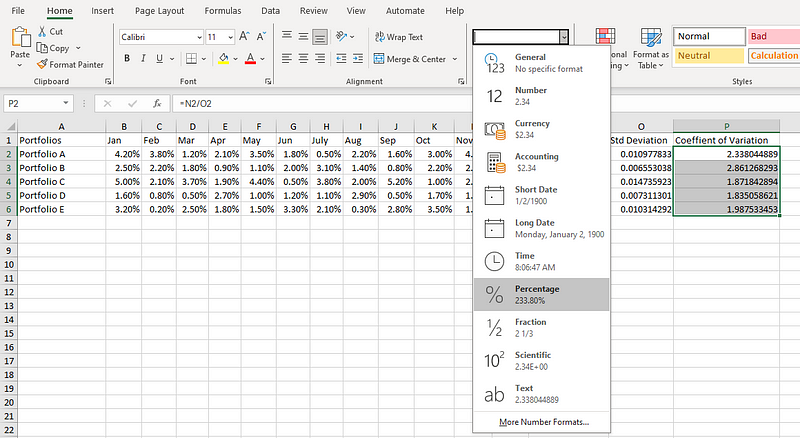
Transformar los valores en porcentajes.

Y ya está, ¡todos nuestros valores CV están en la columna P!

Datos finales con todos los cálculos.

Interpretar el Coeficiente de Variación

Un CV más bajo indica que la cartera tiene un riesgo menor por unidad de rendimiento, lo que sugiere un rendimiento más estable o constante en relación con su rendimiento medio. Un CV más alto sugiere un mayor riesgo por unidad de rendimiento, lo que implica que los rendimientos son volátiles o incoherentes en relación con los rendimientos medios indicados.

Basándonos en los resultados anteriores, podríamos incluir las siguientes conclusiones en nuestro informe:

• La Cartera D ofrece la rentabilidad más baja y también tiene el CV más bajo, lo que la hace potencialmente adecuada para los inversores con aversión al riesgo que priorizan la estabilidad sobre una rentabilidad alta.
• La Cartera B, a pesar de tener una rentabilidad media moderada, tiene la variabilidad más alta (CV más alto), lo que podría ser adecuado sólo para inversores tolerantes al riesgo que puedan soportar fluctuaciones significativas de la rentabilidad.
• La Cartera C podría ser la opción más equilibrada para muchos inversores, gracias a su combinación de mayor rentabilidad y volatilidad relativamente baja. Ofrece un buen equilibrio entre riesgo y recompensa.

Coeficiente de variación: Consideraciones prácticas

Ahora que sabemos qué es el CV y cómo calcularlo en Excel, veamos algunos aspectos prácticos.

El coeficiente de variación con media cero o casi cero

Al interpretar el CV, hay que tener cuidado con las medias cero o casi cero. Esto puede ocurrir si todos nuestros puntos de datos son cero, o si los valores positivos y negativos se equilibran perfectamente. En estos casos, el cálculo del CV intenta dividir por cero, lo que conduce a resultados sin sentido.

Del mismo modo, una media muy pequeña puede inducirnos a error. El CV puede ser extremadamente alto, lo que sugiere una gran variabilidad, aunque la dispersión real de nuestros datos sea mínima. Imagina que analizas los rendimientos de las inversiones con algunos valores ligeramente positivos y otros ligeramente negativos, lo que conduce a una media cercana a cero. El CV podría exagerar el riesgo percibido.

Para medias cero o casi cero, tenemos que considerar medidas alternativas como el rango, el rango intercuartílico o simplemente la desviación típica. Si quieres saber más sobre las medidas de variabilidad, consulta este curso de Introducción a la Estadística.

El coeficiente de variación y la distribución de los datos

El CV funciona mejor cuando los datos tienen una distribución normal, o al menos simétrica. Si nuestros datos están sesgados o tienen valores atípicos, la media y la desviación típica pueden estar sesgadas, lo que conduce a un CV inexacto.

Es útil explorar nuestros datos mediante estadísticas descriptivas o visualizaciones antes de utilizar el CV. Esto nos ayudará a comprender la distribución y a identificar cualquier asimetría o valor atípico que pueda afectar a la fiabilidad del CV.

Si quieres utilizar Excel para visualizar datos, consulta este curso sobre Visualización de datos en Excel.

El coeficiente de variación con escalas de razón e intervalo

El CV es más útil para datos de escala de razón con un punto cero que represente realmente una ausencia la cantidad (por ejemplo, alturas, pesos o precios). En estos casos, un valor cero significa realmente cero: un peso cero significa que no hay peso presente.

Sin embargo, aplicar la CV a datos de intervalo, como temperaturas o fechas, puede ser engañoso. Su punto cero no significa necesariamente una ausencia de la cantidad. Por ejemplo, cero grados Celsius no significa que no haya calor.

Sin embargo, si realizamos transformaciones en los datos de temperatura, como la medición de anomalías de temperatura, donde cero significa inexistencia, entonces se convierte en un caso de uso adecuado.

La conclusión es que, antes de utilizar el CV, debemos considerar si nuestro tipo de datos se ajusta a los supuestos del cálculo del CV para garantizar unos resultados fiables.

Conclusión

El coeficiente de variación (CV) es una valiosa herramienta para los científicos de datos, ya que nos ofrece una forma estandarizada de comparar la variabilidad de los conjuntos de datos aunque utilicen unidades diferentes. Como hemos visto, tiene aplicaciones en diversos campos como las finanzas, la fabricación y el análisis meteorológico.

Calcular el CV en Excel es un proceso sencillo. Aprovechando las funciones incorporadas para la desviación típica y la media, podemos calcular fácilmente el CV.

Si quieres potenciar tus habilidades de análisis de datos en Excel, considera este curso sobre Análisis de Datos en Excel.