So berechnest du den Variationskoeffizienten in Excel

Als Datenwissenschaftler ist es wichtig, die Variabilität unserer Daten zu verstehen. Der Variationskoeffizient (VK) ist eine nützliche Kennzahl, die diese Variabilität als Anteil des Mittelwerts ausdrückt und den Vergleich von Datensätzen mit unterschiedlichen Einheiten ermöglicht.

In diesem Lernprogramm lernst du den Variationskoeffizienten als statistisches Konzept kennen und erfährst, wie du den Variationskoeffizienten in Excel ermitteln kannst.

Wenn du auf der Suche nach einer umfassenden Einführung in Excel bist, solltest du dir den fünfteiligen Kurs "Excel Grundlagen" ansehen.

Sehen wir uns zunächst eine sehr kurze Antwort an und fügen dann weitere Details hinzu.

Kurze Antwort: So berechnest du den Variationskoeffizienten in Excel

Hier ist die Schritt-für-Schritt-Anleitung zur Ermittlung des Variationskoeffizienten in Excel:

• Berechne die Standardabweichung: In eine leere Zelle geben wir die Formel =STDEV.P(A1:A10) ein, wobei wir A1:A10 durch den tatsächlichen Bereich unserer Daten ersetzen.
• Berechne den Mittelwert: In einer anderen leeren Zelle geben wir die Formel =AVERAGE(A1:A10) ein und verwenden dabei denselben Datenbereich.
• Berechne den Variationskoeffizienten: In einer letzten Zelle geben wir die Formel =STDEV.P(A1:A10)/AVERAGE(A1:A10) ein. Dabei wird die Standardabweichung durch den Mittelwert geteilt.

Was ist der Variationskoeffizient?

Der Variationskoeffizient (VK) ist ein statistisches Maß, das die relative Variabilität eines Datensatzes im Verhältnis zu seinem Mittelwert quantifiziert.

In der Regel drücken wir sie als Prozentsatz aus und berechnen sie, indem wir die Standardabweichung des Datensatzes durch den Mittelwert teilen und das Ergebnis mit 100 multiplizieren.

Die Formel zur Berechnung des Variationskoeffizienten lautet:

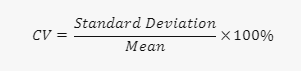
Mit dem CV können wir die Variabilität von zwei oder mehr Datensätzen vergleichen, die unterschiedliche Einheiten oder Mittelwerte haben können.

Ein niedriger CV zeigt an, dass die Datenpunkte näher am Mittelwert liegen, was eine geringere Variabilität widerspiegelt. Umgekehrt deutet ein höherer CV auf eine größere Streuung der Datenpunkte um den Mittelwert hin.

Die Stärke des CV liegt darin, dass er die Variabilität von Datensätzen mit unterschiedlichen Einheiten vergleicht. Das macht sie besonders nützlich in Bereichen wie dem Finanzwesen, wo sie das Risiko-Ertrags-Verhältnis verschiedener Anlageportfolios bewerten kann.

Auch in der Qualitätskontrolle kann der Lebenslauf helfen, die Konsistenz von Produktionsprozessen zu vergleichen, die unterschiedliche Messskalen verwenden.

Werfen wir einen genaueren Blick auf die Anwendungen in der Praxis.

Anwendungen des Variationskoeffizienten

In der Finanzwelt und bei der Risikobewertung nutzen Investoren CV, um Vermögenswerte zu identifizieren, die im Verhältnis zu ihrem Risiko höhere Renditen bieten. So können sie diversifizierte Portfolios aufbauen und Risiken effektiv verwalten. Diese Anwendung ist besonders in Märkten nützlich, in denen die absoluten Renditen aufgrund unterschiedlicher Volatilitätsniveaus irreführend sein könnten.

Der Lebenslauf spielt auch eine wichtige Rolle bei der Qualitätskontrolle in der Produktion. Es hilft, eine gleichbleibende Produktqualität über verschiedene Produktionschargen hinweg zu gewährleisten. Ein niedriger Lebenslauf deutet auf eine geringere Variation der Produkteigenschaften hin, was für die Aufrechterhaltung der Markenstandards und die Kundenzufriedenheit entscheidend ist.

Branchen wie die Pharmaindustrie und die Automobilherstellung, in denen die Zuverlässigkeit der Produkte von größter Bedeutung ist, verlassen sich bei der Bewertung und Kontrolle der Produktionsprozesse stark auf CV.

Forscher und Meteorologen nutzen sie, um die Beständigkeit von Wettermustern zu analysieren, z. B. Niederschlagsschwankungen in verschiedenen Regionen oder Zeiträumen. Diese Analyse hilft dabei, die Genauigkeit der Wettervorhersagen zu verbessern und landwirtschaftliche Aktivitäten zu planen, die stark von den Wetterbedingungen abhängig sind.

Denk daran, dass der CV ein relatives Maß für die Streuung ist. Seine Stärke liegt im Vergleich der Variabilität zwischen mehreren Datensätzen oder Variablen. Sie ist weniger informativ, wenn sie verwendet wird, um die Variabilität eines einzelnen Datensatzes zu beschreiben. Die Anwendungsmöglichkeiten des Lebenslaufs gehen über diese Beispiele hinaus und machen ihn zu einem wertvollen Instrument in vielen Branchen.

Jetzt wollen wir anhand eines Beispiels lernen, wie man den Variationskoeffizienten in Excel berechnet.

So findest du den Variationskoeffizienten in Excel

Im Gegensatz zu anderen Berechnungen in Excel haben wir keine einzeilige Funktion zur Berechnung des Lebenslaufs. Wie wir gleich sehen werden, ist der Prozess aber trotzdem einfach.

Stell dir vor, du bist ein Finanzdatenanalyst, der die Aufgabe hat, für das Vermögensverwaltungsteam eines Unternehmens Investitionsportfolios zu bewerten. Um ihre strategischen Entscheidungen zu treffen, musst du das mit jedem Portfolio verbundene Risiko bewerten. Der Lebenslauf ist hier sehr hilfreich.

Indem du die Standardabweichung der Renditen der einzelnen Portfolios mit dem Renditemittelwert vergleichst, kannst du ihre Risiko-Rendite-Profile bestimmen. Dieses Maß kann zeigen, welche Portfolios im Verhältnis zum Risiko höhere Renditen bieten.

Um den Variationskoeffizienten jedes Portfolios zu berechnen, stellen wir zunächst die Renditen der einzelnen Portfolios für jeden Monat des Jahres zusammen:

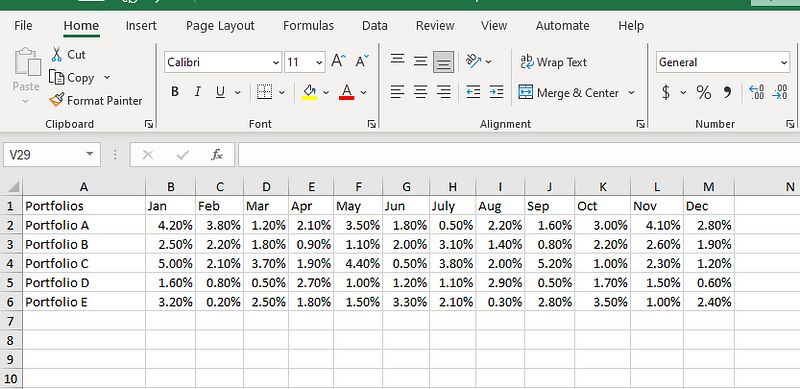
Daten zu den Portfoliorenditen.

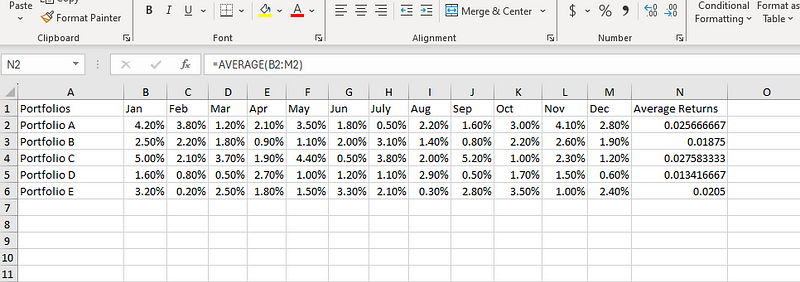
Wir berechnen den Mittelwert für jedes Portfolio (denk daran, dass wir für die Formel des Lebenslaufs den Mittelwert kennen müssen). Geben wir die folgende Formel in die Zelle N2 ein:

=AVERAGE(B2:M2)

Berechne den Mittelwert in Excel.

Jetzt ziehen wir den Füllgriff (das kleine Quadrat in der rechten unteren Ecke von N2), um die Formel auf die anderen Portfolios auszuweiten.

Ausdehnung des berechneten Mittelwerts auf andere Portfolios.

Wir haben den Mittelwert, aber wir brauchen noch ein weiteres Element für unsere Lebenslaufformel: die Standardabweichung. Wähle O2 und benutze die folgende Formel, um die Standardabweichung zu berechnen:

=STDEV.P(B2:M2)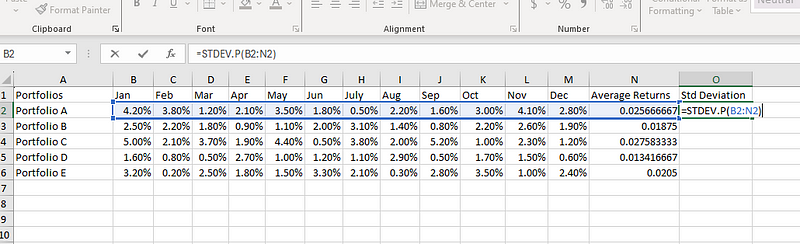

Berechnung der Standardabweichung in Excel.

Jetzt ziehen wir den Füllgriff, um die Formel auf die anderen Portfolios auszuweiten. Nebenbei bemerkt: Wir haben STDEV.P() statt STDEV.S() verwendet, weil wir in unserem Beispiel davon ausgehen, dass unser Datensatz eine Grundgesamtheit und keine Stichprobe ist.

Da wir nun sowohl den Mittelwert als auch die Standardabweichung kennen, können wir den CV berechnen. Teilen wir die Standardabweichung durch den Mittelwert in P2:

=N2/O2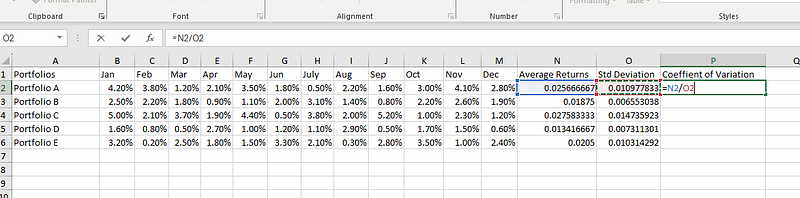

Berechne den Variationskoeffizienten in Excel.

Wie zuvor ziehen wir den Füllgriff, um die Formel auf die übrigen Portfolios auszuweiten.

Da der Lebenslauf in der Regel in Prozent ausgedrückt wird, wählen wir P2 bis P6 und ändern die Zahlenformatierung in Prozent, wie im folgenden Diagramm dargestellt.

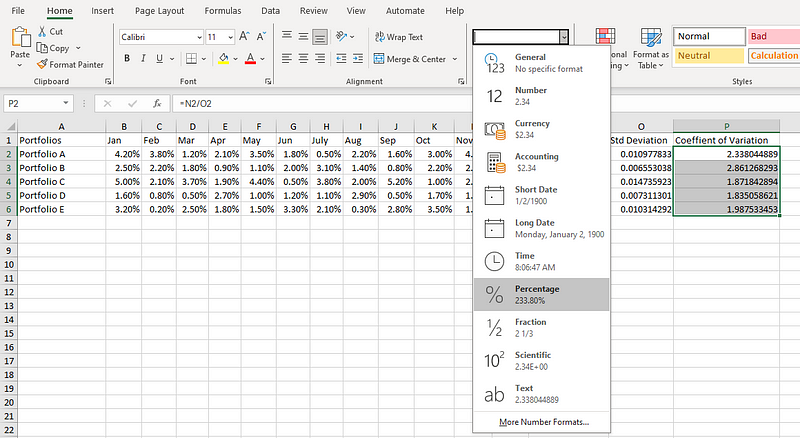
Umrechnung der Werte in Prozentwerte.

Und das war's, alle unsere CV-Werte stehen in der Spalte P!

Endgültige Daten mit allen Berechnungen.