Test du khi-deux dans les feuilles de calcul

Test du chi carré

Le test du chi-carré est un test statistique qui peut être utilisé pour déterminer quelles fréquences observées sont significativement différentes des fréquences attendues ou non dans une ou plusieurs catégories(Source). Dans l'expression mathématique, il s'agit du rapport entre les résultats/fréquences observés expérimentalement (O) et les résultats théoriquement attendus (E) sur la base de certaines hypothèses, ou il est calculé en divisant l'écart global entre les fréquences observées et attendues par les fréquences attendues.

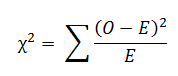
S'il n'y a pas de différence entre les fréquences observées et les fréquences attendues, la valeur du chi-carré sera nulle. S'il y a une différence, la valeur du chi carré sera supérieure à zéro.

En comparant la valeur calculée avec les valeurs du tableau, vous devez calculer le degré de liberté. Vous pourrez ensuite comparer et tirer une conclusion.

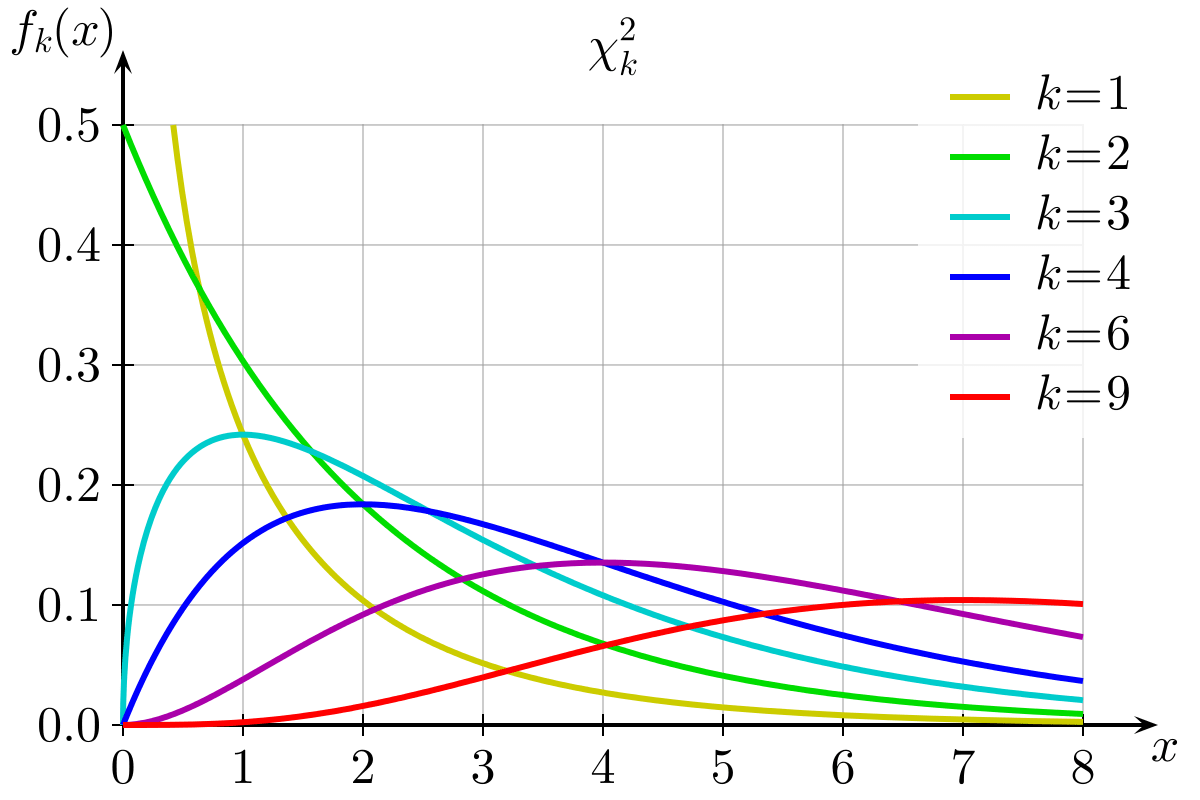
Graphique de la distribution de probabilité du khi-deux : Source de l'image :

Il existe trois types de tests chi-carré :

• Qualité de l'ajustement
• Test d'indépendance
• Test d'homogénéité

Terminologie

• Tableau de contingence : Il s'agit d'un tableau croisé ou d'un tableau à double entrée. Vous utilisez cette méthode pour afficher une variable dans une ligne et une autre dans une colonne avec leur fréquence. Il s'agit d'un type de tableau de distribution de fréquence des variables catégorielles.

• Fréquences observées : Sont des comptages effectués à partir de données expérimentales. En d'autres termes, vous observez les données et prenez des mesures. (Source)

• Fréquences attendues : Les chiffres sont-ils calculés à l'aide de la théorie des probabilités ? Les fréquences attendues sont calculées pour chaque cellule du tableau de contingence.

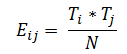
Où ?

• Eij : Fréquence attendue pour la ième ligne et la jième colonne
• Ti : Total de la ième ligne
• Tj : Total de la jème ligne
• N : Total général

Vous pouvez aussi l'exprimer sous la forme suivante : (total des lignes * total des colonnes) / total général.

• Hypothèse nulle (H0) : Elle indique qu'il n'existe aucune association entre les deux variables croisées dans la population. Les variables sont donc statistiquement indépendantes. Par exemple, si vous comparez deux méthodes A et B pour savoir laquelle est la plus efficace ou laquelle fonctionne le mieux, et si l'hypothèse est que les deux méthodes sont aussi bonnes l'une que l'autre, cette hypothèse est appelée l'hypothèse nulle.

• Hypothèse alternative (HA) : Elle propose que les deux variables soient liées à la population. Si vous supposez que, parmi deux méthodes, la méthode A est supérieure à la méthode B ou que la méthode B est supérieure à la méthode A, cette hypothèse est appelée hypothèse alternative.

• Degré de liberté : Le nombre de variables indépendantes qui composent la statistique est appelé le degré de liberté de cette statistique.

Où ?

• r=nombre de lignes
• c=nombre de colonnes

Elle sera utilisée pour le test d'indépendance et le test d'homogénéité, et non pour la qualité de l'ajustement.

• Test du khi-deux Statistiques : La statistique du chi-carré est un chiffre unique qui vous indique l'écart entre les chiffres observés et les chiffres auxquels vous vous attendriez s'il n'y avait aucune relation dans la population.
• Valeur du chi carré : La valeur P du chi-deux vous indiquera si les résultats de votre test sont significatifs ou non.

Types de test du khi-deux

1. Qualité de l'ajustement : Le test d'adéquation du chi carré est un test non paramétrique utilisé pour déterminer dans quelle mesure la valeur observée d'un phénomène donné est significativement différente de la valeur attendue. Dans ce test, vous n'avez qu'une seule variable provenant d'une seule population(Source).

   • Hypothèse nulle (H0) : Dans le test d'adéquation du chi carré, l'hypothèse nulle suppose qu'il n'y a pas de différence significative entre la valeur observée et la valeur attendue(Source).

   • Hypothèse alternative (Ha) : Dans le test d'adéquation du chi carré, l'hypothèse alternative suppose qu'il existe une différence significative entre la valeur observée et la valeur attendue(Source).

     Prenons un exemple simple : vous avez lancé 120 fois un dé à 6 faces et obtenu les fréquences observées.

D'où,

• H0 = Les chances d'obtenir tous les nombres à la même fréquence sont égales, ou les données sont conformes à celles attendues.

          p1 = p2 = p3 = p4 = p5 = p6 = 1/6
  

• Ha = Au moins un p n'est pas égal à 1/6, ou les données ne sont pas cohérentes avec celles attendues.

  • Critères et règles de décision : La région de rejet est toujours unilatérale droite en utilisant la distribution χ2 avec (k-1) degré de liberté. (k = nombre de catégories) Rejeter H0 si χ2calculé > χ2tabulé DOF = k-1

• Test d'indépendance: vous utilisez ce test pour vérifier si deux variables catégorielles sont indépendantes ou non. par exemple, indépendance entre le sexe et l'opinion.

H0 : La variable de la ligne est indépendante de la variable de la colonne, ou il n'y a pas de relation significative entre les variables Ha : La relation est importante.

• Critères et règles de décision : La région de rejet est toujours à queue droite en utilisant la distribution χ2 avec (r-1)(c-1) degré de liberté. (r = nombre de lignes, c = nombre de colonnes)

  Rejeter H0 si χ2calculé > χ2tabulé

  DOF = (r-1)(c-1)

1. Test d'homogénéité : Lorsque vous souhaitez tester si les fréquences de différentes populations sont distribuées de manière identique ou non. Dans ce cas, vous effectuez le test d'homogénéité. Prenons un exemple pour l'appréhender de manière plus pratique. Dans une enquête, vous avez demandé si les revenus étaient faibles, moyens ou élevés. Dans cette enquête, les deux populations sont diversifiées, hommes et femmes. Dans ce cas, vous effectuez un test d'homogénéité du chi carré pour déterminer si les revenus des hommes et des femmes diffèrent de manière significative ou non.

H0 : Le nombre de fréquences est le même dans toute la population. Ha : Le nombre de fréquences est différent d'une population à l'autre.

• Critères et règles de décision : La région de rejet est toujours à queue droite en utilisant la distribution χ2 avec (r-1)(c-1) degré de liberté. (r = nombre de lignes, c = nombre de colonnes)

  Rejeter H0 si χ2calculé > χ2tabulé

  DOF = (r-1)(c-1)

Exemple de test du khi-deux

Supposons que vous souhaitiez classer les défauts des meubles produits par une usine de fabrication en fonction du type de défauts et de l'équipe de production. Au total, 390 défauts de meubles ont été enregistrés et classés dans l'un des quatre types A, B, C et D. En même temps, chaque meuble défectueux a été identifié en fonction de l'équipe de production.

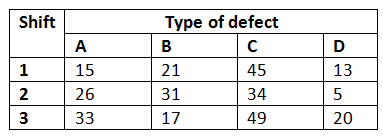
Source : Livre sur les statistiques de l'ingénierie

Solution : vous devez déterminer si les types de défauts dépendent ou non de l'équipe de production. Nous allons donc résoudre ce problème à l'aide d'Excel.

Résolution de l'exemple à l'aide du test du khi-deux dans les feuilles de calcul

Commençons par introduire ces données dans la feuille de calcul

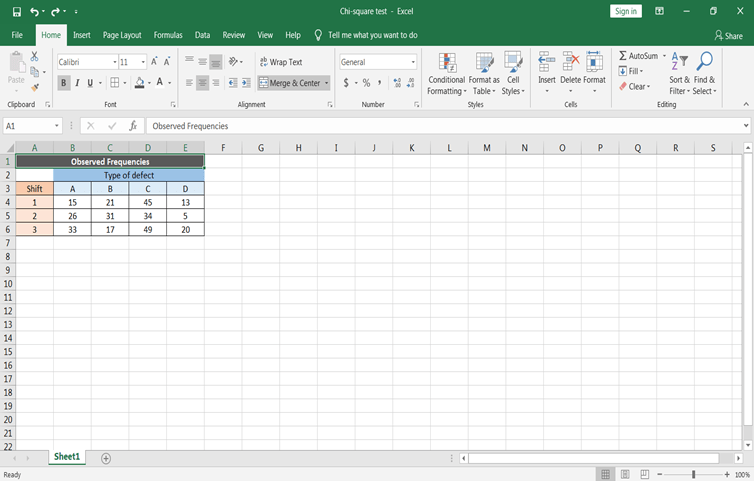
Définir l'hypothèse nulle et l'hypothèse alternative

Définir l'hypothèse nulle et l'hypothèse alternative dans la section précédente. L'objectif principal est de vérifier si les défauts des meubles sont indépendants de l'équipe de production ou non :

• H0 = Le type de défaut et l'équipe de fabrication sont indépendants
• Ha = Le type de défaut et le changement de fabrication sont dépendants

Calcul des fréquences attendues

• Avant de calculer les fréquences attendues. Tout d'abord, calculez la somme des éléments sur chaque ligne et la somme des éléments sur chaque colonne à l'aide de la fonction SUM(), ce qui correspond respectivement au total de la ligne et au total de la colonne. Calculez également le total des lignes et des colonnes. Le total des lignes et des colonnes sera le même.

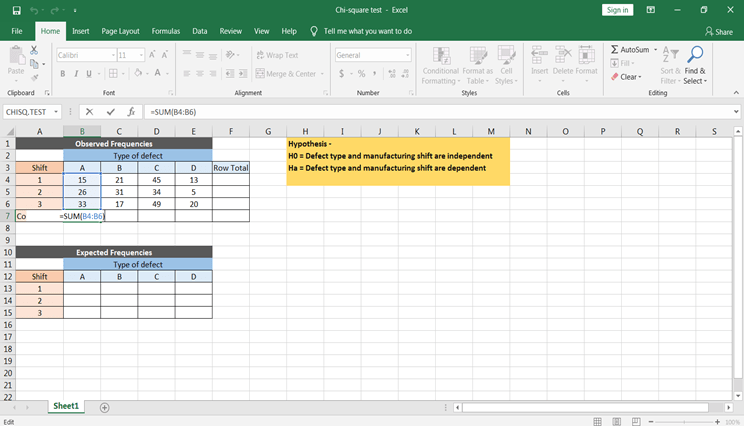
• Comme vous le savez, la fréquence attendue = (total des lignes * total des colonnes) / total

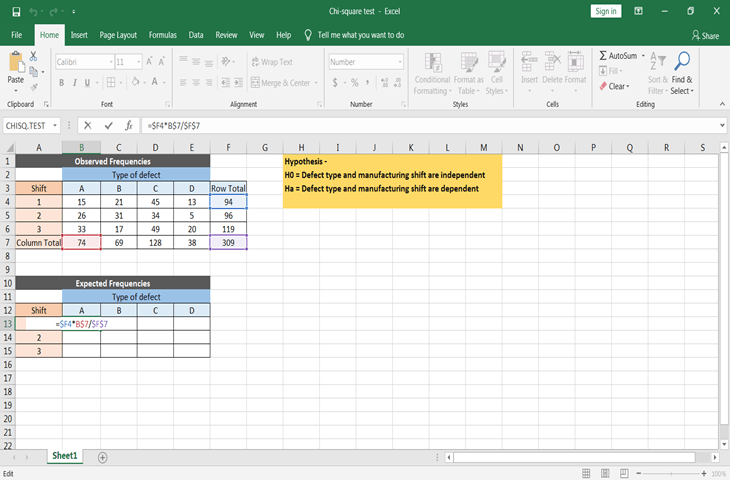
N'oubliez pas de rendre les cellules absolues lors de l'application de la formule, afin de pouvoir copier et coller la formule pour toutes les valeurs attendues.

Calculer la valeur de Chi-statistique

Avant de calculer la valeur de la statistique du chi ou la valeur p, supposons d'abord le niveau de signification. Cela signifie à quel niveau de signification vous voulez connaître la réponse. Supposons un niveau de signification α = 0,05. De même, le degré de liberté serait = (r-1)(c-1) = (3-1)(4-1) = 6.

Il y a deux façons de calculer la valeur du chi statistique : par la formule χ^2= ∑(O-E)^2/E ou en utilisant la fonction excel pour obtenir la valeur du chi statistique.

Calculons d'abord à l'aide de la formule. Pour cela, vous devez calculer ∑(O-E)^2/E à l'aide d'excel. Pour ce faire, suivez les étapes suivantes -

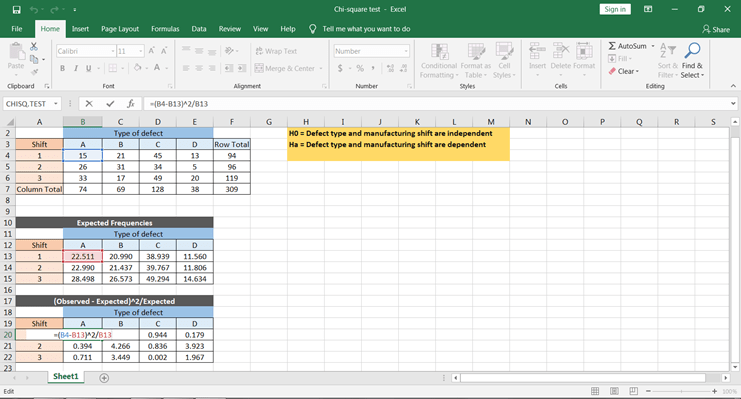
Vous pouvez obtenir toutes les valeurs en copiant et collant cette formule dans toutes les cellules.

Pour obtenir les valeurs χ^2, il faut prendre la somme de toutes les valeurs, ce qui nous donne la valeur calculée de la statistique du chi-carré.

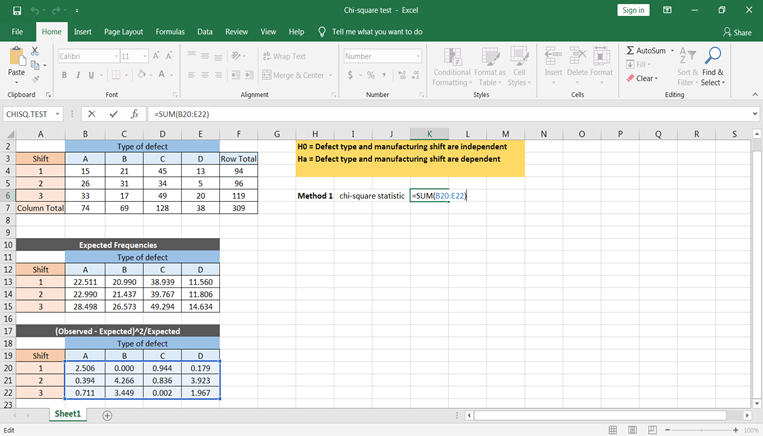
Sur la base des valeurs tabulées et calculées, vous pouvez conclure que les types de défauts et les temps de travail sont interdépendants.

Calculons maintenant à l'aide de la fonction Excel. La fonction CHISQ.TEST() donne la valeur p, qui peut être directement comparée au niveau de signification pour conclure les résultats.

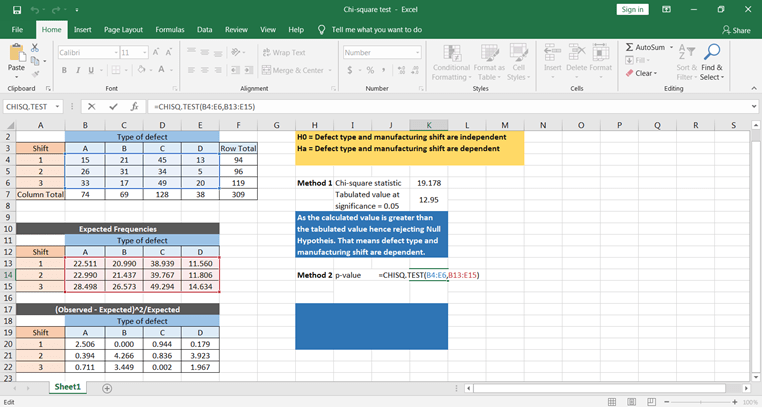
Sur la base de la valeur p, vous pouvez conclure que le défaut dépend de la durée de l'équipe de fabrication.

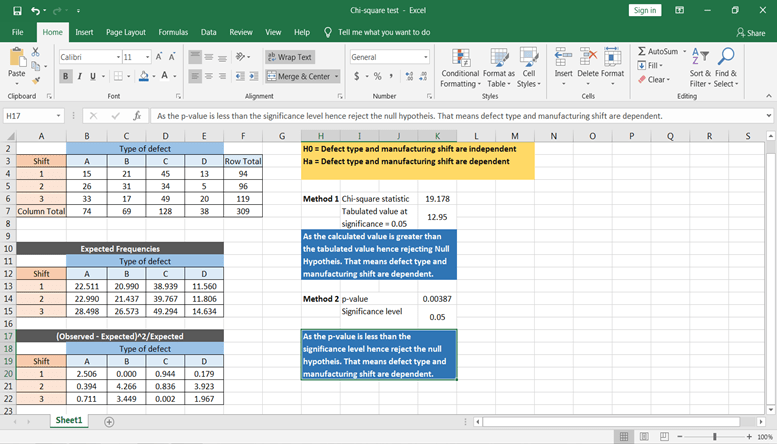
Avantages et inconvénients

Pour :

• Il est plus facile à calculer.
• Il peut également être utilisé avec des données nominales.
• Il ne présume rien de la distribution des données.

Cons :

• Le nombre d'observations doit être supérieur à 20.
• Les données doivent être des données de fréquence.
• Il suppose un échantillonnage aléatoire. Cela signifie que l'échantillon doit être sélectionné au hasard.
• Il est sensible aux petites fréquences, ce qui conduit à des conclusions erronées.
• Elle est également sensible à la taille de l'échantillon.

Conclusion

Félicitations, vous avez atteint la fin de ce tutoriel !

Dans ce tutoriel, vous avez abordé de nombreux détails sur le test du Khi-deux. Vous avez appris ce qu'est le khi-deux, les terminologies utilisées dans le test du khi-deux, les types de tests du khi-deux, des exemples de tests du khi-deux et un exemple sur la façon de résoudre un test du khi-deux dans des feuilles de calcul. Vous avez également examiné ses avantages et ses inconvénients.

Avec un peu de chance, vous pouvez maintenant utiliser les concepts du chi carré pour tester l'hypothèse. Merci d'avoir lu ce tutoriel !

Consultez notre tutoriel Premiers pas avec les feuilles de calcul.

Si vous souhaitez en savoir plus sur les statistiques dans les feuilles de calcul, suivez le cours Statistics in Spreadsheets de DataCamp.