Chi-Quadrat-Test in Tabellenkalkulationen

Chi-Quadrat-Test

Der Chi-Quadrat-Test ist ein statistischer Test, mit dem festgestellt werden kann, ob die beobachteten Häufigkeiten in einer oder mehreren Kategorien signifikant von den erwarteten Häufigkeiten abweichen oder nicht(Quelle). Im mathematischen Ausdruck ist es das Verhältnis von experimentell beobachteten Ergebnissen/Häufigkeiten (O) und den theoretisch erwarteten Ergebnissen (E) auf der Grundlage bestimmter Hypothesen, oder es wird berechnet, indem die Gesamtabweichung von den beobachteten und erwarteten Häufigkeiten durch die erwarteten Häufigkeiten geteilt wird.

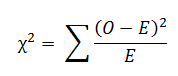
Wenn es keinen Unterschied zwischen den beobachteten und den erwarteten Häufigkeiten gibt, wäre der Chi-Quadrat-Wert gleich null. Wenn es einen Unterschied gibt, dann wäre der Wert des Chi-Quadrats größer als Null.

Wenn du den berechneten Wert mit den Tabellenwerten vergleichst, musst du den Freiheitsgrad berechnen. Dann kannst du vergleichen und eine Schlussfolgerung ziehen.

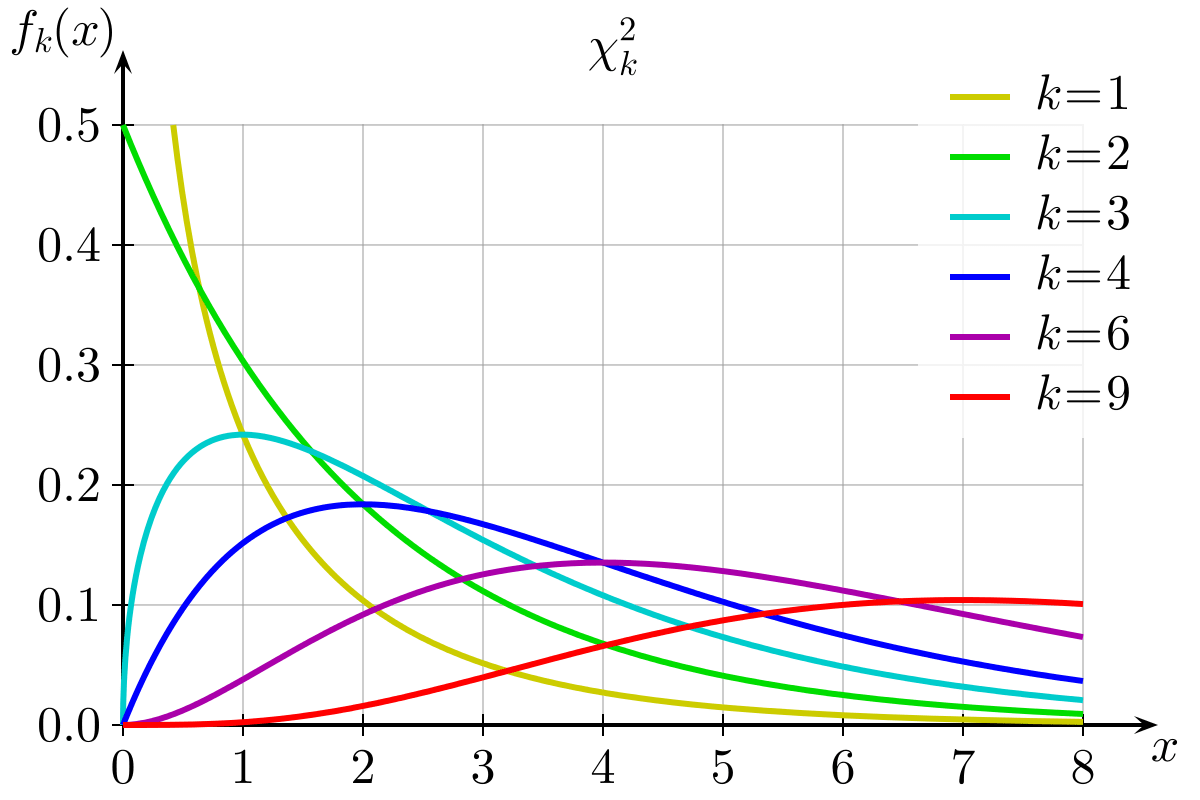
Diagramm der Chi-Quadrat-Wahrscheinlichkeitsverteilung: Bildquelle:

Es gibt drei Arten von Chi-Quadrat-Tests:

• Güte der Passform
• Test der Unabhängigkeit
• Test der Homogenität

Terminologie

• Kontingenztabelle: Dies ist eine Kreuztabelle oder eine Zwei-Wege-Tabelle. Du zeigst die eine Variable in einer Zeile und die andere in einer Spalte mit ihrer Häufigkeit an. Sie ist eine Art Häufigkeitsverteilungstabelle der kategorialen Variablen.

• Beobachtete Frequenzen: Sind Zählungen aus experimentellen Daten. Mit anderen Worten: Du beobachtest das Geschehen und nimmst Messungen vor. (Quelle)

• Erwartete Frequenzen: Sind Zählungen, die mithilfe der Wahrscheinlichkeitstheorie berechnet werden. Die erwarteten Häufigkeiten werden für jede Zelle in der Kontingenztabelle berechnet.

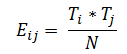
Wo,

• Eij: Erwartete Häufigkeit für die i-te Zeile und j-te Spalte
• Ti: Summe in der i-ten Zeile
• Tj: Summe in der j-ten Zeile
• N: Gesamtbetrag

Du kannst dir das auch so vorstellen: (Zeilensumme * Spaltensumme) / Gesamtsumme

• Nullhypothese (H0): Sie besagt, dass zwischen den beiden kreuztabellierten Variablen in der Population kein Zusammenhang besteht. Daher sind die Variablen statistisch unabhängig. Wenn du zum Beispiel zwei Methoden A und B daraufhin vergleichst, ob sie gleich gut sind oder welche Methode besser funktioniert, und die Annahme ist, dass beide Methoden gleich gut sind, dann wird diese Annahme als Nullhypothese bezeichnet.

• Alternativhypothese (HA): Sie geht davon aus, dass die beiden Variablen mit der Bevölkerung in Verbindung stehen. Wenn du davon ausgehst, dass von zwei Methoden die Methode A der Methode B oder die Methode B der Methode A überlegen ist, dann wird diese Annahme als Alternativhypothese bezeichnet.

• Freiheitsgrad: Die Anzahl der unabhängigen Variablen, aus denen die Statistik besteht, wird als Freiheitsgrad der Statistik bezeichnet.

Wo,

• r=Anzahl der Zeilen
• c=Anzahl der Spalten

Dies wird für den Unabhängigkeitstest und den Homogenitätstest verwendet, nicht für die Anpassungsgüte.

• Chi-Quadrat-Test Statistik: Eine Chi-Quadrat-Statistik ist eine einzelne Zahl, die dir sagt, wie groß der Unterschied zwischen deinen beobachteten Zahlen und den Zahlen ist, die du erwarten würdest, wenn es in der Population überhaupt keine Beziehung gäbe.
• Chi-Quadrat p-value: Der Chi-Quadrat P-Wert sagt dir, ob deine Testergebnisse signifikant sind oder nicht.

Arten von Chi-Quadrat-Tests

1. Die Passgenauigkeit: Der Chi-Quadrat-Anpassungstest ist ein nichtparametrischer Test, der verwendet wird, um herauszufinden, inwieweit sich der beobachtete Wert eines bestimmten Phänomens signifikant vom erwarteten Wert unterscheidet. Bei diesem Test hast du nur eine Variable aus einer einzigen Population(Quelle).

   • Nullhypothese (H0): Bei der Chi-Quadrat-Anpassungsprüfung geht die Nullhypothese davon aus, dass es keinen signifikanten Unterschied zwischen dem beobachteten und dem erwarteten Wert gibt(Quelle).

   • Alternativhypothese (Ha): Beim Chi-Quadrat-Anpassungstest geht die Alternativhypothese davon aus, dass es einen signifikanten Unterschied zwischen dem beobachteten und dem erwarteten Wert gibt(Quelle).

     Nehmen wir ein einfaches Beispiel: Du hast 120 Mal einen fairen sechsseitigen Würfel geworfen und die beobachteten Häufigkeiten erhalten.

Folglich,

• H0 = Die Chancen sind gleich groß, dass alle Zahlen gleich häufig vorkommen, oder die Daten stimmen mit der erwarteten Zahl überein.

          p1 = p2 = p3 = p4 = p5 = p6 = 1/6
  

• Ha = Mindestens ein p ist ungleich 1/6, oder die Daten stimmen nicht mit dem erwarteten überein.

  • Kriterien und Entscheidungsregel: Der Ablehnungsbereich ist immer rechtsschwanzförmig, wobei die χ2-Verteilung mit (k-1) Freiheitsgraden verwendet wird. (k =Anzahl der Kategorien) Verwirf H0, wenn χ2berechnet > χ2tabelliert DOF = k-1

• Unabhängigkeitstest: Mit diesem Test wird geprüft, ob zwei kategoriale Variablen unabhängig sind oder nicht.

H0: Die Zeilenvariable ist unabhängig von der Spaltenvariable, oder es besteht keine signifikante Beziehung zwischen den Variablen Ha: Die Beziehung ist signifikant.

• Kriterien und Entscheidungsregel: Der Ablehnungsbereich ist immer rechtsschwanzförmig, wobei die χ2-Verteilung mit (r-1)(c-1) Freiheitsgraden verwendet wird. (r = Anzahl der Zeilen, c = Anzahl der Spalten)

  Verwirf H0, wenn χ2berechnet > χ2tabuliert

  DOF = (r-1)(c-1)

1. Test der Homogenität: Wenn du testen willst, ob die Häufigkeiten verschiedener Populationen identisch verteilt sind oder nicht. In solchen Fällen führst du den Homogenitätstest durch. Betrachten wir ein Beispiel, um es praktischer zu begreifen. In einer Umfrage hast du nach dem Einkommen gefragt und es als niedrig, mittel oder hoch eingestuft. In dieser Umfrage sind beide Populationen, Männer und Frauen, unterschiedlich. In solchen Fällen führst du einen Chi-Quadrat-Test auf Homogenität durch, um festzustellen, ob sich die Einkommen von Männern und Frauen signifikant unterscheiden oder nicht.

H0: Die Häufigkeitszahl ist in der gesamten Bevölkerung gleich. Ha: Die Häufigkeitsauszählung in der Bevölkerung ist unterschiedlich.

• Kriterien und Entscheidungsregel: Der Ablehnungsbereich ist immer rechtsschwanzförmig, wobei die χ2-Verteilung mit (r-1)(c-1) Freiheitsgraden verwendet wird. (r = Anzahl der Zeilen, c = Anzahl der Spalten)

  Verwirf H0, wenn χ2berechnet > χ2tabuliert

  DOF = (r-1)(c-1)

Beispiel für den Chi-Quadrat-Test

Angenommen, du möchtest die Fehler in den von einer Produktionsstätte hergestellten Möbeln anhand der Art der Fehler und der Produktionsschicht klassifizieren. Insgesamt wurden 390 Möbeldefekte erfasst und die Defekte wurden in die vier Typen A, B, C und D eingeteilt.

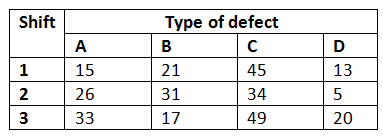
Quelle: Ingenieurstatistik Buch

Lösung: Du musst dir ansehen, ob die Fehlerarten von der Produktionsschicht abhängig sind oder nicht. Lösen wir das Problem also mit Excel.

Lösen des Beispiels mithilfe des Chi-Quadrat-Tests in Tabellenkalkulationen

Fügen wir diese Daten zunächst in das Tabellenblatt ein

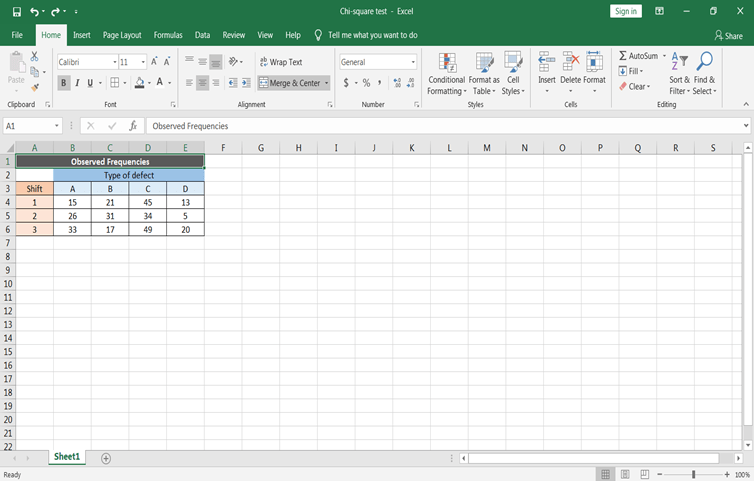
Definieren der Nullhypothese und der Alternativhypothese

Die Null- und die Alternativhypothese im obigen Abschnitt zu definieren. Das Hauptziel ist es, zu prüfen, ob die Möbeldefekte unabhängig von der Produktionsschicht sind oder nicht:

• H0 = Fehlertyp und Fertigungsschicht sind unabhängig
• Ha = Fehlertyp und Fertigungsschicht sind abhängig

Berechnete erwartete Häufigkeiten

• Bevor du die erwarteten Häufigkeiten berechnest. Berechne zunächst die zeilenweise Summe der Elemente für jede Zeile und die spaltenweise Summe der Elemente für jede Spalte mit der Funktion SUMME(), die als Zeilensumme bzw. Spaltensumme bezeichnet wird. Berechne auch die Summe der Zeilensumme und der Spaltensumme. Die Summe der Zeilen und Spalten ist gleich.

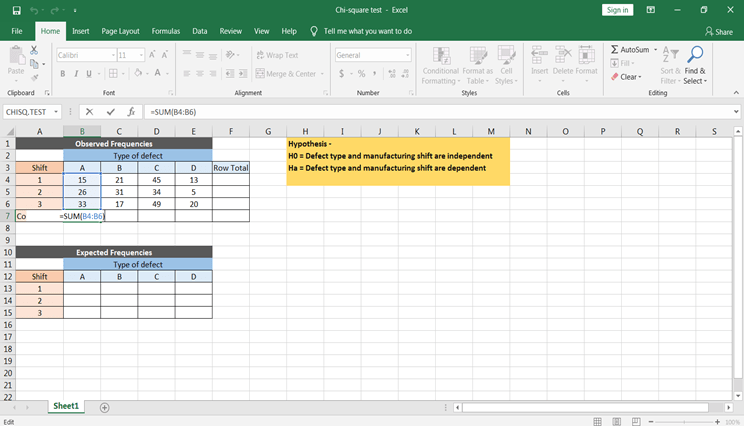
• Wie du weißt, ist die erwartete Häufigkeit = (Zeilensumme * Spaltensumme) / Summe

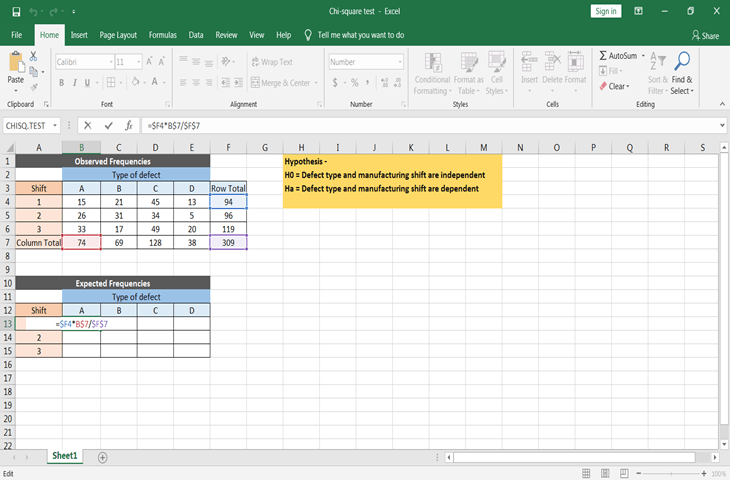
Vergiss nicht, die Zellen beim Anwenden der Formel absolut zu setzen, damit du die Formel für alle erwarteten Werte kopieren und einfügen kannst.

Berechne den Chi-statistischen Wert

Bevor du den Chi-statistischen Wert oder den p-Wert berechnest, musst du zunächst das Signifikanzniveau bestimmen. Das bedeutet, auf welchem Signifikanzniveau du die Antwort wissen willst. Gehen wir von einem Signifikanzniveau α = 0,05 aus. Außerdem wäre der Freiheitsgrad = (r-1)(c-1) = (3-1)(4-1) = 6.

Es gibt zwei Möglichkeiten, die Chi-Quadrat-Statistik zu berechnen: Entweder mit der Formel χ^2= ∑(O-E)^2/E oder mit der Excel-Funktion, um den Wert der Chi-Quadrat-Statistik zu ermitteln.

Rechnen wir zunächst mit der Formel. Dazu musst du ∑(O-E)^2/E mit Excel berechnen. Dies kannst du mit dem folgenden Schritt tun -

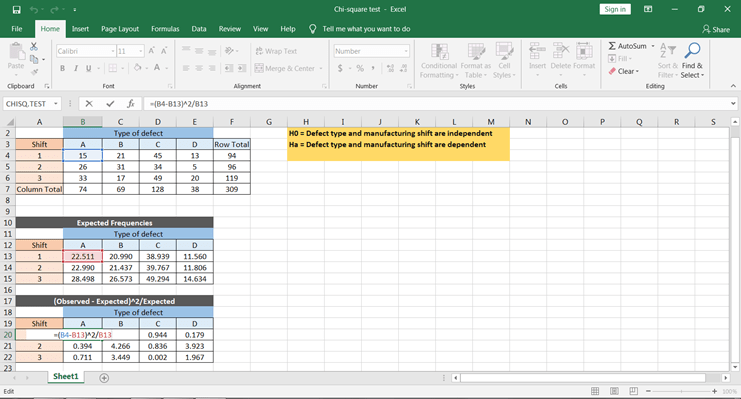
Du kannst alle Werte erhalten, indem du diese Formel kopierst und in alle Zellen einfügst.

Um die χ^2-Werte zu erhalten, nimmst du die Summe aller Werte und erhältst den Wert der Chi-Quadrat-Statistik.

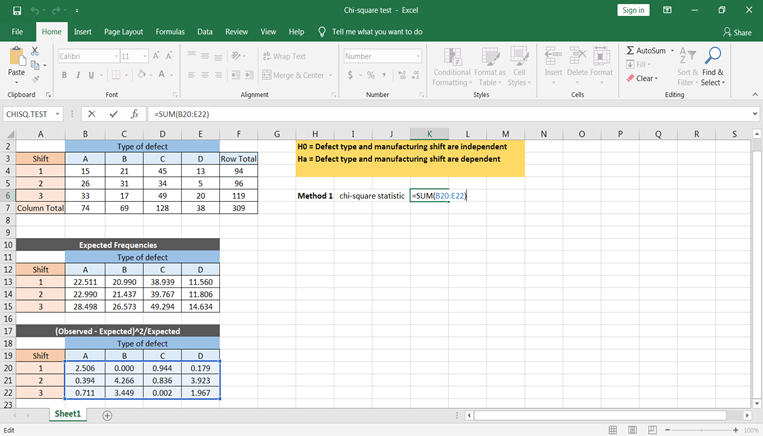
Aus den tabellarischen und berechneten Werten kannst du schließen, dass die Fehlerarten und die Schichtzeiten voneinander abhängig sind.

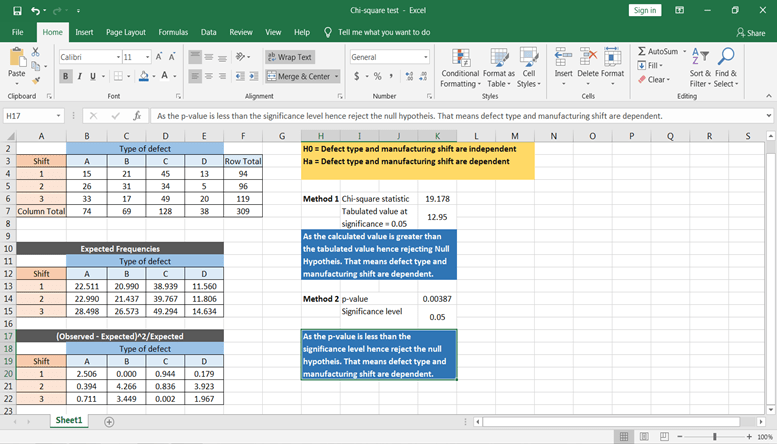
Jetzt wollen wir mit der Excel-Funktion rechnen. Die Funktion CHISQ.TEST() liefert den p-Wert, der direkt mit dem Signifikanzniveau verglichen werden kann, um die Ergebnisse zu ermitteln.

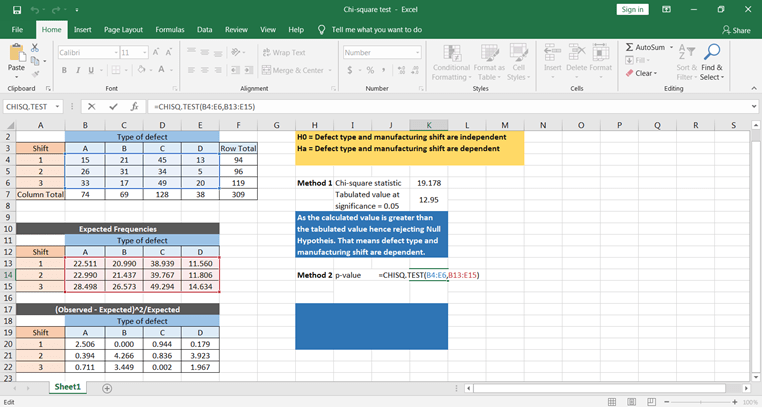
Aus dem p-Wert kannst du schließen, dass der Fehler von der Produktionsschichtzeit abhängt.

Pro und Kontra

Vorteile:

• Es ist einfacher zu berechnen.
• Sie kann auch mit nominalen Daten verwendet werden.
• Sie geht nicht von der Verteilung der Daten aus.

Nachteile:

• Die Anzahl der Beobachtungen sollte mehr als 20 betragen.
• Die Daten müssen Frequenzdaten sein.
• Sie geht von einer Zufallsstichprobe aus. Das bedeutet, dass die Stichprobe nach dem Zufallsprinzip ausgewählt werden sollte.
• Sie ist empfindlich für kleine Frequenzen, was zu falschen Schlussfolgerungen führt.
• Sie ist auch abhängig von der Stichprobengröße.

Fazit

Glückwunsch, du hast es bis zum Ende dieses Tutorials geschafft!

In diesem Lernprogramm hast du viele Details des Chi-Quadrat-Tests behandelt. Du hast gelernt, was ein Chi-Quadrat-Test ist, welche Begriffe beim Chi-Quadrat-Test verwendet werden, welche Arten von Chi-Quadrat-Tests es gibt, welche Beispiele es für Chi-Quadrat-Tests gibt und wie man einen Chi-Quadrat-Test in Tabellenkalkulationen löst. Außerdem hast du dir die Vor- und Nachteile angesehen.

Hoffentlich kannst du jetzt die Chi-Quadrat-Konzepte anwenden, um die Hypothese zu testen. Danke fürs Lesen dieses Tutorials!

Schau dir unser Tutorial "Erste Schritte mit Tabellenkalkulationen" an.

Wenn du mehr über Statistik in Tabellenkalkulationen lernen möchtest, besuche den DataCamp-Kurs Statistik in Tabellenkalkulationen.