Teste de qui-quadrado em planilhas

Teste de qui-quadrado

O teste do qui-quadrado é um teste estatístico que pode ser usado para determinar quais frequências observadas são significativamente diferentes das frequências esperadas ou não em uma ou mais categorias(Fonte). Na expressão matemática, é a razão entre os resultados/frequências observados experimentalmente (O) e os resultados teoricamente esperados (E) com base em determinadas hipóteses, ou é calculada dividindo-se o desvio geral das frequências observadas e esperadas pelas frequências esperadas.

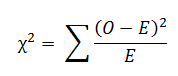
Se não houver diferença entre as frequências observadas e as esperadas, o valor do qui-quadrado será zero. Se houver uma diferença, o valor do qui-quadrado será maior que zero.

Ao comparar o valor calculado com os valores da tabela, você deve calcular o grau de liberdade. Em seguida, você poderá comparar e tirar uma conclusão.

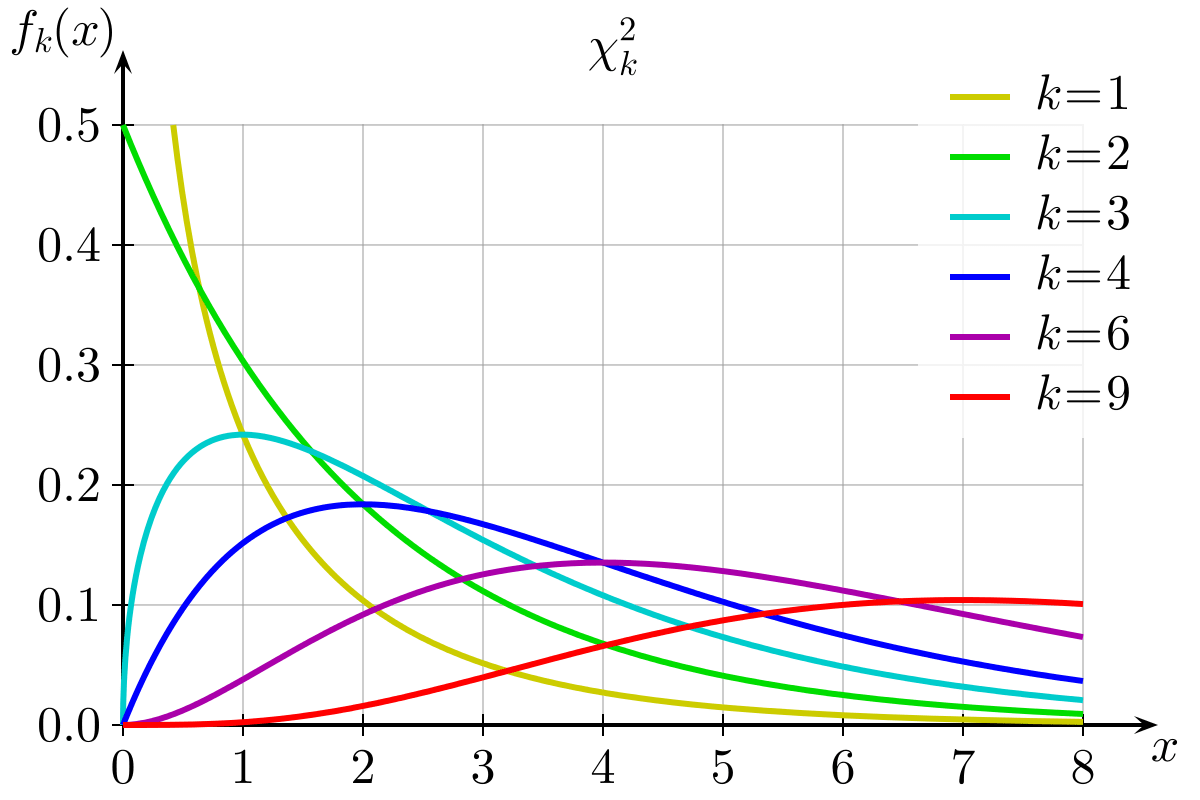
Gráfico de distribuição de probabilidade do qui-quadrado: Fonte da imagem:

Há três tipos de testes de qui-quadrado:

• Adequação
• Teste de independência
• Teste de homogeneidade

Terminologia

• Tabela de contingência: Essa é uma tabela cruzada ou tabela bidirecional. Você usa para mostrar uma variável em uma linha e outra em uma coluna com sua contagem de frequência. É um tipo de tabela de distribuição de frequência das variáveis categóricas.

• Frequências observadas: São contagens feitas a partir de dados experimentais. Em outras palavras, você observa os dados acontecendo e faz medições. (Fonte)

• Frequências esperadas: São contagens calculadas usando a teoria da probabilidade. As frequências esperadas são calculadas para cada célula da tabela de contingência.

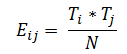
Onde,

• Eij: Frequência esperada para a i-ésima linha e a j-ésima coluna
• Ti: Total na i-ésima linha
• Tj: Total na j-ésima linha
• N: Total geral

Ou você pode pensar nisso como (total da linha * total da coluna) / total geral

• Hipótese nula (H0): Afirma que não existe associação entre as duas variáveis de tabulação cruzada na população. Portanto, as variáveis são estatisticamente independentes. Por exemplo, se você comparar dois métodos A e B quanto à sua qualidade ou qual deles funciona melhor, e se a suposição for de que ambos os métodos são igualmente bons, essa suposição é conhecida como Hipótese Nula.

• Hipótese alternativa (HA): Ele propõe que as duas variáveis estão relacionadas à população. Se você presumir que, de dois métodos, o método A é superior ao método B ou o método B é superior ao método A, essa suposição é conhecida como Hipótese Alternativa.

• Grau de liberdade: O número de variantes independentes que compõem a estatística é conhecido como o grau de liberdade dessa estatística.

Onde,

• r=número de linhas
• c=número de colunas

Isso será usado no teste de independência e no teste de homogeneidade, não na adequação do ajuste.

• Estatísticas do teste de qui-quadrado: Uma estatística qui-quadrado é um número único que informa quanta diferença existe entre as contagens observadas e as contagens que você esperaria se não houvesse nenhuma relação na população.
• Valor de p do qui-quadrado: O valor P do qui-quadrado lhe dirá se os resultados do teste são significativos ou não.

Tipos de teste qui-quadrado

1. Adequação: O teste de adequação do qui-quadrado é um teste não paramétrico usado para descobrir como o valor observado de um determinado fenômeno é significativamente diferente do valor esperado. Neste teste, você tem apenas uma variável de uma única população(Fonte).

   • Hipótese nula (H0): No teste de adequação do qui-quadrado, a hipótese nula pressupõe que não há diferença significativa entre o valor observado e o valor esperado(Fonte).

   • Hipótese alternativa (Ha): No teste de adequação do qui-quadrado, a hipótese alternativa pressupõe que há uma diferença significativa entre o valor observado e o valor esperado(Fonte).

     Por exemplo, vamos dar um exemplo simples: você lançou um dado justo de 6 lados 120 vezes e obteve as frequências observadas.

Portanto,

• H0 = As chances são iguais de obter todos os números na mesma frequência, ou os dados são consistentes com o esperado.

          p1 = p2 = p3 = p4 = p5 = p6 = 1/6
  

• Ha = Pelo menos um p não é igual a 1/6, ou os dados não são consistentes com o esperado.

  • Critérios e regras de decisão: A região de rejeição é sempre de cauda direita usando a distribuição χ2 com (k-1) grau de liberdade. (k = número de categorias) Rejeitar H0 se χ2calculado > χ2tabulado DOF = k-1

• Teste de independência: é usado para testar se duas variáveis categóricas são independentes ou não. Por exemplo, independência de gênero vs. opinião.

H0: A variável da linha é independente da variável da coluna, ou não há relação significativa entre as variáveis Ha: O relacionamento é significativo.

• Critérios e regras de decisão: A região de rejeição é sempre de cauda direita usando a distribuição χ2 com grau de liberdade (r-1)(c-1). (r = número de linhas, c = número de colunas)

  Rejeitar H0 se χ2calculado > χ2tabulado

  DOF = (r-1)(c-1)

1. Teste de homogeneidade: Sempre que você quiser testar se essas frequências de diferentes populações são distribuídas de forma idêntica ou não. Nesses casos, você realiza o teste de homogeneidade. Vamos considerar um exemplo para entender isso de forma mais prática. Em uma pesquisa, você perguntou sobre a renda como baixa, média ou alta. Nesta pesquisa, ambas as populações são diversas, como homens e mulheres. Nesses casos, você realiza um teste qui-quadrado de homogeneidade para determinar se a renda de homens e mulheres difere significativamente ou não.

H0: A contagem de frequência em toda a população é a mesma. Ha: A contagem de frequência na população é diferente.

• Critérios e regras de decisão: A região de rejeição é sempre de cauda direita usando a distribuição χ2 com grau de liberdade (r-1)(c-1). (r = número de linhas, c = número de colunas)

  Rejeitar H0 se χ2calculado > χ2tabulado

  DOF = (r-1)(c-1)

Exemplo de teste de qui-quadrado

Suponha que você queira classificar os defeitos nos móveis produzidos por uma fábrica com base no tipo de defeitos e no turno de produção. Foram registrados 390 defeitos em móveis, e os defeitos foram classificados em quatro tipos: A, B, C e D. Ao mesmo tempo, cada peça de mobiliário com defeito foi identificada de acordo com o turno de produção.

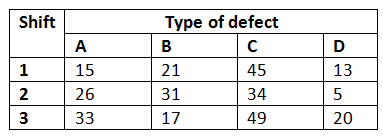
Fonte: Livro de Estatística de Engenharia

Solução: você precisa verificar se os tipos de defeitos dependem ou não do turno de produção. Então, vamos resolver isso usando o Excel.

Como resolver o exemplo usando o teste de qui-quadrado em planilhas

Vamos primeiro colocar esses dados na planilha

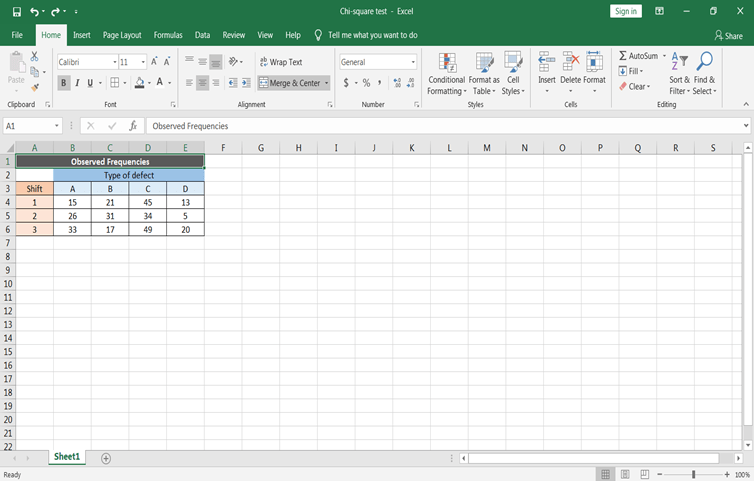
Definição da hipótese nula e da hipótese alternativa

Para definir as hipóteses nula e alternativa na seção acima. O principal objetivo é verificar se os defeitos dos móveis são independentes do turno de produção ou não:

• H0 = O tipo de defeito e o turno de fabricação são independentes
• Ha = O tipo de defeito e o turno de fabricação são dependentes

Frequências esperadas calculadas

• Antes de calcular as frequências esperadas. Primeiro, calcule a soma de itens por linha para cada linha e a soma de itens por coluna para cada coluna usando a função SUM(), que é conhecida como total de linha e total de coluna, respectivamente. Além disso, calcule o total do total da linha e o total da coluna. O total de linhas e colunas será o mesmo.

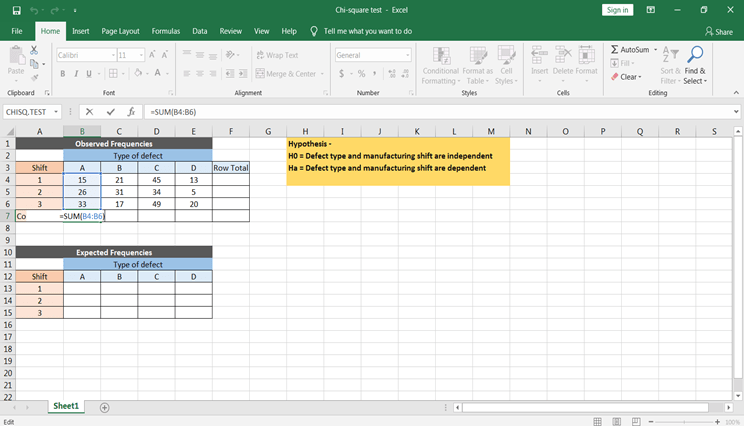
• Como você sabe, frequência esperada = (total da linha * total da coluna) / total

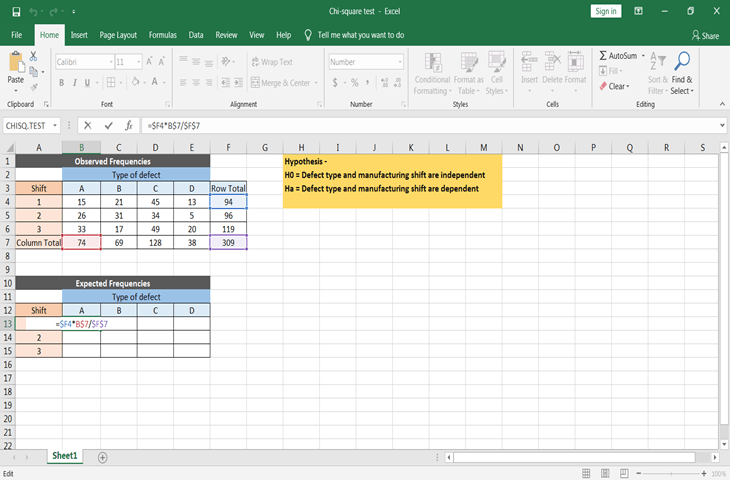
Não se esqueça de tornar as células absolutas ao aplicar a fórmula, para que você possa copiar e colar a fórmula para todos os valores esperados.

Calcular o valor da estatística de Chi

Agora, antes de calcular o valor da estatística Chi ou o valor p, vamos primeiro assumir o nível de significância. Isso significa em que nível de significância você deseja saber a resposta. Vamos supor que o nível de significância α = 0,05. Além disso, o grau de liberdade seria = (r-1)(c-1) = (3-1)(4-1) = 6.

Agora, há duas maneiras de calcular o valor da estatística qui-quadrado: uma pela fórmula χ^2= ∑(O-E)^2/E ou usar a função do Excel para obter o valor da estatística qui-quadrado.

Primeiro, vamos calcular usando a fórmula. Para isso, você precisa calcular ∑(O-E)^2/E usando o Excel. Isso pode ser feito por meio da etapa abaixo

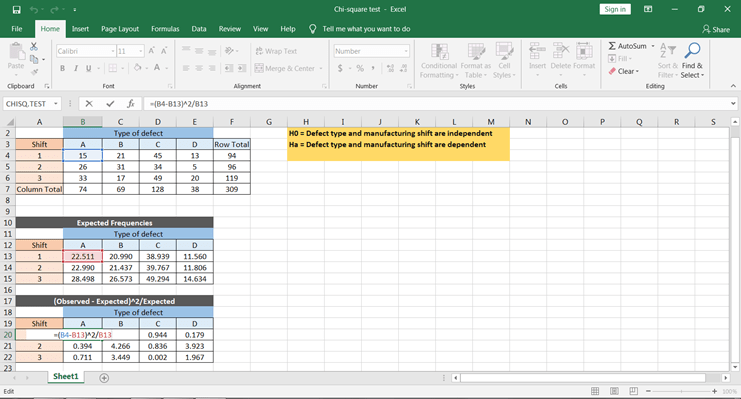
Você pode obter todos os valores copiando e colando essa fórmula em todas as células.

Para obter os valores de χ^2, é necessário obter a soma de todos os valores, o que nos daria o valor calculado da estatística qui-quadrado.

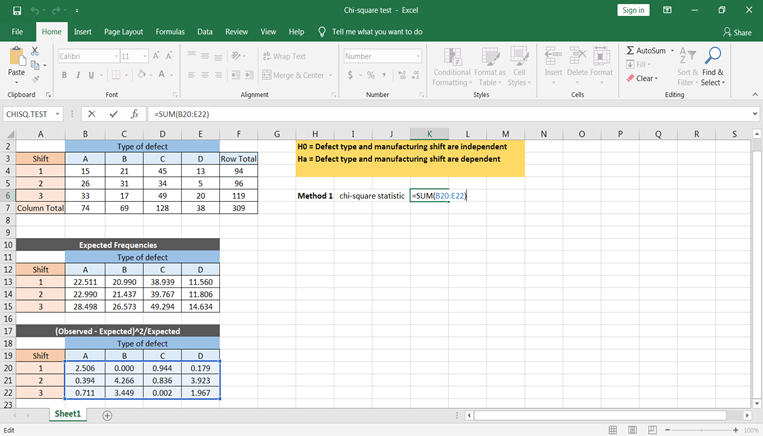
Com base no valor tabulado e calculado, você pode concluir que os tipos de defeitos e os tempos de turno são dependentes.

Agora vamos calcular usando a função do Excel. A função CHISQ.TEST() fornecerá o valor p, que pode ser comparado diretamente com o nível de significância para concluir os resultados.

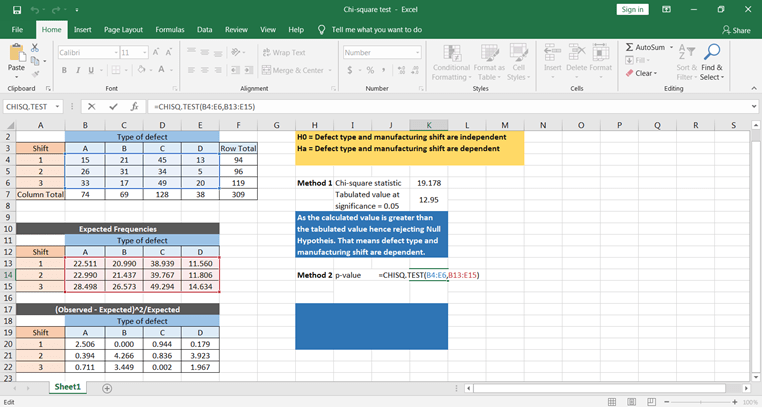
Com base no valor de p, você pode concluir que o defeito depende do tempo do turno de fabricação.

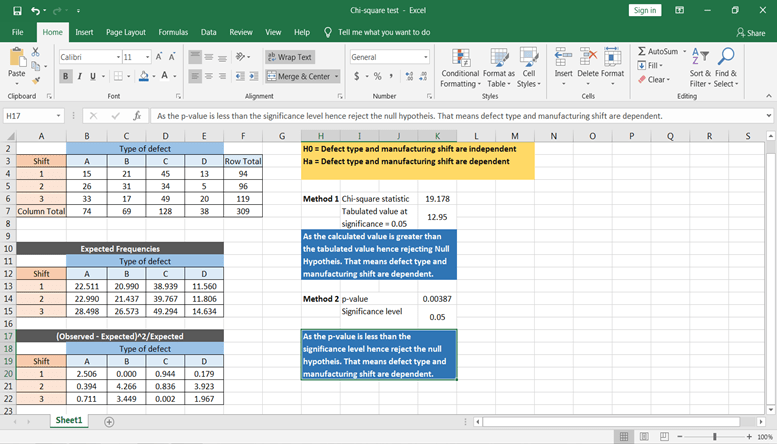
Prós e contras

Prós:

• É mais fácil de calcular.
• Ele também pode ser usado com dados nominais.
• Ele não pressupõe nada sobre a distribuição de dados.

Contras:

• O número de observações deve ser superior a 20.
• Os dados devem ser dados de frequência.
• Ele pressupõe amostragem aleatória. Isso significa que a amostra deve ser selecionada aleatoriamente.
• Ele é sensível a pequenas frequências, o que leva a conclusões errôneas.
• Ele também é sensível ao tamanho da amostra.

Conclusão

Parabéns, você chegou ao final deste tutorial!

Neste tutorial, você abordou muitos detalhes sobre o teste qui-quadrado. Você aprendeu o que é qui-quadrado, as terminologias usadas no teste qui-quadrado, os tipos de testes qui-quadrado, exemplos de testes qui-quadrado e um exemplo de como resolver um teste qui-quadrado em planilhas. Além disso, você analisou seus prós e contras.

Esperamos que agora você possa utilizar os conceitos do qui-quadrado para testar a hipótese. Obrigado por ler este tutorial!

Confira nosso tutorial de Introdução às Planilhas.

Se estiver interessado em aprender mais sobre estatísticas em planilhas, faça o curso Statistics in Spreadsheets do DataCamp.