Test exact de Fisher : Prendre des décisions avec de petits échantillons

Les organisations prennent quotidiennement des décisions en fonction du comportement des clients, des performances des produits et des fluctuations des opérations. Afin de garantir que ces décisions reposent sur des relations et des modèles sous-jacents authentiques dans les données, les analystes ont fréquemment recours à des tests statistiques. 

Bien que les tests statistiques courants fonctionnent bien pour les grands ensembles de données, les entreprises n'ont pas toujours la possibilité de travailler avec de tels ensembles. En réalité, de nombreuses décisions doivent être prises à partir d'échantillons de petite taille, de segments de clientèle spécialisés ou d'événements peu fréquents. Dans ces situations, les tests traditionnels, tels que le test du chi carré, peuvent s'avérer insuffisants, soit en produisant des résultats trompeurs, soit en manquant de la précision nécessaire pour agir en toute confiance sur la base des informations obtenues. 

C'est là que le test exact de Fisher s'avère utile. Veuillez continuer à lire et je vous expliquerai comment procéder.

Qu'est-ce que le test exact de Fisher ?

Le test exact de Fisher est utilisé pour évaluer l'association entre des variables catégorielles lorsque les données sont limitées. Elle est le plus souvent appliquée à des tableaux de contingence 2×2 et calcule la probabilité exacte d'observer des données aussi extrêmes que celles qui ont été collectées, en supposant que l'hypothèse nulle d'indépendance soit vraie.

Un analyste peut utiliser le test exact de Fisher, par exemple, pour évaluer l'efficacité d'une campagne de marketing ciblée. Si, par exemple, l'analyste évaluait l'efficacité d'une campagne par e-mail d' s par rapport à une campagne sur les réseaux sociaux, et ce pour un groupe de clients niche avec des échantillons de petite taille, il pourrait créer un tableau de contingence et effectuer le test exact de Fisher. Dans le cadre d'un contrôle qualité, un analyste pourrait également utiliser le test pour relever les défis liés au signalement des incidents et au suivi des défauts. Lorsque certains types de défaillances ne se produisent que rarement, le test exact de Fisher permet de déterminer si des facteurs tels que le type de machine sont réellement liés à l'apparition de défauts.

Théorie statistique et fondements mathématiques

Après avoir développé une compréhension intuitive de l'importance du test, nous pouvons maintenant le formaliser. À la base, le test exact de Fisher est une méthode statistique utilisée pour déterminer s'il existe une association non aléatoire entre deux variables catégorielles. Elle est le plus souvent appliquée à des tableaux de contingence 2×2 afin de comparer deux groupes à travers deux résultats, par exemple « traitement par rapport à contrôle » contre « amélioration par rapport à absence d'amélioration ».

Il est intéressant de noter que ses origines remontent à l'une des histoires les plus célèbres en statistique, connue sous le nom d'expérience de la « dame dégustant du thé ». Sir Ronald A. Fisher a conçu une expérience pour évaluer le Dr. Muriel Bristol affirmait pouvoir déterminer si du lait ou du thé avait été versé en premier dans une tasse, uniquement à partir du goût. Dans le cadre de l'expérience, Fisher a disposé huit tasses et lui a demandé d'identifier celles qui contenaient « d'abord du lait » et celles qui contenaient « d'abord du thé ». En raison de la petite taille de l'échantillon, Fisher a développé une méthode exacte pour déterminer si le schéma des réponses correctes pouvait être le fruit du hasard, jetant ainsi les bases de ce que nous appelons aujourd'hui le test exact de Fisher.

Dans les situations où les données sont limitées, déséquilibrées ou difficiles à obtenir, comme dans la recherche clinique, le test de Fisher permet de déterminer si les traitements et les résultats sont associés de manière significative. L'écologie, l'épidémiologie, la génétique et le contrôle qualité sont quelques-uns des domaines qui impliquent des données éparses et s'appuient sur ce test.

Le test exact de Fisher évalue l'indépendance en calculantdes probabilités hypergéométriques exactes. Pour un tableau 2×2 :

La probabilité d'observer cetteconfiguration exacte sous l'hypothèse nulle (aucune association) est calculée à l'aide de la distribution hypergéométrique :

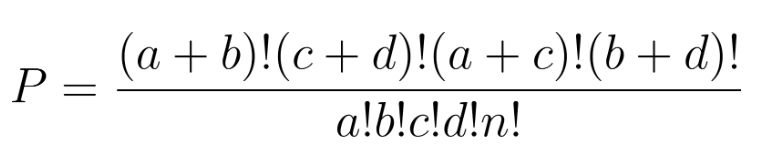
Les tests peuvent être unilatéraux, par exemple en répondant à la question « A1 est-il plus probable dans B1 que dans B2 ? », ou bilatéraux : « Y a-t-il un lien quelconque ? » Contrairement aux approximations sur de grands échantillons (par exemple, le chi carré), la méthode de Fisher garantit la précision même lorsque les fréquences attendues sont faibles.

Hypothèses et conditions préalables

Pour appliquer le test exact de Fisher, les conditions suivantes doivent être remplies.

• Les données doivent être catégoriques.
• Présenté dans un tableau de contingence 2×2
• Les observations sont indépendantes
• Les marges (totaux des lignes et des colonnes) sont fixées sous la valeur nulle.

Le test de Fisher est préférable lorsque l'un des nombres attendus dans la grille est extrêmement faible (inférieur à 5) ou lorsque les résultats sont clairsemés ou fortement déséquilibrés.

Test exact de Fisher en Python

Supposons que nous évaluions si un médicamentaméliore la guérison :

Voici les hypothèses :

• H₀ : Le traitement et le rétablissement sont indépendants
• H₁ : Le traitement favorise le rétablissement (unilatéral)

Et voici comment j'envisagerais cela en Python :

from scipy.stats import fisher_exact

# Construct contingency table
table = [[8, 2],
         [4, 11]]

oddsratio, p_value = fisher_exact(table, alternative='two-sided')
print("Odds Ratio:", oddsratio)
print("Two-sided p-value:", round(p_value, 2))

# One-sided test (treatment better)
_, p_value_one = fisher_exact(table, alternative='greater')
print("One-sided p-value:", round(p_value_one, 2))

Odds Ratio: 11.0
Two-sided p-value: 0.02
One-sided p-value: 0.01

Une valeur p faible de 0,02 suggère une association réelle entre le traitement et la guérison.

Maintenant, prenons un exemple concret à partir des données publiques NHANES 2017-2018 pour examiner le lien entre le « statut tabagique actuel » et le fait d'avoir « déjà reçu un diagnostic d'asthme » chez les adultes.

Fichiers utilisés (tous provenant du site officiel du NHANES) :

• DEMO_J.XPT — Données démographiques (âge, sexe, poids, etc.)

• SMQ_J.XPT — Tabagisme - Consommation de cigarettes (antécédents de tabagisme et consommation actuelle)

• MCQ_J.XPT — Problèmes de santé (y compris « avez-vous déjà été diagnostiqué comme asthmatique »)

Voici les étapes que nous allons suivre :

1. Veuillez télécharger et charger les ensembles de données.

2. Créer des variables binaires :

1. current_smoker (oui/non)

2. asthma_ever (oui/non)

3. Construisez un tableau de contingence 2×2.

4. Effectuer le test exact de Fisher (bilatéral et unilatéral)

5. Calculez un intervalle de confiance à 95 % pour le rapport de cotes.

6. Interpréter les résultats

Remarque: Une analyse NHANES adéquate nécessite des pondérations d'enquête et une conception complexe.

Dans ce cas, nous ne tenons pas compte des pondérations à des fins didactiques. Veuillez importer les bibliothèques requises.

# %% Imports
import pandas as pd
import numpy as np
from scipy.stats import fisher_exact
from statsmodels.stats.contingency_tables import Table2x2

Veuillez télécharger manuellement les fichiers XPT depuis CDC et les placer dans un dossier local nommé data/:

• Veuillez vous rendre à :

• Données démographiques : Données démographiques 2017-2018 (DEMO_J)

• Conditions médicales : MCQ_J

• Tabagisme - Consommation de cigarettes : SMQ_J

• Télécharger :

• DEMO_J Data [XPT]

• MCQ_J Data [XPT]

• SMQ_J Data [XPT]

• Veuillez les enregistrer sous :

• data/DEMO_J.XPT

• data/MCQ_J.XPT

• data/SMQ_J.XPT

# Set paths or URLs here.
# If you've downloaded locally, point to the local paths:
DEMO_PATH = "data/DEMO_J.XPT"
MCQ_PATH  = "data/MCQ_J.XPT"
SMQ_PATH  = "data/SMQ_J.XPT"

# If you prefer to read directly from URLs, uncomment these instead:
# DEMO_PATH = "https://wwwn.cdc.gov/Nchs/NHanes/2017-2018/DEMO_J.XPT"
# MCQ_PATH  = "https://wwwn.cdc.gov/Nchs/NHanes/2017-2018/MCQ_J.XPT"
# SMQ_PATH  = "https://wwwn.cdc.gov/Nchs/NHanes/2017-2018/SMQ_J.XPT"

# Read SAS transport (.XPT) files
demo = pd.read_sas(DEMO_PATH, format="xport")
mcq  = pd.read_sas(MCQ_PATH,  format="xport")
smq  = pd.read_sas(SMQ_PATH,  format="xport")

demo.head()

mcq.head()

smq.head()

Examinons quelques variables clés dans ces DataFrames. Ici, SEQN est l'identifiant du répondant et peut être utilisé comme clé de jointure.

# %% Inspect key variables

# SEQN is the respondent ID present in all three files.
# Check columns and pick what we need:
print("DEMO columns (subset):", demo.columns[:10])
print("MCQ columns (subset):", mcq.columns[:10])
print("SMQ columns (subset):", smq.columns[:10])

DEMO columns (subset): Index(['SEQN', 'SDDSRVYR', 'RIDSTATR', 'RIAGENDR', 'RIDAGEYR', 'RIDAGEMN',
       'RIDRETH1', 'RIDRETH3', 'RIDEXMON', 'RIDEXAGM'],
      dtype='object')
MCQ columns (subset): Index(['SEQN', 'MCQ010', 'MCQ025', 'MCQ035', 'MCQ040', 'MCQ050', 'AGQ030',
       'MCQ053', 'MCQ080', 'MCQ092'],
      dtype='object')
SMQ columns (subset): Index(['SEQN', 'SMQ020', 'SMD030', 'SMQ040', 'SMQ050Q', 'SMQ050U', 'SMD057',
       'SMQ078', 'SMD641', 'SMD650'],
      dtype='object')

Veuillez filtrer les colonnes requises et également filtrer par âge (supérieur à 20 ans). 

# %% Keep only necessary variables and filter adults

demo_sub = demo[["SEQN", "RIDAGEYR", "RIAGENDR"]].copy()
mcq_sub  = mcq[["SEQN", "MCQ010"]].copy()
smq_sub  = smq[["SEQN", "SMQ040"]].copy()

# Merge on SEQN (inner join: keep only participants present in all three files)
df = (
    demo_sub
    .merge(mcq_sub, on="SEQN", how="inner")
    .merge(smq_sub, on="SEQN", how="inner")
)
# Restrict to adults aged 20+
df = df[df["RIDAGEYR"] >= 20].copy()
df.head()

MCQ010 représente les patients souffrant d'asthme, où la valeur « 1 » correspond à « Oui » et « 2 » à « Non ». De même, « SMQ040 » indique si le répondant est fumeur ou non. 

# %% Recode variables into binary indicators

# 1. Asthma: MCQ010
#    1 = Yes, 2 = No, 7 = Refused, 9 = Don't know
#    We'll create asthma_ever: 1 = yes, 0 = no, NaN otherwise

df["asthma_ever"] = np.nan
df.loc[df["MCQ010"] == 1, "asthma_ever"] = 1
df.loc[df["MCQ010"] == 2, "asthma_ever"] = 0

# 2. Current smoker: SMQ040
#    1 = Every day, 2 = Some days, 3 = Not at all, 7/9 = missing
#    We'll create current_smoker: 1 = yes (1 or 2), 0 = no (3), NaN otherwise

df["current_smoker"] = np.nan
df.loc[df["SMQ040"].isin([1, 2]), "current_smoker"] = 1
df.loc[df["SMQ040"] == 3, "current_smoker"] = 0

# Drop rows with missing recodes
df_clean = df.dropna(subset=["asthma_ever", "current_smoker"]).copy()
df_clean[["RIDAGEYR", "MCQ010", "asthma_ever", "SMQ040", "current_smoker"]].head()

Nous créons de nouvelles colonnes, asthma_ever et current_smoker

Veuillez créer le tableau de contingence afin que nous puissions utiliser le test exact de Fisher.

# %% Build a 2×2 contingency table

# Ensure ints
df_clean["asthma_ever"] = df_clean["asthma_ever"].astype(int)
df_clean["current_smoker"] = df_clean["current_smoker"].astype(int)

contingency = pd.crosstab(
    df_clean["current_smoker"],
    df_clean["asthma_ever"],
    rownames=["Current smoker (1=yes,0=no)"],
    colnames=["Ever told asthma (1=yes,0=no)"]
)
contingency

Convertissez le tableau de contingence en un tableau NumPy.

# %% Fisher's Exact Test

# Convert to 2x2 numpy array with explicit ordering:
# rows: [non-smoker, smoker] ; cols: [no asthma, asthma]
table = np.array([
    [contingency.loc[0, 0], contingency.loc[0, 1]],
    [contingency.loc[1, 0], contingency.loc[1, 1]]
])

table

array([[1102,  226],
       [ 832,  172]])

Enfin, veuillez effectuer les tests exacts de Fisher bilatéraux et unilatéraux.

# Run Fisher's exact test (two-sided and one-sided)
oddsratio, p_two_sided = fisher_exact(table, alternative="two-sided")
_, p_smoker_higher_asthma = fisher_exact(table, alternative="greater")
_, p_smoker_lower_asthma  = fisher_exact(table, alternative="less")

print("2x2 table (rows: non-smoker, smoker; cols: no asthma, asthma)")
print(table)
print()
print(f"Odds ratio (Fisher): {oddsratio:.3f}")
print(f"Two-sided p-value: {p_two_sided:.5f}")
print(f"One-sided p-value (H1: smokers have higher asthma odds): {p_smoker_higher_asthma:.5f}")
print(f"One-sided p-value (H1: smokers have lower asthma odds): {p_smoker_lower_asthma:.5f}")

2x2 table (rows: non-smoker, smoker; cols: no asthma, asthma)
[[1102  226]
 [ 832  172]]

Odds ratio (Fisher): 1.008
Two-sided p-value: 0.95571
One-sided p-value (H1: smokers have higher asthma odds): 0.49274
One-sided p-value (H1: smokers have lower asthma odds): 0.55144

Les valeurs p élevées indiquent qu'il n'existe aucune preuve d'une association statistiquement significative entre le tabagisme actuel et le fait d'avoir déjà reçu un diagnostic d'asthme dans cet échantillon.

Le rapport de cotes ~1 indique que les fumeurs actuels ont pratiquement les mêmes chances que les non-fumeurs de déclarer un diagnostic d'asthme. Toute différence observée s'inscrit largement dans les limites de ce qui pourrait se produire par hasard.

Comparaison avec d'autres méthodes statistiques

Différents tests statistiques sont utilisés pour analyser les relations dans les tableaux de contingence en fonction de la taille de l'échantillon, de la structure des données et des hypothèses :

Test exact de Fisher

Idéal pour les échantillons de petite taille et lorsque le nombre de cellules attendu est faible. Il fournit des valeurs p exactes, ce qui le rend très fiable, mais il peut devenir lent à calculer lorsque les tableaux deviennent volumineux.

Test du chi carré

Le choix standard pour les échantillons de grande taille. Cette méthode est rapide, courante et facile à appliquer, mais elle peut être imprécise lorsque les nombres attendus sont inférieurs à 5, car elle repose sur des approximations.

Test exact de Barnard

Une alternative plus performante au test de Fisher dans les tableaux 2×2. Elle ne suppose pas de marges fixes, ce qui peut rendre les résultats plus sensibles, mais cette méthode est moins largement implémentée dans les logiciels.

Test de McNemar

Conçu pour les données catégorielles appariées ou appariées (par exemple, avant et après traitement chez les mêmes sujets). Il tient compte de la dépendance entre les observations, mais ne peut être utilisé lorsque les points de données sont indépendants.ent.

Considérations relatives au calcul

Les performances peuvent être un sujet de préoccupation avec le test exact de Fisher, car les calculs sont peu efficaces lorsqu'on dépasse les tableaux de contingence simples 2×2. Bien que l'extension Freeman-Halton permette d'appliquer le test à des tableaux 2×3 et 3×3, le coût de calcul augmente rapidement à mesure que la taille du tableau augmente. Par conséquent, les algorithmes efficaces et les optimisations sont particulièrement importants dans des domaines tels que la génétique et la recherche clinique, où des tests précis peuvent devoir être effectués à plusieurs reprises sur de nombreux ensembles de données petits mais complexes.

Interprétation et rapports statistiques

Lors de l'interprétation et de la présentation des résultats du test exact de Fisher, il est important d'inclure la valeur exacte de p, de fournir le rapport de cotes ainsi qu'un intervalle de confiance à 95 %, et d'indiquer clairement si un test unilatéral ou bilatéral a été effectué. Les résultats doivent également être accompagnés d'un contexte pratique afin d'aider les lecteurs à comprendre l'importance concrète des conclusions. Par exemple, on pourrait écrire : Le test exact de Fisher a démontré une association significative entre le traitement et la guérison (OR = 11,0, p = 0,02, bilatéral).

Extensions et applications avancées

Les extensions et les applications avancées du test exact de Fisher permettent de traiter des scénarios de données plus complexes et d'améliorer la précision lors du traitement de petits ensembles de données ou d'ensembles de données clairsemés. L'extension Freeman-Halton permet d'appliquer le test à des tableaux de contingence plus grands que le format standard 2×2, tels que les tableaux 2×3 ou 3×3. Le test exact mid-P offre une alternative moins conservatrice au test de Fisher, améliorant la puissance statistique tout en conservant la fiabilité. Les tests exacts bayésiens intègrent les connaissances préalables dans l'analyse, ce qui les rend particulièrement utiles lorsque les données sont limitées ou lorsque l'avis d'experts peut guider l'inférence. De plus, les méthodes de correction des biais pour les rapports de cotes fournissent des estimations plus précises de la taille de l'effet dans les études portant sur des échantillons de petite taille ou des comptes nuls, ce qui permet une meilleure interprétation de la force et de la direction des associations.

Limites et considérations méthodologiques

Le test exact de Fisher peut être prudent, ce qui peut réduire la puissance statistique et rendre plus difficile la détection des effets réels, en particulier dans les études de petite envergure. Lorsque les données sont très clairsemées, l'interprétation des résultats peut s'avérer difficile, car les intervalles de confiance s'élargissent et les estimations deviennent instables. De plus, l'application répétée du test à de nombreuses variables augmente le risque de fausses découvertes, il est donc important de contrôler soigneusement les tests multiples.

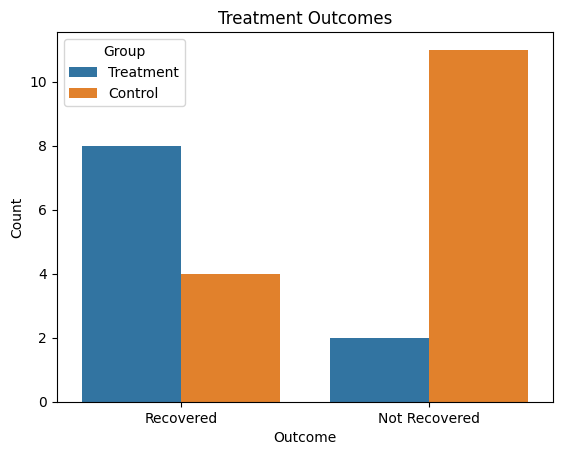
Visualisation des tableaux de contingence

Les options de visualisation appropriées pour présenter les résultats d'un tableau croisé sont les graphiques à barres empilées, les graphiques à barres côte à côte et les graphiques en mosaïque. Ces visuels permettent de communiquer clairement la relation entre les variables catégorielles et facilitent l'interprétation des tendances ou des différences entre les groupes.

Voici un exemple en Python :

import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd

df = pd.DataFrame({
    "Outcome": ["Recovered", "Not Recovered"] * 2,
    "Count": [8, 2, 4, 11],
    "Group": ["Treatment"] * 2 + ["Control"] * 2
})

sns.barplot(data=df, x="Outcome", y="Count", hue="Group")
plt.title("Treatment Outcomes")
plt.show()

Conclusion

Le test exact de Fisher demeure la référence pour l'analyse de petits ensembles de données catégorielles. Né dans une tasse de thé dans un jardin, il est depuis devenu un outil important et largement utilisé en médecine, en génétique, dans la recherche sur les sujets humains et dans l'expérimentation commerciale.

Inscrivez-vous à notre cursus de compétences « Principes fondamentaux des statistiques en Python » pour continuer à vous former. En plus des tests d'hypothèses, ce cursus vous permettra de vous exercer à la construction de modèles statistiques à l'aide de la régression linéaire et logistique.