Exakter Test nach Fisher: Entscheidungen mit kleinen Stichproben treffen

Firmen treffen jeden Tag Entscheidungen, je nachdem, wie sich die Kunden verhalten, wie die Produkte laufen und wie sich der Betrieb verändert. Um sicherzugehen, dass diese Entscheidungen auf echten zugrunde liegenden Beziehungen und Mustern in den Daten basieren, nutzen Analysten oft statistische Tests. 

Während gängige statistische Tests bei großen Datensätzen gut funktionieren, haben Unternehmen nicht immer die Möglichkeit, mit großen Datensätzen zu arbeiten. Tatsächlich müssen viele Entscheidungen anhand kleiner Stichproben, Nischenkundensegmente oder seltener Ereignisse getroffen werden. In solchen Fällen können traditionelle Tests wie der Chi-Quadrat-Test nicht immer das Richtige sein, weil sie entweder irreführende Ergebnisse liefern oder nicht genau genug sind, um die Erkenntnisse sicher umsetzen zu können. 

Hier kommt der exakte Test von Fisher ins Spiel. Lies weiter und ich zeige dir, wie es geht.

Was ist der exakte Test von Fisher?

Der exakte Test von Fisher wird benutzt, um den Zusammenhang zwischen kategorialen Variablen zu checken, wenn die Daten begrenzt sind. Es wird meistens bei 2×2-Kontingenztabellen benutzt und berechnet die genaue Wahrscheinlichkeit, dass man so extreme Daten wie die gesammelten beobachtet, wenn man davon ausgeht, dass die Nullhypothese der Unabhängigkeit stimmt.

Ein Analyst könnte zum Beispiel den exakten Test von Fisher nutzen, um zu checken, wie gut eine gezielte Marketingkampagne funktioniert. Wenn der Analyst zum Beispiel die Wirksamkeit einer E-Mail-Kampagne im Vergleich zu einer Social-Media-Kampagne für eine Nischenkundengruppe mit kleinen Stichprobengrößen testet, könnte er eine Kontingenztafel erstellen und den exakten Test nach Fisher durchführen. Oder in einer Qualitätskontrollumgebung könnte ein Analyst den Test nutzen, um Probleme bei der Meldung von Vorfällen und der Verfolgung von Fehlern anzugehen. Wenn bestimmte Fehlerarten nur selten auftreten, kann man mit dem exakten Test von Fisher herausfinden, ob Faktoren wie der Maschinentyp wirklich mit dem Auftreten von Fehlern zusammenhängen.

Statistische Theorie und mathematische Grundlagen

Nachdem wir ein Gefühl dafür entwickelt haben, warum der Test wichtig ist, können wir ihn jetzt formalisieren. Im Grunde ist der exakte Test von Fisher eine statistische Methode, um zu sehen, ob es einen nicht zufälligen Zusammenhang zwischen zwei kategorialen Variablen gibt. Es wird meistens bei 2×2-Kontingenztabellen benutzt, um zwei Gruppen anhand von zwei Ergebnissen zu vergleichen, zum Beispiel „Behandlung versus Kontrolle“ gegen „verbessert versus nicht verbessert“.

Interessanterweise geht es auf eine der bekanntesten Geschichten in der Statistik zurück, das sogenannte „Lady-Tasting-Tea“-Experiment. Sir Ronald A. Fisher hat ein Experiment entwickelt, um Dr. Muriel Bristols Behauptung, dass sie allein anhand des Geschmacks erkennen könne, ob zuerst Milch oder Tee in eine Tasse gegossen worden sei. Als Teil des Experiments stellte Fisher acht Tassen auf und bat sie, zu sagen, welche „Milch zuerst“ und welche „Tee zuerst“ waren. Wegen der kleinen Stichprobengröße hat Fisher eine genaue Methode entwickelt, um zu checken, ob das Muster der richtigen Vermutungen zufällig entstanden sein könnte. Damit hat er die Basis für das gelegt, was wir heute als Fishers exakter Test kennen.

Wenn Daten knapp, unausgewogen oder schwer zu kriegen sind, wie zum Beispiel in der klinischen Forschung, hilft der Fisher-Test dabei, festzustellen, ob Behandlungen und Ergebnisse in einem sinnvollen Zusammenhang stehen. Ökologie, Epidemiologie, Genetik und Qualitätskontrolle sind ein paar der Bereiche, die mit spärlichen Daten arbeiten und auf diesen Test angewiesen sind.

Der exakte Test von Fisher checkt die Unabhängigkeit, indemer genaue hypergeometrische Wahrscheinlichkeiten berechnet. Für eine 2×2-Tabelle:

Die Wahrscheinlichkeit,genau dieseKonfiguration unter der Nullhypothese (kein Zusammenhang) zu sehen,wird mit der hypergeometrischen Verteilung berechnet:

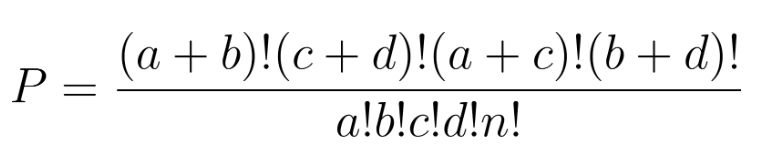
Tests können einseitig sein, wie zum Beispiel die Frage „Ist A1 in B1 wahrscheinlicher als in B2?“ oder zweiseitig: „Irgendeine Verbindung überhaupt?“ Im Gegensatz zu Näherungsverfahren für große Stichproben (z. B. Chi-Quadrat) ist die Methode von Fisher auch dann genau, wenn die erwarteten Häufigkeiten niedrig sind.

Annahmen und Voraussetzungen

Um den exakten Test von Fisher anzuwenden, müssen wir die folgenden Bedingungen erfüllen.

• Die Daten müssen kategorisch sein.
• In einer 2×2-Kontingenztabelle dargestellt
• Die Beobachtungen sind unabhängig voneinander.
• Die Ränder (Zeilen- und Spaltensummen) sind unter Null festgelegt.

Der Fisher-Test ist besser, wenn irgendwelche der erwarteten Werte im Raster extrem niedrig sind (weniger als 5) oder die Ergebnisse spärlich oder stark unausgewogen sind.

Fischers exakter Test in Python

Nehmen wir mal an, wir checken, ob ein Medikamentdie Genesung verbessert:

Hier sind die Hypothesen:

• H₀: Behandlung und Genesung sind voneinander unabhängig.
• H₁: Die Behandlung hilft bei der Genesung (einseitig).

Und so würde ich das in Python machen:

from scipy.stats import fisher_exact

# Construct contingency table
table = [[8, 2],
         [4, 11]]

oddsratio, p_value = fisher_exact(table, alternative='two-sided')
print("Odds Ratio:", oddsratio)
print("Two-sided p-value:", round(p_value, 2))

# One-sided test (treatment better)
_, p_value_one = fisher_exact(table, alternative='greater')
print("One-sided p-value:", round(p_value_one, 2))

Odds Ratio: 11.0
Two-sided p-value: 0.02
One-sided p-value: 0.01

Ein kleiner p-Wert von 0,02 deutet auf einen echten Zusammenhang zwischen Behandlung und Genesung hin.

Nehmen wir jetzt mal ein echtes Beispiel aus den öffentlichen Daten von NHANES 2017–2018, um den Zusammenhang zwischen dem „aktuellen Rauchstatus” und der Angabe „Ihnen wurde jemals gesagt, dass Sie Asthma haben” bei Erwachsenen zu checken.

Verwendete Dateien (alle von der offiziellen NHANES-Website):

• DEMO_J.XPT — Demografische Daten (Alter, Geschlecht, Gewicht usw.)

• SMQ_J.XPT — Rauchen – Zigarettenkonsum (Rauchgewohnheiten in der Vergangenheit und aktuell)

• MCQ_J.XPT — Gesundheitszustand (einschließlich „Wurde dir jemals gesagt, dass du Asthma hast?“)

Hier sind die Schritte, die wir machen werden:

1. Lade die Datensätze runter und mach sie startklar.

2. Binäre Variablen erstellen:

1. current_smoker (ja/nein)

2. asthma_ever (ja/nein)

3. Erstelle eine 2×2-Kontingenz-Tabelle.

4. Mach den exakten Test von Fisher (zweiseitig und einseitig).

5. Berechne ein 95 %-Konfidenzintervall für die Odds Ratio.

6. Die Ergebnisse interpretieren

Anmerkung: Für eine ordentliche NHANES-Analyse braucht man Umfragegewichte und ein kompliziertes Design.

Hier lassen wir Gewichte einfach mal weg, weil es didaktisch sinnvoll ist. Lass uns die benötigten Bibliotheken importieren.

# %% Imports
import pandas as pd
import numpy as np
from scipy.stats import fisher_exact
from statsmodels.stats.contingency_tables import Table2x2

Lass uns die XPT-Dateien manuell von CDC runterladen und in einem lokalen Ordner „ data/ ” ablegen:

• Geh zu:

• Demografie: Bevölkerungsdaten 2017–2018 (DEMO_J)

• Krankheiten: MCQ_J

• Rauchen – Zigarettenkonsum: SMQ_J

• Herunterladen:

• DEMO_J Data [XPT]

• MCQ_J Data [XPT]

• SMQ_J Data [XPT]

• Speichere sie als:

• data/DEMO_J.XPT

• data/MCQ_J.XPT

• data/SMQ_J.XPT

# Set paths or URLs here.
# If you've downloaded locally, point to the local paths:
DEMO_PATH = "data/DEMO_J.XPT"
MCQ_PATH  = "data/MCQ_J.XPT"
SMQ_PATH  = "data/SMQ_J.XPT"

# If you prefer to read directly from URLs, uncomment these instead:
# DEMO_PATH = "https://wwwn.cdc.gov/Nchs/NHanes/2017-2018/DEMO_J.XPT"
# MCQ_PATH  = "https://wwwn.cdc.gov/Nchs/NHanes/2017-2018/MCQ_J.XPT"
# SMQ_PATH  = "https://wwwn.cdc.gov/Nchs/NHanes/2017-2018/SMQ_J.XPT"

# Read SAS transport (.XPT) files
demo = pd.read_sas(DEMO_PATH, format="xport")
mcq  = pd.read_sas(MCQ_PATH,  format="xport")
smq  = pd.read_sas(SMQ_PATH,  format="xport")

demo.head()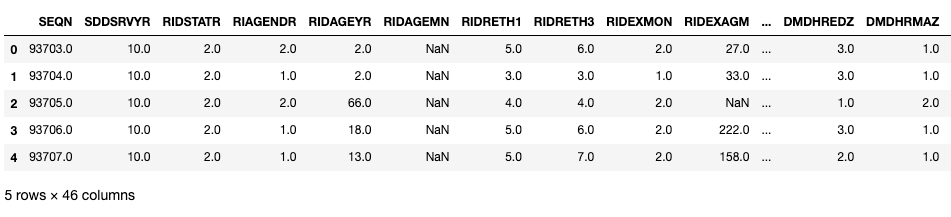

mcq.head()

smq.head()

Schauen wir uns mal ein paar wichtige Variablen in diesen DataFrames an. Hier ist „ SEQN “ die ID des Befragten und kann als Verknüpfungsschlüssel verwendet werden.

# %% Inspect key variables

# SEQN is the respondent ID present in all three files.
# Check columns and pick what we need:
print("DEMO columns (subset):", demo.columns[:10])
print("MCQ columns (subset):", mcq.columns[:10])
print("SMQ columns (subset):", smq.columns[:10])

DEMO columns (subset): Index(['SEQN', 'SDDSRVYR', 'RIDSTATR', 'RIAGENDR', 'RIDAGEYR', 'RIDAGEMN',
       'RIDRETH1', 'RIDRETH3', 'RIDEXMON', 'RIDEXAGM'],
      dtype='object')
MCQ columns (subset): Index(['SEQN', 'MCQ010', 'MCQ025', 'MCQ035', 'MCQ040', 'MCQ050', 'AGQ030',
       'MCQ053', 'MCQ080', 'MCQ092'],
      dtype='object')
SMQ columns (subset): Index(['SEQN', 'SMQ020', 'SMD030', 'SMQ040', 'SMQ050Q', 'SMQ050U', 'SMD057',
       'SMQ078', 'SMD641', 'SMD650'],
      dtype='object')

Lass uns nach den benötigten Spalten filtern und auch nach Alter (älter als 20). 

# %% Keep only necessary variables and filter adults

demo_sub = demo[["SEQN", "RIDAGEYR", "RIAGENDR"]].copy()
mcq_sub  = mcq[["SEQN", "MCQ010"]].copy()
smq_sub  = smq[["SEQN", "SMQ040"]].copy()

# Merge on SEQN (inner join: keep only participants present in all three files)
df = (
    demo_sub
    .merge(mcq_sub, on="SEQN", how="inner")
    .merge(smq_sub, on="SEQN", how="inner")
)
# Restrict to adults aged 20+
df = df[df["RIDAGEYR"] >= 20].copy()
df.head()

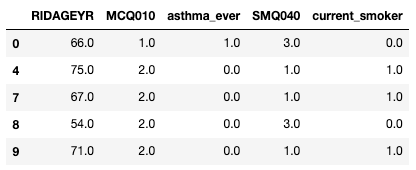
MCQ010 steht für Patienten mit Asthma, wobei der Wert „ 1 ” für „Ja” und „ 2 ” für „Nein” steht. Genauso zeigt „ SMQ040 ”, ob der Befragte Raucher ist oder nicht. 

# %% Recode variables into binary indicators

# 1. Asthma: MCQ010
#    1 = Yes, 2 = No, 7 = Refused, 9 = Don't know
#    We'll create asthma_ever: 1 = yes, 0 = no, NaN otherwise

df["asthma_ever"] = np.nan
df.loc[df["MCQ010"] == 1, "asthma_ever"] = 1
df.loc[df["MCQ010"] == 2, "asthma_ever"] = 0

# 2. Current smoker: SMQ040
#    1 = Every day, 2 = Some days, 3 = Not at all, 7/9 = missing
#    We'll create current_smoker: 1 = yes (1 or 2), 0 = no (3), NaN otherwise

df["current_smoker"] = np.nan
df.loc[df["SMQ040"].isin([1, 2]), "current_smoker"] = 1
df.loc[df["SMQ040"] == 3, "current_smoker"] = 0

# Drop rows with missing recodes
df_clean = df.dropna(subset=["asthma_ever", "current_smoker"]).copy()
df_clean[["RIDAGEYR", "MCQ010", "asthma_ever", "SMQ040", "current_smoker"]].head()

Wir erstellen neue Spalten: „ asthma_ever “ und current_smoker

Lass uns die Kontingenztafel erstellen, damit wir den exakten Test von Fisher verwenden können.

# %% Build a 2×2 contingency table

# Ensure ints
df_clean["asthma_ever"] = df_clean["asthma_ever"].astype(int)
df_clean["current_smoker"] = df_clean["current_smoker"].astype(int)

contingency = pd.crosstab(
    df_clean["current_smoker"],
    df_clean["asthma_ever"],
    rownames=["Current smoker (1=yes,0=no)"],
    colnames=["Ever told asthma (1=yes,0=no)"]
)
contingency

Wandle die Kontingenztafel in ein NumPy-Array um.

# %% Fisher's Exact Test

# Convert to 2x2 numpy array with explicit ordering:
# rows: [non-smoker, smoker] ; cols: [no asthma, asthma]
table = np.array([
    [contingency.loc[0, 0], contingency.loc[0, 1]],
    [contingency.loc[1, 0], contingency.loc[1, 1]]
])

table

array([[1102,  226],
       [ 832,  172]])

Zum Schluss machst du noch den zweiseitigen und den einseitigen exakten Fisher-Test.

# Run Fisher's exact test (two-sided and one-sided)
oddsratio, p_two_sided = fisher_exact(table, alternative="two-sided")
_, p_smoker_higher_asthma = fisher_exact(table, alternative="greater")
_, p_smoker_lower_asthma  = fisher_exact(table, alternative="less")

print("2x2 table (rows: non-smoker, smoker; cols: no asthma, asthma)")
print(table)
print()
print(f"Odds ratio (Fisher): {oddsratio:.3f}")
print(f"Two-sided p-value: {p_two_sided:.5f}")
print(f"One-sided p-value (H1: smokers have higher asthma odds): {p_smoker_higher_asthma:.5f}")
print(f"One-sided p-value (H1: smokers have lower asthma odds): {p_smoker_lower_asthma:.5f}")

2x2 table (rows: non-smoker, smoker; cols: no asthma, asthma)
[[1102  226]
 [ 832  172]]

Odds ratio (Fisher): 1.008
Two-sided p-value: 0.95571
One-sided p-value (H1: smokers have higher asthma odds): 0.49274
One-sided p-value (H1: smokers have lower asthma odds): 0.55144

Hohe p-Werte zeigen, dass es in dieser Stichprobe keinen Beweis für einen statistisch signifikanten Zusammenhang zwischen aktuellem Rauchen und einer jemals diagnostizierten Asthmaerkrankung gibt.

Die Odds Ratio ~1 bedeutet, dass aktuelle Raucher fast genauso oft eine Asthmadiagnose haben wie Nichtraucher. Jeder beobachtete Unterschied liegt weit innerhalb dessen, was durch Zufall auftreten könnte.

Vergleich mit anderen statistischen Methoden

Je nach Stichprobengröße, Datenstruktur und Annahmen werden verschiedene statistische Tests verwendet, um die Beziehungen in Contingenz-Tabellen zu analysieren:

Exakter Test nach Fisher

Am besten für kleine Proben und wenn die erwarteten Zellzahlen niedrig sind. Es liefert genaue p-Werte, was es sehr zuverlässig macht, aber es kann bei großen Tabellen zu einer Verlangsamung der Rechenleistung kommen.

Chi-Quadrat-Test

Die Standardwahl für große Stichproben. Es ist schnell, weit verbreitet und einfach anzuwenden, aber es wird ungenau, wenn die erwarteten Werte unter 5 fallen, weil es auf Schätzungen basiert.

Barnards exakter Test

Eine leistungsstärkere Alternative zum Fisher-Test in 2×2-Tabellen. Es geht nicht von festen Margen aus, was die Ergebnisse empfindlicher machen kann, aber die Methode ist in Software weniger verbreitet.

McNemar-Test

Für gepaarte oder passende kategoriale Daten gemacht (z. B. vor vs. nach der Behandlung bei denselben Probanden). Es berücksichtigt die Abhängigkeit zwischen den Beobachtungen, kann aber nicht verwendet werden, wenn die Datenpunkte unabhängig voneinander sind.ent.

Rechnerische Überlegungen

Die Leistung kann bei Fischers exaktem Test ein Problem sein, weil die Berechnungen bei komplexeren Kontingenztafeln als einfachen 2×2-Tabellen nicht so gut skalieren. Die Freeman-Halton-Erweiterung macht es zwar möglich, den Test auf 2×3- und 3×3-Tabellen anzuwenden, aber die Rechenkosten steigen schnell, wenn die Tabelle größer wird. Deshalb sind effiziente Algorithmen und Optimierungen besonders wichtig in Bereichen wie der Genetik und der klinischen Forschung, wo genaue Tests vielleicht oft an vielen kleinen, aber komplexen Datensätzen durchgeführt werden müssen.

Dolmetschen & statistische Berichterstattung

Bei der Interpretation und Berichterstattung der Ergebnisse des exakten Fisher-Tests ist es wichtig, den genauen p-Wert anzugeben, die Odds Ratio zusammen mit einem 95-prozentigen Konfidenzintervall anzugeben und klar zu sagen, ob ein einseitiger oder zweiseitiger Test durchgeführt wurde. Die Ergebnisse sollten auch mit einem praktischen Kontext untermauert werden, damit die Leser die Bedeutung der Ergebnisse für die Praxis besser verstehen können. Man könnte zum Beispiel schreiben: Der exakte Test von Fisher hat einen deutlichen Zusammenhang zwischen der Behandlung und der Genesung gezeigt (OR=11,0, p=0,02, zweiseitig).

Erweiterungen und fortgeschrittene Anwendungen

Erweiterungen und fortgeschrittene Anwendungen des exakten Tests von Fisher helfen dabei, komplexere Datenszenarien zu bewältigen und die Genauigkeit bei kleinen oder spärlichen Datensätzen zu verbessern. Mit der Freeman-Halton-Erweiterung kann der Test auf größere Kontingenztafeln angewendet werden, die über das Standardformat 2×2 hinausgehen, wie zum Beispiel 2×3- oder 3×3-Tabellen. Der Mid-P-Exakt-Test ist eine weniger konservative Alternative zum Fisher-Test, der die statistische Aussagekraft verbessert und trotzdem zuverlässig bleibt. Bayesianische exakte Tests beziehen Vorwissen in die Analyse mit ein, was sie besonders nützlich macht, wenn die Daten begrenzt sind oder wenn Expertenmeinungen die Schlussfolgerungen beeinflussen können. Außerdem liefern Bias-Korrekturmethoden für Odds Ratios genauere Schätzungen der Effektgröße in Studien mit kleinen Stichproben oder Nullwerten, was eine bessere Interpretation der Stärke und Richtung von Zusammenhängen ermöglicht.

Einschränkungen und methodische Überlegungen

Der exakte Test von Fisher kann konservativ sein, was die statistische Aussagekraft verringern und es schwieriger machen kann, echte Effekte zu erkennen, vor allem bei kleinen Studien. Wenn die Daten echt spärlich sind, kann es schwierig sein, die Ergebnisse zu verstehen, weil die Konfidenzintervalle größer werden und die Schätzungen unzuverlässig werden. Außerdem erhöht die wiederholte Anwendung des Tests auf viele Variablen das Risiko falscher Entdeckungen, weshalb eine sorgfältige Kontrolle bei Mehrfachtests wichtig ist.

Kontingenz-Tabellen anschaulich darstellen

Gute Visualisierungsoptionen für die Darstellung von Kontingenztabellen-Ergebnissen sind gestapelte Balkendiagramme, nebeneinander angeordnete Balkendiagramme und Mosaikdiagramme. Diese Bilder helfen dabei, die Beziehung zwischen kategorialen Variablen klar zu zeigen und Muster oder Gruppenunterschiede einfacher zu verstehen.

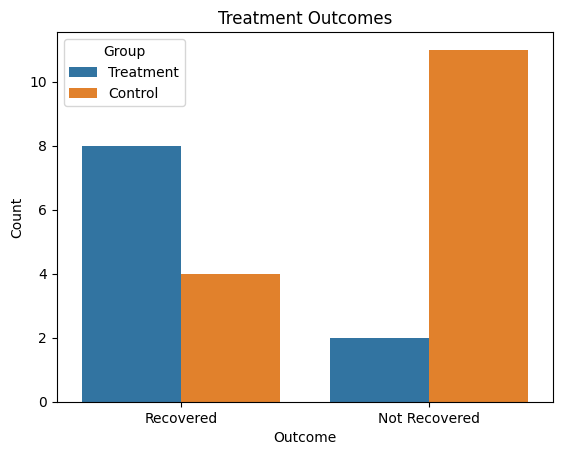
Hier ist ein Beispiel in Python:

import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd

df = pd.DataFrame({
    "Outcome": ["Recovered", "Not Recovered"] * 2,
    "Count": [8, 2, 4, 11],
    "Group": ["Treatment"] * 2 + ["Control"] * 2
})

sns.barplot(data=df, x="Outcome", y="Count", hue="Group")
plt.title("Treatment Outcomes")
plt.show()

Fazit

Der exakte Test von Fisher ist immer noch der Goldstandard für die Analyse kleiner kategorialer Datensätze. Es hat sich von einer Teetasse in einem Garten zu einem wichtigen und weit verbreiteten Werkzeug in der Medizin, Genetik, Forschung am Menschen und in der Wirtschaft entwickelt.

Mach bei unserem Lernpfad „Statistik-Grundlagen in Python“ mit, um weiterzulernen. Da lernst du nicht nur was über Hypothesentests, sondern kannst auch das Erstellen statistischer Modelle mit linearer und logistischer Regression üben.