Prueba exacta de Fisher: Tomar decisiones con muestras pequeñas

Las organizaciones toman decisiones a diario basándose en el comportamiento de los clientes, el rendimiento de los productos y las fluctuaciones en las operaciones. Para garantizar que estas decisiones se basen en relaciones y patrones subyacentes genuinos en los datos, los analistas suelen utilizar pruebas estadísticas. 

Aunque las pruebas estadísticas comunes funcionan bien con conjuntos de datos grandes, las empresas no siempre tienen el lujo de trabajar con conjuntos de datos grandes. De hecho, muchas decisiones deben tomarse utilizando muestras de tamaño reducido, segmentos de clientes muy específicos o acontecimientos poco frecuentes. En estas situaciones, las pruebas tradicionales, como la chi-cuadrado, pueden resultar insuficientes, ya sea porque producen resultados engañosos o porque carecen de la precisión necesaria para actuar con confianza sobre la base de los conocimientos obtenidos. 

Aquí es donde la prueba exacta de Fisher cobra valor. Sigue leyendo y te mostraré cómo hacerlo.

¿Qué es la prueba exacta de Fisher?

La prueba exacta de Fisher se utiliza para evaluar la asociación entre variables categóricas cuando los datos son limitados. Se aplica con mayor frecuencia a 2×2 tablas de contingencia y calcula la probabilidad exacta de observar datos tan extremos como los recopilados, suponiendo que la hipótesis nula de independencia sea cierta.

Un analista podría utilizar la prueba exacta de Fisher, por ejemplo, al evaluar la eficacia de una campaña de marketing dirigida. Si, por ejemplo, el analista estuviera evaluando la eficacia de un correo electrónico frente a una campaña en redes sociales, y esto fuera para un grupo de clientes muy específico con muestras de tamaño reducido, podría crear una tabla de contingencia y realizar la prueba exacta de Fisher. O bien, en un entorno de control de calidad, un analista podría utilizar la prueba para abordar los retos que plantean la notificación de incidentes y el seguimiento de defectos. Cuando ciertos tipos de fallos solo se producen en contadas ocasiones, la prueba exacta de Fisher permite evaluar si factores como el tipo de máquina están realmente relacionados con la aparición de defectos.

Teoría estadística y fundamentos matemáticos

Una vez que hemos desarrollado un sentido intuitivo de por qué la prueba es importante, ahora podemos formalizarlo. En esencia, la prueba exacta de Fisher es un método estadístico que se utiliza para determinar si existe una asociación no aleatoria entre dos variables categóricas. Se aplica con mayor frecuencia a 2×2 tablas de contingencia para comparar dos grupos en función de dos resultados, por ejemplo, «tratamiento frente a control» frente a «mejora frente a sin mejora».

Curiosamente, sus orígenes se remontan a una de las historias más famosas de la estadística, conocida como el experimento de «la dama que degusta el té». Sir Ronald A. Fisher diseñó un experimento para evaluar al Dr. La afirmación de Muriel Bristol de que podía distinguir si se había vertido primero leche o té en una taza únicamente por el sabor. Como parte del experimento, Fisher colocó ocho tazas y te pidió que identificaras cuáles eran «primero leche» y cuáles «primero té». Debido al reducido tamaño de la muestra, Fisher desarrolló un método exacto para determinar si el patrón de aciertos podía haberse producido por casualidad, sentando así las bases de lo que hoy conocemos como prueba exacta de Fisher.

En situaciones en las que los datos son limitados, desequilibrados o difíciles de obtener, como en la investigación clínica, la prueba de Fisher ayuda a determinar si los tratamientos y los resultados están asociados de manera significativa. La ecología, la epidemiología, la genética y el control de calidad son algunos de los campos que implican datos escasos y dependen de esta prueba.

La prueba exacta de Fisher evalúa la independencia calculandoprobabilidades hipergeométricas exactas. Para una tabla de 2×2:

La probabilidad de observar esaconfiguración exacta bajo la hipótesis nula (sin asociación) se calcula con la distribución hipergeométrica:

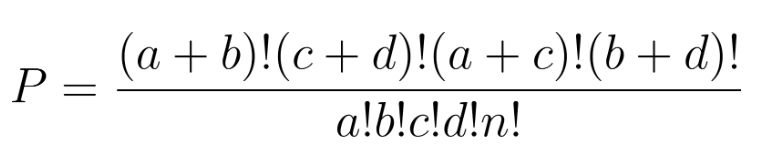
Las pruebas pueden ser unilaterales, como responder «¿Es más probable que A1 se dé en B1 que en B2?», o bilaterales: ¿Alguna asociación? A diferencia de las aproximaciones con muestras grandes (por ejemplo, la chi cuadrado), el método de Fisher garantiza la precisión incluso cuando las frecuencias esperadas son bajas.

Supuestos y requisitos previos

Para aplicar la prueba exacta de Fisher, necesitamos que se den las siguientes condiciones.

• Los datos deben ser categóricos.
• Presentado en una tabla de contingencia 2×2.
• Las observaciones son independientes.
• Los márgenes (totales de filas y columnas) se fijan bajo el valor nulo.

La prueba de Fisher es preferible cuando cualquiera de los recuentos esperados en la parilla es extremadamente bajo (menos de 5) o cuando los resultados son escasos o muy desequilibrados.

Prueba exacta de Fisher en Python

Supongamos que probamos si un medicamentomejora la recuperación:

Estas son las hipótesis:

• H₀: El tratamiento y la recuperación son independientes.
• H₁: El tratamiento mejora la recuperación (unilateral).

Y así es como lo consideraría en Python:

from scipy.stats import fisher_exact

# Construct contingency table
table = [[8, 2],
         [4, 11]]

oddsratio, p_value = fisher_exact(table, alternative='two-sided')
print("Odds Ratio:", oddsratio)
print("Two-sided p-value:", round(p_value, 2))

# One-sided test (treatment better)
_, p_value_one = fisher_exact(table, alternative='greater')
print("One-sided p-value:", round(p_value_one, 2))

Odds Ratio: 11.0
Two-sided p-value: 0.02
One-sided p-value: 0.01

Un valor p pequeño, de 0,02, sugiere una asociación real entre el tratamiento y la recuperación.

Ahora, tomemos un ejemplo real utilizando los datos públicos de NHANES 2017-2018 para examinar la asociación entre «el estado actual de tabaquismo» y «si alguna vez te han dicho que tienes asma» en adultos.

Archivos utilizados (todos procedentes del sitio web oficial de NHANES):

• DEMO_J.XPT — Datos demográficos (edad, sexo, peso, etc.)

• SMQ_J.XPT — Tabaquismo: consumo de cigarrillos (historial de tabaquismo y consumo actual).

• MCQ_J.XPT — Afecciones médicas (incluido «si alguna vez te han dicho que tienes asma»)

A continuación, se detallan los pasos que vamos a seguir:

1. Descargar y cargar los conjuntos de datos

2. Crear variables binarias:

1. current_smoker (sí/no)

2. asthma_ever (sí/no)

3. Crea una tabla de contingencia 2×2.

4. Ejecuta la prueba exacta de Fisher (bilateral y unilateral).

5. Calcula un intervalo de confianza del 95 % para la razón de probabilidades.

6. Interpreta los resultados.

Nota: Un análisis adecuado de NHANES requiere ponderaciones de la encuesta y un diseño complejo.

Aquí, ignoramos los pesos con fines didácticos. Importemos las bibliotecas necesarias.

# %% Imports
import pandas as pd
import numpy as np
from scipy.stats import fisher_exact
from statsmodels.stats.contingency_tables import Table2x2

Descarguen manualmente los archivos XPT de CDC y colóquenlos en una carpeta local data/:

• Ir a:

• Datos demográficos: 2017–2018 Demographics Data (DEMO_J)

• Afecciones médicas: MCQ_J

• Tabaquismo - Consumo de cigarrillos: SMQ_J

• Descargar:

• DEMO_J Data [XPT]

• MCQ_J Data [XPT]

• SMQ_J Data [XPT]

• Guárdalos como:

• data/DEMO_J.XPT

• data/MCQ_J.XPT

• data/SMQ_J.XPT

# Set paths or URLs here.
# If you've downloaded locally, point to the local paths:
DEMO_PATH = "data/DEMO_J.XPT"
MCQ_PATH  = "data/MCQ_J.XPT"
SMQ_PATH  = "data/SMQ_J.XPT"

# If you prefer to read directly from URLs, uncomment these instead:
# DEMO_PATH = "https://wwwn.cdc.gov/Nchs/NHanes/2017-2018/DEMO_J.XPT"
# MCQ_PATH  = "https://wwwn.cdc.gov/Nchs/NHanes/2017-2018/MCQ_J.XPT"
# SMQ_PATH  = "https://wwwn.cdc.gov/Nchs/NHanes/2017-2018/SMQ_J.XPT"

# Read SAS transport (.XPT) files
demo = pd.read_sas(DEMO_PATH, format="xport")
mcq  = pd.read_sas(MCQ_PATH,  format="xport")
smq  = pd.read_sas(SMQ_PATH,  format="xport")

demo.head()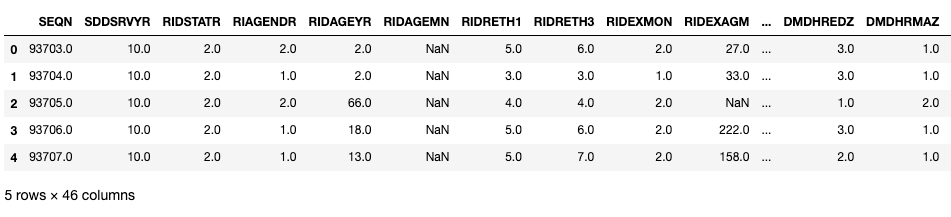

mcq.head()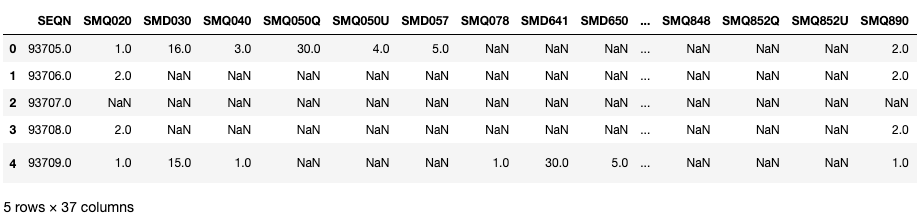

smq.head()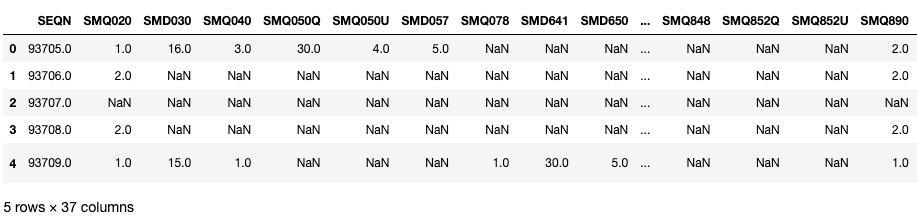

Veamos algunas variables clave en estos DataFrames. Aquí, SEQN es el ID del encuestado y se puede utilizar como clave de unión.

# %% Inspect key variables

# SEQN is the respondent ID present in all three files.
# Check columns and pick what we need:
print("DEMO columns (subset):", demo.columns[:10])
print("MCQ columns (subset):", mcq.columns[:10])
print("SMQ columns (subset):", smq.columns[:10])

DEMO columns (subset): Index(['SEQN', 'SDDSRVYR', 'RIDSTATR', 'RIAGENDR', 'RIDAGEYR', 'RIDAGEMN',
       'RIDRETH1', 'RIDRETH3', 'RIDEXMON', 'RIDEXAGM'],
      dtype='object')
MCQ columns (subset): Index(['SEQN', 'MCQ010', 'MCQ025', 'MCQ035', 'MCQ040', 'MCQ050', 'AGQ030',
       'MCQ053', 'MCQ080', 'MCQ092'],
      dtype='object')
SMQ columns (subset): Index(['SEQN', 'SMQ020', 'SMD030', 'SMQ040', 'SMQ050Q', 'SMQ050U', 'SMD057',
       'SMQ078', 'SMD641', 'SMD650'],
      dtype='object')

Filtremos las columnas necesarias y también por edad (mayor de 20). 

# %% Keep only necessary variables and filter adults

demo_sub = demo[["SEQN", "RIDAGEYR", "RIAGENDR"]].copy()
mcq_sub  = mcq[["SEQN", "MCQ010"]].copy()
smq_sub  = smq[["SEQN", "SMQ040"]].copy()

# Merge on SEQN (inner join: keep only participants present in all three files)
df = (
    demo_sub
    .merge(mcq_sub, on="SEQN", how="inner")
    .merge(smq_sub, on="SEQN", how="inner")
)
# Restrict to adults aged 20+
df = df[df["RIDAGEYR"] >= 20].copy()
df.head()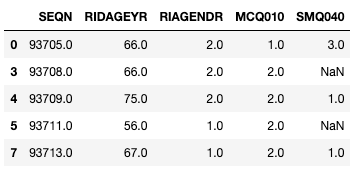

MCQ010 representa a pacientes con asma, donde el valor de « 1 » es «Yes» y « 2 » significa «No». Del mismo modo, « SMQ040 » indica si el encuestado es fumador o no. 

# %% Recode variables into binary indicators

# 1. Asthma: MCQ010
#    1 = Yes, 2 = No, 7 = Refused, 9 = Don't know
#    We'll create asthma_ever: 1 = yes, 0 = no, NaN otherwise

df["asthma_ever"] = np.nan
df.loc[df["MCQ010"] == 1, "asthma_ever"] = 1
df.loc[df["MCQ010"] == 2, "asthma_ever"] = 0

# 2. Current smoker: SMQ040
#    1 = Every day, 2 = Some days, 3 = Not at all, 7/9 = missing
#    We'll create current_smoker: 1 = yes (1 or 2), 0 = no (3), NaN otherwise

df["current_smoker"] = np.nan
df.loc[df["SMQ040"].isin([1, 2]), "current_smoker"] = 1
df.loc[df["SMQ040"] == 3, "current_smoker"] = 0

# Drop rows with missing recodes
df_clean = df.dropna(subset=["asthma_ever", "current_smoker"]).copy()
df_clean[["RIDAGEYR", "MCQ010", "asthma_ever", "SMQ040", "current_smoker"]].head()

Creamos nuevas columnas, asthma_ever y current_smoker

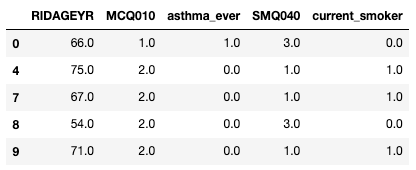
Creemos la tabla de contingencia para poder utilizar la prueba exacta de Fisher.

# %% Build a 2×2 contingency table

# Ensure ints
df_clean["asthma_ever"] = df_clean["asthma_ever"].astype(int)
df_clean["current_smoker"] = df_clean["current_smoker"].astype(int)

contingency = pd.crosstab(
    df_clean["current_smoker"],
    df_clean["asthma_ever"],
    rownames=["Current smoker (1=yes,0=no)"],
    colnames=["Ever told asthma (1=yes,0=no)"]
)
contingency

Convierte la tabla de contingencia en un arreglo NumPy.

# %% Fisher's Exact Test

# Convert to 2x2 numpy array with explicit ordering:
# rows: [non-smoker, smoker] ; cols: [no asthma, asthma]
table = np.array([
    [contingency.loc[0, 0], contingency.loc[0, 1]],
    [contingency.loc[1, 0], contingency.loc[1, 1]]
])

table

array([[1102,  226],
       [ 832,  172]])

Por último, ejecuta pruebas exactas de Fisher bilaterales y unilaterales.

# Run Fisher's exact test (two-sided and one-sided)
oddsratio, p_two_sided = fisher_exact(table, alternative="two-sided")
_, p_smoker_higher_asthma = fisher_exact(table, alternative="greater")
_, p_smoker_lower_asthma  = fisher_exact(table, alternative="less")

print("2x2 table (rows: non-smoker, smoker; cols: no asthma, asthma)")
print(table)
print()
print(f"Odds ratio (Fisher): {oddsratio:.3f}")
print(f"Two-sided p-value: {p_two_sided:.5f}")
print(f"One-sided p-value (H1: smokers have higher asthma odds): {p_smoker_higher_asthma:.5f}")
print(f"One-sided p-value (H1: smokers have lower asthma odds): {p_smoker_lower_asthma:.5f}")

2x2 table (rows: non-smoker, smoker; cols: no asthma, asthma)
[[1102  226]
 [ 832  172]]

Odds ratio (Fisher): 1.008
Two-sided p-value: 0.95571
One-sided p-value (H1: smokers have higher asthma odds): 0.49274
One-sided p-value (H1: smokers have lower asthma odds): 0.55144

Los valores p elevados muestran que no hay pruebas de una asociación estadísticamente significativa entre el tabaquismo actual y haber sido diagnosticado alguna vez con asma en esta muestra.

La razón de probabilidades ~1 significa que los fumadores actuales tienen prácticamente las mismas probabilidades de informar un diagnóstico de asma que los no fumadores. Cualquier diferencia observada está dentro de lo que podría ocurrir por casualidad.

Comparación con métodos estadísticos alternativos

Se utilizan diferentes pruebas estadísticas para analizar las relaciones en las tablas de contingencia, dependiendo del tamaño de la muestra, la estructura de los datos y las hipótesis:

Prueba exacta de Fisher

Ideal para muestras pequeñas y cuando se esperan recuentos celulares bajos. Proporciona valores p exactos, lo que lo hace muy fiable, pero puede ralentizar los cálculos a medida que las tablas se hacen más grandes.

Prueba de chi cuadrado

La opción estándar para muestras de gran tamaño. Es rápido, habitual y fácil de aplicar, pero resulta inexacto cuando los recuentos esperados son inferiores a 5, debido a que se basa en aproximaciones.

Prueba exacta de Barnard

Una alternativa más potente a la prueba de Fisher en tablas 2×2. No asume márgenes fijos, lo que puede hacer que los resultados sean más sensibles, pero el método está menos implementado en el software.

Prueba de McNemar

Diseñado para datos categóricos emparejados o coincidentes (por ejemplo, antes y después del tratamiento en los mismos sujetos). Tiene en cuenta la dependencia entre observaciones, pero no se puede utilizar cuando los puntos de datos son independientesent.

Consideraciones computacionales

El rendimiento puede ser un problema con la prueba exacta de Fisher, ya que los cálculos se escalan mal cuando se va más allá de las simples tablas de contingencia 2×2. Si bien la extensión de Freeman-Halton permite aplicar la prueba a tablas de 2×3 y 3×3, el coste computacional aumenta rápidamente a medida que crece el tamaño de la tabla. Como resultado, los algoritmos eficientes y las optimizaciones son especialmente importantes en campos como la genética y la investigación clínica, donde puede ser necesario realizar pruebas exactas repetidamente en muchos conjuntos de datos pequeños pero complejos.

Interpretación e informes estadísticos

Al interpretar y comunicar los resultados de la prueba exacta de Fisher, es importante incluir el valor p exacto, proporcionar la razón de probabilidades junto con un intervalo de confianza del 95 % e indicar claramente si se ha realizado una prueba unilateral o bilateral. Los resultados también deben respaldarse con un contexto práctico para ayudar a los lectores a comprender la importancia real de los hallazgos. Por ejemplo, se podría escribir: La prueba exacta de Fisher mostró una asociación significativa entre el tratamiento y la recuperación (OR = 11,0, p = 0,02, bilateral).

Extensiones y aplicaciones avanzadas

Las extensiones y aplicaciones avanzadas de la prueba exacta de Fisher ayudan a abordar escenarios de datos más complejos y a mejorar la precisión cuando se trabaja con conjuntos de datos pequeños o dispersos. La extensión Freeman-Halton permite aplicar la prueba a tablas de contingencia más grandes que el formato estándar 2×2, como las tablas 2×3 o 3×3. La prueba exacta mid-P ofrece una alternativa menos conservadora a la prueba de Fisher, mejorando la potencia estadística y manteniendo al mismo tiempo la fiabilidad. Las pruebas exactas bayesianas incorporan conocimientos previos al análisis, lo que las hace especialmente útiles cuando los datos son limitados o cuando el criterio de los expertos puede orientar la inferencia. Además, los métodos de corrección del sesgo para las odds ratio proporcionan estimaciones más precisas del tamaño del efecto en estudios con muestras pequeñas o recuentos nulos, lo que garantiza una mejor interpretación de la fuerza y la dirección de las asociaciones.

Limitaciones y consideraciones metodológicas

La prueba exacta de Fisher puede ser conservadora, lo que puede reducir la potencia estadística y dificultar la detección de efectos reales, especialmente en estudios pequeños. Cuando los datos son muy escasos, interpretar los resultados puede resultar complicado, ya que los intervalos de confianza se amplían y las estimaciones se vuelven inestables. Además, aplicar la prueba repetidamente en muchas variables aumenta el riesgo de descubrimientos falsos, por lo que es importante controlar cuidadosamente las pruebas múltiples.

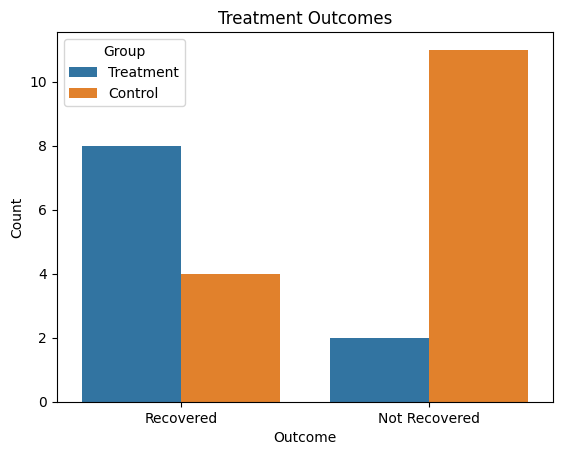
Visualización de tablas de contingencia

Las buenas opciones de visualización para presentar los resultados de las tablas de contingencia incluyen gráficos de barras apiladas, gráficos de barras en paralelo y gráficos de mosaico. Estas imágenes ayudan a comunicar claramente la relación entre variables categóricas y facilitan la interpretación de patrones o diferencias entre grupos.

Aquí tienes un ejemplo en Python:

import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd

df = pd.DataFrame({
    "Outcome": ["Recovered", "Not Recovered"] * 2,
    "Count": [8, 2, 4, 11],
    "Group": ["Treatment"] * 2 + ["Control"] * 2
})

sns.barplot(data=df, x="Outcome", y="Count", hue="Group")
plt.title("Treatment Outcomes")
plt.show()

Conclusión

La prueba exacta de Fisher sigue siendo el método de referencia para analizar conjuntos de datos categóricos pequeños. Nacido de una taza de té en un jardín, desde entonces ha evolucionado hasta convertirse en una herramienta importante y ampliamente utilizada en medicina, genética, investigación con sujetos humanos y experimentación empresarial.

Inscríbete en nuestro programa de fundamentos de estadística en Python para seguir aprendiendo, que, además de las pruebas de hipótesis, te ayudará a practicar la creación de modelos estadísticos con regresión lineal y logística.