Teste exato de Fisher: Tomando decisões com amostras pequenas

As organizações tomam decisões todos os dias com base no comportamento dos clientes, no desempenho dos produtos e nas flutuações das operações. Para garantir que essas decisões sejam baseadas em relações e padrões reais nos dados, os analistas costumam usar testes estatísticos. 

Embora os testes estatísticos comuns funcionem bem para grandes conjuntos de dados, as empresas nem sempre têm o luxo de trabalhar com grandes conjuntos de dados. Na verdade, muitas decisões precisam ser tomadas usando amostras pequenas, segmentos de clientes específicos ou eventos raros. Nessas situações, testes tradicionais, como o qui-quadrado, podem não ser suficientes, produzindo resultados enganosos ou sem a precisão necessária para agir com confiança com base nas informações obtidas. 

É aí que o teste exato de Fisher se torna útil. Continue lendo e eu vou te mostrar como.

O que é o teste exato de Fisher?

O teste exato de Fisher é usado para avaliar a relação entre variáveis categóricas quando os dados são limitados. É mais frequentemente aplicado a tabelas de contingência 2×2 e calcula a probabilidade exata de observar dados tão extremos quanto os coletados, assumindo que a hipótese nula de independência seja verdadeira.

Um analista pode usar o teste exato de Fisher, por exemplo, ao avaliar a eficácia de uma campanha de marketing direcionada. Se, por exemplo, o analista estivesse testando a eficácia de um e-mail em comparação com uma campanha nas redes sociais, e isso fosse para um grupo específico de clientes com amostras pequenas, ele ou ela poderia criar uma tabela de contingência e fazer o teste exato de Fisher. Ou então, em um ambiente de controle de qualidade, um analista poderia usar o teste para resolver desafios no relatório de incidentes e no rastreamento de defeitos. Quando certos tipos de falhas só acontecem algumas vezes, o teste exato de Fisher pode avaliar se fatores como o tipo de máquina estão realmente ligados à ocorrência de defeitos.

Teoria Estatística e Fundamentos Matemáticos

Depois de entender por que o teste é importante, agora podemos formalizá-lo. Basicamente, o teste exato de Fisher é um método estatístico usado para ver se tem uma relação não aleatória entre duas variáveis categóricas. É mais comumente aplicado a tabelas de contingência 2×2 para comparar dois grupos em dois resultados, por exemplo, “tratamento versus controle” contra “melhoria versus sem melhora”.

Curiosamente, suas origens remontam a uma das histórias mais famosas da estatística, conhecida como o experimento da “senhora provando chá”. Sir Ronald A. Fisher criou um experimento para avaliar o Dr. A Muriel Bristol dizia que conseguia saber se tinha sido derramado leite ou chá primeiro numa chávena só pelo sabor. Como parte do experimento, Fisher arrumou oito xícaras e pediu pra ela identificar quais eram “leite primeiro” e quais eram “chá primeiro”. Por causa do tamanho pequeno da amostra, Fisher criou um jeito exato de ver se o padrão de respostas certas poderia ter rolado por acaso, criando a base do que hoje conhecemos como teste exato de Fisher.

Em situações em que os dados são limitados, desequilibrados ou difíceis de obter, como na pesquisa clínica, o teste de Fisher ajuda a ver se os tratamentos e os resultados estão ligados de um jeito que faz sentido. Ecologia, epidemiologia, genética e controle de qualidade são algumas das áreas que lidam com dados escassos e dependem desse teste.

O teste exato de Fisher avalia a independência calculandoprobabilidades hipergeométricas exatas. Para uma tabela 2×2:

A chance de ver essaconfiguração exata na hipótese nula (sem associação) é calculada com a distribuição hipergeométrica:

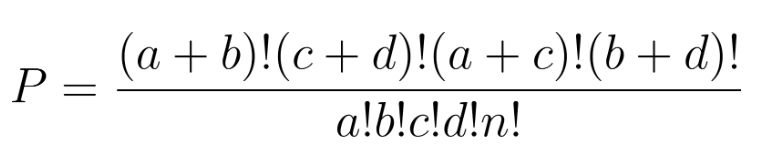
Os testes podem ser unilaterais, como responder “A1 é mais provável em B1 do que em B2?” ou bilaterais: “Alguma associação?” Diferente das aproximações de grandes amostras (por exemplo, qui-quadrado), o método de Fisher garante precisão mesmo quando as frequências esperadas são baixas.

Suposições e pré-requisitos

Para aplicar o teste exato de Fisher, precisamos ter as seguintes condições.

• Os dados têm que ser categóricos.
• Apresentado em uma tabela de contingência 2×2
• As observações são independentes
• As margens (totais de linhas e colunas) são fixadas sob o valor nulo.

O teste de Fisher é preferível quando qualquer uma das contagens esperadas na grade é extremamente baixa (menos de 5) ou os resultados são escassos ou muito desequilibrados.

Teste exato de Fisher em Python

Digamos que a gente teste se um remédioajuda na recuperação:

Aqui estão as hipóteses:

• H₀: O tratamento e a recuperação são independentes.
• H₁: O tratamento melhora a recuperação (unilateral)

E aqui está como eu consideraria isso em Python:

from scipy.stats import fisher_exact

# Construct contingency table
table = [[8, 2],
         [4, 11]]

oddsratio, p_value = fisher_exact(table, alternative='two-sided')
print("Odds Ratio:", oddsratio)
print("Two-sided p-value:", round(p_value, 2))

# One-sided test (treatment better)
_, p_value_one = fisher_exact(table, alternative='greater')
print("One-sided p-value:", round(p_value_one, 2))

Odds Ratio: 11.0
Two-sided p-value: 0.02
One-sided p-value: 0.01

Um pequeno valor p de 0,02 sugere uma associação real entre o tratamento e a recuperação.

Agora, vamos pegar um exemplo da vida real usando dados públicos do NHANES 2017–2018 para ver a relação entre “status atual de tabagismo” e “já ter sido diagnosticado com asma” em adultos.

Arquivos usados (todos do site oficial do NHANES):

• DEMO_J.XPT — Dados demográficos (idade, sexo, peso, etc.)

• SMQ_J.XPT — Tabagismo - Uso de cigarros (histórico de tabagismo e uso atual)

• MCQ_J.XPT — Condições médicas (incluindo “já lhe disseram que você tem asma”)

Aqui estão os passos que vamos seguir:

1. Baixe e carregue os conjuntos de dados

2. Crie variáveis binárias:

1. current_smoker (sim/não)

2. asthma_ever (sim/não)

3. Crie uma tabela de contingência 2×2

4. Execute o teste exato de Fisher (bilateral e unilateral)

5. Calcule um intervalo de confiança de 95% para a razão de chances.

6. Interprete os resultados

Observação: Uma análise NHANES adequada precisa de pesos de pesquisa e um projeto complexo.

Aqui, a gente ignora os pesos por motivos didáticos. Vamos importar as bibliotecas necessárias.

# %% Imports
import pandas as pd
import numpy as np
from scipy.stats import fisher_exact
from statsmodels.stats.contingency_tables import Table2x2

Vamos baixar manualmente os arquivos XPT do CDC e colocá-los em uma pasta local chamada data/:

• Vá para:

• Dados demográficos: Dados demográficos de 2017–2018 (DEMO_J)

• Condições médicas: MCQ_J

• Fumar - Uso de cigarros: SMQ_J

• Baixar:

• DEMO_J Data [XPT]

• MCQ_J Data [XPT]

• Dados SMQ_J [XPT]

• Salve-os como:

• data/DEMO_J.XPT

• data/MCQ_J.XPT

• data/SMQ_J.XPT

# Set paths or URLs here.
# If you've downloaded locally, point to the local paths:
DEMO_PATH = "data/DEMO_J.XPT"
MCQ_PATH  = "data/MCQ_J.XPT"
SMQ_PATH  = "data/SMQ_J.XPT"

# If you prefer to read directly from URLs, uncomment these instead:
# DEMO_PATH = "https://wwwn.cdc.gov/Nchs/NHanes/2017-2018/DEMO_J.XPT"
# MCQ_PATH  = "https://wwwn.cdc.gov/Nchs/NHanes/2017-2018/MCQ_J.XPT"
# SMQ_PATH  = "https://wwwn.cdc.gov/Nchs/NHanes/2017-2018/SMQ_J.XPT"

# Read SAS transport (.XPT) files
demo = pd.read_sas(DEMO_PATH, format="xport")
mcq  = pd.read_sas(MCQ_PATH,  format="xport")
smq  = pd.read_sas(SMQ_PATH,  format="xport")

demo.head()

mcq.head()

smq.head()

Vamos dar uma olhada em algumas variáveis importantes nesses DataFrames. Aqui, SEQN é o ID do respondente e pode ser usado como uma chave de junção.

# %% Inspect key variables

# SEQN is the respondent ID present in all three files.
# Check columns and pick what we need:
print("DEMO columns (subset):", demo.columns[:10])
print("MCQ columns (subset):", mcq.columns[:10])
print("SMQ columns (subset):", smq.columns[:10])

DEMO columns (subset): Index(['SEQN', 'SDDSRVYR', 'RIDSTATR', 'RIAGENDR', 'RIDAGEYR', 'RIDAGEMN',
       'RIDRETH1', 'RIDRETH3', 'RIDEXMON', 'RIDEXAGM'],
      dtype='object')
MCQ columns (subset): Index(['SEQN', 'MCQ010', 'MCQ025', 'MCQ035', 'MCQ040', 'MCQ050', 'AGQ030',
       'MCQ053', 'MCQ080', 'MCQ092'],
      dtype='object')
SMQ columns (subset): Index(['SEQN', 'SMQ020', 'SMD030', 'SMQ040', 'SMQ050Q', 'SMQ050U', 'SMD057',
       'SMQ078', 'SMD641', 'SMD650'],
      dtype='object')

Vamos filtrar as colunas necessárias e também filtrar por idade (maior que 20). 

# %% Keep only necessary variables and filter adults

demo_sub = demo[["SEQN", "RIDAGEYR", "RIAGENDR"]].copy()
mcq_sub  = mcq[["SEQN", "MCQ010"]].copy()
smq_sub  = smq[["SEQN", "SMQ040"]].copy()

# Merge on SEQN (inner join: keep only participants present in all three files)
df = (
    demo_sub
    .merge(mcq_sub, on="SEQN", how="inner")
    .merge(smq_sub, on="SEQN", how="inner")
)
# Restrict to adults aged 20+
df = df[df["RIDAGEYR"] >= 20].copy()
df.head()

MCQ010 representa pacientes com asma, onde o valor de 1 é Sim e 2 significa Não. Da mesma forma, SMQ040 mostra se o entrevistado é fumante ou não. 

# %% Recode variables into binary indicators

# 1. Asthma: MCQ010
#    1 = Yes, 2 = No, 7 = Refused, 9 = Don't know
#    We'll create asthma_ever: 1 = yes, 0 = no, NaN otherwise

df["asthma_ever"] = np.nan
df.loc[df["MCQ010"] == 1, "asthma_ever"] = 1
df.loc[df["MCQ010"] == 2, "asthma_ever"] = 0

# 2. Current smoker: SMQ040
#    1 = Every day, 2 = Some days, 3 = Not at all, 7/9 = missing
#    We'll create current_smoker: 1 = yes (1 or 2), 0 = no (3), NaN otherwise

df["current_smoker"] = np.nan
df.loc[df["SMQ040"].isin([1, 2]), "current_smoker"] = 1
df.loc[df["SMQ040"] == 3, "current_smoker"] = 0

# Drop rows with missing recodes
df_clean = df.dropna(subset=["asthma_ever", "current_smoker"]).copy()
df_clean[["RIDAGEYR", "MCQ010", "asthma_ever", "SMQ040", "current_smoker"]].head()

Criamos novas colunas, asthma_ever e current_smoker

Vamos criar a tabela de contingência para que possamos usar o Teste Exato de Fisher.

# %% Build a 2×2 contingency table

# Ensure ints
df_clean["asthma_ever"] = df_clean["asthma_ever"].astype(int)
df_clean["current_smoker"] = df_clean["current_smoker"].astype(int)

contingency = pd.crosstab(
    df_clean["current_smoker"],
    df_clean["asthma_ever"],
    rownames=["Current smoker (1=yes,0=no)"],
    colnames=["Ever told asthma (1=yes,0=no)"]
)
contingency

Transforme a tabela de contingência em uma matriz NumPy.

# %% Fisher's Exact Test

# Convert to 2x2 numpy array with explicit ordering:
# rows: [non-smoker, smoker] ; cols: [no asthma, asthma]
table = np.array([
    [contingency.loc[0, 0], contingency.loc[0, 1]],
    [contingency.loc[1, 0], contingency.loc[1, 1]]
])

table

array([[1102,  226],
       [ 832,  172]])

Por fim, faça os testes exatos de Fisher bilateral e unilateral.

# Run Fisher's exact test (two-sided and one-sided)
oddsratio, p_two_sided = fisher_exact(table, alternative="two-sided")
_, p_smoker_higher_asthma = fisher_exact(table, alternative="greater")
_, p_smoker_lower_asthma  = fisher_exact(table, alternative="less")

print("2x2 table (rows: non-smoker, smoker; cols: no asthma, asthma)")
print(table)
print()
print(f"Odds ratio (Fisher): {oddsratio:.3f}")
print(f"Two-sided p-value: {p_two_sided:.5f}")
print(f"One-sided p-value (H1: smokers have higher asthma odds): {p_smoker_higher_asthma:.5f}")
print(f"One-sided p-value (H1: smokers have lower asthma odds): {p_smoker_lower_asthma:.5f}")

2x2 table (rows: non-smoker, smoker; cols: no asthma, asthma)
[[1102  226]
 [ 832  172]]

Odds ratio (Fisher): 1.008
Two-sided p-value: 0.95571
One-sided p-value (H1: smokers have higher asthma odds): 0.49274
One-sided p-value (H1: smokers have lower asthma odds): 0.55144

Valores elevados de p mostram que não há evidência de uma associação estatisticamente significativa entre o tabagismo atual e o diagnóstico de asma nesta amostra.

A razão de chances ~1 quer dizer que quem fuma hoje tem praticamente as mesmas chances de dizer que tem asma do que quem não fuma. Qualquer diferença observada está bem dentro do que poderia ocorrer por acaso.

Comparando com outros métodos estatísticos

Diferentes testes estatísticos são usados para analisar relações em tabelas de contingência, dependendo do tamanho da amostra, da estrutura dos dados e das suposições:

Teste exato de Fisher

Ideal para amostras pequenas e quando algumas contagens celulares esperadas são baixas. Ele fornece valores p exatos, o que o torna muito confiável, mas pode ficar lento em termos de computação à medida que as tabelas ficam maiores.

Teste do qui-quadrado

A escolha padrão para amostras grandes. É rápido, comum e fácil de aplicar, mas fica impreciso quando as contagens esperadas caem abaixo de 5, porque depende de aproximações.

Teste exato de Barnard

Uma alternativa mais poderosa ao teste de Fisher em tabelas 2×2. Ele não assume margens fixas, o que pode tornar os resultados mais sensíveis, mas o método é menos implementado em software.

Teste de McNemar

Feito pra dados categóricos emparelhados ou combinados (por exemplo, pré vs. pós-tratamento nos mesmos indivíduos). Leva em conta a dependência entre as observações, mas não pode ser usado quando os pontos de dados são independentesent.

Considerações computacionais

O desempenho pode ser uma preocupação com o teste exato de Fisher, porque os cálculos ficam complicados quando a gente vai além das tabelas de contingência simples 2×2. Embora a extensão Freeman-Halton permita que o teste seja aplicado a tabelas 2×3 e 3×3, o custo computacional aumenta rapidamente à medida que o tamanho da tabela cresce. Por isso, algoritmos eficientes e otimizações são super importantes em áreas como genética e pesquisa clínica, onde testes precisos podem precisar ser feitos várias vezes em muitos conjuntos de dados pequenos, mas complexos.

Interpretação e relatórios estatísticos

Ao interpretar e relatar os resultados do teste exato de Fisher, é importante incluir o valor exato de p, fornecer a razão de chances juntamente com um intervalo de confiança de 95% e indicar claramente se foi realizado um teste unilateral ou bilateral. Os resultados também devem ser apoiados por um contexto prático para ajudar os leitores a entender o significado real das descobertas. Por exemplo, pode-se escrever: O teste exato de Fisher mostrou uma ligação significativa entre o tratamento e a recuperação (OR = 11,0, p = 0,02, bicaudal).

Extensões e Aplicações Avançadas

Extensões e aplicações avançadas do teste exato de Fisher ajudam a lidar com cenários de dados mais complexos e melhoram a precisão ao lidar com conjuntos de dados pequenos ou esparsos. A extensão Freeman–Halton permite que o teste seja aplicado a tabelas de contingência maiores, além do formato padrão 2×2, como tabelas 2×3 ou 3×3. O teste exato mid-P é uma alternativa menos conservadora ao teste de Fisher, melhorando o poder estatístico e mantendo a confiabilidade. Os testes exatos bayesianos usam o que já sabemos na análise, o que os torna super úteis quando os dados são limitados ou quando a opinião de especialistas pode ajudar na conclusão. Além disso, os métodos de correção de viés para odds ratios fornecem estimativas mais precisas do tamanho do efeito em estudos com amostras pequenas ou contagens zero, garantindo uma melhor interpretação da força e direção das associações.

Limitações e considerações metodológicas

O teste exato de Fisher pode ser conservador, o que pode reduzir o poder estatístico e dificultar a detecção de efeitos reais, especialmente em estudos pequenos. Quando os dados são muito escassos, pode ser complicado interpretar os resultados, porque os intervalos de confiança aumentam e as estimativas ficam instáveis. Além disso, fazer o teste várias vezes em muitas variáveis aumenta o risco de descobertas falsas, então é importante controlar com cuidado os testes múltiplos.

Visualizando tabelas de contingência

Boas opções de visualização para apresentar os resultados da tabela de contingência incluem gráficos de barras empilhadas, gráficos de barras lado a lado e gráficos mosaicos. Esses recursos visuais ajudam a mostrar de forma clara a relação entre variáveis categóricas e facilitam a interpretação de padrões ou diferenças entre grupos.

Aqui está um exemplo em Python:

import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd

df = pd.DataFrame({
    "Outcome": ["Recovered", "Not Recovered"] * 2,
    "Count": [8, 2, 4, 11],
    "Group": ["Treatment"] * 2 + ["Control"] * 2
})

sns.barplot(data=df, x="Outcome", y="Count", hue="Group")
plt.title("Treatment Outcomes")
plt.show()

Conclusão

O teste exato de Fisher continua sendo o padrão ouro para analisar pequenos conjuntos de dados categóricos. Nascido de uma xícara de chá em um jardim, ele se transformou numa ferramenta importante e muito usada na medicina, genética, pesquisa com seres humanos e experimentação empresarial.

Inscreva-se no nosso programa de Fundamentos de Estatística em Python para continuar aprendendo. Além de testes de hipóteses, ele vai te ajudar a praticar a construção de modelos estatísticos com regressão linear e logística.