Tutoriel sur la régression logistique en R

La régression logistique est un modèle simple mais puissant pour prédire des résultats binaires. Il s'agit de savoir si quelque chose va se produire ou non. Il s'agit d'un type de modèle de classification pour l'apprentissage automatique supervisé.

La régression logistique est utilisée dans presque tous les secteurs - marketing, santé, sciences sociales, etc. - et constitue un élément essentiel de la boîte à outils de tout scientifique des données.

Pour tirer le meilleur parti de ce tutoriel, vous devez avoir une connaissance de base de R. Il est également utile de connaître un type de modèle apparenté, la régression linéaire. Lisez le tutoriel sur la régression linéaire dans R pour en savoir plus à ce sujet.

Aperçu de la régression logistique

Supposons que vous souhaitiez prédire si la journée sera ensoleillée ou non. Il y a deux résultats possibles : "ensoleillé" ou "pas ensoleillé". La variable de résultat est également appelée "variable cible" ou "variable dépendante".

De nombreuses variables peuvent influencer le résultat, comme la température de la veille, la pression atmosphérique, etc. Les variables influentes sont appelées caractéristiques, variables indépendantes ou prédicteurs - tous ces termes signifient la même chose. 

D'autres exemples permettent de savoir si un client achètera votre produit ou non, si un courriel est un spam ou non, si une transaction est frauduleuse ou non, et si un médicament guérira un patient ou non.  

Comment fonctionne la régression logistique ?

La régression logistique trouve la meilleure adéquation possible entre les variables prédictives et les variables cibles afin de prédire la probabilité que la variable cible appartienne à une classe/catégorie étiquetée. 

La régression linéaire tente de trouver la meilleure ligne droite qui prédit le résultat à partir des caractéristiques. Il forme une équation du type

y_predictions = intercept + slope * features

et utilise l'optimisation pour essayer de trouver les meilleures valeurs possibles de l'ordonnée à l'origine et de la pente.

La régression logistique fonctionne de manière similaire, sauf qu'elle effectue une régression sur les probabilités que le résultat soit une catégorie. Il utilise une fonction sigmoïde (la fonction de distribution cumulative de la distribution logistique) pour transformer le côté droit de cette équation.

y_predictions = logistic_cdf(intercept + slope * features)

Là encore, le modèle utilise l'optimisation pour essayer de trouver les meilleures valeurs possibles de l'ordonnée à l'origine et de la pente.

L'algorithme de régression logistique étant très similaire à l'équation de régression linéaire, il fait partie d'une famille de modèles appelés "modèles linéaires généralisés". C'est pourquoi la régression logistique porte le nom de "régression", même s'il s'agit d'un modèle de classification.

La fonction sigmoïde ressemble à une courbe en forme de S dans l'image ci-dessous. Il prend les valeurs d'entrée numérotées réelles et les convertit entre 0 et 1 (en les réduisant des deux côtés, c'est-à-dire en ramenant les valeurs négatives à 0 et les valeurs positives très élevées à 1). En outre, le seuil de coupure est le facteur de décision superposé qui répartit les résultats en catégories ou classes lorsqu'il est appliqué en plus de ces probabilités.

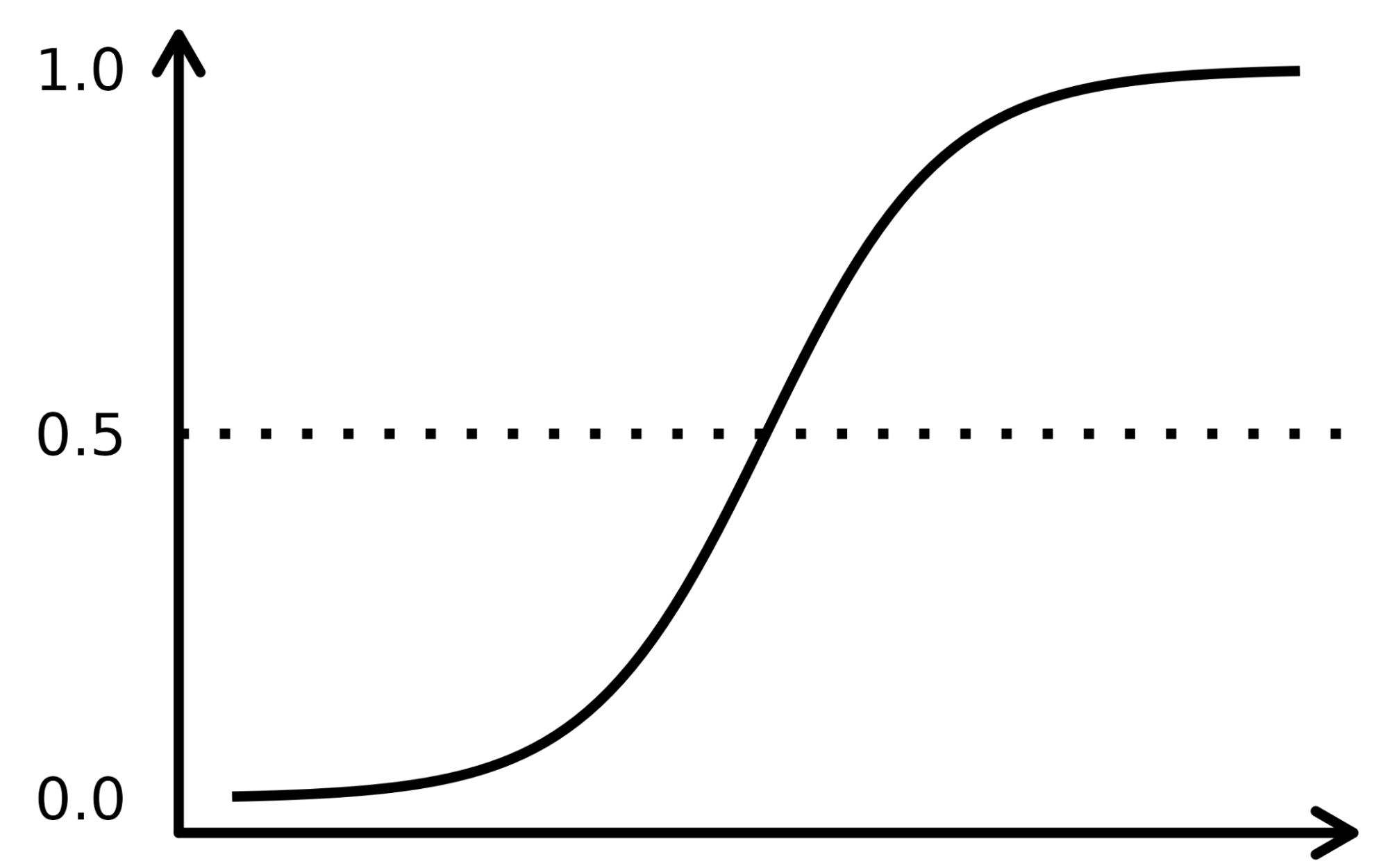
Les concepts complexes sont mieux compris lorsqu'ils sont expliqués à l'aide d'exemples. Prenons donc une analogie pour expliquer le fonctionnement de l'algorithme LR. Supposons que le modèle LR soit chargé d'identifier une transaction frauduleuse en examinant plusieurs indicateurs de fraude, tels que la localisation de l'utilisateur, le montant de l'achat, l'adresse IP, etc. L'objectif est de déterminer la probabilité qu'une transaction donnée soit légitime ou frauduleuse, ce qui constitue la variable cible.

Le modèle attribue des poids aux variables prédictives en fonction de leur impact sur la variable cible et les combine pour calculer le score normalisé ou la probabilité de fraude. 

L'ensemble de données

Nous utiliserons un ensemble de données relatives à une campagne de marketing direct menée par une institution bancaire portugaise au moyen d'appels téléphoniques. La campagne vise à vendre des souscriptions d'un dépôt bancaire à terme représenté par la variable y (souscription ou non). L'objectif du modèle de régression logistique est de prédire si un client achètera ou non un abonnement en fonction des variables prédictives, c'est-à-dire des attributs du client, tels que les informations démographiques.

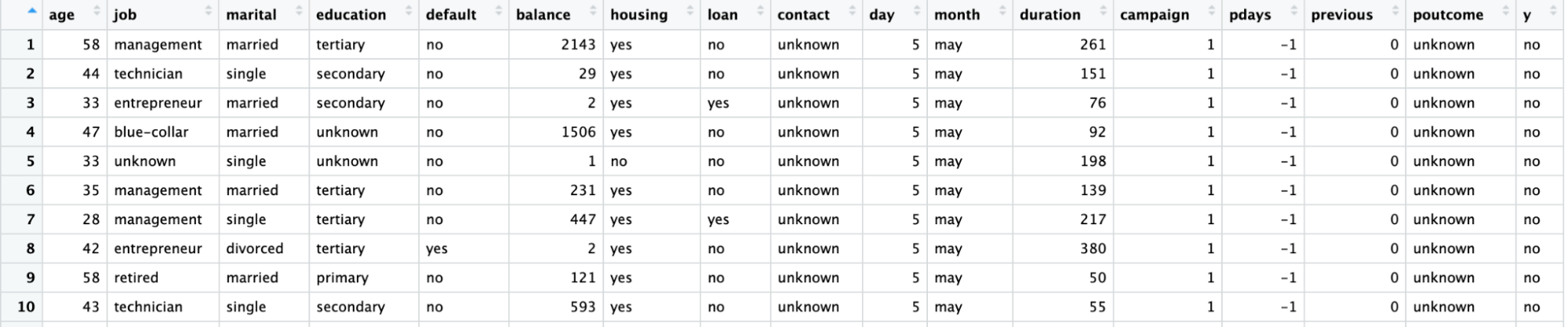
Le dictionnaire de données pour cet ensemble de données et de nombreux autres ensembles de données utiles peut être consulté sur le site web du DataCamp.

Processus de régression logistique

Le flux de travail complet de l'apprentissage automatique est présenté dans l'infographie Guide du débutant sur le flux de travail de l'apprentissage automatique. Nous nous concentrerons ici sur les étapes de préparation des données et de modélisation. En particulier, nous couvrirons les points suivants

• Diviser les données en ensembles de formation et de test
• Ajustement (entraînement) du modèle
• Faire des prévisions
• Évaluation de la performance du modèle
• Réglage des hyperparamètres

Paquets de régression logistique

En R, il existe deux flux de travail populaires pour modéliser la régression logistique : base-R et tidymodels.

Le modèle de flux de travail base-R est plus simple et comprend des fonctions telles que glm() et summary() pour ajuster le modèle et générer un résumé du modèle.

Le flux de travail tidymodels facilite la gestion de plusieurs modèles et offre une interface cohérente pour travailler avec différents types de modèles.

Ce tutoriel utilise le flux de travail tidymodels.

Visualiser les données

Importez le paquet tidymodels en appelant la fonction library(). 

L'ensemble des données se trouve dans un fichier CSV avec un formatage européen (virgules pour les décimales et points-virgules pour les séparateurs). Nous le lirons avec read_csv2() du paquet readr. 

Convertissez la variable cible, y, en une variable factorielle pour la modélisation. 

À l'aide de la fonction ggplot(), tracez le nombre de chaque profession en fonction de y.

library(readr)
library(tidymodels)

# Read the dataset and convert the target variable to a factor
bank_df <- read_csv2("bank-full.csv")
bank_df$y = as.factor(bank_df$y)

# Plot job occupation against the target variable
ggplot(bank_df, aes(job, fill = y)) +
    geom_bar() +
    coord_flip()

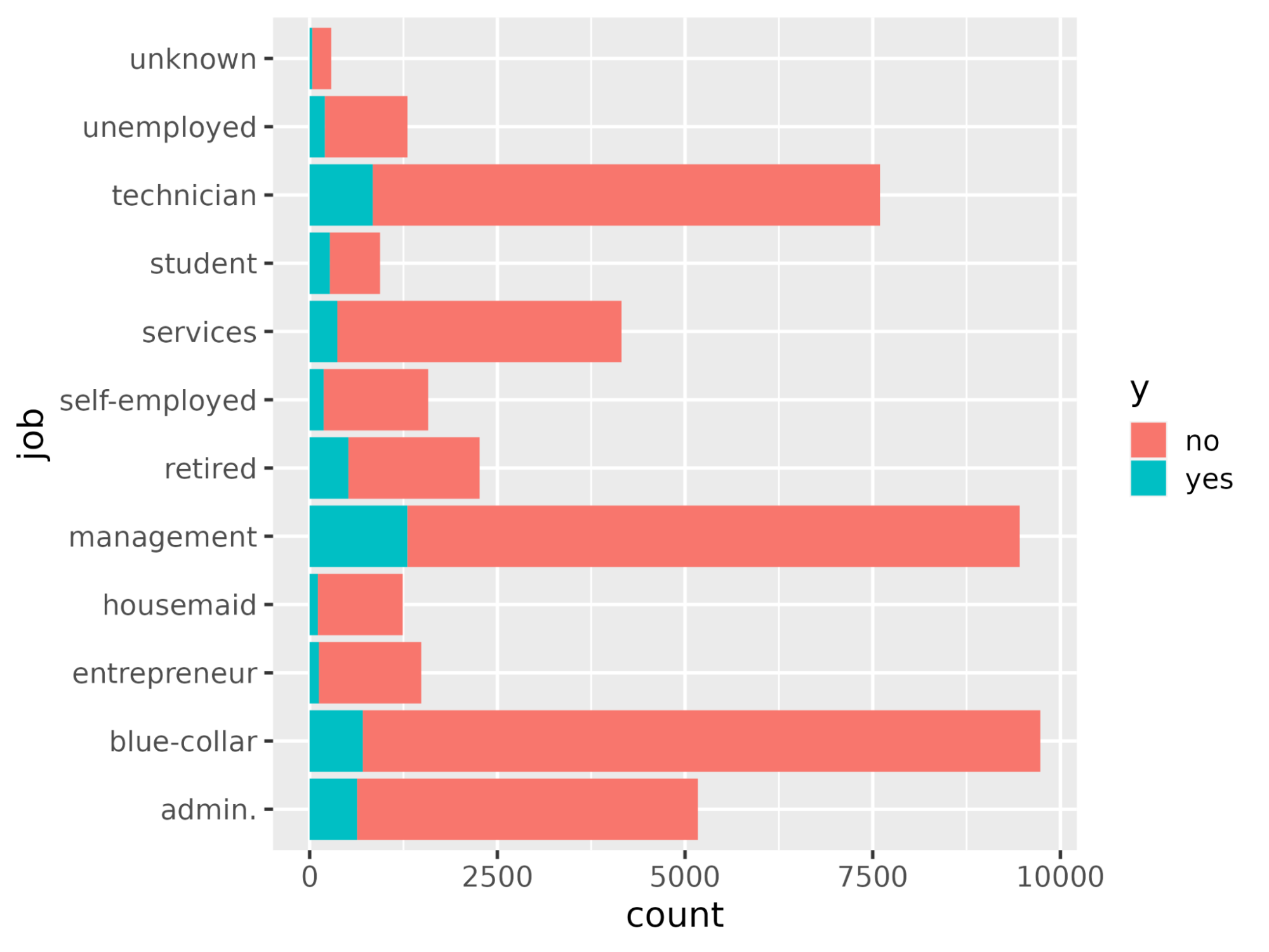
Diviser les données

Divisons l'ensemble de données en un ensemble de formation pour l'ajustement du modèle et un ensemble de test pour l'évaluation du modèle afin de s'assurer que le modèle ainsi formé fonctionne sur un ensemble de données inédit.

La division des données en ensembles de formation et de test peut être effectuée à l'aide de la fonction initial_split() et de l'attribut prop définissant la proportion de données de formation.

# Split data into train and test
set.seed(421)
split <- initial_split(bank_df, prop = 0.8, strata = y)
train <- split %>% 
         training()
test <- split %>% 
        testing()

Ajustement et évaluation du modèle

Pour créer le modèle, déclarez un modèle logistic_reg(). Cela nécessite des arguments de mélange et de pénalité qui contrôlent le degré de régularisation. Une valeur de mélange de 1 indique un modèle lasso et 0 indique une régression ridge. Les valeurs intermédiaires sont également autorisées. L'argument de la pénalité indique la force de la régularisation.

Notez que vous devez transmettre des nombres à virgule flottante "double" au mélange et à la pénalité

Définissez le "moteur" (le logiciel dorsal utilisé pour effectuer les calculs) à l'aide de la fonction set_engine(). Plusieurs choix s'offrent à vous : Le moteur par défaut est "glm", qui effectue une régression logistique classique. Cette méthode est souvent privilégiée par les statisticiens car elle permet d'obtenir des valeurs p pour chaque coefficient, ce qui facilite la compréhension de l'importance de chaque coefficient.

Nous utiliserons ici le moteur "glmnet". Cette méthode est privilégiée par les spécialistes de l'apprentissage automatique car elle permet une régularisation qui peut améliorer les prédictions, en particulier si vous disposez d'un grand nombre de caractéristiques. (Dans Python, le paquet scikit-learn inclut par défaut une certaine régularisation dans la régression logistique).

Appelez la méthode fit() pour entraîner le modèle sur les données d'entraînement créées à l'étape précédente. Cette fonction prend une formule comme premier argument. Dans la partie gauche de la formule, vous utilisez la variable cible (dans ce cas, y). Dans la partie droite, vous pouvez inclure toutes les caractéristiques que vous souhaitez. Un point signifie "utiliser toutes les variables qui n'ont pas été écrites dans la partie gauche de la formule". Pour plus d'informations sur l'écriture de formules, lisez le didacticiel sur les formules R.

# Train a logistic regression model
model <- logistic_reg(mixture = double(1), penalty = double(1)) %>%
  set_engine("glmnet") %>%
  set_mode("classification") %>%
  fit(y ~ ., data = train)

# Model summary
tidy(model)

La sortie est présentée ci-dessous, la colonne "estimation" représentant les coefficients du prédicteur.

# A tibble: 43 × 3
   term              estimate penalty
   <chr>                <dbl>   <dbl>
 1 (Intercept)      -2.59           0
 2 age              -0.000477       0
 3 jobblue-collar   -0.183          0
 4 jobentrepreneur  -0.206          0
 5 jobhousemaid     -0.270          0
 6 jobmanagement    -0.0190         0
 7 jobretired        0.360          0
 8 jobself-employed -0.101          0
 9 jobservices      -0.105          0
10 jobstudent        0.415          0
# ... with 33 more rows
# ℹ Use `print(n = ...)` to see more rows

Faire des prévisions

Faites des prédictions sur les données de test à l'aide de la fonction predict(). Vous avez le choix du type de prévisions.

• type = "class" renvoie la valeur cible la plus probable pour chaque observation. Dans ce cas, le modèle renvoie un "oui" ou un "non" selon qu'il estime que le client est susceptible de souscrire à un dépôt à terme ou non.
• type = "prob" renvoie la probabilité de chaque valeur cible pour chaque observation. Ici, il renverra la probabilité d'un "oui" et la probabilité d'un "non" (qui s'additionnent à un pour chaque observation).

# Class Predictions
pred_class <- predict(model,
                      new_data = test,
                      type = "class")

# Class Probabilities
pred_proba <- predict(model,
                      new_data = test,
                      type = "prob")

Évaluez le modèle à l'aide de la fonction accuracy() avec l'argument de vérité y et estimez que la valeur de l'argument correspond aux prédictions de l'étape précédente.

results <- test %>%
           select(y) %>%
           bind_cols(pred_class, pred_proba)

accuracy(results, truth = y, estimate = .pred_class)

Réglage des hyperparamètres

Plutôt que de transmettre des valeurs spécifiques aux arguments de mélange et de pénalité (les "hyperparamètres"), vous pouvez optimiser le pouvoir prédictif du modèle en le réglant. 

L'idée est d'exécuter le modèle un grand nombre de fois avec différentes valeurs des hyperparamètres et de voir lequel donne les meilleures prédictions.

• Dans la fonction logistic_reg(), définissez les arguments de mélange et de pénalité pour un appel à tune().
• Utilisez la fonction grid_regular() pour définir une grille de valeurs possibles pour le mélange et la pénalité.
• La fonction workflow() crée un objet pour stocker les détails du modèle, ce qui est nécessaire lorsque vous l'exécutez plusieurs fois. 
• Choisissez le meilleur modèle à l'aide de la fonction select_best(). Vous pouvez choisir parmi une série de mesures qui définissent la "meilleure". Nous utiliserons ici la métrique "receiver operating characteristic area under the curve" (ROC AUC).

# Define the logistic regression model with penalty and mixture hyperparameters
log_reg <- logistic_reg(mixture = tune(), penalty = tune(), engine = "glmnet")

# Define the grid search for the hyperparameters
grid <- grid_regular(mixture(), penalty(), levels = c(mixture = 4, penalty = 3))

# Define the workflow for the model
log_reg_wf <- workflow() %>%
  add_model(log_reg) %>%
  add_formula(y ~ .)

# Define the resampling method for the grid search
folds <- vfold_cv(train, v = 5)

# Tune the hyperparameters using the grid search
log_reg_tuned <- tune_grid(
  log_reg_wf,
  resamples = folds,
  grid = grid,
  control = control_grid(save_pred = TRUE)
)

select_best(log_reg_tuned, metric = "roc_auc")

# A tibble: 1 × 3
       penalty mixture .config              
         <dbl>   <dbl> <chr>                
1 0.0000000001       0 Preprocessor1_Model01

Plus de mesures d'évaluation

Utiliser les meilleurs hyperparamètres :

1. Entraînons un modèle de régression logistique
2. Utilisez-le pour générer des prédictions sur l'ensemble de test
3. Créez une matrice de confusion en utilisant les valeurs réelles et les estimations.

# Fit the model using the optimal hyperparameters
log_reg_final <- logistic_reg(penalty = 0.0000000001, mixture = 0) %>%
                 set_engine("glmnet") %>%
                 set_mode("classification") %>%
                 fit(y~., data = train)

# Evaluate the model performance on the testing set
pred_class <- predict(log_reg_final,
                      new_data = test,
                      type = "class")
results <- test %>%
  select(y) %>%
  bind_cols(pred_class, pred_proba)

# Create confusion matrix
conf_mat(results, truth = y,
         estimate = .pred_class)

Truth
Prediction   no  yes
       no  7838  738
       yes  147  320

Vous pouvez calculer la précision (valeur prédictive positive, nombre de vrais positifs divisé par le nombre de positifs prédits) à l'aide de la fonction precision().

precision(results, truth = y,
          estimate = .pred_class)

# A tibble: 1 × 3
  .metric   .estimator .estimate
  <chr>     <chr>          <dbl>
1 precision binary         0.914

De même, vous pouvez calculer le rappel (sensibilité, nombre de vrais positifs divisé par le nombre de vrais positifs) à l'aide de la fonction recall().

recall(results, truth = y,
          estimate = .pred_class)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 recall  binary         0.982

Comprenons les variables qui influencent la décision d'achat d'un abonnement. Dans un scénario de régression logistique, les coefficients déterminent le degré de sensibilité de la variable cible aux prédicteurs individuels. Plus la valeur des coefficients est élevée, plus leur importance est grande. Trier les variables par ordre décroissant de la valeur absolue de leurs coefficients et n'afficher que les coefficients dont la valeur absolue est supérieure à 0,5.

coeff <- tidy(log_reg_final) %>% 
  arrange(desc(abs(estimate))) %>% 
  filter(abs(estimate) > 0.5)

# A tibble: 10 × 3
   term            estimate      penalty
   <chr>              <dbl>        <dbl>
 1 (Intercept)       -2.59  0.0000000001
 2 poutcomesuccess    2.08  0.0000000001
 3 monthmar           1.62  0.0000000001
 4 monthoct           1.08  0.0000000001
 5 monthsep           1.03  0.0000000001
 6 contactunknown    -1.01  0.0000000001
 7 monthdec           0.861 0.0000000001
 8 monthjan          -0.820 0.0000000001
 9 housingyes        -0.550 0.0000000001
10 monthnov          -0.517 0.0000000001

Tracez l'importance des caractéristiques à l'aide de la fonction ggplot().

ggplot(coeff, aes(x = term, y = estimate, fill = term)) + geom_col() + coord_flip()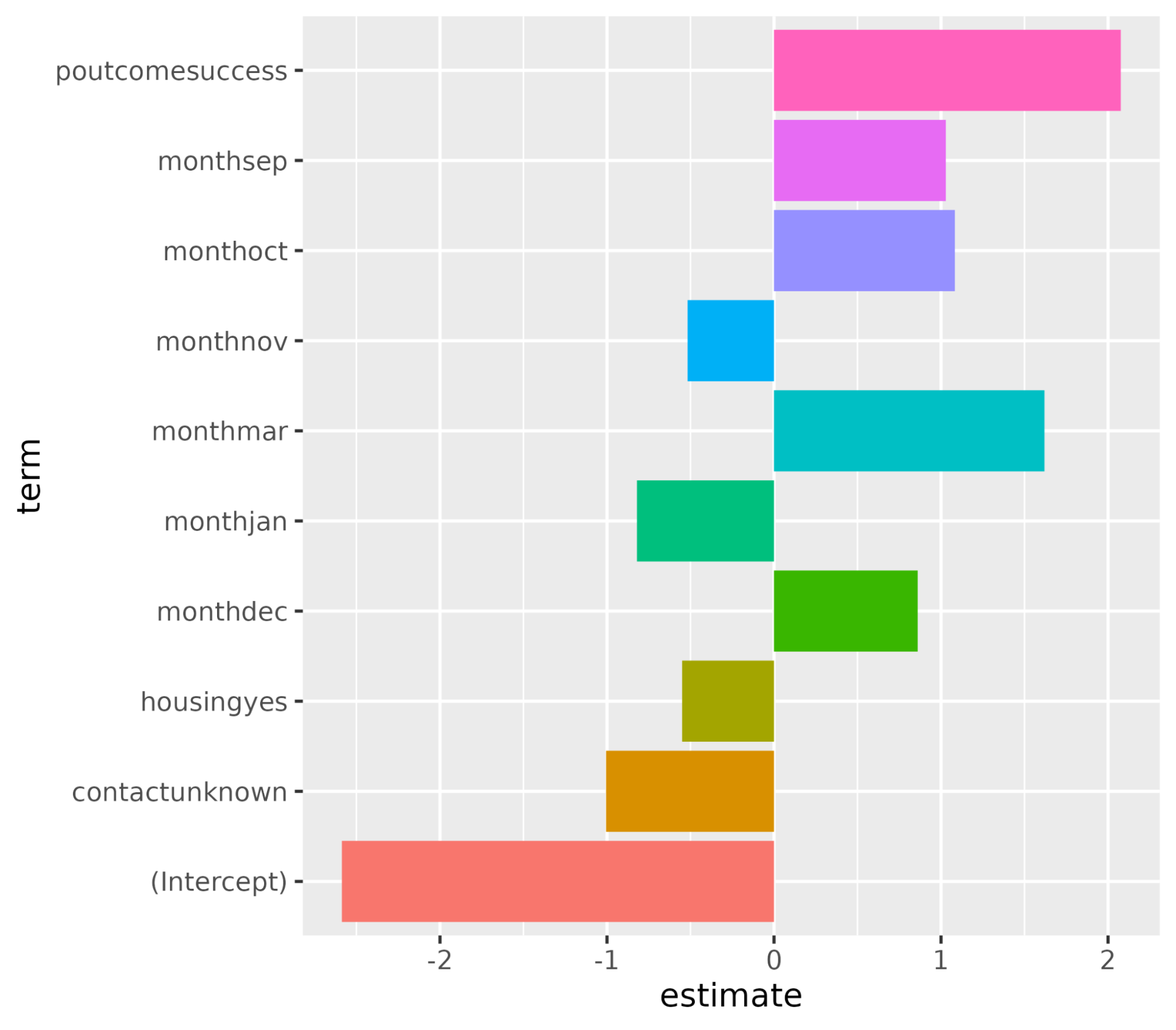

Passez au niveau supérieur

Ainsi, nous sommes arrivés à la fin de ce tutoriel qui a démontré comment entraîner et évaluer un modèle de régression logistique à l'aide du paquetage tidymodels. Il a également abordé la manière d'interpréter les résultats du modèle et de les représenter graphiquement, comme l'importance des caractéristiques. 

Si vous souhaitez en savoir plus sur la modélisation de modèles d'IA à l'aide de tidymodels, consultez le cours Modeling with tidymodels in R (Modélisation avec tidymodels en R). Pour la modélisation à l'aide de l'approche de base R, consultez les cours Introduction à la régression en R, Régression intermédiaire en R et Modèles linéaires généralisés en R.