Cours
La régression linéaire est l'une des techniques statistiques les plus importantes et les plus fondamentales. La maîtrise de cette technique est essentielle pour tout analyste et scientifique des données car, comme vous le verrez, elle constitue la base de nombreuses méthodes plus avancées.
Ce tutoriel vous guidera à travers le processus de régression linéaire dans R, qui est un langage de programmation important. À la fin de ce tutoriel, vous comprendrez comment mettre en œuvre et interpréter les modèles de régression linéaire, ce qui facilitera l'application de ces connaissances à vos tâches d'analyse de données.
Si vous n'êtes pas familier avec le langage de programmation R, je vous recommande nos tutoriels DataCamp pour commencer : Exploratory Data Analysis in R for Absolute Beginners et Mastering Data Structures in the R Programming Language.
Qu'est-ce que la régression linéaire ?
Une régression linéaire est un modèle statistique qui analyse la relation entre une variable de réponse (souvent appelée y) et une ou plusieurs variables et leurs interactions (souvent appelées x ou variables explicatives). Par exemple, lorsque vous calculez l'âge d'un enfant en fonction de sa taille, vous supposez que plus il est âgé, plus il est grand.
La régression linéaire est l'un des modèles statistiques les plus élémentaires. Ses résultats peuvent être interprétés par presque tout le monde et elle existe depuis le 19e siècle. C'est précisément ce qui rend la régression linéaire si populaire. C'est simple et cela a survécu pendant des centaines d'années. Même si elle n'est pas aussi sophistiquée que d'autres algorithmes comme les réseaux neuronaux artificiels ou les forêts aléatoires, selon une enquête réalisée par KD Nuggets, la régression a été l'algorithme le plus utilisé par les data scientists en 2016 et 2017. On prévoit même qu'il sera encore utilisé en 2118!
Dans ce tutoriel sur la régression linéaire, nous allons voir comment créer une régression linéaire dans R, en examinant les étapes à suivre avec un exemple que vous pouvez utiliser.
Pour exécuter facilement vous-même tous les exemples de code de ce tutoriel, vous pouvez créer gratuitement un classeur DataLab dans lequel R est préinstallé et qui contient tous les exemples de code. Pour plus de pratique sur la régression linéaire, consultez cet exercice pratique de DataCamp.
Comment créer une régression linéaire dans R
Tous les problèmes ne peuvent pas être résolus avec le même algorithme. On dit que la régression linéaire est bonne lorsqu'il existe une relation linéaire entre la réponse et le résultat. En d'autres termes, la régression linéaire suppose qu'il existe une relation linéaire entre la variable de réponse et les variables explicatives. Dans le cas de deux variables, cela signifie que vous pouvez tracer une ligne entre les deux variables. Si l'on reprend l'exemple précédent de l'âge de l'enfant, il est clair qu'il existe une relation entre l'âge des enfants et leur taille.
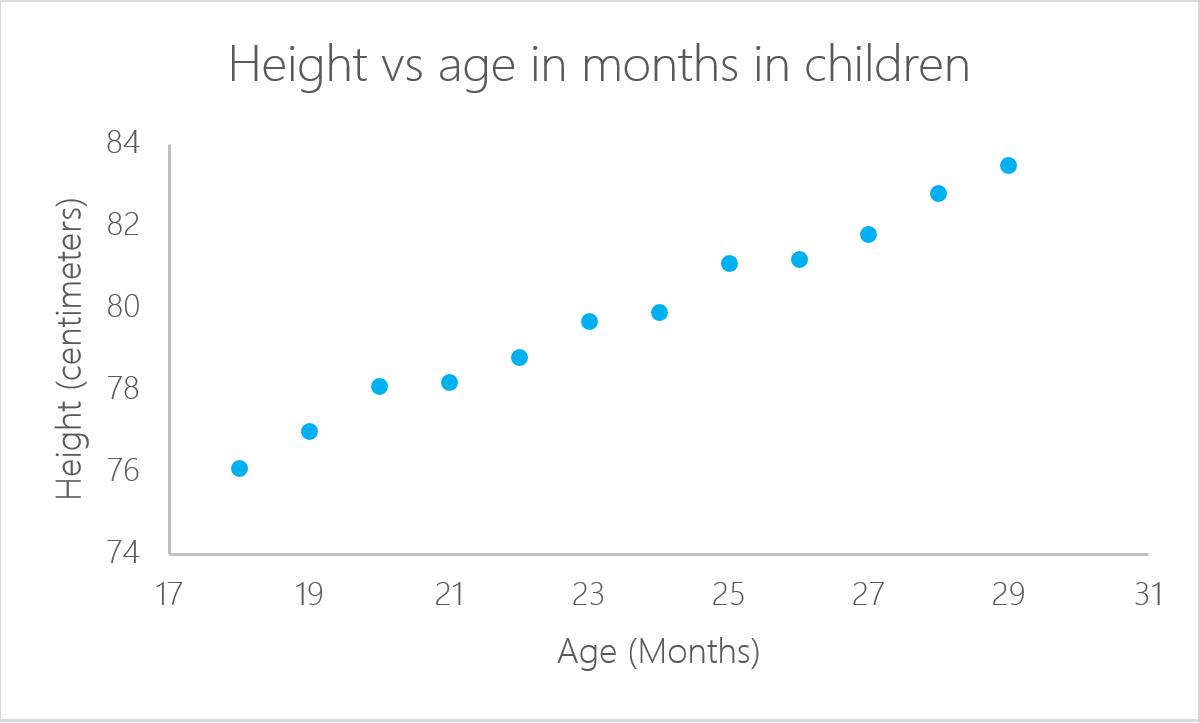
Dans cet exemple particulier, vous pouvez calculer la taille d'un enfant si vous connaissez son âge :
![]()
Dans ce cas, a et b sont appelés respectivement l'ordonnée à l'origine et la pente. Dans le même exemple, a, ou l'ordonnée à l'origine, est la valeur à partir de laquelle vous commencez à mesurer. Les nouveau-nés âgés de zéro mois ne mesurent pas zéro centimètre. C'est la fonction de l'intercept. La pente mesure la variation de la taille par rapport à l'âge en mois. En général, pour chaque mois d'âge de l'enfant, sa taille augmente avec b.
lm() dans R
Une régression linéaire peut être calculée dans R avec la commande lm(). Dans l'exemple suivant, nous utilisons cette commande pour calculer la taille estimée en fonction de l'âge de l'enfant.
Tout d'abord, importez la bibliothèque readxl pour lire les fichiers Microsoft Excel. Notre cours Introduction à l'importation de données dans R est une excellente ressource si vous n'êtes pas familiarisé avec l'importation de fichiers Excel ou CSV dans un environnement R tel que RStudio.
Vous pouvez télécharger les données à utiliser pour ce tutoriel avant de commencer. Téléchargez les données dans un objet appelé ageandheight et créez ensuite la régression linéaire dans la troisième ligne. La fonction lm() prend les variables au format :
lm([target] ~ [predictor], data = [data source])Dans le code suivant, nous utilisons la fonction lm() pour créer un objet modèle linéaire, que nous appelons lmHeight. Nous utilisons ensuite la fonction summary() sur lmHeight afin d'obtenir des informations détaillées sur les performances et les coefficients du modèle.
library(readxl)
ageandheight <- read_excel("ageandheight.xls", sheet = "Hoja2") #Upload the data
lmHeight = lm(height~age, data = ageandheight) #Create the linear regression
summary(lmHeight) #Review the resultsApprendre R pour l'apprentissage automatique
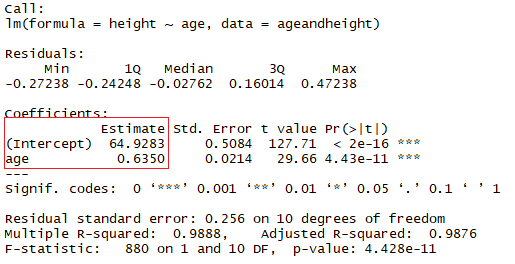
Que sont les coefficients ?
Dans le carré rouge, vous pouvez voir les valeurs de l'ordonnée à l'origine (valeur "a") et de la pente (valeur "b") pour l'âge. Ces valeurs "a" et "b" tracent une ligne entre tous les points des données. Ainsi, dans ce cas, si un enfant est âgé de 20,5 mois, que a vaut 64,92 et que b vaut 0,635, le modèle prédit (en moyenne) que sa taille en centimètres est d'environ 64,92 + (0,635 * 20,5) = 77,93 cm.
Lorsqu'une régression prend en compte deux prédicteurs ou plus pour créer la régression linéaire, on parle de régression linéaire multiple. Selon la même logique que celle utilisée dans l'exemple simple précédent, la taille de l'enfant sera mesurée par :
Taille = a + Âge × b1 + (Nombre de frères et sœurs} × b2
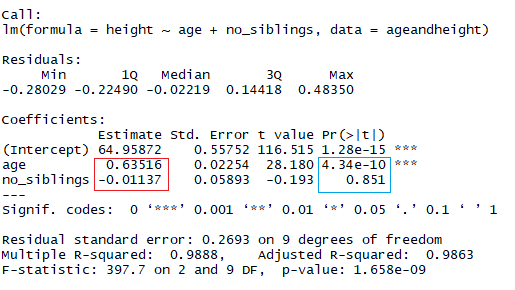
Vous étudiez maintenant la taille en fonction de l'âge en mois et du nombre de frères et sœurs de l'enfant. Dans l'image ci-dessus, le rectangle rouge indique les coefficients (b1 et b2). Vous pouvez interpréter ces coefficients de la manière suivante :
Lorsque l'on compare des enfants ayant le même nombre de frères et sœurs, la taille moyenne prédite augmente de 0,63 cm pour chaque mois que compte l'enfant. De même, lorsque l'on compare des enfants du même âge, la taille diminue (car le coefficient est négatif) de -0,01 cm pour chaque augmentation du nombre de frères et sœurs.
Dans R, pour ajouter un coefficient supplémentaire, ajoutez le symbole "+" pour chaque variable supplémentaire que vous souhaitez ajouter au modèle.
lmHeight2 = lm(height~age + no_siblings, data = ageandheight) #Create a linear regression with two variables
summary(lmHeight2) #Review the resultsComme vous l'avez peut-être déjà remarqué, le nombre de frères et sœurs est un moyen stupide de prédire la taille d'un enfant. Un autre aspect auquel vous devez prêter attention dans vos modèles linéaires est la valeur p des coefficients. Dans l'exemple précédent, le rectangle bleu indique les valeurs p pour les coefficients âge et nombre de frères et sœurs. En termes simples, une valeur p indique si vous pouvez rejeter ou accepter une hypothèse. L'hypothèse, dans ce cas, est que le prédicteur n'est pas significatif pour votre modèle.
- La valeur p pour l'âge est de 4,34*e-10 ou 0,000000000434. Une valeur très faible signifie que l'âge est probablement un excellent ajout à votre modèle.
- La valeur p pour le nombre de frères et sœurs est de 0,85. En d'autres termes, il y a 85 % de chances que ce prédicteur ne soit pas significatif pour la régression.
Une manière standard de tester si les prédicteurs ne sont pas significatifs est de regarder si les valeurs p sont inférieures à 0,05.
Qu'est-ce qu'un résidu ?
Un bon moyen de tester la qualité de l'ajustement du modèle est d'examiner les résidus ou les différences entre les valeurs réelles et les valeurs prédites. La ligne droite dans l'image ci-dessus représente les valeurs prédites. La ligne verticale rouge entre la ligne droite et la valeur observée des données est le résidu.
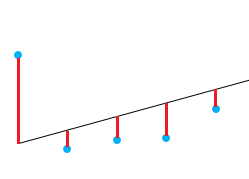
L'idée est ici que la somme des résidus soit approximativement nulle ou aussi faible que possible. Dans la réalité, la plupart des cas ne suivent pas une ligne parfaitement droite, et il faut donc s'attendre à des résidus. Dans le résumé R de la fonction lm(), vous pouvez voir des statistiques descriptives sur les résidus du modèle, en suivant le même exemple, le carré rouge montre que les résidus sont approximativement nuls.
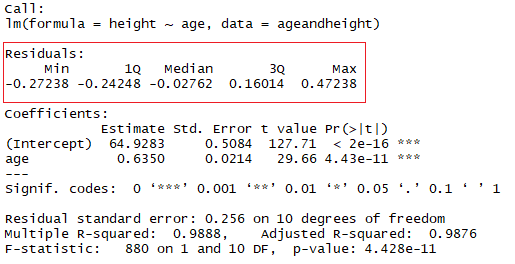
Comment tester l'adéquation de votre modèle linéaire ?
Le coefficient de détermination ou R² est une mesure très utilisée pour tester la qualité de votre modèle. Cette mesure est définie par la proportion de la variabilité totale expliquée par le modèle de régression.
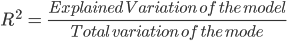
Cela peut sembler un peu compliqué, mais en général, pour les modèles qui s'adaptent bien aux données, le R² est proche de 1. Les modèles qui correspondent mal aux données ont un R² proche de 0. Dans les exemples ci-dessous, le premier a un R² de 0,02, ce qui signifie que le modèle n'explique que 2 % de la variabilité des données. Le second a un R² de 0,99, et le modèle peut expliquer 99% de la variabilité totale**.
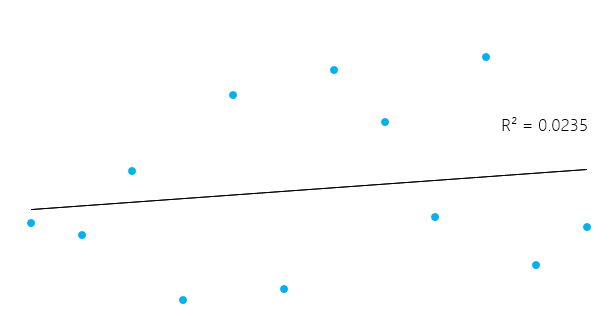
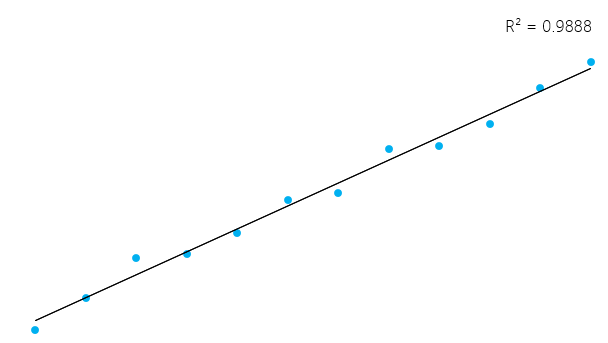
Cependant, il est essentiel de garder à l'esprit que parfois un R² élevé n'est pas nécessairement bon dans tous les cas (voir les graphiques résiduels ci-dessous) et qu'un R² faible n'est pas nécessairement mauvais dans tous les cas. Dans la vie réelle, les événements ne suivent pas toujours une ligne parfaitement droite. Par exemple, vous pouvez avoir dans vos données des enfants plus grands ou plus petits ayant le même âge. Dans certains domaines, un R² de 0,5 est considéré comme bon.
Avec le même exemple que ci-dessus, regardez le résumé du modèle linéaire pour voir son R².
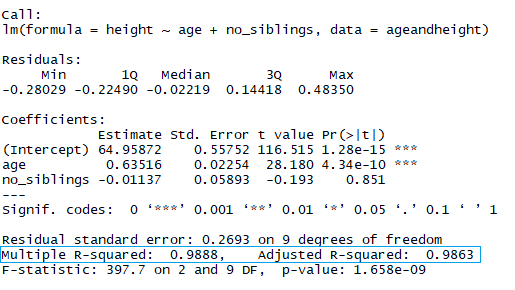
Dans le rectangle bleu, remarquez qu'il y a deux R² différents, l'un multiple et l'autre ajusté. Le multiple est le R² que vous avez vu précédemment. Le problème de ce R² est qu'il ne peut pas diminuer lorsque vous ajoutez des variables indépendantes à votre modèle. Il continuera d'augmenter à mesure que vous rendez le modèle plus complexe, même si ces variables n'ajoutent rien à vos prédictions (comme dans l'exemple du nombre de frères et sœurs). C'est pourquoi il est probablement préférable d'examiner le R² ajusté si vous ajoutez plus d'une variable au modèle, car il n'augmente que s'il réduit l'erreur globale des prédictions.
Examiner les résidus
Vous pouvez avoir un très bon R² dans votre modèle, mais ne tirons pas de conclusions hâtives. Prenons un exemple. Vous allez prédire la pression d'un matériau en laboratoire en fonction de sa température.
Traçons les données (dans un simple nuage de points) et ajoutons la ligne que vous avez construite avec votre modèle linéaire. Dans cet exemple, laissez R lire d'abord les données, toujours avec la commande read_excel, pour créer un cadre de données avec les données, puis créez une régression linéaire avec vos nouvelles données. La commande plot() prend un cadre de données et y trace les variables. Dans ce cas, il représente la pression en fonction de la température du matériau. Ajoutez ensuite la ligne obtenue par la régression linéaire à l'aide de la commande abline.
pressure <- read_excel("pressure.xlsx") #Upload the data
lmTemp = lm(Pressure~Temperature, data = pressure) #Create the linear regression
plot(pressure, pch = 16, col = "blue") #Plot the results
abline(lmTemp) #Add a regression line
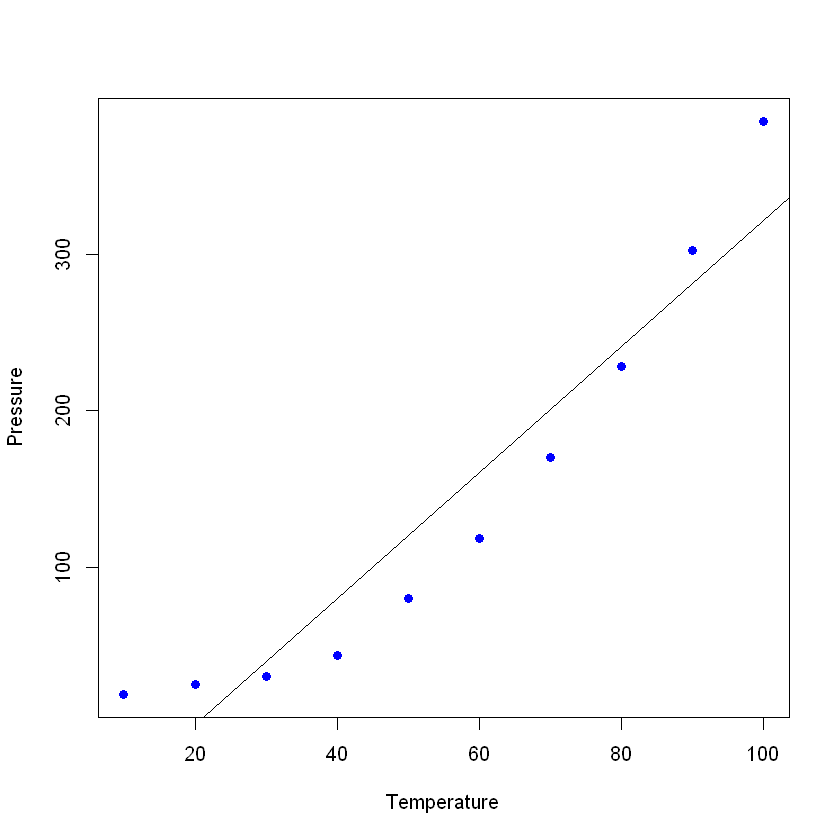
Si vous consultez le résumé de votre nouveau modèle, vous constaterez qu'il donne d'assez bons résultats (regardez le R² et le R² ajusté).
summary(lmTemp)
Call:
lm(formula = Pressure ~ Temperature, data = pressure)
Residuals:
Min 1Q Median 3Q Max
-41.85 -34.72 -10.90 24.69 63.51
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -81.5000 29.1395 -2.797 0.0233 *
Temperature 4.0309 0.4696 8.583 2.62e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 42.66 on 8 degrees of freedom
Multiple R-squared: 0.902, Adjusted R-squared: 0.8898
F-statistic: 73.67 on 1 and 8 DF, p-value: 2.622e-05Idéalement, lorsque vous tracez les résidus, ils doivent avoir un aspect aléatoire. Dans le cas contraire, cela signifie qu'il existe peut-être un modèle caché que le modèle linéaire ne prend pas en compte. Pour tracer les résidus, utilisez la commande plot(lmTemp$residuals).
plot(lmTemp$residuals, pch = 16, col = "red")
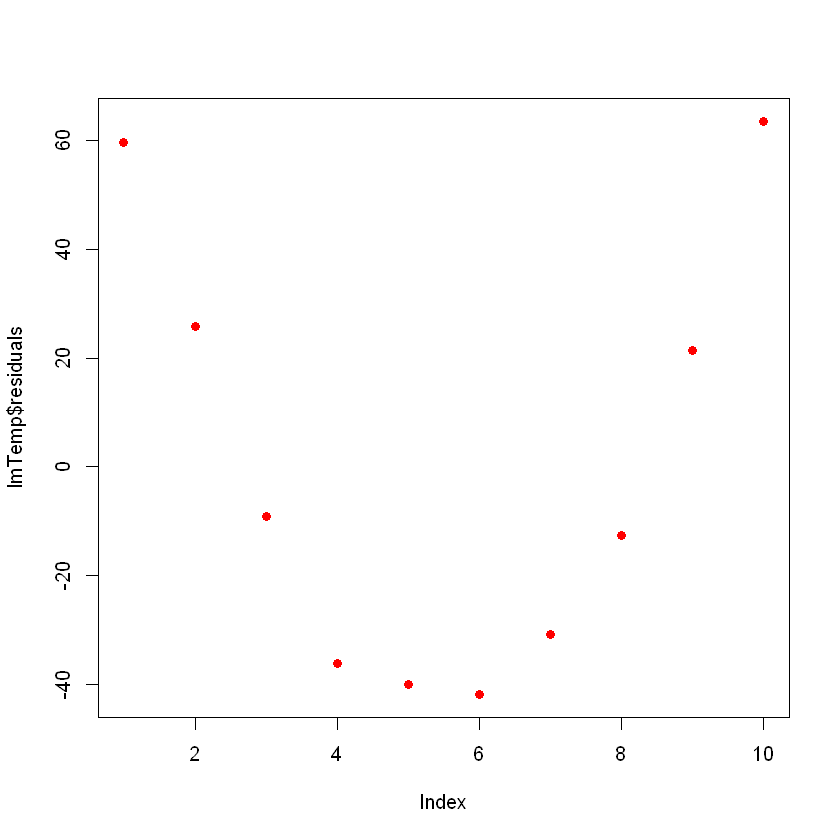
Cela peut poser un problème. Si vous disposez de plus de données, votre modèle linéaire simple ne sera pas en mesure de bien se généraliser. Dans l'image précédente, remarquez qu'il y a un schéma (comme une courbe sur les résidus). Ce n'est pas du tout un hasard.
Ce que vous pouvez faire, c'est transformer la variable. De nombreuses transformations peuvent être effectuées sur vos données, comme l'ajout d'un terme quadratique (x 2), d'un terme cubique (x3), ou d'un terme plus complexe tel que ln(X), ln(X+1), sqrt(X), 1/x, Exp(X). Le choix de la transformation correcte est le fruit d'une certaine connaissance des fonctions algébriques, de la pratique, d'essais et d'erreurs.
Essayons avec un terme quadratique. Pour cela, ajoutez le terme "I" (I majuscule) devant votre transformation, par exemple, il s'agira de la formule de régression linéaire normale :
lmTemp2 = lm(Pressure~Temperature + I(Temperature^2), data = pressure) #Create a linear regression with a quadratic coefficient
summary(lmTemp2) #Review the results
Call:
lm(formula = Pressure ~ Temperature + I(Temperature^2), data = pressure)
Residuals:
Min 1Q Median 3Q Max
-4.6045 -1.6330 0.5545 1.1795 4.8273
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 33.750000 3.615591 9.335 3.36e-05 ***
Temperature -1.731591 0.151002 -11.467 8.62e-06 ***
I(Temperature^2) 0.052386 0.001338 39.158 1.84e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.074 on 7 degrees of freedom
Multiple R-squared: 0.9996, Adjusted R-squared: 0.9994
F-statistic: 7859 on 2 and 7 DF, p-value: 1.861e-12Remarquez que le modèle s'est considérablement amélioré. Si vous tracez les résidus du nouveau modèle, ils ressembleront à ceci :
plot(lmTemp2$residuals, pch = 16, col = "red")
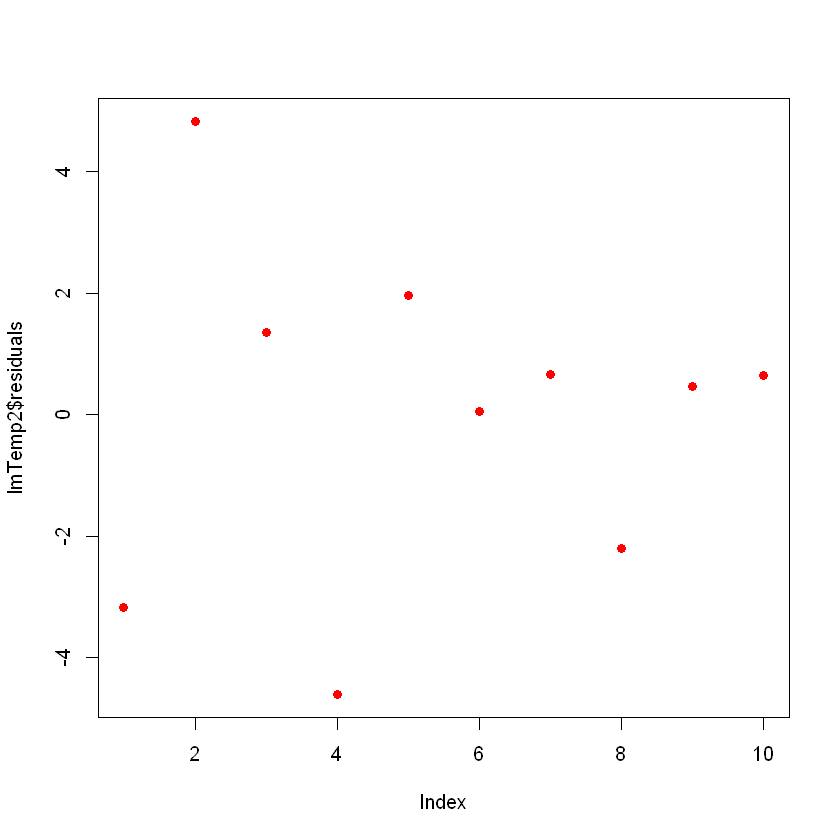
Aujourd'hui, vous n'observez aucun schéma clair dans vos résidus, ce qui est une bonne chose !
Détecter les points d'influence
Dans vos données, vous pouvez avoir des points d'influence qui peuvent fausser votre modèle, parfois inutilement. Pensez à une erreur dans la saisie des données, et au lieu d'écrire "2.3", la valeur était "23". Le type de point influent le plus courant est celui des valeurs aberrantes, c'est-à-dire des points de données où la réponse observée ne semble pas suivre le modèle établi par le reste des données.
Vous pouvez détecter les points influents en regardant l'objet contenant le modèle linéaire, à l'aide de la fonction cooks.distance(), puis en traçant ces distances. Modifiez volontairement une valeur pour voir ce qu'elle donne sur le graphique de la distance de Cooks. Pour modifier une valeur spécifique, vous pouvez la pointer directement avec ageandheight[row number, column number] = [new value]. Dans ce cas, la hauteur est modifiée pour atteindre 7,7 dans le deuxième exemple :
ageandheight[2, 2] = 7.7
head(ageandheight)
| âge | hauteur | no_siblings |
|---|---|---|
| 18 | 76.1 | 0 |
| 19 | 7.7 | 2 |
| 20 | 78.1 | 0 |
| 21 | 78.2 | 3 |
| 22 | 78.8 | 4 |
| 23 | 79.7 | 1 |
Vous créez à nouveau le modèle et voyez comment le résumé donne un mauvais ajustement, puis vous tracez les distances de Cooks. Pour cela, après avoir créé la régression linéaire, utilisez la commande cooks.distance([linear model], puis, si vous le souhaitez, vous pouvez tracer ces distances avec la commande plot().
lmHeight3 = lm(height~age, data = ageandheight)#Create the linear regression
summary(lmHeight3)#Review the results
plot(cooks.distance(lmHeight3), pch = 16, col = "blue") #Plot the Cooks Distances.
Call:
lm(formula = height ~ age, data = ageandheight)
Residuals:
Min 1Q Median 3Q Max
-53.704 -2.584 3.609 9.503 17.512
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.905 38.319 0.206 0.841
age 2.816 1.613 1.745 0.112
Residual standard error: 19.29 on 10 degrees of freedom
Multiple R-squared: 0.2335, Adjusted R-squared: 0.1568
F-statistic: 3.046 on 1 and 10 DF, p-value: 0.1115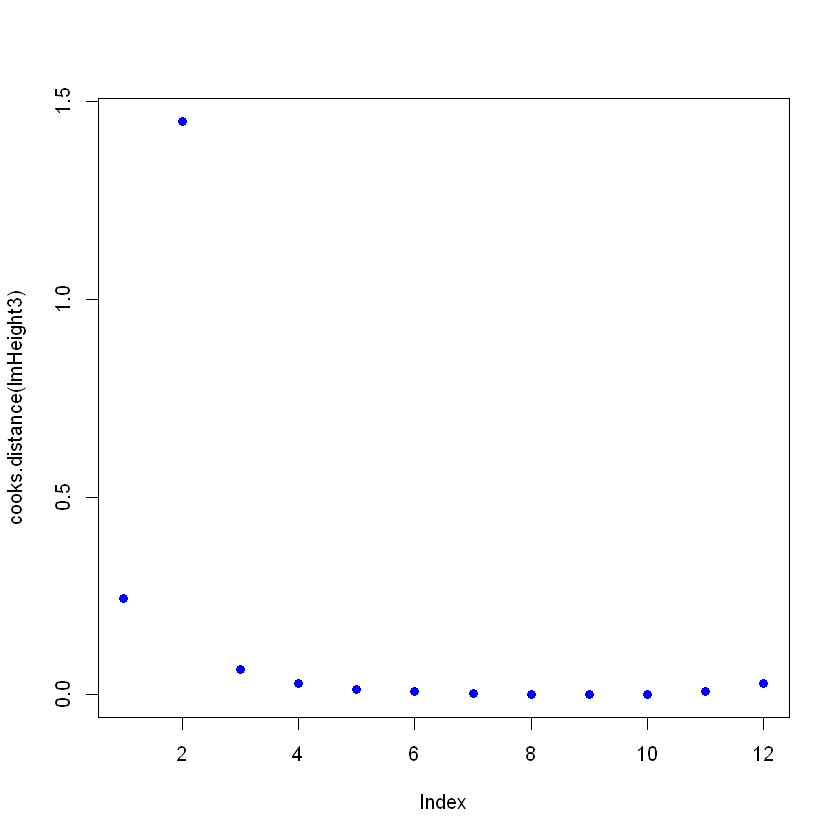
Remarquez qu' il y a un point qui ne suit pas le modèle et qui pourrait l'affecter. Ici, vous pouvez prendre des décisions sur ce point, en général, il y a trois raisons pour lesquelles un point est si influent :
- Quelqu'un a fait une erreur d'enregistrement
- Quelqu'un a commis une erreur fondamentale en recueillant l'observation
- Le point de données est parfaitement valide, auquel cas le modèle ne peut pas expliquer le comportement.
Si le cas est 1 ou 2, vous pouvez supprimer le point (ou le corriger). Si c'est 3, cela ne vaut pas la peine de supprimer un point valable ; vous pouvez peut-être essayer un modèle non linéaire plutôt qu'un modèle linéaire comme la régression linéaire.
Attention, un point influent peut être un point valide, veillez à vérifier les données et leur source avant de les supprimer. Il est courant de voir cette citation dans les livres de statistiques : "Parfois, nous rejetons des données parfaitement bonnes alors que nous devrions rejeter des modèles douteux.
Conclusion
Vous êtes arrivé au bout ! La régression linéaire est un sujet important, et elle est là pour rester. Nous vous présentons ici quelques astuces qui peuvent vous aider à régler et à tirer le meilleur parti d'un algorithme aussi puissant que simple. Vous avez également appris à comprendre ce qui se cache derrière ce modèle statistique simple et à le modifier en fonction de vos besoins. Vous pouvez également explorer d'autres options en tapant ?lm dans la console R et en examinant les différents paramètres qui ne sont pas abordés ici. Consultez notre tutoriel sur la régularisation : Ridge, Lasso et Elastic Net. Si vous souhaitez vous plonger dans les modèles statistiques, consultez le cours sur la modélisation statistique en R.
Améliorez les compétences de votre équipe en matière de données grâce à l'apprentissage continu
La régression linéaire étant à la base de nombreuses techniques analytiques avancées, il est essentiel pour votre réussite à long terme que votre équipe ait une bonne maîtrise de cette technique et d'autres compétences essentielles.
DataCamp for Business offre une solution sur mesure aux organisations qui cherchent à renforcer les compétences de leurs équipes en matière de science des données et d'analyse. Grâce à des parcours d'apprentissage personnalisés et à des cours pratiques couvrant un large éventail de méthodes statistiques, y compris la régression et la modélisation prédictive, votre équipe peut relever en toute confiance des défis complexes en matière de données.
Demandez une démonstration dès aujourd'hui et investissez dans l'avenir de votre organisation en permettant à votre équipe de rester au fait des derniers outils et techniques en matière d'analyse de données.
Obtenez une certification dans le rôle de Data Scientist de vos rêves
Nos programmes de certification vous aident à vous démarquer et à prouver aux employeurs potentiels que vos compétences sont adaptées à l'emploi.
Questions fréquemment posées
Qu'est-ce que R^2 dans la régression linéaire ?
R^2, ou coefficient de détermination, mesure la proportion de la variance de la variable dépendante qui est prévisible à partir de la ou des variables indépendantes. Il est compris entre 0 et 1, les valeurs les plus élevées indiquant une meilleure adéquation.
Qu'est-ce que la formule du R au carré ?
Le R au carré est calculé comme la proportion de la variabilité totale de la variable dépendante qui est expliquée par le modèle de régression. Il compare la somme des différences au carré entre les valeurs observées et prédites à la somme totale des différences au carré par rapport à la moyenne des valeurs observées.
Quelle est la signification de R dans la régression linéaire ?
Dans la régression linéaire, R représente le coefficient de corrélation entre les valeurs observées et prédites de la variable dépendante. Il indique la force et la direction de la relation linéaire.