Regresión logística en R Tutorial

La regresión logística es un modelo sencillo pero potente para predecir resultados binarios. Es decir, si algo sucederá o no. Es un tipo de modelo de clasificación para el aprendizaje automático supervisado.

La regresión logística se utiliza en casi todos los sectores (marketing, sanidad, ciencias sociales, etc.) y es una parte esencial de las herramientas de cualquier científico de datos.

Para sacar el máximo partido de este tutorial es necesario tener conocimientos básicos de R. También ayuda conocer un tipo de modelo relacionado, la regresión lineal. Lea el tutorial Regresión lineal en R para obtener más información al respecto.

Visión general de la regresión logística

Supongamos que quieres predecir si hoy va a ser un día soleado o no. Hay dos resultados posibles: "soleado" o "no soleado". La variable de resultado también se conoce como "variable objetivo" o "variable dependiente".

Hay muchas variables que pueden influir en el resultado, como "la temperatura del día anterior", "la presión atmosférica", etc. Las variables que influyen se conocen como características, variables independientes o predictores; todos estos términos significan lo mismo. 

Otros ejemplos son si un cliente comprará su producto o no, si un correo electrónico es spam o no, si una transacción es fraudulenta o no, y si un medicamento curará a un paciente o no.  

¿Cómo funciona la regresión logística?

La regresión logística encuentra el mejor ajuste posible entre las variables predictoras y objetivo para predecir la probabilidad de que la variable objetivo pertenezca a una clase/categoría etiquetada. 

La regresión lineal intenta encontrar la mejor línea recta que prediga el resultado a partir de las características. Forma una ecuación como

y_predictions = intercept + slope * features

y utiliza la optimización para intentar encontrar los mejores valores posibles de intercepto y pendiente.

La regresión logística funciona de forma similar, salvo que realiza la regresión sobre las probabilidades de que el resultado sea una categoría. Utiliza una función sigmoidea (la función de distribución acumulativa de la distribución logística) para transformar el lado derecho de esa ecuación.

y_predictions = logistic_cdf(intercept + slope * features)

Una vez más, el modelo utiliza la optimización para intentar encontrar los mejores valores posibles de intercepción y pendiente.

Dado que el algoritmo de la regresión logística es muy similar a la ecuación de la regresión lineal, forma parte de una familia de modelos denominada "modelos lineales generalizados". Por eso la regresión logística lleva "regresión" en su nombre, aunque sea un modelo de clasificación.

La función sigmoidea se asemeja a una curva en forma de S en la imagen inferior. Toma los valores de entrada numerados reales y los convierte entre 0 y 1 (reduciendo de ambos lados, es decir, los valores negativos a 0 y los positivos muy altos a 1). Además, el umbral de corte es el factor decisivo superpuesto que divide el resultado en categorías o clases cuando se aplica sobre estas probabilidades.

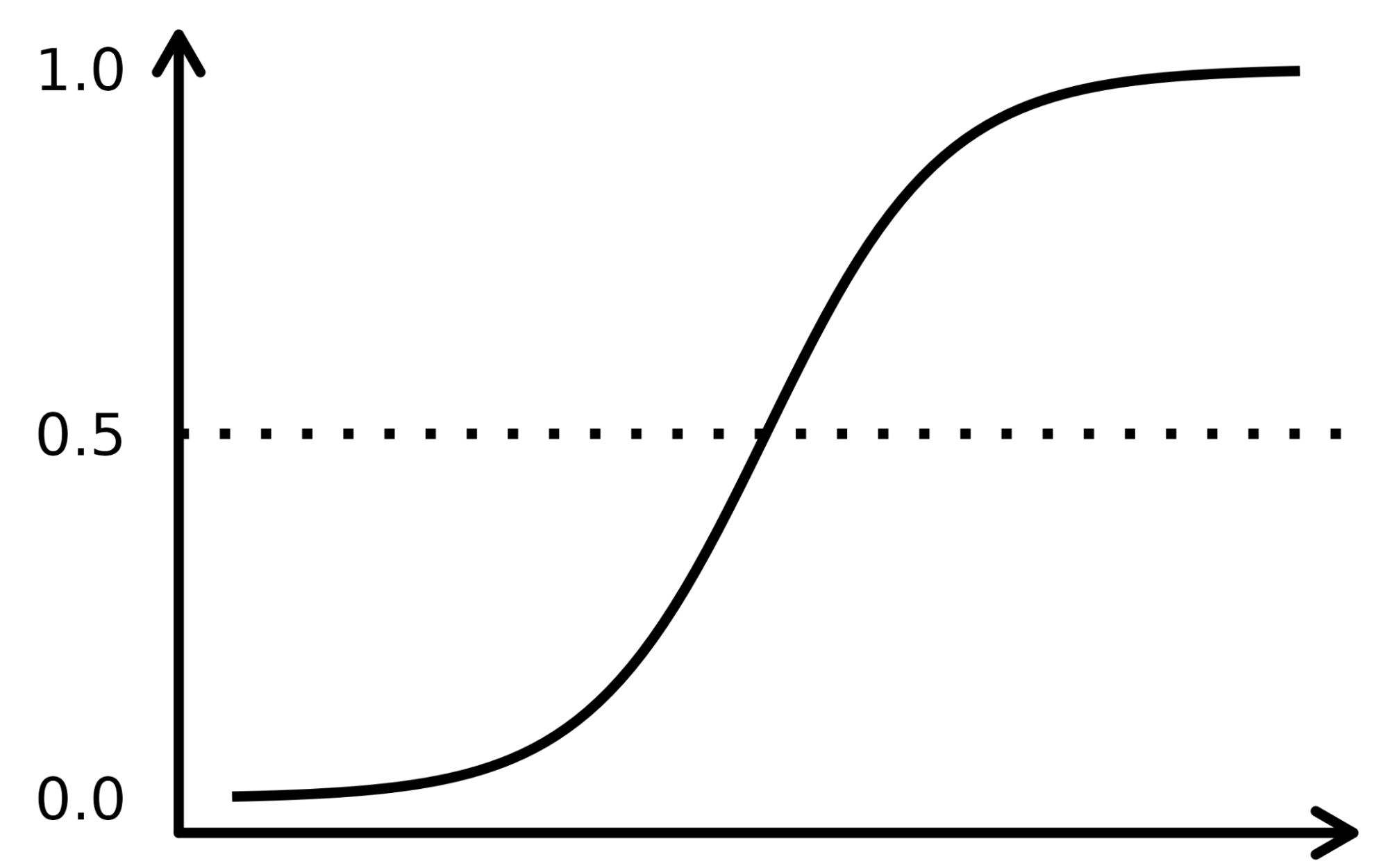
Los conceptos complejos se entienden mejor cuando se explican con ejemplos, así que tomemos una analogía para registrar el funcionamiento del algoritmo LR. Supongamos que el modelo LR se encarga de identificar una transacción fraudulenta examinando varios indicadores de fraude, como la ubicación del usuario, el importe de la compra, la dirección IP, etc. El objetivo es determinar la probabilidad de que una transacción determinada sea legítima o fraudulenta, lo que constituye la variable objetivo.

El modelo asigna pesos a los predictores en función de su impacto en la variable objetivo y los combina para calcular la puntuación normalizada o probabilidad de fraude. 

El conjunto de datos

Utilizaremos un conjunto de datos de una campaña de marketing directo realizada por una entidad bancaria portuguesa mediante llamadas telefónicas. La campaña pretende vender suscripciones de un depósito bancario a plazo representado por la variable y (suscripción o no suscripción). El objetivo del modelo de regresión logística es predecir si un cliente comprará o no una suscripción en función de las variables predictoras, es decir, los atributos del cliente, como la información demográfica.

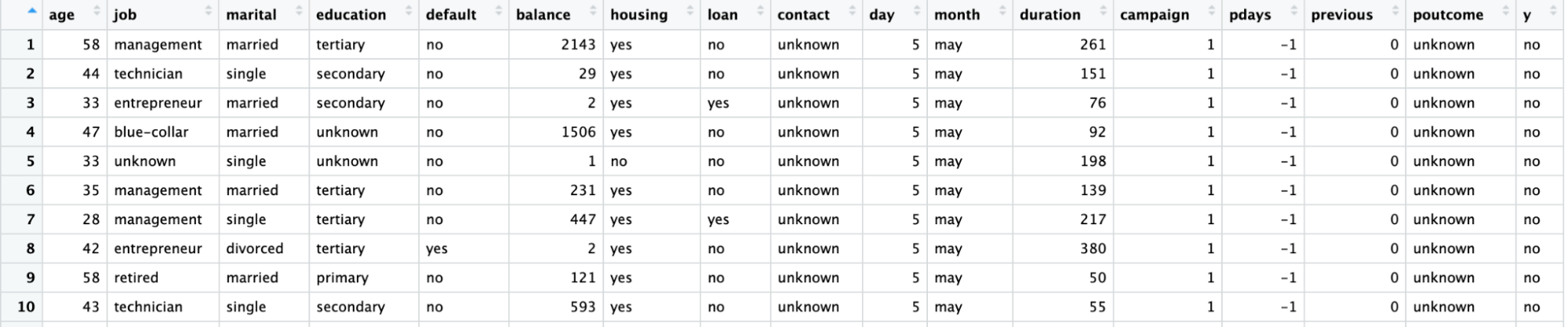
El diccionario de datos de este conjunto de datos y de muchos otros útiles puede consultarse en el sitio web de Datacamp.

Flujo de trabajo de regresión logística

El flujo de trabajo completo del aprendizaje automático se describe en la infografía Guía para principiantes sobre el flujo de trabajo del aprendizaje automático. Aquí nos centraremos en los pasos de preparación de datos y modelado. En concreto, trataremos:

• Dividir los datos en conjuntos de entrenamiento y de prueba
• Ajuste (entrenamiento) del modelo
• Predicciones
• Evaluación del rendimiento del modelo
• Ajuste de hiperparámetros

Paquetes de regresión logística

En R, hay dos flujos de trabajo populares para modelar la regresión logística: base-R y tidymodels.

El flujo de trabajo de modelos base-R es más sencillo e incluye funciones como glm() y summary() para ajustar el modelo y generar un resumen del mismo.

El flujo de trabajo tidymodels permite una gestión más sencilla de varios modelos y una interfaz coherente para trabajar con distintos tipos de modelos.

Este tutorial utilizará el flujo de trabajo tidymodels.

Visualizar los datos

Importa el paquete tidymodels llamando a la función library(). 

El conjunto de datos está en un archivo CSV con formato europeo (comas para los decimales y punto y coma para los separadores). Lo leeremos con read_csv2() del paquete readr. 

Convierta la variable objetivo, y, en una variable factorial para la modelización. 

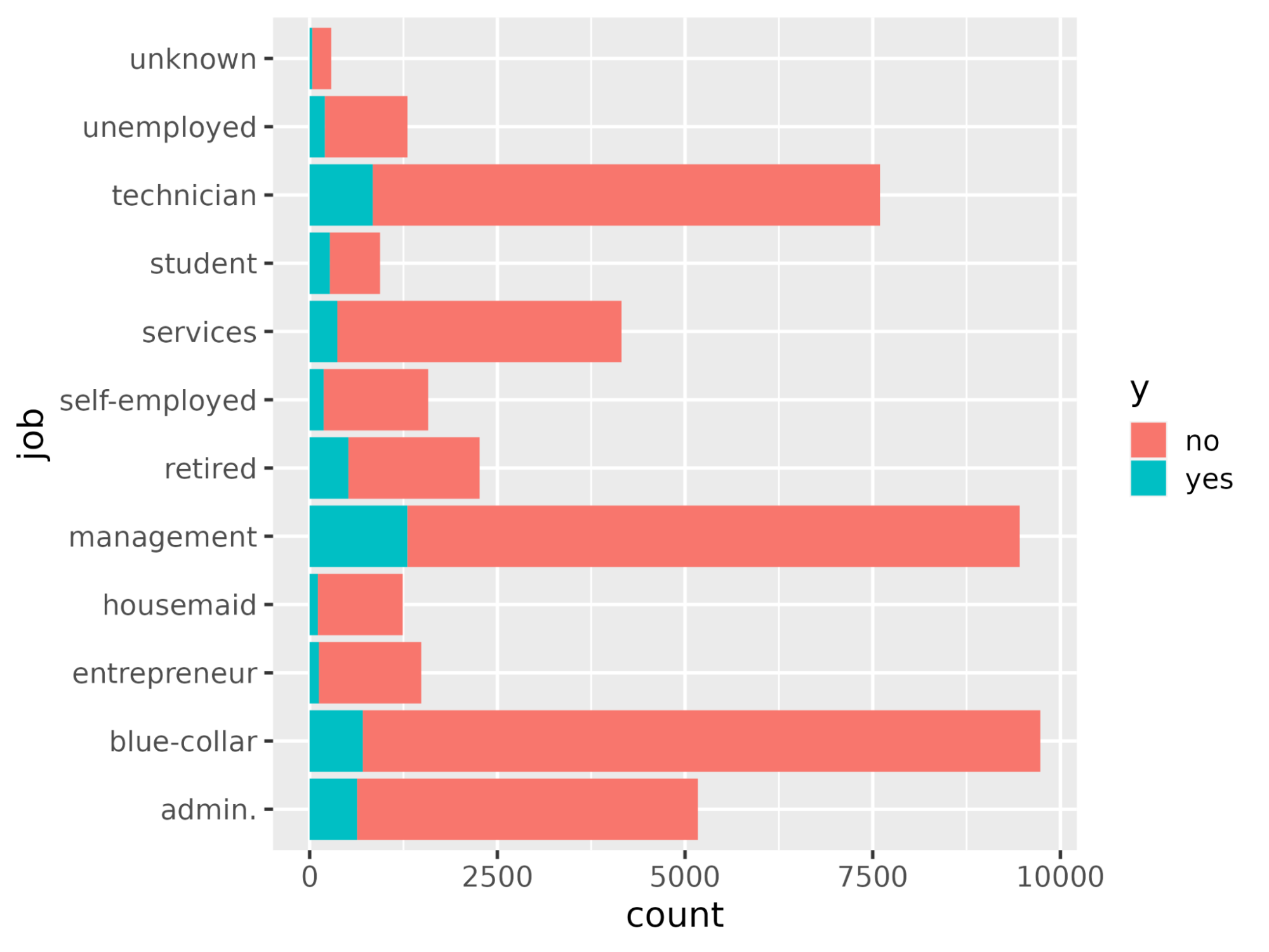
Utilizando la función ggplot(), trace el recuento de cada ocupación laboral con respecto a y.

library(readr)
library(tidymodels)

# Read the dataset and convert the target variable to a factor
bank_df <- read_csv2("bank-full.csv")
bank_df$y = as.factor(bank_df$y)

# Plot job occupation against the target variable
ggplot(bank_df, aes(job, fill = y)) +
    geom_bar() +
    coord_flip()

Dividir los datos

Dividamos el conjunto de datos en un conjunto de entrenamiento para ajustar el modelo y un conjunto de pruebas para evaluar el modelo y asegurarnos de que el modelo así entrenado funciona en un conjunto de datos no visto.

La división de los datos en conjuntos de entrenamiento y prueba puede realizarse utilizando la función initial_split() y el atributo prop que define la proporción de datos de entrenamiento.

# Split data into train and test
set.seed(421)
split <- initial_split(bank_df, prop = 0.8, strata = y)
train <- split %>% 
         training()
test <- split %>% 
        testing()

Ajuste y evaluación del modelo

Para crear el modelo, declare un modelo logistic_reg(). Esto necesita argumentos de mezcla y penalización que controlen la cantidad de regularización. Un valor de mezcla de 1 denota un modelo lasso y 0 denota una regresión ridge. También se permiten valores intermedios. El argumento de la penalización denota la fuerza de la regularización.

Tenga en cuenta que debe pasar números de coma flotante "doble" a la mezcla y la penalización

Establezca el "motor" (el software backend utilizado para ejecutar los cálculos) con set_engine(). Hay varias opciones: El motor por defecto es "glm", que realiza una regresión logística clásica. Los estadísticos suelen preferir este método porque se obtienen valores p para cada coeficiente, lo que facilita la comprensión de la importancia de cada coeficiente.

Aquí utilizaremos el motor "glmnet". Los científicos especializados en aprendizaje automático lo prefieren porque permite la regularización, que puede mejorar las predicciones, sobre todo si se dispone de muchas características. (En Python, el paquete scikit-learn incluye por defecto cierta regularización en la regresión logística).

Llama al método fit() para entrenar el modelo en los datos de entrenamiento creados en el paso anterior. Toma una fórmula como primer argumento. En el lado izquierdo de la fórmula, se utiliza la variable objetivo (en este caso y). En la parte derecha, puede incluir las características que desee. Un punto significa "utilizar todas las variables que no estaban escritas en el lado izquierdo de la fórmula". Para más información sobre la escritura de fórmulas, lea el Tutorial de fórmulas de R.

# Train a logistic regression model
model <- logistic_reg(mixture = double(1), penalty = double(1)) %>%
  set_engine("glmnet") %>%
  set_mode("classification") %>%
  fit(y ~ ., data = train)

# Model summary
tidy(model)

El resultado se muestra a continuación con la columna de estimación que representa los coeficientes del predictor.

# A tibble: 43 × 3
   term              estimate penalty
   <chr>                <dbl>   <dbl>
 1 (Intercept)      -2.59           0
 2 age              -0.000477       0
 3 jobblue-collar   -0.183          0
 4 jobentrepreneur  -0.206          0
 5 jobhousemaid     -0.270          0
 6 jobmanagement    -0.0190         0
 7 jobretired        0.360          0
 8 jobself-employed -0.101          0
 9 jobservices      -0.105          0
10 jobstudent        0.415          0
# ... with 33 more rows
# ℹ Use `print(n = ...)` to see more rows

Predicciones

Realice predicciones sobre los datos de prueba utilizando la función predict(). Puede elegir el tipo de predicciones.

• type = "class" devuelve el valor objetivo más probable para cada observación. En este caso, devolverá un "sí" o un "no" en función de si el modelo piensa que es probable que el cliente suscriba un depósito a plazo o no.
• type = "prob" devuelve la probabilidad de cada valor objetivo para cada observación. En este caso, devolverá la probabilidad de un "sí" y la probabilidad de un "no" (que suman uno para cada observación).

# Class Predictions
pred_class <- predict(model,
                      new_data = test,
                      type = "class")

# Class Probabilities
pred_proba <- predict(model,
                      new_data = test,
                      type = "prob")

Evalúe el modelo utilizando la función accuracy() con el argumento de verdad como y y estime que el valor del argumento son las predicciones del paso anterior.

results <- test %>%
           select(y) %>%
           bind_cols(pred_class, pred_proba)

accuracy(results, truth = y, estimate = .pred_class)

Ajuste de hiperparámetros

En lugar de pasar valores específicos a los argumentos de mezcla y penalización (los "hiperparámetros"), puede optimizar el poder predictivo del modelo ajustándolo. 

La idea es ejecutar el modelo muchas veces con distintos valores de los hiperparámetros y ver cuál ofrece las mejores predicciones.

• En la función logistic_reg(), establezca los argumentos de mezcla y penalización para una llamada a tune().
• Utilice la función grid_regular() para definir una cuadrícula de valores posibles para la mezcla y la penalización.
• La función workflow() crea un objeto para almacenar los detalles del modelo, que es necesario cuando se ejecuta muchas veces. 
• Elija el mejor modelo utilizando la función select_best(). Puede elegir entre una serie de métricas que definen la "mejor". En este caso, utilizaremos la métrica "área bajo la curva de las características operativas del receptor" (ROC AUC).

# Define the logistic regression model with penalty and mixture hyperparameters
log_reg <- logistic_reg(mixture = tune(), penalty = tune(), engine = "glmnet")

# Define the grid search for the hyperparameters
grid <- grid_regular(mixture(), penalty(), levels = c(mixture = 4, penalty = 3))

# Define the workflow for the model
log_reg_wf <- workflow() %>%
  add_model(log_reg) %>%
  add_formula(y ~ .)

# Define the resampling method for the grid search
folds <- vfold_cv(train, v = 5)

# Tune the hyperparameters using the grid search
log_reg_tuned <- tune_grid(
  log_reg_wf,
  resamples = folds,
  grid = grid,
  control = control_grid(save_pred = TRUE)
)

select_best(log_reg_tuned, metric = "roc_auc")

# A tibble: 1 × 3
       penalty mixture .config              
         <dbl>   <dbl> <chr>                
1 0.0000000001       0 Preprocessor1_Model01

Más métricas de evaluación

Utilizar los mejores hiperparámetros:

1. Entrenemos un modelo de regresión logística
2. Utilícelo para generar predicciones sobre el conjunto de pruebas
3. Crear una matriz de confusión utilizando los valores verdaderos, y las estimaciones

# Fit the model using the optimal hyperparameters
log_reg_final <- logistic_reg(penalty = 0.0000000001, mixture = 0) %>%
                 set_engine("glmnet") %>%
                 set_mode("classification") %>%
                 fit(y~., data = train)

# Evaluate the model performance on the testing set
pred_class <- predict(log_reg_final,
                      new_data = test,
                      type = "class")
results <- test %>%
  select(y) %>%
  bind_cols(pred_class, pred_proba)

# Create confusion matrix
conf_mat(results, truth = y,
         estimate = .pred_class)

Truth
Prediction   no  yes
       no  7838  738
       yes  147  320

Puede calcular la precisión (valor predictivo positivo, el número de positivos verdaderos dividido por el número de positivos predichos) con la función precision().

precision(results, truth = y,
          estimate = .pred_class)

# A tibble: 1 × 3
  .metric   .estimator .estimate
  <chr>     <chr>          <dbl>
1 precision binary         0.914

Del mismo modo, puede calcular el recall (sensibilidad, el número de verdaderos positivos dividido por el número de verdaderos positivos) con la función recall().

recall(results, truth = y,
          estimate = .pred_class)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 recall  binary         0.982

Entendamos las variables que influyen en la decisión de compra de suscripciones. En un escenario de regresión logística, los coeficientes deciden lo sensible que es la variable objetivo a los predictores individuales. Cuanto mayor sea el valor de los coeficientes, mayor será su importancia. Ordena las variables en orden descendente del valor absoluto de sus valores de coeficiente y muestra sólo los coeficientes con un valor absoluto superior a 0,5.

coeff <- tidy(log_reg_final) %>% 
  arrange(desc(abs(estimate))) %>% 
  filter(abs(estimate) > 0.5)

# A tibble: 10 × 3
   term            estimate      penalty
   <chr>              <dbl>        <dbl>
 1 (Intercept)       -2.59  0.0000000001
 2 poutcomesuccess    2.08  0.0000000001
 3 monthmar           1.62  0.0000000001
 4 monthoct           1.08  0.0000000001
 5 monthsep           1.03  0.0000000001
 6 contactunknown    -1.01  0.0000000001
 7 monthdec           0.861 0.0000000001
 8 monthjan          -0.820 0.0000000001
 9 housingyes        -0.550 0.0000000001
10 monthnov          -0.517 0.0000000001

Represente gráficamente la importancia de las características mediante la función ggplot().

ggplot(coeff, aes(x = term, y = estimate, fill = term)) + geom_col() + coord_flip()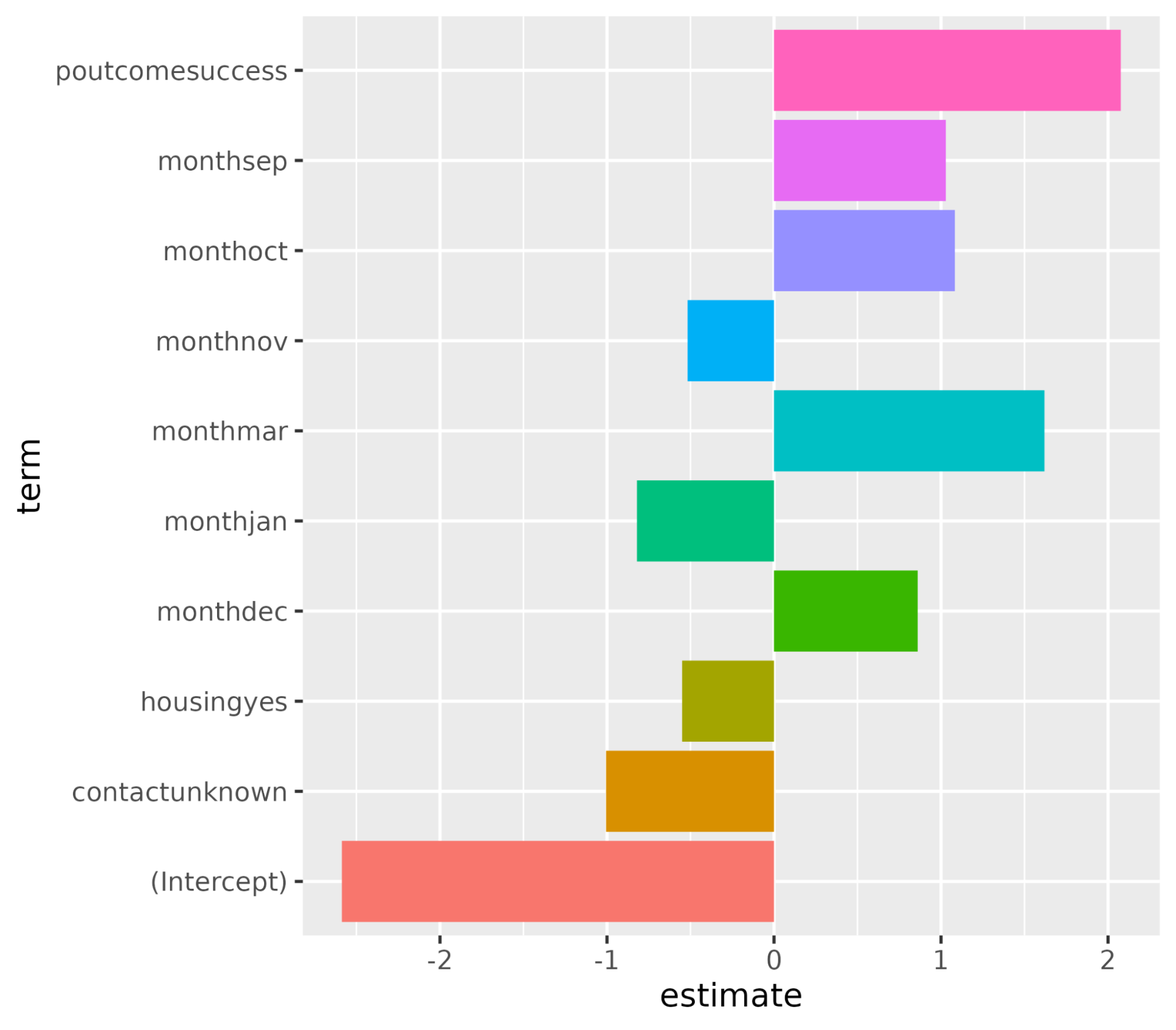

Pase al siguiente nivel

Con esto, hemos llegado al final de este tutorial que demostraba cómo entrenar y evaluar un modelo de regresión logística utilizando el paquete tidymodels. También se explicaba cómo interpretar los resultados del modelo y representarlos gráficamente, como la importancia de los rasgos. 

Si quieres saber más sobre el modelado de modelos de IA con tidymodels, consulta el curso Modelado con tidymodels en R. Para modelar utilizando el enfoque base-R, consulte los cursos Introducción a la regresión en R, Regresión intermedia en R y Modelos lineales generalizados en R.