Logistische Regression in R Tutorial

Die logistische Regression ist ein einfaches, aber leistungsstarkes Modell zur Vorhersage binärer Ergebnisse. Das heißt, ob etwas passieren wird oder nicht. Es ist eine Art Klassifizierungsmodell für überwachtes maschinelles Lernen.

Die logistische Regression wird in fast jeder Branche eingesetzt - im Marketing, im Gesundheitswesen, in den Sozialwissenschaften und in anderen Bereichen - und ist ein unverzichtbarer Bestandteil des Werkzeugkastens eines jeden Datenwissenschaftlers.

Um dieses Tutorial optimal nutzen zu können, brauchst du Grundkenntnisse in R. Außerdem ist es hilfreich, etwas über einen verwandten Modelltyp, die lineare Regression, zu wissen. Lies das Tutorial Lineare Regression in R, um mehr darüber zu erfahren.

Ein Überblick über die logistische Regression

Angenommen, du willst vorhersagen, ob heute ein sonniger Tag wird oder nicht. Es gibt zwei mögliche Ergebnisse: "sonnig" oder "nicht sonnig". Die Ergebnisvariable wird auch als "Zielvariable" oder "abhängige Variable" bezeichnet.

Es gibt viele Variablen, die das Ergebnis beeinflussen können, z. B. die "Temperatur am Vortag", der "Luftdruck" usw. Die Einflussvariablen werden als Merkmale, unabhängige Variablen oder Prädiktoren bezeichnet - alle diese Begriffe bedeuten das Gleiche. 

Andere Beispiele sind, ob ein Kunde dein Produkt kaufen wird oder nicht, ob eine E-Mail Spam ist oder nicht, ob eine Transaktion betrügerisch ist oder nicht und ob ein Medikament einen Patienten heilen wird oder nicht.  

Wie funktioniert die logistische Regression?

Die logistische Regression findet die bestmögliche Übereinstimmung zwischen der Prädiktor- und der Zielvariablen, um die Wahrscheinlichkeit vorherzusagen, dass die Zielvariable zu einer bestimmten Klasse/Kategorie gehört. 

Die lineare Regression versucht, die beste gerade Linie zu finden, die das Ergebnis aus den Merkmalen vorhersagt. Sie bildet eine Gleichung wie

y_predictions = intercept + slope * features

und nutzt die Optimierung, um die bestmöglichen Werte für Achsenabschnitt und Steigung zu finden.

Die logistische Regression funktioniert ähnlich, nur dass sie eine Regression auf die Wahrscheinlichkeiten des Ergebnisses in einer Kategorie durchführt. Sie verwendet eine Sigmoidfunktion (die kumulative Verteilungsfunktion der logistischen Verteilung), um die rechte Seite dieser Gleichung umzuformen.

y_predictions = logistic_cdf(intercept + slope * features)

Auch hier nutzt das Modell die Optimierung, um die bestmöglichen Werte für Achsenabschnitt und Steigung zu finden.

Da der Algorithmus für die logistische Regression der Gleichung für die lineare Regression sehr ähnlich ist, gehört er zu einer Familie von Modellen, die "verallgemeinerte lineare Modelle" genannt werden. Deshalb trägt die logistische Regression "Regression" in ihrem Namen, obwohl sie ein Klassifikationsmodell ist.

Die sigmoide Funktion ähnelt einer S-förmigen Kurve in der Abbildung unten. Er nimmt die reellen numerischen Eingangswerte und wandelt sie zwischen 0 und 1 um (indem er sie von beiden Seiten her verkleinert, d.h. die negativen Werte auf 0 und die sehr hohen positiven auf 1). Darüber hinaus ist die Abschneidegrenze der entscheidende Faktor, der die Ergebnisse in Kategorien oder Klassen einteilt, wenn er auf diese Wahrscheinlichkeiten angewendet wird.

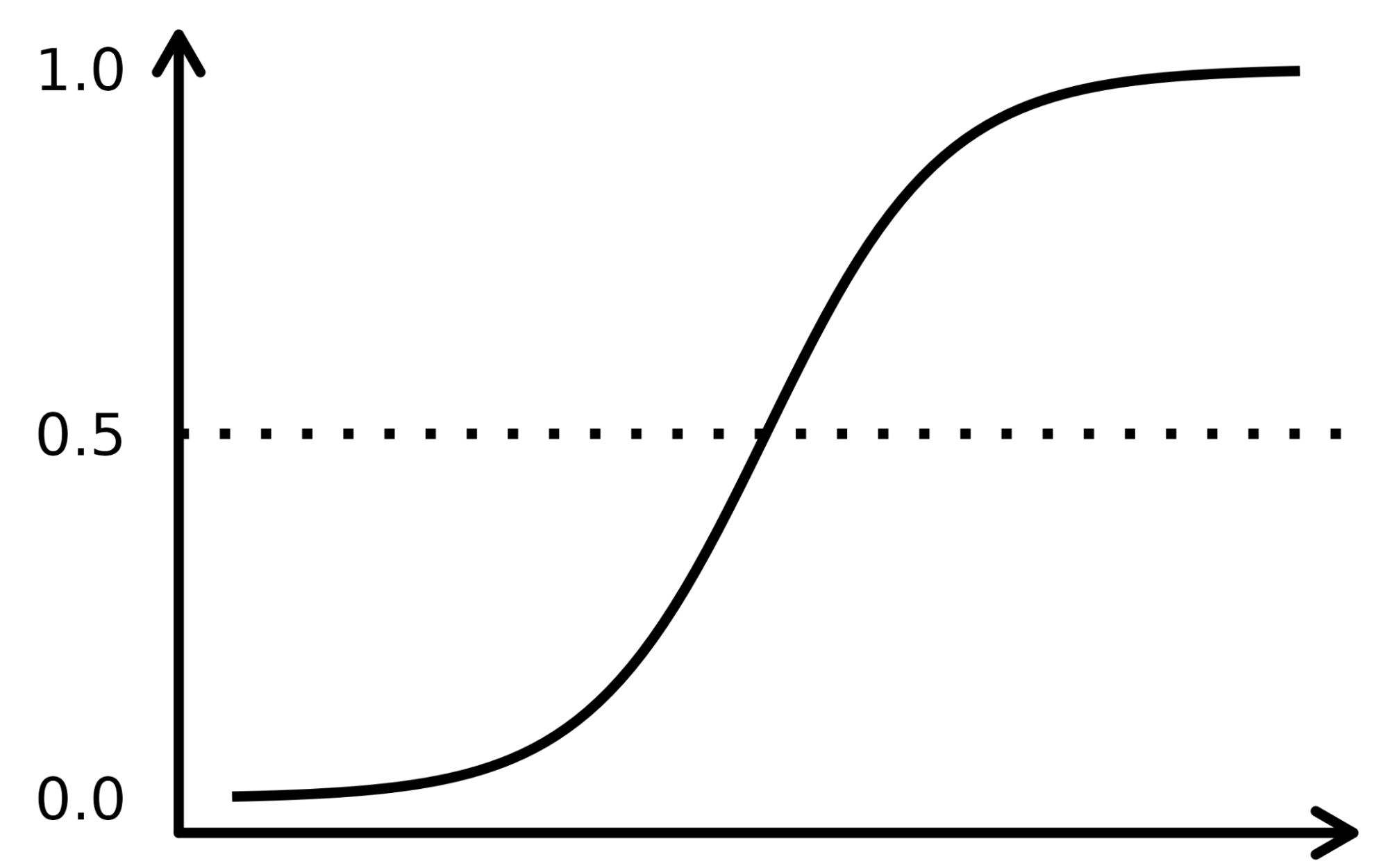
Komplexe Konzepte lassen sich am besten verstehen, wenn sie anhand von Beispielen erklärt werden, also lass uns eine Analogie aufgreifen, um die Funktionsweise des LR-Algorithmus zu erfassen. Nehmen wir an, das LR-Modell hat die Aufgabe, eine betrügerische Transaktion zu identifizieren, indem es mehrere Betrugsindikatoren wie den Standort des Nutzers, den Kaufbetrag, die IP-Adresse usw. untersucht. Das Ziel ist es, die Wahrscheinlichkeit zu bestimmen, ob eine bestimmte Transaktion rechtmäßig oder betrügerisch ist - was die Zielvariable darstellt.

Das Modell gewichtet die Prädiktoren je nach ihrem Einfluss auf die Zielvariable und kombiniert sie, um die normalisierte Punktzahl oder Betrugswahrscheinlichkeit zu berechnen. 

Der Datensatz

Wir verwenden den Datensatz einer Direktmarketing-Kampagne eines portugiesischen Bankinstituts, die Telefonanrufe nutzt. Die Kampagne zielt darauf ab, Abonnements für eine Bank-Festgeldanlage zu verkaufen, die durch die Variable y (Abonnement oder kein Abonnement) dargestellt wird. Ziel des logistischen Regressionsmodells ist es, anhand der Vorhersagevariablen, d.h. der Eigenschaften des Kunden, wie z.B. der demografischen Informationen, vorherzusagen, ob ein Kunde ein Abonnement kaufen würde oder nicht.

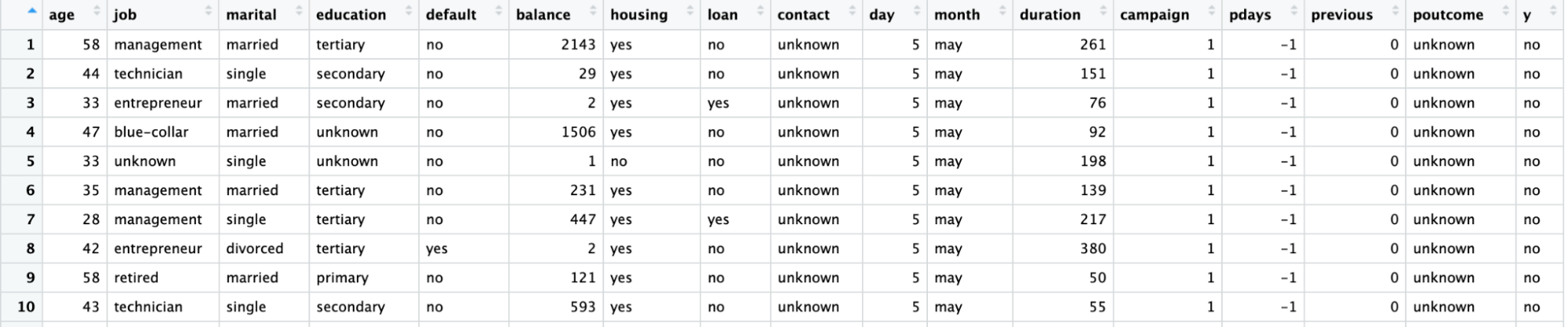
Das Datenwörterbuch für diesen Datensatz und viele andere nützliche Datensätze findest du auf der Website von Datacamp.

Logistische Regression Arbeitsablauf

Der gesamte Workflow des maschinellen Lernens wird in der Infografik A Beginner's Guide to The Machine Learning Workflow beschrieben. Hier konzentrieren wir uns auf die Schritte zur Datenvorbereitung und Modellierung. Wir werden uns insbesondere mit folgenden Themen beschäftigen:

• Aufteilung der Daten in Trainings- und Testgruppen
• Anpassen (Trainieren) des Modells
• Vorhersagen treffen
• Bewertung der Modellleistung
• Hyperparameter-Abstimmung

Logistische Regression Pakete

In R gibt es zwei beliebte Workflows für die Modellierung der logistischen Regression: base-R und tidymodels.

Die Base-R Workflow-Modelle sind einfacher und enthalten Funktionen wie glm() und summary(), um das Modell anzupassen und eine Modellzusammenfassung zu erstellen.

Der tidymodels Workflow ermöglicht eine einfachere Verwaltung mehrerer Modelle und eine einheitliche Schnittstelle für die Arbeit mit verschiedenen Modelltypen.

In diesem Lernprogramm wird der tidymodels Workflow verwendet.

Visualisiere die Daten

Importiere das Paket tidymodels, indem du die Funktion library() aufrufst. 

Der Datensatz liegt in einer CSV-Datei mit europäischer Formatierung vor (Kommas für Dezimalstellen und Semikolons für Trennzeichen). Wir lesen sie mit read_csv2() aus dem readr-Paket. 

Wandle die Zielvariable y in eine Faktorvariable für die Modellierung um. 

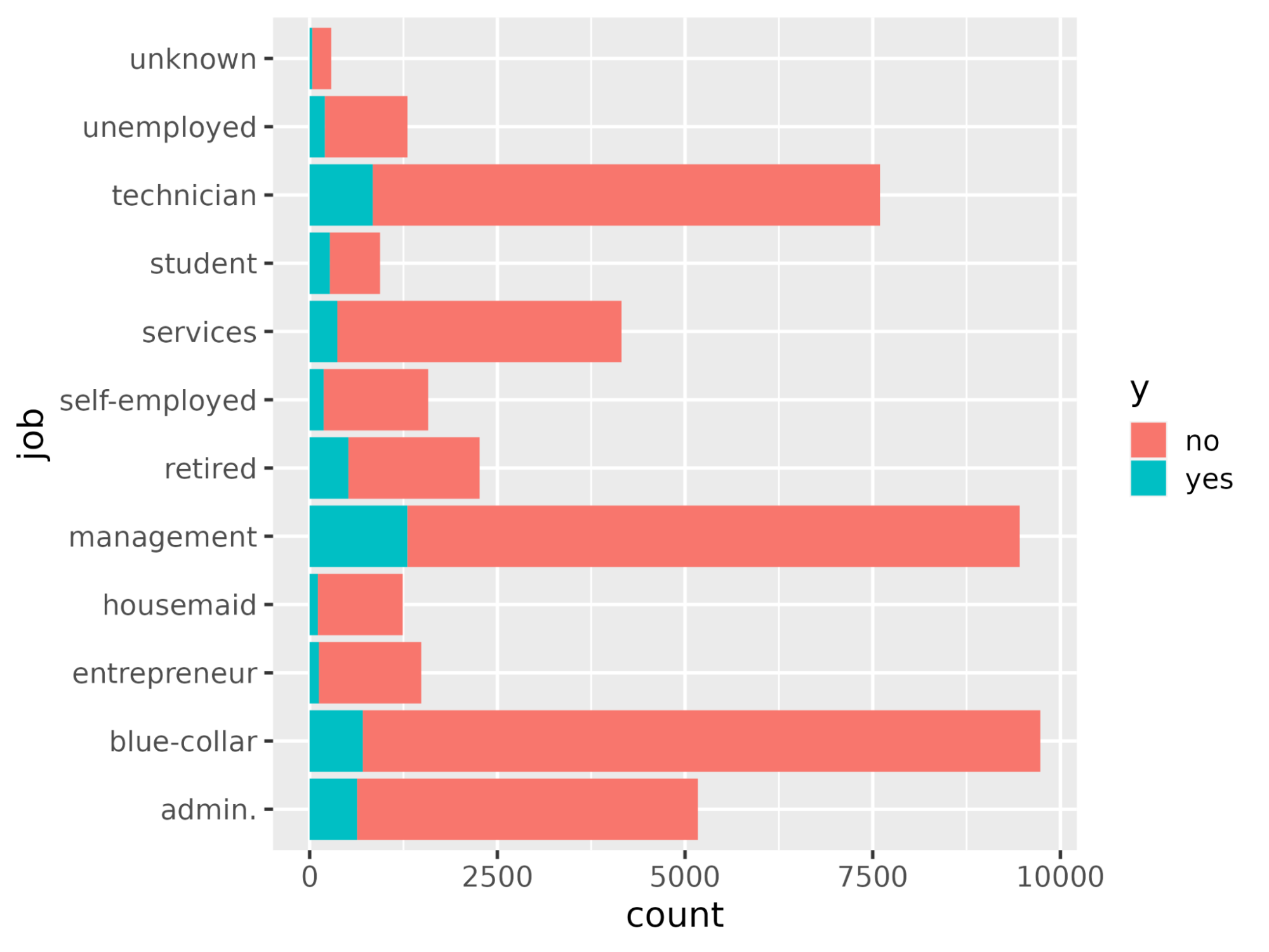
Stelle mit der Funktion ggplot() die Anzahl der einzelnen Berufe in Abhängigkeit von y dar.

library(readr)
library(tidymodels)

# Read the dataset and convert the target variable to a factor
bank_df <- read_csv2("bank-full.csv")
bank_df$y = as.factor(bank_df$y)

# Plot job occupation against the target variable
ggplot(bank_df, aes(job, fill = y)) +
    geom_bar() +
    coord_flip()

Aufteilung der Daten

Wir teilen den Datensatz in einen Trainingsdatensatz für die Anpassung des Modells und einen Testdatensatz für die Evaluierung des Modells auf, um sicherzustellen, dass das so trainierte Modell auch auf einem ungesehenen Datensatz funktioniert.

Die Aufteilung der Daten in Trainings- und Testdaten kann mit der Funktion initial_split() und dem Attribut prop vorgenommen werden, das den Anteil der Trainingsdaten definiert.

# Split data into train and test
set.seed(421)
split <- initial_split(bank_df, prop = 0.8, strata = y)
train <- split %>% 
         training()
test <- split %>% 
        testing()

Anpassen und Auswerten des Modells

Um das Modell zu erstellen, deklarierst du ein logistic_reg()-Modell. Hierfür werden Mischungs- und Strafargumente benötigt, die das Ausmaß der Regularisierung steuern. Ein Mischungswert von 1 steht für ein Lasso-Modell und 0 für eine Ridge-Regression. Es sind auch Werte dazwischen erlaubt. Das Strafargument gibt die Stärke der Regularisierung an.

Beachte, dass du "doppelte" Fließkommazahlen an die Mischung und die Strafe übergeben musst

Setze die "Engine" (die Backend-Software, mit der die Berechnungen durchgeführt werden) mit set_engine(). Es gibt mehrere Möglichkeiten: Die Standard-Engine ist "glm", die eine klassische logistische Regression durchführt. Diese Methode wird oft von Statistikern bevorzugt, weil du p-Werte für jeden Koeffizienten erhältst, was es einfacher macht, die Bedeutung der einzelnen Koeffizienten zu verstehen.

Hier verwenden wir die Engine "glmnet". Diese Methode wird von Wissenschaftlern im Bereich des maschinellen Lernens bevorzugt, weil sie eine Regularisierung ermöglicht, die die Vorhersagen verbessern kann, insbesondere wenn du viele Merkmale hast. (In Python ist das scikit-learn-Paket standardmäßig so eingestellt, dass eine gewisse Regularisierung in der logistischen Regression enthalten ist).

Rufe die fit()-Methode auf, um das Modell anhand der im vorherigen Schritt erstellten Trainingsdaten zu trainieren. Das erste Argument für diese Funktion ist eine Formel. Auf der linken Seite der Formel verwendest du die Zielvariable (in diesem Fall y). Auf der rechten Seite kannst du jede beliebige Funktion einfügen, die du möchtest. Ein Punkt bedeutet: "Verwende alle Variablen, die nicht auf der linken Seite der Formel geschrieben wurden. Weitere Informationen zum Schreiben von Formeln findest du im R Formula Tutorial.

# Train a logistic regression model
model <- logistic_reg(mixture = double(1), penalty = double(1)) %>%
  set_engine("glmnet") %>%
  set_mode("classification") %>%
  fit(y ~ ., data = train)

# Model summary
tidy(model)

Die Ausgabe ist unten dargestellt, wobei die Spalte Schätzung die Koeffizienten des Prädiktors darstellt.

# A tibble: 43 × 3
   term              estimate penalty
   <chr>                <dbl>   <dbl>
 1 (Intercept)      -2.59           0
 2 age              -0.000477       0
 3 jobblue-collar   -0.183          0
 4 jobentrepreneur  -0.206          0
 5 jobhousemaid     -0.270          0
 6 jobmanagement    -0.0190         0
 7 jobretired        0.360          0
 8 jobself-employed -0.101          0
 9 jobservices      -0.105          0
10 jobstudent        0.415          0
# ... with 33 more rows
# ℹ Use `print(n = ...)` to see more rows

Vorhersagen treffen

Mache Vorhersagen für die Testdaten mit der Funktion predict(). Du hast die Wahl der Art der Vorhersagen.

• type = "class" gibt den wahrscheinlichsten Zielwert für jede Beobachtung zurück. Hier wird ein "Ja" oder ein "Nein" zurückgegeben, je nachdem, ob das Modell davon ausgeht, dass der Kunde ein Festgeld zeichnen wird oder nicht.
• type = "prob" gibt die Wahrscheinlichkeit jedes Zielwerts für jede Beobachtung zurück. Hier wird die Wahrscheinlichkeit für ein "Ja" und die Wahrscheinlichkeit für ein "Nein" zurückgegeben (die sich für jede Beobachtung zu eins addieren).

# Class Predictions
pred_class <- predict(model,
                      new_data = test,
                      type = "class")

# Class Probabilities
pred_proba <- predict(model,
                      new_data = test,
                      type = "prob")

Bewerte das Modell mit der Funktion accuracy() mit dem Wahrheitsargument y und schätze den Wert des Arguments als die Vorhersagen aus dem vorherigen Schritt.

results <- test %>%
           select(y) %>%
           bind_cols(pred_class, pred_proba)

accuracy(results, truth = y, estimate = .pred_class)

Hyperparameter-Abstimmung

Anstatt den Argumenten für Mischung und Strafe (den "Hyperparametern") bestimmte Werte zu geben, kannst du die Vorhersagekraft des Modells optimieren, indem du es abstimmst. 

Die Idee ist, dass du das Modell viele Male mit verschiedenen Werten der Hyperparameter durchführst und siehst, welcher Wert die besten Vorhersagen liefert.

• Setze in der Funktion logistic_reg() die Mixtur- und Strafargumente für einen Aufruf von tune().
• Verwende die Funktion grid_regular(), um ein Raster möglicher Werte für Mischung und Strafe zu definieren.
• Die Funktion workflow() erstellt ein Objekt, um die Details des Modells zu speichern, was nötig ist, wenn du es viele Male ausführst. 
• Wähle das beste Modell mit der Funktion select_best() aus. Du kannst aus einer Reihe von Metriken die "beste" auswählen. Hier verwenden wir die Kennzahl "Receiver Operating Characteristic Area under the Curve" (ROC AUC).

# Define the logistic regression model with penalty and mixture hyperparameters
log_reg <- logistic_reg(mixture = tune(), penalty = tune(), engine = "glmnet")

# Define the grid search for the hyperparameters
grid <- grid_regular(mixture(), penalty(), levels = c(mixture = 4, penalty = 3))

# Define the workflow for the model
log_reg_wf <- workflow() %>%
  add_model(log_reg) %>%
  add_formula(y ~ .)

# Define the resampling method for the grid search
folds <- vfold_cv(train, v = 5)

# Tune the hyperparameters using the grid search
log_reg_tuned <- tune_grid(
  log_reg_wf,
  resamples = folds,
  grid = grid,
  control = control_grid(save_pred = TRUE)
)

select_best(log_reg_tuned, metric = "roc_auc")

# A tibble: 1 × 3
       penalty mixture .config              
         <dbl>   <dbl> <chr>                
1 0.0000000001       0 Preprocessor1_Model01

Weitere Bewertungsmetriken

Verwendung der besten Hyperparameter:

1. Lass uns ein logistisches Regressionsmodell trainieren
2. Nutze sie, um Vorhersagen für die Testmenge zu erstellen
3. Erstelle eine Konfusionsmatrix mit den wahren Werten und den Schätzungen

# Fit the model using the optimal hyperparameters
log_reg_final <- logistic_reg(penalty = 0.0000000001, mixture = 0) %>%
                 set_engine("glmnet") %>%
                 set_mode("classification") %>%
                 fit(y~., data = train)

# Evaluate the model performance on the testing set
pred_class <- predict(log_reg_final,
                      new_data = test,
                      type = "class")
results <- test %>%
  select(y) %>%
  bind_cols(pred_class, pred_proba)

# Create confusion matrix
conf_mat(results, truth = y,
         estimate = .pred_class)

Truth
Prediction   no  yes
       no  7838  738
       yes  147  320

Mit der Funktion precision() kannst du die Genauigkeit (positiver Vorhersagewert, d.h. die Anzahl der wahren Positiven geteilt durch die Anzahl der vorhergesagten Positiven) berechnen.

precision(results, truth = y,
          estimate = .pred_class)

# A tibble: 1 × 3
  .metric   .estimator .estimate
  <chr>     <chr>          <dbl>
1 precision binary         0.914

Auf ähnliche Weise kannst du mit der recall()-Funktion den Recall (die Sensitivität, also die Anzahl der echten Positiven geteilt durch die Anzahl der tatsächlichen Positiven) berechnen.

recall(results, truth = y,
          estimate = .pred_class)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 recall  binary         0.982

Wir wollen die Variablen verstehen, die die Entscheidung für ein Abonnement beeinflussen. In einem logistischen Regressionsszenario entscheiden die Koeffizienten darüber, wie empfindlich die Zielvariable auf die einzelnen Prädiktoren reagiert. Je höher der Wert der Koeffizienten, desto größer ist ihre Bedeutung. Sortiere die Variablen in absteigender Reihenfolge nach dem absoluten Wert ihrer Koeffizientenwerte und zeige nur die Koeffizienten mit einem absoluten Wert größer als 0,5 an.

coeff <- tidy(log_reg_final) %>% 
  arrange(desc(abs(estimate))) %>% 
  filter(abs(estimate) > 0.5)

# A tibble: 10 × 3
   term            estimate      penalty
   <chr>              <dbl>        <dbl>
 1 (Intercept)       -2.59  0.0000000001
 2 poutcomesuccess    2.08  0.0000000001
 3 monthmar           1.62  0.0000000001
 4 monthoct           1.08  0.0000000001
 5 monthsep           1.03  0.0000000001
 6 contactunknown    -1.01  0.0000000001
 7 monthdec           0.861 0.0000000001
 8 monthjan          -0.820 0.0000000001
 9 housingyes        -0.550 0.0000000001
10 monthnov          -0.517 0.0000000001

Stelle die Bedeutung der Merkmale mit der Funktion ggplot() dar.

ggplot(coeff, aes(x = term, y = estimate, fill = term)) + geom_col() + coord_flip()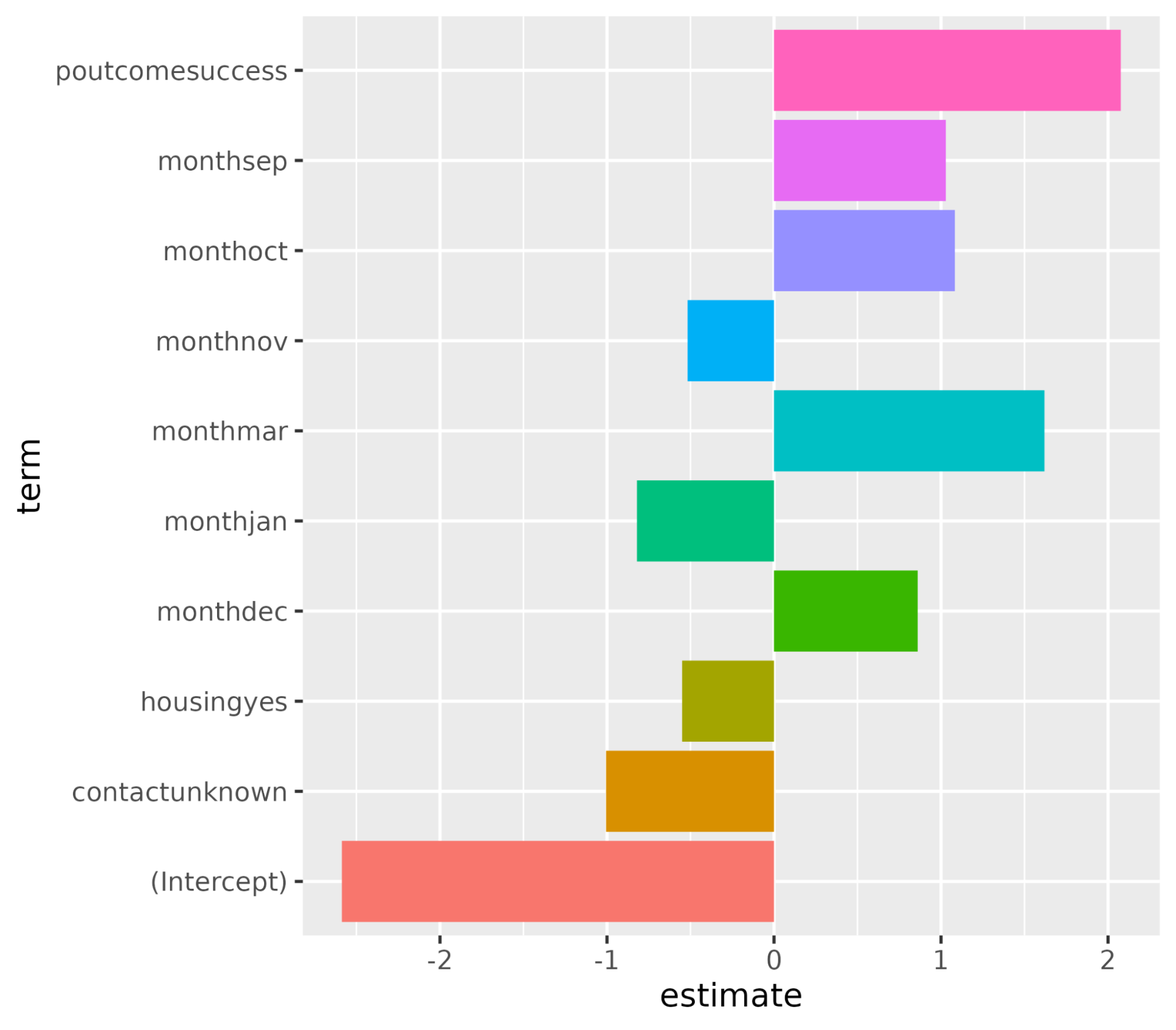

Bring es auf die nächste Stufe

Damit sind wir am Ende dieses Tutorials angelangt, das gezeigt hat, wie man mit dem Paket tidymodels ein logistisches Regressionsmodell trainiert und auswertet. Es wurde auch erklärt, wie man die Modellergebnisse interpretiert und wie man sie als Merkmalsbedeutung darstellt. 

Wenn du mehr über die Modellierung von KI-Modellen mit Tidymodels erfahren möchtest, schau dir den Kurs Modellierung mit Tidymodels in R an. Für die Modellierung mit dem Base-R-Ansatz, schau dir die Kurse Einführung in die Regression in R, Intermediate Regression in R und Generalized Linear Models in R an.