Tutorial de regressão logística no R

A regressão logística é um modelo simples, mas poderoso, para prever resultados binários. Ou seja, se algo vai acontecer ou não. É um tipo de modelo de classificação para aprendizado de máquina supervisionado.

A regressão logística é usada em quase todos os setores - marketing, saúde, ciências sociais e outros - e é uma parte essencial do kit de ferramentas de qualquer cientista de dados.

Para aproveitar ao máximo este tutorial, você precisa ter um conhecimento básico de R. Também é útil conhecer um tipo de modelo relacionado, a regressão linear. Leia o tutorial Regressão linear em R para saber mais sobre isso.

Uma visão geral da regressão logística

Suponha que você queira prever se hoje será um dia ensolarado ou não. Há dois resultados possíveis: "ensolarado" ou "não ensolarado". A variável de resultado também é conhecida como "variável-alvo" ou "variável dependente".

Há muitas variáveis que podem influenciar o resultado, como "temperatura no dia anterior", "pressão do ar" etc. As variáveis de influência são conhecidas como características, variáveis independentes ou preditores - todos esses termos significam a mesma coisa. 

Outros exemplos incluem se um cliente comprará seu produto ou não, se um e-mail é spam ou não, se uma transação é fraudulenta ou não e se um medicamento curará um paciente ou não.  

Como funciona a regressão logística?

A regressão logística encontra o melhor ajuste possível entre as variáveis preditoras e de destino para prever a probabilidade de a variável de destino pertencer a uma classe/categoria rotulada. 

A regressão linear tenta encontrar a melhor linha reta que prevê o resultado a partir dos recursos. Ele forma uma equação como

y_predictions = intercept + slope * features

e usa a otimização para tentar encontrar os melhores valores possíveis de interceptação e inclinação.

A regressão logística funciona de forma semelhante, exceto pelo fato de que ela realiza a regressão nas probabilidades de o resultado ser uma categoria. Ele usa uma função sigmoide (a função de distribuição cumulativa da distribuição logística) para transformar o lado direito dessa equação.

y_predictions = logistic_cdf(intercept + slope * features)

Novamente, o modelo usa a otimização para tentar encontrar os melhores valores possíveis de interceptação e inclinação.

Como o algoritmo da regressão logística é muito semelhante à equação da regressão linear, ele faz parte de uma família de modelos chamada "modelos lineares generalizados". É por isso que a regressão logística tem "regressão" em seu nome, embora seja um modelo de classificação.

A função sigmoide se assemelha a uma curva em forma de S na imagem abaixo. Ele pega os valores de entrada numerados reais e os converte entre 0 e 1 (reduzindo-os de ambos os lados, ou seja, os valores negativos para 0 e os positivos muito altos para 1). Além disso, o limite de corte é o fator decisivo de sobreposição que divide o resultado em categorias ou classes quando aplicado sobre essas probabilidades.

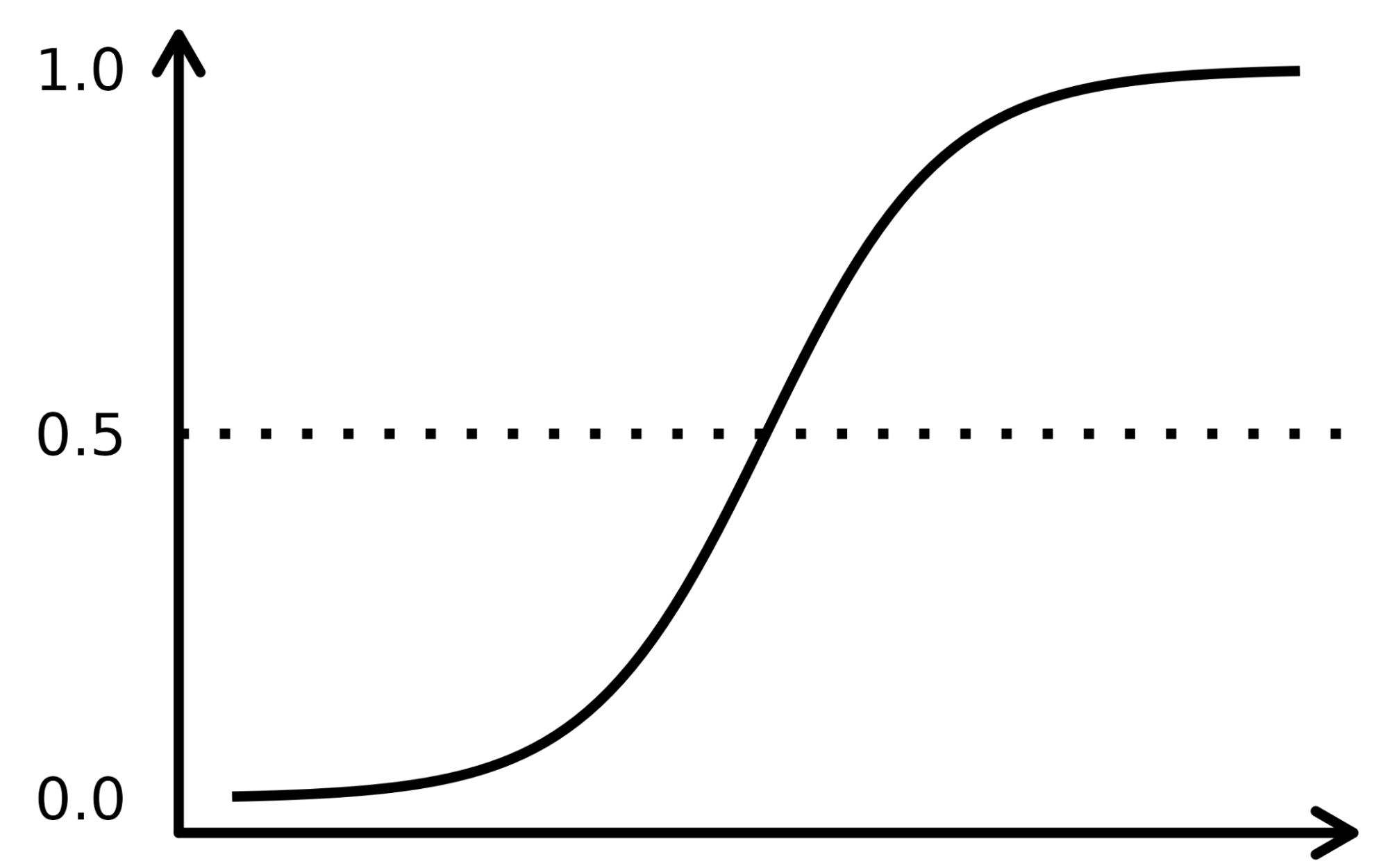
Os conceitos complexos são mais bem compreendidos quando explicados com exemplos, portanto, vamos usar uma analogia para registrar o funcionamento do algoritmo de LR. Vamos supor que o modelo de LR tenha a tarefa de identificar uma transação fraudulenta examinando vários indicadores de fraude, como a localização do usuário, o valor da compra, o endereço IP etc. O objetivo é determinar a probabilidade de uma determinada transação ser legítima ou fraudulenta, o que constitui a variável-alvo.

O modelo atribui pesos aos preditores com base em como eles afetam a variável-alvo e os combina para calcular a pontuação normalizada ou a probabilidade de fraude. 

O conjunto de dados

Usaríamos um conjunto de dados de campanha de marketing direto de uma instituição bancária portuguesa usando chamadas telefônicas. O objetivo da campanha é vender assinaturas de um depósito bancário a prazo representado pela variável y (assinatura ou não assinatura). O objetivo do modelo de regressão logística é prever se um cliente compraria ou não uma assinatura com base nas variáveis preditoras, também conhecidas como atributos do cliente, como informações demográficas.

O dicionário de dados para esse conjunto de dados e muitos outros conjuntos de dados úteis pode ser encontrado no site do Datacamp.

Fluxo de trabalho de regressão logística

O fluxo de trabalho completo de aprendizado de máquina é abordado no infográfico Guia para iniciantes do fluxo de trabalho de aprendizado de máquina. Aqui, vamos nos concentrar nas etapas de preparação e modelagem de dados. Em particular, abordaremos:

• Dividir os dados em conjuntos de treinamento e teste
• Ajuste (treinamento) do modelo
• Fazendo previsões
• Avaliação do desempenho do modelo
• Ajuste de hiperparâmetros

Pacotes de regressão logística

No R, há dois fluxos de trabalho populares para modelar a regressão logística: base-R e tidymodels.

Os modelos de fluxo de trabalho base-R são mais simples e incluem funções como glm() e summary() para ajustar o modelo e gerar um resumo do modelo.

O fluxo de trabalho tidymodels permite o gerenciamento mais fácil de vários modelos e uma interface consistente para trabalhar com diferentes tipos de modelos.

Este tutorial usará o fluxo de trabalho tidymodels.

Visualize os dados

Importe o pacote tidymodels chamando a função library(). 

O conjunto de dados está em um arquivo CSV com formatação no estilo europeu (vírgulas para casas decimais e ponto e vírgula para separadores). Nós o leremos com read_csv2() do pacote readr. 

Converta a variável de destino, y, em uma variável de fator para modelagem. 

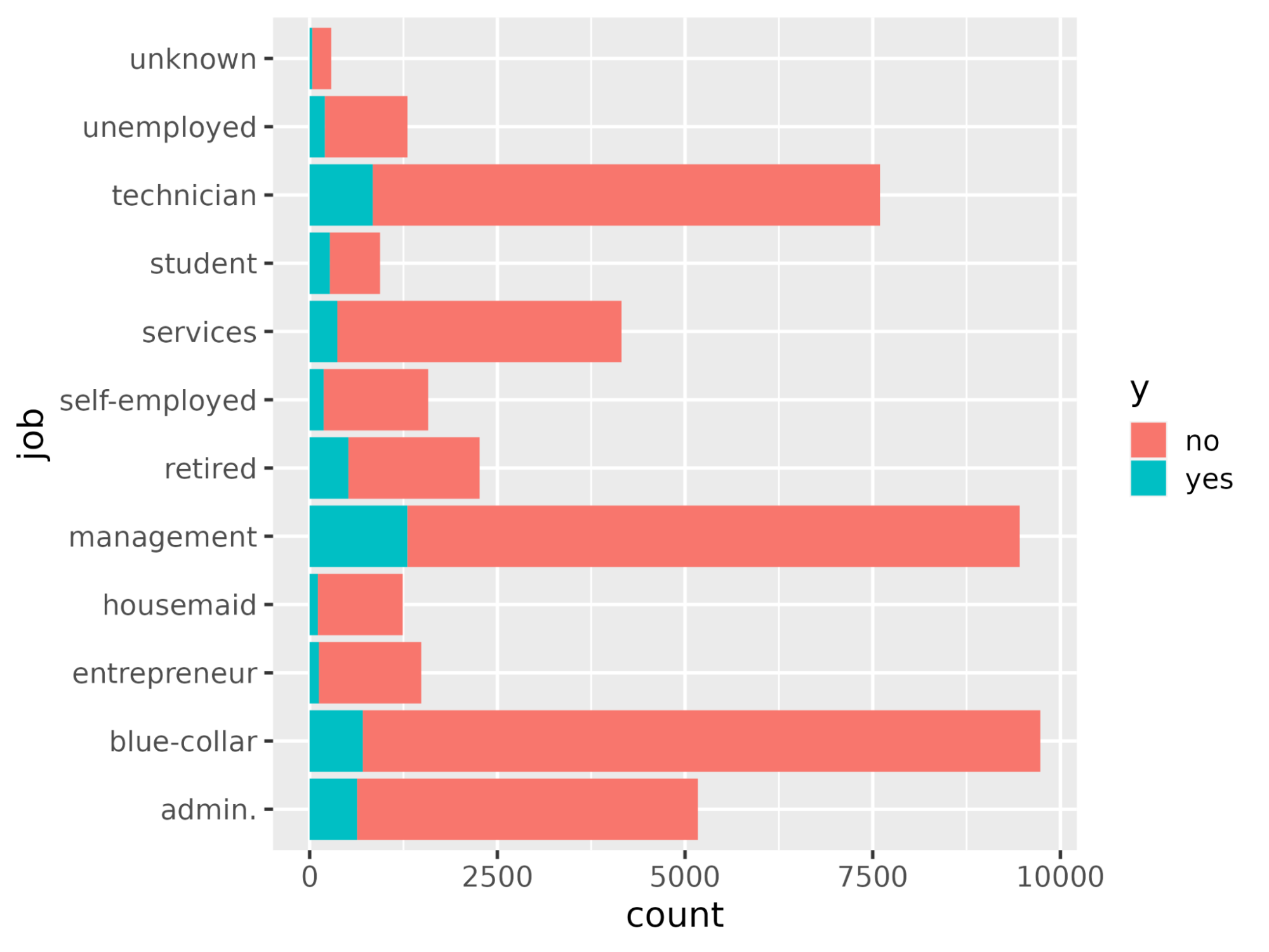
Usando a função ggplot(), desenhe a contagem de cada ocupação de trabalho em relação a y.

library(readr)
library(tidymodels)

# Read the dataset and convert the target variable to a factor
bank_df <- read_csv2("bank-full.csv")
bank_df$y = as.factor(bank_df$y)

# Plot job occupation against the target variable
ggplot(bank_df, aes(job, fill = y)) +
    geom_bar() +
    coord_flip()

Dividindo os dados

Vamos dividir o conjunto de dados em um conjunto de treinamento para ajustar o modelo e um conjunto de teste para avaliação do modelo, a fim de garantir que o modelo assim treinado funcione em um conjunto de dados não visto.

A divisão dos dados em conjuntos de treinamento e teste pode ser feita usando a função initial_split() e o atributo prop que define a proporção dos dados de treinamento.

# Split data into train and test
set.seed(421)
split <- initial_split(bank_df, prop = 0.8, strata = y)
train <- split %>% 
         training()
test <- split %>% 
        testing()

Ajuste e avaliação do modelo

Para criar o modelo, declare um modelo logistic_reg(). Isso requer argumentos de mistura e penalidade que controlam a quantidade de regularização. Um valor de mistura de 1 indica um modelo de laço e 0 indica uma regressão de cumeeira. Valores intermediários também são permitidos. O argumento de penalidade indica a força da regularização.

Observe que você precisa passar números de ponto flutuante "duplo" para a mistura e a penalidade

Defina o "mecanismo" (o software de back-end usado para executar os cálculos) com set_engine(). Há várias opções: O mecanismo padrão é o "glm", que executa uma regressão logística clássica. Isso geralmente é preferido pelos estatísticos porque você obtém valores p para cada coeficiente, o que facilita a compreensão da importância de cada coeficiente.

Aqui, usaremos o mecanismo "glmnet". Isso é preferido pelos cientistas de aprendizado de máquina porque permite a regularização, que pode melhorar as previsões, principalmente se você tiver muitos recursos. (Em Python, o pacote scikit-learn tem como padrão a inclusão de alguma regularização na regressão logística).

Chame o método fit() para treinar o modelo nos dados de treinamento criados na etapa anterior. Recebe uma fórmula como seu primeiro argumento. No lado esquerdo da fórmula, você usa a variável de destino (nesse caso, y). No lado direito, você pode incluir os recursos que desejar. Um ponto final significa "use todas as variáveis que não foram escritas no lado esquerdo da fórmula". Para obter mais informações sobre como escrever fórmulas, leia o Tutorial de fórmulas do R.

# Train a logistic regression model
model <- logistic_reg(mixture = double(1), penalty = double(1)) %>%
  set_engine("glmnet") %>%
  set_mode("classification") %>%
  fit(y ~ ., data = train)

# Model summary
tidy(model)

O resultado é mostrado abaixo, com a coluna de estimativa representando os coeficientes do preditor.

# A tibble: 43 × 3
   term              estimate penalty
   <chr>                <dbl>   <dbl>
 1 (Intercept)      -2.59           0
 2 age              -0.000477       0
 3 jobblue-collar   -0.183          0
 4 jobentrepreneur  -0.206          0
 5 jobhousemaid     -0.270          0
 6 jobmanagement    -0.0190         0
 7 jobretired        0.360          0
 8 jobself-employed -0.101          0
 9 jobservices      -0.105          0
10 jobstudent        0.415          0
# ... with 33 more rows
# ℹ Use `print(n = ...)` to see more rows

Fazendo previsões

Faça previsões sobre os dados de teste usando a função predict(). Você pode escolher o tipo de previsão.

• type = "class" retorna o valor-alvo mais provável para cada observação. Aqui, ele retornará um "sim" ou um "não", dependendo se o modelo acha que o cliente provavelmente assinará um depósito a prazo ou não.
• type = "prob" retorna a probabilidade de cada valor-alvo para cada observação. Aqui, ele retornará a probabilidade de um "sim" e a probabilidade de um "não" (que somam um para cada observação).

# Class Predictions
pred_class <- predict(model,
                      new_data = test,
                      type = "class")

# Class Probabilities
pred_proba <- predict(model,
                      new_data = test,
                      type = "prob")

Avalie o modelo usando a função accuracy() com o argumento verdadeiro como y e estime o valor do argumento como sendo as previsões da etapa anterior.

results <- test %>%
           select(y) %>%
           bind_cols(pred_class, pred_proba)

accuracy(results, truth = y, estimate = .pred_class)

Ajuste de hiperparâmetros

Em vez de passar valores específicos para os argumentos de mistura e penalidade (os "hiperparâmetros"), você pode otimizar a capacidade de previsão do modelo ajustando-o. 

A ideia é que você execute o modelo várias vezes com valores diferentes dos hiperparâmetros e veja qual deles fornece as melhores previsões.

• Na função logistic_reg(), defina os argumentos de mistura e penalidade para uma chamada a tune().
• Use a função grid_regular() para definir uma grade de valores possíveis para mistura e penalidade.
• A função workflow() cria um objeto para armazenar os detalhes do modelo, o que é necessário quando você o executa várias vezes. 
• Escolha o melhor modelo usando a função select_best(). Você pode escolher entre uma variedade de métricas que definem a "melhor". Aqui, usaremos a métrica "área sob a curva da característica de operação do receptor" (ROC AUC).

# Define the logistic regression model with penalty and mixture hyperparameters
log_reg <- logistic_reg(mixture = tune(), penalty = tune(), engine = "glmnet")

# Define the grid search for the hyperparameters
grid <- grid_regular(mixture(), penalty(), levels = c(mixture = 4, penalty = 3))

# Define the workflow for the model
log_reg_wf <- workflow() %>%
  add_model(log_reg) %>%
  add_formula(y ~ .)

# Define the resampling method for the grid search
folds <- vfold_cv(train, v = 5)

# Tune the hyperparameters using the grid search
log_reg_tuned <- tune_grid(
  log_reg_wf,
  resamples = folds,
  grid = grid,
  control = control_grid(save_pred = TRUE)
)

select_best(log_reg_tuned, metric = "roc_auc")

# A tibble: 1 × 3
       penalty mixture .config              
         <dbl>   <dbl> <chr>                
1 0.0000000001       0 Preprocessor1_Model01

Mais métricas de avaliação

Usando os melhores hiperparâmetros:

1. Vamos treinar um modelo de regressão logística
2. Use-o para gerar previsões no conjunto de teste
3. Crie uma matriz de confusão usando os valores reais e as estimativas

# Fit the model using the optimal hyperparameters
log_reg_final <- logistic_reg(penalty = 0.0000000001, mixture = 0) %>%
                 set_engine("glmnet") %>%
                 set_mode("classification") %>%
                 fit(y~., data = train)

# Evaluate the model performance on the testing set
pred_class <- predict(log_reg_final,
                      new_data = test,
                      type = "class")
results <- test %>%
  select(y) %>%
  bind_cols(pred_class, pred_proba)

# Create confusion matrix
conf_mat(results, truth = y,
         estimate = .pred_class)

Truth
Prediction   no  yes
       no  7838  738
       yes  147  320

Você pode calcular a precisão (valor preditivo positivo, o número de positivos verdadeiros dividido pelo número de positivos previstos) com a função precision().

precision(results, truth = y,
          estimate = .pred_class)

# A tibble: 1 × 3
  .metric   .estimator .estimate
  <chr>     <chr>          <dbl>
1 precision binary         0.914

Da mesma forma, você pode calcular a recuperação (sensibilidade, o número de positivos verdadeiros dividido pelo número de positivos reais) com a função recall().

recall(results, truth = y,
          estimate = .pred_class)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 recall  binary         0.982

Vamos entender as variáveis que afetam a decisão de compra de assinaturas. Em um cenário de regressão logística, os coeficientes decidem o quanto a variável-alvo é sensível aos preditores individuais. Quanto maior for o valor dos coeficientes, maior será sua importância. Classifique as variáveis em ordem decrescente do valor absoluto de seus valores de coeficiente e exiba somente os coeficientes com valor absoluto maior que 0,5.

coeff <- tidy(log_reg_final) %>% 
  arrange(desc(abs(estimate))) %>% 
  filter(abs(estimate) > 0.5)

# A tibble: 10 × 3
   term            estimate      penalty
   <chr>              <dbl>        <dbl>
 1 (Intercept)       -2.59  0.0000000001
 2 poutcomesuccess    2.08  0.0000000001
 3 monthmar           1.62  0.0000000001
 4 monthoct           1.08  0.0000000001
 5 monthsep           1.03  0.0000000001
 6 contactunknown    -1.01  0.0000000001
 7 monthdec           0.861 0.0000000001
 8 monthjan          -0.820 0.0000000001
 9 housingyes        -0.550 0.0000000001
10 monthnov          -0.517 0.0000000001

Plote a importância do recurso usando a função ggplot().

ggplot(coeff, aes(x = term, y = estimate, fill = term)) + geom_col() + coord_flip()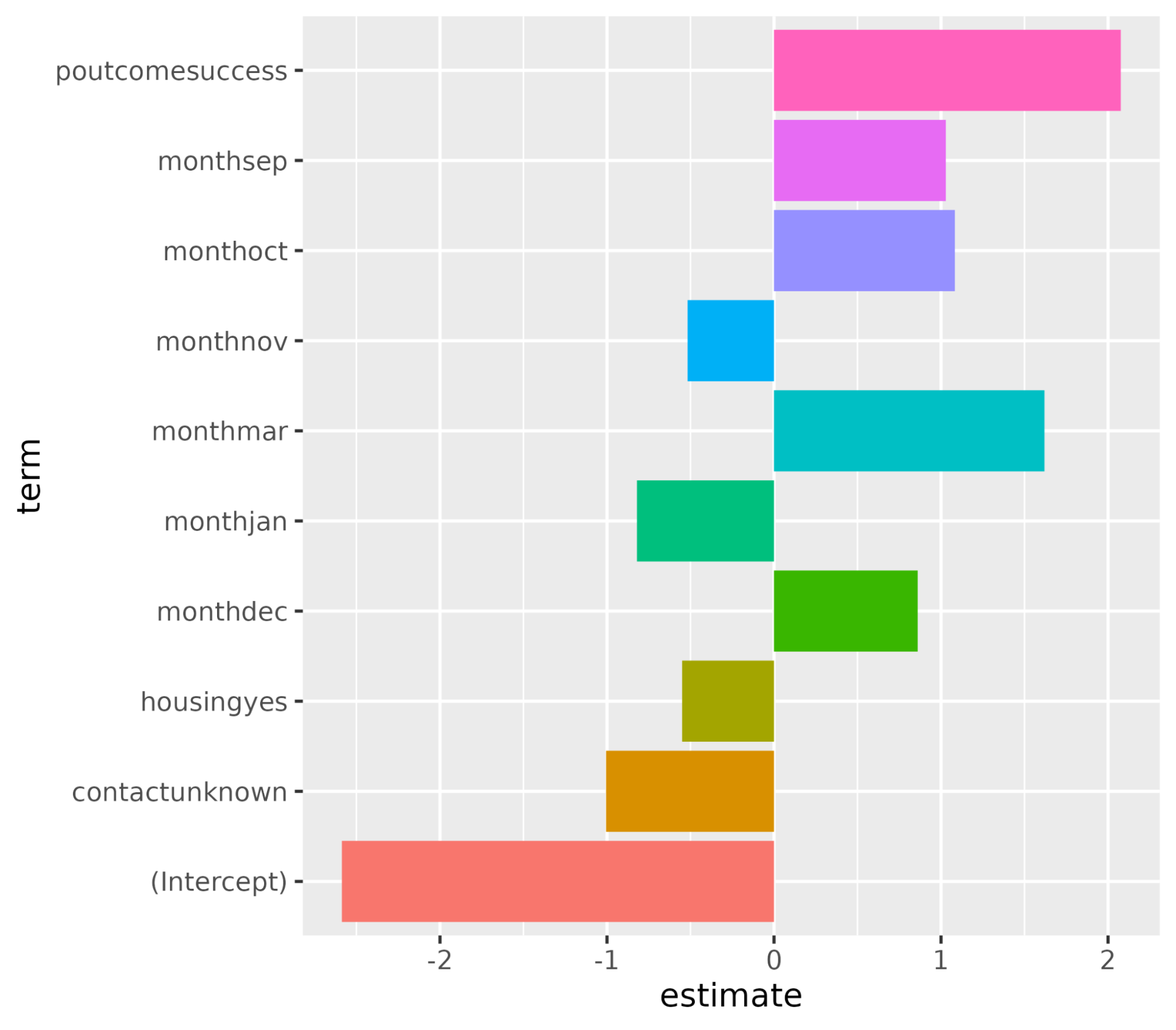

Leve-o para o próximo nível

Com isso, chegamos ao final deste tutorial que demonstrou como treinar e avaliar um modelo de regressão logística usando o pacote tidymodels. Também abordou como interpretar os resultados do modelo e plotá-los como a importância do recurso. 

Se você quiser saber mais sobre como modelar modelos de IA usando tidymodels, confira o curso Modelagem com tidymodels em R. Para modelagem usando a abordagem base-R, confira os cursos Introduction to Regression in R, Intermediate Regression in R e Generalized Linear Models in R.