Qu'est-ce que la distance de Manhattan ?

Les mesures de distance sont des outils essentiels pour mesurer la distance qui sépare des objets ou des points dans l'espace. Ces mesures jouent un rôle important dans de nombreux domaines, notamment l'apprentissage automatique, la robotique et les systèmes d'information géographique. En quantifiant les distances, nous pouvons effectuer des tâches telles que la reconnaissance des formes, le regroupement des données et l'analyse spatiale, qui sont importantes tant pour les entreprises à but lucratif que pour les chercheurs. 

La distance de Manhattan, également connue sous le nom de distance L1 ou distance taxi, est une mesure particulièrement utile pour calculer les distances dans des chemins quadrillés ou entre des points dans des espaces multidimensionnels. Nous examinerons ici à la fois les fondements mathématiques, mais aussi la manière de mettre en œuvre la distance de Manhattan à la fois en Python et en R. 

"Manhattan distance". Image par Dall-E.

N'oubliez pas que la distance de Manhattan n'est qu'une partie du sujet plus large des mesures de distance, qui apparaissent régulièrement dans toutes sortes de domaines. Pour devenir un expert de la formation à distance, pensez à notre cours Conception de workflows d'apprentissage automatique en Python ou à notre cours Analyse de clusters en R, selon votre langue de prédilection. 

Définir la distance de Manhattan

La distance de Manhattan est une mesure utilisée pour déterminer la distance entre deux points sur un chemin en forme de grille. Contrairement à la distance euclidienne, qui mesure la ligne la plus courte possible entre deux points, la distance de Manhattan mesure la somme des différences absolues entre les coordonnées des points. Cette méthode est appelée "distance de Manhattan" car, à l'instar d'un taxi circulant dans les rues quadrillées de Manhattan, il doit se déplacer le long des lignes du quadrillage. 

Mathématiquement, la distance de Manhattan entre deux points dans un espace à n dimensions est la somme des différences absolues de leurs coordonnées cartésiennes. 

La formule de la distance de Manhattan intègre la fonction de valeur absolue, qui convertit simplement les différences négatives en valeurs positives. Ce point est crucial pour le calcul de la distance, car il garantit que toutes les mesures de distance sont non négatives et reflètent la véritable distance scalaire, quelle que soit la direction du déplacement.

Calcul et visualisation de la distance de Manhattan

Comme nous l'avons dit, la distance de Manhattan est calculée en additionnant les différences absolues entre les coordonnées correspondantes de deux points. Nous allons maintenant explorer cette question à l'aide d'exemples dans l'espace 2D et 3D.

Exemple en 2D

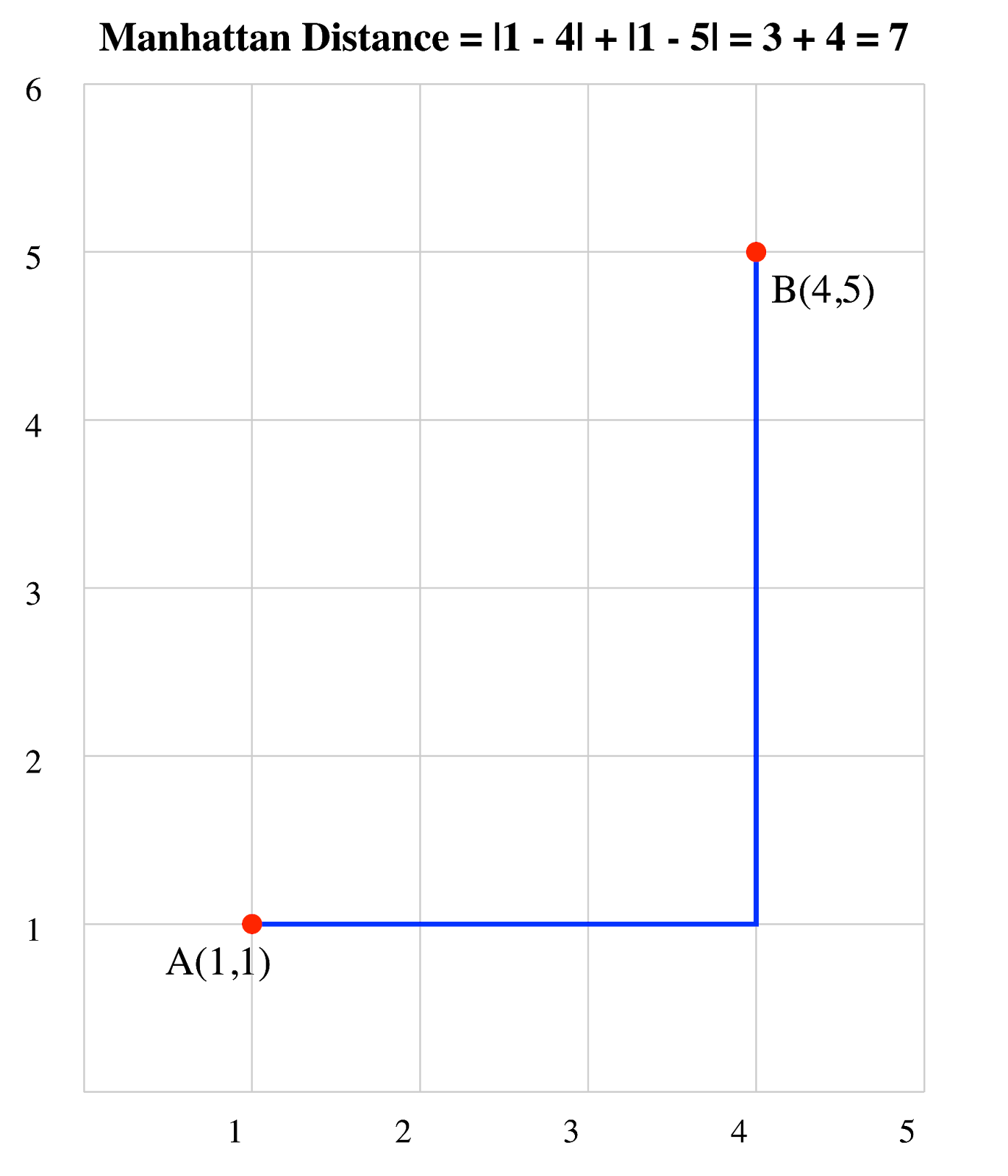
Considérez deux points : A(1, 1) et B(4, 5) :

1. Calculez |x₁ - x₂| = |1 - 4| = 3
2. Calculez |y₁ - y₂| = |1 - 5| = 4
3. Faites la synthèse des résultats : 3 + 4 = 7

Par conséquent, la distance de Manhattan entre A et B est de 7 unités. 

de deux vecteursDistance de Manhattan de deux vecteurs. Image par l'auteur.

Dans cette grille en 2D, vous pouvez voir que la distance de Manhattan suit la trajectoire qu'emprunterait un taxi, se déplaçant uniquement horizontalement et verticalement pour se rendre du point A au point B.

Exemple en 3D

Considérons maintenant deux points dans l'espace 3D : A(1, 2, 3) et B(4, 5, 6) :

1. Calculez |x₁ - x₂| = |1 - 4| = 3
2. Calculez |y₁ - y₂| = |2 - 5| = 3
3. Calculer |z₁ - z₂| = |3 - 6| = 3
4. Faites la synthèse des résultats : 3 + 3 + 3 = 9

La distance de Manhattan entre ces points 3D est de 9 unités.

Comparaison avec la distance euclidienne

Alors que la distance de Manhattan mesure la trajectoire le long des lignes de la grille, la distance euclidienne mesure la distance en ligne droite entre deux points ou, comme on dit, "à vol d'oiseau". 

Pour notre exemple en 2D :

• Distance de Manhattan : 7 unités
• Distance euclidienne : √((1-4^)² + (1-5^)²) = 5 unités

Voici une comparaison visuelle entre les distances de Manhattan et les distances euclidiennes : 

Distance de Manhattan vs. Distance euclidienne. Image par l'auteur.

Dans l'espace euclidien, la distance euclidienne est toujours inférieure ou égale à la distance de Manhattan. 

Choisir entre la distance de Manhattan et la distance euclidienne

La distance de Manhattan est particulièrement utile dans les cas suivants :

1. Les déplacements sont limités à des chemins en forme de grille (par exemple, des blocs urbains, des schémas de circuits imprimés).
2. Le déplacement en diagonale n'est pas autorisé ou est plus coûteux.
3. Vous travaillez avec des données à haute dimension dans le cadre de l'apprentissage automatique, où la distance euclidienne peut s'avérer plus efficace sur le plan informatique.
4. Vous analysez des différences dans des données discrètes ou ordinales.

En revanche, la distance euclidienne est plus appropriée dans les cas suivants :

1. Vous mesurez des distances physiques dans des espaces ouverts.
2. Vous travaillez avec des données continues où les mouvements diagonaux sont tout aussi valables.

Applications de la distance de Manhattan

La distance Manhattan trouve des applications dans divers domaines de l'informatique, de l'analyse de données et de la technologie géospatiale. Voici quelques domaines clés où la distance de Manhattan est particulièrement utile.

Algorithmes de recherche de chemin (par exemple, algorithme A*) 

Dans les environnements quadrillés, la distance de Manhattan constitue une heuristique rapide et efficace pour estimer la distance entre deux points. Il est particulièrement utile dans l'algorithme A*, où il peut aider à guider la recherche vers le but plus efficacement dans des scénarios où le mouvement est limité aux directions horizontales et verticales. Pensez aux itinéraires dans les rues des villes, aux algorithmes de résolution de labyrinthes et à certains types de cheminement de l'IA dans les jeux vidéo. 

Techniques de regroupement (par exemple, regroupement K-Means) 

La distance de Manhattan peut être utilisée comme mesure de distance dans les algorithmes de regroupement, en particulier lorsqu'il s'agit de données à haute dimension. Dans le cadre du regroupement K-Means, l'utilisation de la distance de Manhattan au lieu de la distance euclidienne peut produire de meilleurs résultats, en particulier lorsqu'il s'agit de données éparses à haute dimension ou en présence de valeurs aberrantes. En outre, il est souvent préféré pour la classification des textes et le regroupement de documents en raison de son efficacité avec les espaces vectoriels peu denses. La moindre sensibilité de la distance de Manhattan aux valeurs extrêmes dans les différentes dimensions peut conduire à des résultats de regroupement plus équilibrés dans certains ensembles de données.

Reconnaissance d'images 

La distance de Manhattan peut être utilisée pour comparer des valeurs de pixels ou des vecteurs de caractéristiques. Elle est particulièrement utile pour la recherche de modèles, lorsque vous essayez de trouver des occurrences d'une petite image dans une plus grande. Elle est également précieuse dans les systèmes de reconnaissance faciale, de détection d'objets dans les flux vidéo ou de comparaison de motifs dans les grandes bases de données d'images, où la vitesse est cruciale et où la légère perte de précision par rapport à la distance euclidienne est souvent négligeable.

Détection des valeurs aberrantes 

La distance de Manhattan peut être utilisée pour identifier les points de données qui sont significativement différents des autres dans un ensemble de données, car elle est moins sensible aux valeurs extrêmes dans les dimensions individuelles que la distance euclidienne. Cette propriété le rend utile dans les systèmes de détection d'anomalies, tels que ceux utilisés pour la détection des fraudes ou la sécurité des réseaux. Dans les systèmes financiers, par exemple, la distance de Manhattan peut aider à identifier des modèles de transaction inhabituels sans être trop influencée par les valeurs extrêmes d'un seul attribut, ce qui pourrait réduire le nombre d'erreurs.

Systèmes d'information géographique (SIG) 

Dans les applications SIG, la distance de Manhattan peut modéliser le mouvement le long d'un réseau de rues en grille, ce qui la rend utile pour la planification urbaine et la logistique. Elle est utilisée dans les problèmes d'attribution d'emplacements, tels que la détermination des emplacements optimaux pour les installations en fonction de la minimisation de la distance totale de déplacement dans une ville. La distance de Manhattan peut également être utilisée dans des tâches d'analyse spatiale, telles que la création de zones tampons autour d'éléments linéaires comme les routes ou les rivières. Les urbanistes pourraient utiliser la distance de Manhattan pour analyser l'accessibilité des services publics, tandis que les entreprises de logistique pourraient l'utiliser pour optimiser les itinéraires de livraison dans les villes.

Propriétés mathématiques de la distance de Manhattan

La distance de Manhattan possède plusieurs propriétés mathématiques importantes qui la rendent particulièrement utile. Examinons deux aspects clés : ses propriétés d'espace métrique et sa robustesse aux valeurs aberrantes.

Propriétés de l'espace métrique

La distance de Manhattan est une véritable métrique, ce qui signifie qu'elle satisfait aux quatre conditions requises pour une fonction de distance dans un espace métrique :

1. Non-négativité : La distance entre deux points quelconques est toujours non négative. d(x, y) ≥ 0 pour tout x et tout y.
2. Identité des indiscernables : La distance entre un point et lui-même est nulle, et si la distance entre deux points est nulle, il s'agit du même point. d(x, y) = 0 si et seulement si x = y.
3. Symétrie : La distance du point A au point B est la même que la distance de B à A. d(x, y) = d(y, x) pour tout x et y.
4. Inégalité des triangles : La distance entre deux points est toujours inférieure ou égale à la somme des distances entre ces points et un troisième point. d(x, z) ≤ d(x, y) + d(y, z) pour tous x, y et z.

Contrairement à la distance en cosinus, qui ne satisfait pas à l'inégalité triangulaire, la distance de Manhattan respecte toutes ces propriétés, ce qui la rend utile dans diverses applications mathématiques et informatiques. Par exemple :

• Dans les algorithmes d'optimisation, l'inégalité triangulaire peut être utilisée pour réduire efficacement les espaces de recherche.
• Dans les structures de données telles que les arbres métriques, ces propriétés permettent d'accélérer la recherche des plus proches voisins.
• Dans le domaine de l'apprentissage automatique, les algorithmes qui s'appuient sur des mesures de distance (comme les k-voisins les plus proches) peuvent tirer parti de ces propriétés pour obtenir des garanties théoriques et des mises en œuvre efficaces.

Discrimination améliorée des valeurs aberrantes 

La distance de Manhattan, avec son approche de sommation linéaire, permet souvent une meilleure discrimination des valeurs aberrantes par rapport à la distance euclidienne, qui élève les différences au carré. Cette distinction s'explique par le fait que la distance de Manhattan accumule les différences absolues dans chaque dimension de manière indépendante, réduisant ainsi l'influence écrasante des écarts importants dans une seule dimension.

Considérons deux points dans un espace 2D : A(0, 0) et B(10, 0). Introduisons maintenant un point aberrant C dont les coordonnées sont (0, 100) :

• Distance de Manhattan entre A et C : |0 - 0| + |0 - 100| = 100
• Distance euclidienne entre A et C : √((0 - 0^)² + (0 - 100^)²) = 100
• Distance de Manhattan entre B et C : |10 - 0| + |0 - 100| = 110
• Distance euclidienne entre B et C : √((10 - 0^)² + (0 - 100^)²) ≈ 100.5

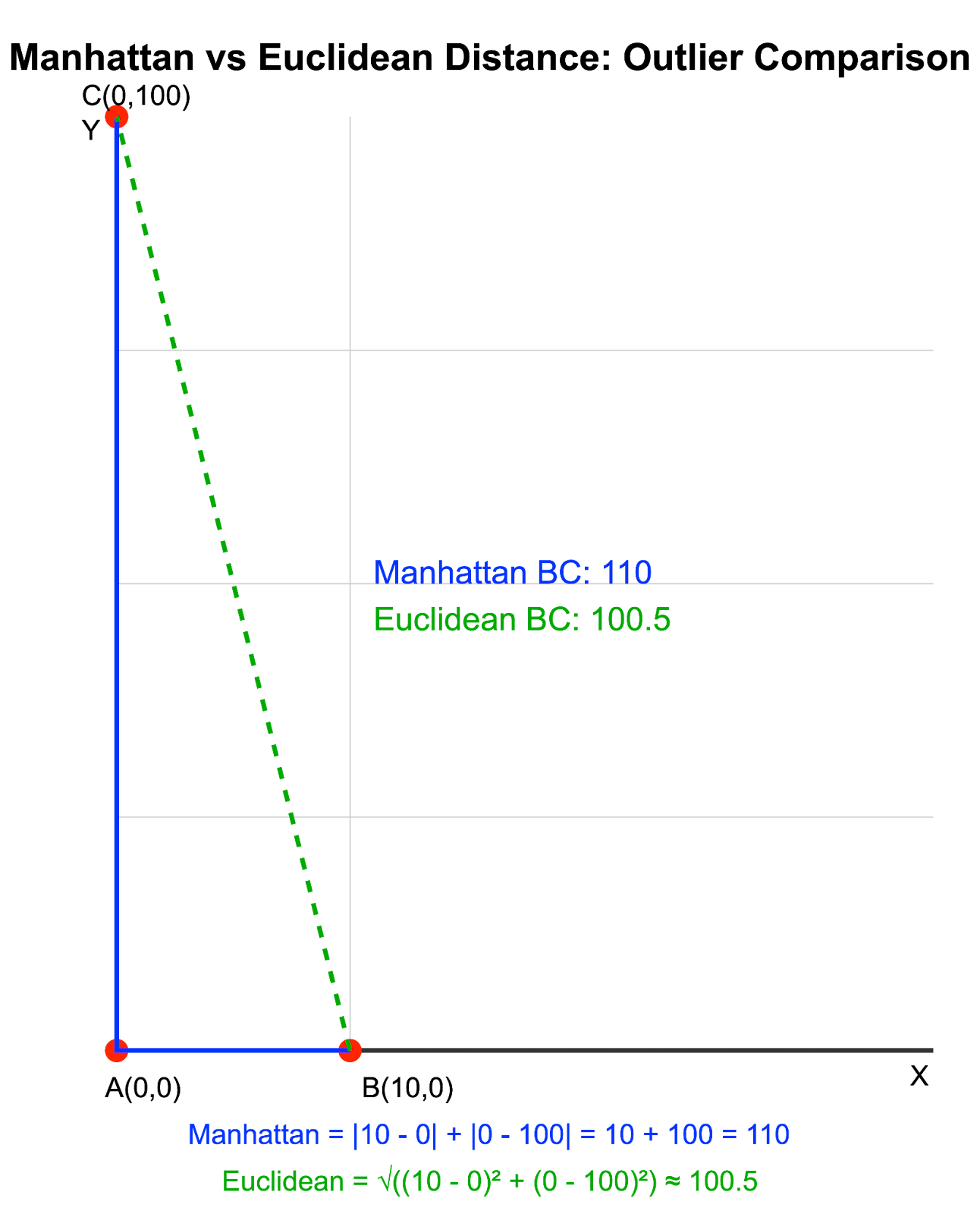Distance de Manhattan par rapport à la distance euclidienne avec des valeurs aberrantes. Image par l'auteur

Dans cet exemple, la distance de Manhattan distingue clairement les distances AC et BC, tandis que la distance euclidienne montre qu'elles sont presque identiques en raison de l'effet dominant de la valeur aberrante de la coordonnée y.

Cette propriété rend la distance de Manhattan particulièrement utile dans :

1. Espaces à haute dimension où les valeurs aberrantes sont fréquentes, comme dans le traitement d'images ou l'analyse de texte.
2. Algorithmes de clustering pour lesquels vous souhaitez réduire l'impact des valeurs aberrantes sur les centroïdes des clusters.
3. Les systèmes de détection d'anomalies dans lesquels vous souhaitez identifier les valeurs aberrantes sans en exagérer l'importance.

En étant moins sensible aux valeurs extrêmes dans les dimensions individuelles, la distance de Manhattan peut fournir une mesure plus équilibrée de la dissimilarité dans de nombreux ensembles de données du monde réel, en particulier ceux dont les données sont bruyantes ou imparfaites.

Distance de Manhattan en Python et R

Ici, nous allons explorer comment calculer la distance de Manhattan à l'aide de Python et de R. Chaque exemple démontrera différentes approches, des fonctions personnalisées aux méthodes de la bibliothèque.

Exemples en Python

Python propose plusieurs façons de calculer la distance de Manhattan. Examinons deux méthodes différentes.

1. Calcul à l'aide de tableaux NumPy :

import numpy as np
point_a_np = np.array([1, 1, 1])
point_b_np = np.array([4, 5, 6])
distance_numpy = np.sum(np.abs(point_a_np - point_b_np))
print(f"Manhattan distance (NumPy): {distance_numpy}")

Sortie : 

Manhattan distance (NumPy): 12

Cette méthode utilise directement les tableaux NumPy, ce qui peut s'avérer très efficace, en particulier lorsque vous traitez de grands ensembles de données ou que vous travaillez déjà avec des tableaux NumPy dans votre analyse.

2. Calculs effectués à l'aide de la fonction SciPy cityblock() : 

from scipy.spatial.distance import cityblock
point_a = (1, 1, 1)
point_b = (4, 5, 6)
distance_scipy = cityblock(point_a, point_b)
print(f"Manhattan distance (SciPy): {distance_scipy}")

Sortie :

Manhattan distance (SciPy): 12

SciPy fournit la fonction cityblock(), qui calcule la distance de Manhattan. Cette méthode est simple et efficace, surtout si vous travaillez avec SciPy dans votre projet. 

Exemples de R

R propose également plusieurs façons de calculer la distance de Manhattan. Examinons deux approches différentes.

1. Création d'une fonction personnalisée

manhattan_distance <- function(x1, y1, x2, y2) {
  abs(x1 - x2) + abs(y1 - y2)
}
# Example points 
point1 <- c(3, 5) # (x1, y1) 
point2 <- c(1, 9) # (x2, y2) 
# Calculate Manhattan distance between point1 and point2 
distance <- manhattan_distance(point1[1], point1[2], point2[1], point2[2]) 
print(paste("Manhattan distance (custom function):", distance))

Sortie :

"Manhattan distance (custom function): 6"

Dans cet exemple, nous créons une fonction personnalisée appelée manhattan_distance. Cette fonction prend les coordonnées de deux points comme entrées et trouve la distance de Manhattan en ajoutant les différences absolues de leurs coordonnées respectives.

2. Utilisation de la bibliothèque de statistiques

point_a <- c(1, 1, 1)
point_b <- c(4, 5, 6)
distance_builtin <- stats::dist(rbind(point_a, point_b), method = "manhattan")
print(paste("Manhattan distance:", distance_builtin))

Sortie : 

"Manhattan distance: 12"

Dans le deuxième exemple, nous utilisons la fonction dist() du paquetage stats pour calculer la distance de Manhattan. Cette approche est utile lorsqu'il s'agit de matrices ou de points multiples, car elle simplifie considérablement le processus.

Conclusion

L'importance de la distance de Manhattan réside dans sa simplicité, son efficacité informatique et sa résistance aux valeurs aberrantes dans certains scénarios. Contrairement à la distance euclidienne, la distance de Manhattan fournit souvent des résultats plus intuitifs dans les systèmes basés sur des grilles et peut être plus efficace à calculer, en particulier dans les espaces à haute dimension. 

De plus, la distance de Manhattan et d'autres mesures de distance apparaissent dans un grand nombre d'endroits. Outre notre cours Conception de workflows d'apprentissage automatique en Python, qui comporte un chapitre sur l'apprentissage basé sur la distance, et le cours Analyse de clusters en R, qui utilise des métriques basées sur la distance pour la classification et la réduction de la dimensionnalité, vous pouvez également consulter notre cours Détection d'anomalies en Python, qui utilise des métriques de distance pour la détection des valeurs aberrantes et la mise à l'échelle des caractéristiques.  

N'oubliez pas que le choix de la métrique de distance peut avoir un impact significatif sur les performances et les résultats de vos algorithmes. En comprenant quand et comment utiliser la distance de Manhattan, vous ajoutez un outil puissant à votre boîte à outils de science des données. Continuez à expérimenter, à apprendre et à repousser les limites de ce qui est possible avec les algorithmes basés sur la distance !