Introduction au k-Means Clustering avec scikit-learn en Python

Vue d'ensemble du regroupement K-Means

Les modèles de classification visent à regrouper les données en "clusters" ou groupes distincts. Cela peut constituer un point de vue intéressant dans le cadre d'une analyse ou servir de caractéristique dans un algorithme d'apprentissage supervisé. 

Prenons l'exemple d'un contexte social où des groupes de personnes discutent dans différents cercles autour d'une pièce. Lorsque vous regardez la salle pour la première fois, vous ne voyez qu'un groupe de personnes. Vous pourriez mentalement commencer à placer des points au centre de chaque groupe de personnes et nommer ce point comme identifiant unique. Vous pourrez alors vous référer à chaque groupe par un nom unique pour les décrire. C'est essentiellement ce que fait le regroupement k-means avec les données. 

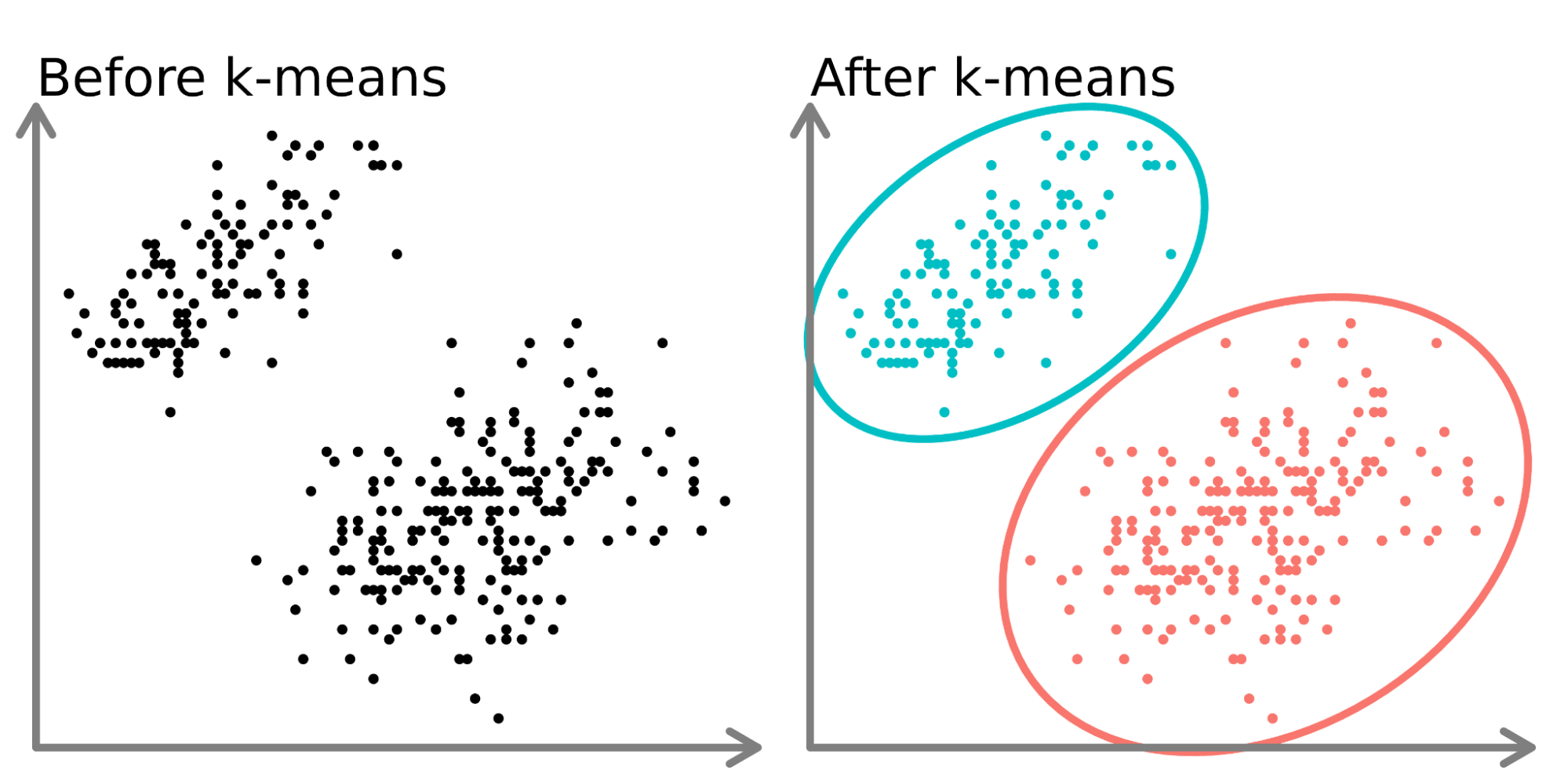
Dans la partie gauche du diagramme ci-dessus, nous pouvons voir deux ensembles distincts de points non étiquetés et colorés comme des points de données similaires. L'ajustement d'un modèle k-means à ces données (partie droite) permet de mettre en évidence deux groupes distincts (représentés par des cercles et des couleurs distincts). 

En deux dimensions, il est facile pour les humains de diviser ces groupes, mais avec plus de dimensions, vous devez utiliser un modèle.

L'ensemble de données

Dans ce tutoriel, nous utiliserons des données sur les logements en Californie provenant de Kaggle(ici). Nous utiliserons les données de localisation (latitude et longitude) ainsi que la valeur médiane des maisons. Nous regrouperons les maisons en fonction de leur emplacement et nous observerons comment les prix des maisons fluctuent en Californie. Nous enregistrons l'ensemble de données sous la forme d'un fichier csv appelé ‘housing.csv’ dans notre répertoire de travail et nous le lisons à l'aide de pandas.

import pandas as pd

home_data = pd.read_csv('housing.csv', usecols = ['longitude', 'latitude', 'median_house_value'])
home_data.head()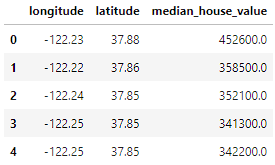

Les données comprennent 3 variables que nous avons sélectionnées à l'aide du paramètre usecols:

• longitude : Valeur représentant la distance à l'ouest d'une maison. Les valeurs les plus élevées correspondent à des maisons situées plus à l'ouest.
• latitude : Valeur représentant la distance au nord d'une maison. Les valeurs les plus élevées correspondent à des maisons situées plus au nord.
• valeur_médiane_de_la_maison : Prix médian d'un logement dans un quartier, mesuré en USD. 

Processus de clustering k-Means

Comme d'autres algorithmes d'apprentissage automatique, le k-Means Clustering a un flux de travail (voir A Beginner's Guide to The Machine Learning Workflow pour une analyse plus approfondie du flux de travail de l'apprentissage automatique).

Dans ce tutoriel, nous nous concentrerons sur la collecte et la division des données (dans la préparation des données) et l'ajustement des hyperparamètres, l'entraînement de votre modèle et l'évaluation des performances du modèle (dans la modélisation). Une grande partie du travail lié aux algorithmes d'apprentissage non supervisé réside dans le réglage des hyperparamètres et l'évaluation des performances afin d'obtenir les meilleurs résultats de votre modèle.

Visualiser les données

Nous commençons par visualiser nos données sur le logement. Nous examinons les données de localisation à l'aide d'une carte thermique basée sur le prix médian dans un pâté de maisons. Nous utiliserons Seaborn pour créer rapidement des graphiques dans ce tutoriel (consultez notre cours Introduction à la visualisation de données avec Seaborn pour mieux comprendre comment ces graphiques sont créés).

import seaborn as sns

sns.scatterplot(data = home_data, x = 'longitude', y = 'latitude', hue = 'median_house_value')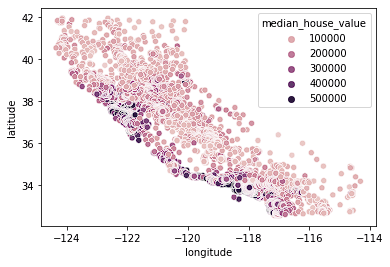

Nous constatons que la plupart des maisons chères se trouvent sur la côte ouest de la Californie, avec différentes zones où l'on trouve des groupes de maisons à prix modérés. Cette évolution est prévisible, car les propriétés situées en bord de mer valent généralement plus que les maisons qui ne sont pas situées sur la côte. 

Les grappes sont souvent faciles à repérer lorsque vous n'utilisez que 2 ou 3 caractéristiques. Elle devient de plus en plus difficile, voire impossible, lorsque le

Normaliser les données

Lorsque vous travaillez avec des algorithmes basés sur la distance, comme le regroupement k-Means, vous devez normaliser les données. Si nous ne normalisons pas les données, les variables ayant une échelle différente seront pondérées différemment dans la formule de distance optimisée pendant la formation. Par exemple, si nous devions inclure le prix dans le groupe, en plus de la latitude et de la longitude, le prix aurait un impact considérable sur les optimisations, car son échelle est beaucoup plus grande et plus large que les variables de localisation délimitées. 

Nous avons d'abord établi des divisions d'entraînement et de test en utilisant train_test_split à partir de sklearn. 

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(home_data[['latitude', 'longitude']], home_data[['median_house_value']], test_size=0.33, random_state=0)

Ensuite, nous normalisons les données de formation et de test à l'aide de la méthode preprocessing.normalize() de sklearn. 

from sklearn import preprocessing

X_train_norm = preprocessing.normalize(X_train)
X_test_norm = preprocessing.normalize(X_test)

Ajustement et évaluation du modèle

Pour la première itération, nous choisirons arbitrairement un nombre de grappes (appelé k) de 3. La construction et l'ajustement de modèles dans sklearn sont très simples. Nous allons créer une instance de KMeans, définir le nombre de grappes à l'aide de l'attribut n_clusters, fixer n_init, qui définit le nombre d'itérations que l'algorithme exécutera avec différentes graines de centroïdes, à "auto", et fixer random_state à 0 afin d'obtenir le même résultat à chaque fois que nous exécutons le code.  Nous pouvons ensuite adapter le modèle aux données d'apprentissage normalisées à l'aide de la méthode fit().

from sklearn import KMeans

kmeans = KMeans(n_clusters = 3, random_state = 0, n_init='auto')
kmeans.fit(X_train_norm)

Une fois les données ajustées, nous pouvons accéder aux étiquettes à partir de l'attribut labels_. Ci-dessous, nous visualisons les données que nous venons d'ajuster. 

sns.scatterplot(data = X_train, x = 'longitude', y = 'latitude', hue = kmeans.labels_)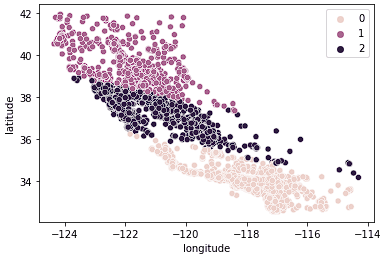

Nous constatons que les données sont maintenant clairement réparties en trois groupes distincts (Californie du Nord, Californie centrale et Californie du Sud). Nous pouvons également examiner la distribution des prix médians des logements dans ces trois groupes à l'aide d'un diagramme en boîte. 

sns.boxplot(x = kmeans.labels_, y = y_train['median_house_value'])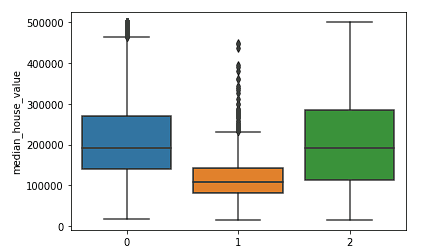

Nous voyons clairement que les groupes nord et sud ont des distributions similaires de valeurs médianes des maisons (groupes 0 et 2) qui sont plus élevées que les prix dans le groupe central (groupe 1). 

Nous pouvons évaluer les performances de l'algorithme de regroupement à l'aide d'un score de Silhouette qui est une partie de sklearn.metrics où un score plus faible représente une meilleure adéquation.

from sklearn.metrics import silhouette_score

silhouette_score(X_train_norm, kmeans.labels_, metric='euclidean')

Comme nous n'avons pas examiné la force des différents nombres de grappes, nous ne savons pas dans quelle mesure le modèle k = 3 est adapté. Dans la section suivante, nous explorerons différents groupes et comparerons les performances afin de prendre une décision sur les meilleures valeurs d'hyperparamètres pour notre modèle.

Choisir le meilleur nombre de grappes

La faiblesse du regroupement par k-means est que nous ne savons pas combien de grappes nous avons besoin en exécutant simplement le modèle. Nous devons tester des fourchettes de valeurs et prendre une décision sur la meilleure valeur de k. Nous prenons généralement une décision à l'aide de la méthode du coude pour déterminer le nombre optimal de grappes afin de ne pas suradapter les données avec un trop grand nombre de grappes et de ne pas les sous-adapter avec un trop petit nombre de grappes. 

Nous créons la boucle ci-dessous pour tester et stocker les différents résultats du modèle afin de prendre une décision sur le meilleur nombre de grappes.

K = range(2, 8)
fits = []
score = []


for k in K:
    # train the model for current value of k on training data
    model = KMeans(n_clusters = k, random_state = 0, n_init='auto').fit(X_train_norm)
    
    # append the model to fits
    fits.append(model)
    
    # Append the silhouette score to scores
    score.append(silhouette_score(X_train_norm, model.labels_, metric='euclidean'))

Nous pouvons donc commencer par examiner visuellement quelques valeurs différentes de k. 

Examinons d'abord k = 2.

sns.scatterplot(data = X_train, x = 'longitude', y = 'latitude', hue = fits[0].labels_)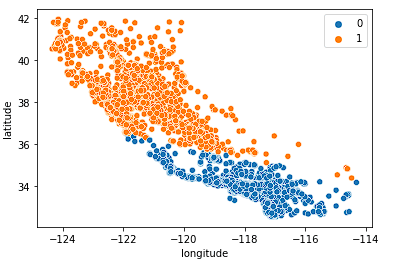

Le modèle divise bien l'État en deux moitiés, mais ne saisit probablement pas assez de nuances dans le marché immobilier californien. 

Nous examinons ensuite le cas de k = 4. 

sns.scatterplot(data = X_train, x = 'longitude', y = 'latitude', hue = fits[2].labels_)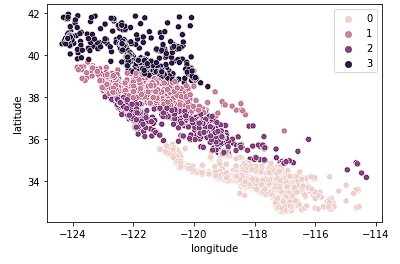

Nous voyons que ce graphique regroupe la Californie en groupes plus logiques à travers l'État en fonction de la distance au nord ou au sud des maisons dans l'État. Ce modèle permet très probablement de saisir davantage de nuances dans le marché du logement à mesure que l'on se déplace dans l'État. 

Enfin, nous examinons k = 7.

sns.scatterplot(data = X_train, x = 'longitude', y = 'latitude', hue = fits[2].labels_)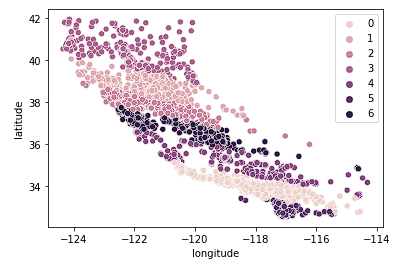

Le graphique ci-dessus semble comporter trop de grappes. Nous avons sacrifié la facilité d'interprétation des clusters pour un résultat de géo-clustering "plus précis". 

En règle générale, lorsque nous augmentons la valeur de K, nous constatons des améliorations dans les grappes et ce qu'elles représentent jusqu'à un certain point. Nous commençons alors à observer des rendements décroissants, voire une détérioration des performances. Nous pouvons visualiser cela pour nous aider à prendre une décision sur la valeur de k en utilisant un graphique en coude où l'axe des y est une mesure de la qualité de l'ajustement et l'axe des x est la valeur de k. 

sns.lineplot(x = K, y = score)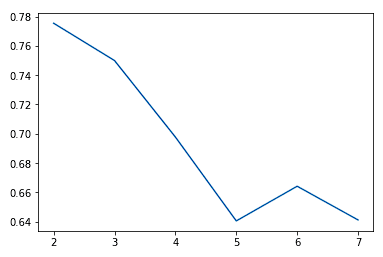

Nous choisissons généralement le point où l'amélioration des performances commence à s'estomper ou à s'aggraver. Nous constatons que k = 5 est probablement le meilleur résultat que nous puissions obtenir sans surajustement. 

Nous pouvons également constater que les grappes permettent relativement bien de diviser la Californie en groupes distincts et que ces groupes correspondent relativement bien aux différentes fourchettes de prix, comme le montre le tableau ci-dessous. 

sns.scatterplot(data = X_train, x = 'longitude', y = 'latitude', hue = fits[3].labels_)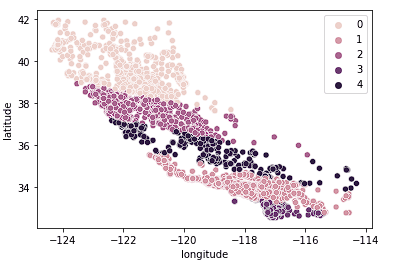

sns.boxplot(x = fits[3].labels_, y = y_train['median_house_value'])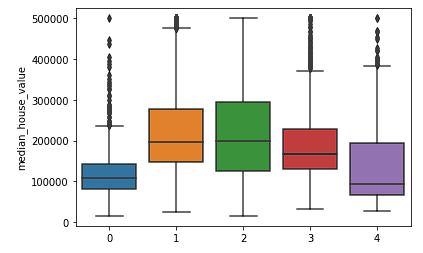

Quand l'analyse en grappes k-means échoue-t-elle ?

Le regroupement K-means est le plus performant pour les données sphériques. Les données sphériques sont des données qui se regroupent dans l'espace à proximité les unes des autres. Cela peut être visualisé plus facilement dans un espace à 2 ou 3 dimensions. Les données qui ne sont pas sphériques ou qui ne devraient pas l'être ne fonctionnent pas bien avec le regroupement k-means. Par exemple, le regroupement par k-moyennes ne donnerait pas de bons résultats sur les données ci-dessous, car nous ne pourrions pas trouver de centroïdes distincts pour regrouper différemment les deux cercles ou arcs, bien qu'ils soient visuellement deux cercles et arcs distincts qui devraient être étiquetés en tant que tels. 

Image Source 

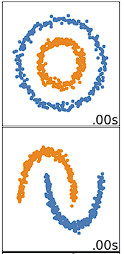
Il existe de nombreux autres algorithmes de regroupement qui permettent de regrouper efficacement des données non sphériques. Ces algorithmes sont décrits dans le site Clustering in Machine Learning (regroupement dans l'apprentissage automatique) : 5 Algorithmes de regroupement essentiels.

Devriez-vous diviser vos données en ensembles de formation et de test ?

La décision de diviser vos données dépend de vos objectifs en matière de regroupement. Si l'objectif est de regrouper vos données à la fin de votre analyse, ce n'est pas nécessaire. Si vous utilisez les grappes comme caractéristique dans un modèle d'apprentissage supervisé ou pour la prédiction (comme nous le faisons dans le didacticiel Scikit-Learn à l'adresse ) : Baseball Analytics Pt 1 tutorial), vous devrez diviser vos données avant de les regrouper afin de vous assurer que vous suivez les meilleures pratiques pour le flux de travail de l'apprentissage supervisé. 

Passez au niveau supérieur

Maintenant que nous avons couvert les bases du clustering k-means en Python, vous pouvez consulter ce cours sur l 'apprentissage non supervisé en Python pour une bonne introduction aux k-means et à d'autres algorithmes d'apprentissage non supervisé. Notre cours plus avancé, Cluster Analysis in Python, donne un aperçu plus approfondi des algorithmes de clustering et de la façon de les construire et de les régler en Python. Enfin, vous pouvez également consulter le tutoriel Une introduction au clustering hiérarchique en Python comme une approche qui utilise un algorithme alternatif pour créer des hiérarchies à partir de données.