O que é a distância de Manhattan?

"Manhattan distance" (Distância de Manhattan). Imagem de Dall-E.

As métricas de distância são ferramentas essenciais para medir a distância entre objetos ou pontos no espaço. Essas métricas desempenham um papel importante em muitos campos, incluindo machine learning, robótica e sistemas de informações geográficas. Ao quantificar as distâncias, podemos executar tarefas como reconhecimento de padrões, agrupamento de dados e análise espacial, que são importantes tanto para empresas com fins lucrativos quanto para pesquisadores. 

A distância de Manhattan, também conhecida como distância L1 ou distância de táxi, destaca-se como uma medida particularmente útil para calcular distâncias em caminhos semelhantes a grades ou entre pontos em espaços multidimensionais. Aqui, veremos a base matemática e também como implementar a distância de Manhattan no Python e no R. Você pode usar a distância de Manhattan para fazer isso. 

Lembre-se de que a distância de Manhattan é apenas uma parte do tópico mais amplo de métricas de distância, que aparecem repetidamente em todos os tipos de campos. Para se tornar um especialista em ensino à distância, considere nosso curso Designing Machine Learning Workflows in Python ou nosso curso Cluster Analysis in R, dependendo do idioma que você preferir. 

Definição da distância de Manhattan

A distância de Manhattan é uma métrica usada para determinar a distância entre dois pontos em um caminho semelhante a uma grade. Diferentemente da distância euclidiana, que mede a linha mais curta possível entre dois pontos, a distância de Manhattan mede a soma das diferenças absolutas entre as coordenadas dos pontos. Esse método é chamado de "distância de Manhattan" porque, como um táxi dirigindo pelas ruas em forma de grade de Manhattan, ele deve viajar ao longo das linhas da grade. 

Matematicamente, a distância de Manhattan entre dois pontos em um espaço n-dimensional é a soma das diferenças absolutas de suas coordenadas cartesianas. 

A fórmula da distância de Manhattan incorpora a função de valor absoluto, que simplesmente converte quaisquer diferenças negativas em valores positivos. Isso é fundamental para o cálculo da distância, pois garante que todas as medições de distância sejam não negativas, refletindo a verdadeira distância escalar, independentemente da direção da viagem.

Cálculo e visualização da distância de Manhattan

Como já dissemos, a distância de Manhattan é calculada pela soma das diferenças absolutas entre as coordenadas correspondentes de dois pontos. Vamos agora explorar isso com exemplos no espaço 2D e 3D.

Exemplo 2D

Considere dois pontos: A(1, 1) e B(4, 5):

1. Calculate |x₁ - x₂| = |1 - 4| = 3
2. Calculate |y₁ - y₂| = |1 - 5| = 4
3. Some os resultados: 3 + 4 = 7

Portanto, a distância de Manhattan entre A e B é de 7 unidades. 

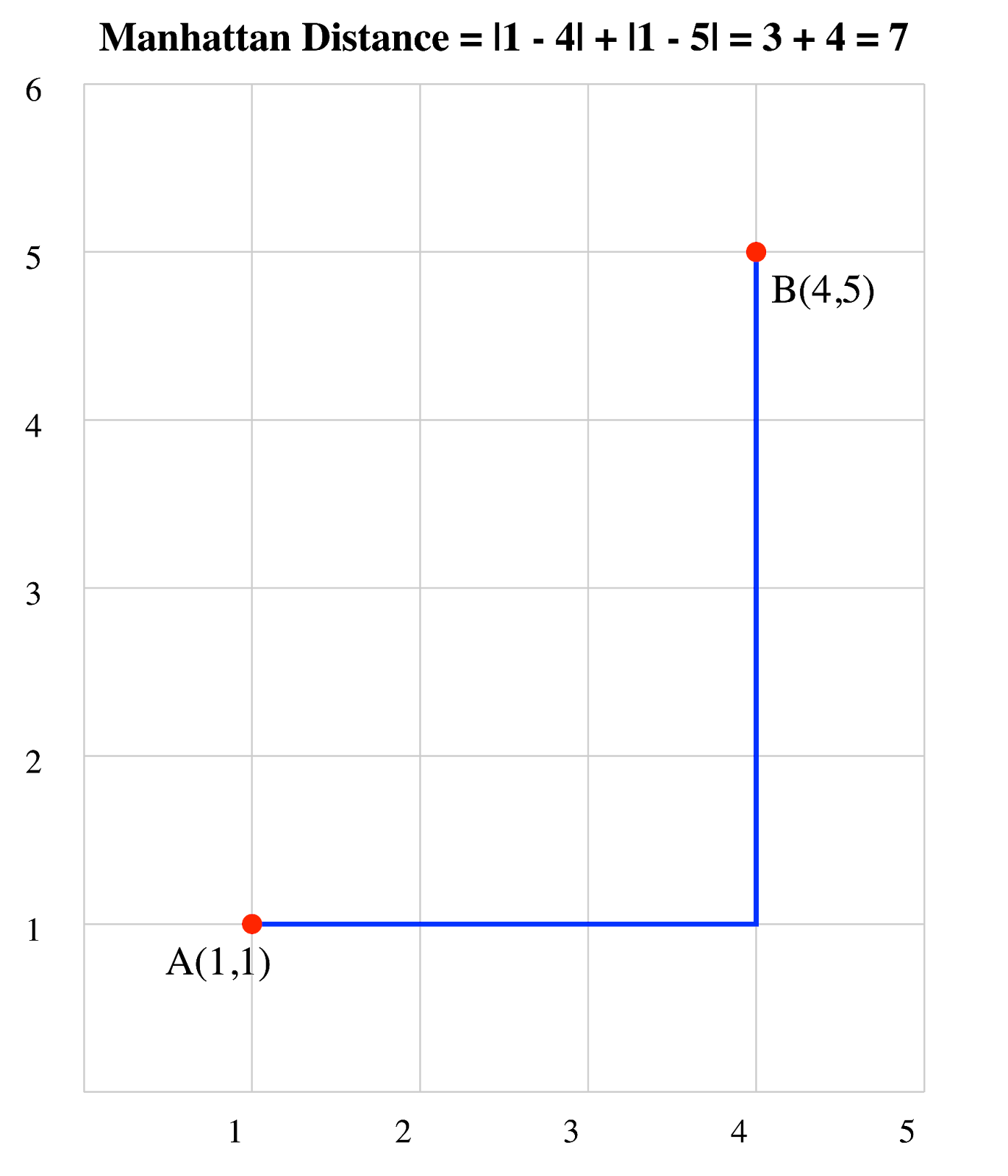Distância de Manhattan de dois vetores. Imagem do autor.

Nessa grade 2D, você pode ver que a distância de Manhattan segue o caminho que um táxi tomaria, movendo-se apenas horizontal e verticalmente para ir do ponto A ao ponto B.

Exemplo em 3D

Agora, vamos considerar dois pontos no espaço 3D: A(1, 2, 3) e B(4, 5, 6):

1. Calculate |x₁ - x₂| = |1 - 4| = 3
2. Calculate |y₁ - y₂| = |2 - 5| = 3
3. Calcule |z₁ - z₂| = |3 - 6| = 3
4. Some os resultados: 3 + 3 + 3 = 9

A distância de Manhattan entre esses pontos 3D é de 9 unidades.

Comparação com a distância euclidiana

Enquanto a distância de Manhattan mede o caminho ao longo das linhas de grade, a distância euclidiana mede a distância em linha reta entre dois pontos ou, "como o corvo voa", como dizem. 

Para o nosso exemplo 2D:

• Distância de Manhattan: 7 unidades
• Distância euclidiana: √((1-4^)² + (1-5^)²) = 5 unidades

Aqui está uma comparação visual entre as distâncias de Manhattan e euclidiana: 

Distância de Manhattan vs. distância . Distância euclidiana. Imagem do autor.

No espaço euclidiano, a distância euclidiana é sempre menor ou igual à distância de Manhattan. 

Escolhendo entre a distância de Manhattan e a distância euclidiana

A distância de Manhattan é particularmente útil em cenários em que:

1. O movimento é restrito a caminhos semelhantes a grades (por exemplo, quarteirões de cidades, layouts de placas de circuito).
2. O movimento diagonal não é permitido ou é mais caro.
3. Você está trabalhando com dados de alta dimensão em machine learning, onde pode ser computacionalmente mais eficiente do que a distância euclidiana.
4. Você está analisando diferenças em dados discretos ou ordinais.

Por outro lado, a distância euclidiana é mais apropriada quando você tem que se preocupar com a distância euclidiana:

1. Você está medindo distâncias físicas em espaços abertos.
2. Você está trabalhando com dados contínuos em que os movimentos diagonais são igualmente válidos.

Aplicações da distância de Manhattan

A distância de Manhattan encontra aplicações em vários campos da ciência da computação, análise de dados e tecnologia geoespacial. Aqui estão algumas áreas importantes em que a distância de Manhattan é particularmente útil.

Algoritmos de localização de caminhos (por exemplo, algoritmo A*) 

Em ambientes baseados em grade, a distância Manhattan oferece uma heurística rápida e eficaz para estimar a distância entre dois pontos. Ele é particularmente útil no algoritmo A*, onde pode ajudar a orientar a busca em direção à meta de forma mais eficiente em cenários em que o movimento é restrito às direções horizontal e vertical. Pense no roteamento nas ruas da cidade, nos algoritmos de solução de labirintos e em certos tipos de localização de caminhos de IA de videogames. 

Técnicas de agrupamento (por exemplo, agrupamento K-Means) 

A distância de Manhattan pode ser usada como uma métrica de distância em algoritmos de agrupamento, especialmente ao lidar com dados de alta dimensão. No agrupamento K-Means, o uso da distância de Manhattan em vez da distância euclidiana pode produzir melhores resultados, especialmente quando você lida com dados esparsos de alta dimensão ou quando há outliers. Além disso, ele costuma ser preferido na classificação de textos e no agrupamento de documentos devido à sua eficácia com espaços vetoriais esparsos. A menor sensibilidade da distância de Manhattan a valores extremos em dimensões individuais pode levar a resultados de agrupamento mais equilibrados em determinados conjuntos de dados.

Reconhecimento de imagens 

A distância de Manhattan pode ser usada para comparar valores de pixel ou vetores de recursos. É particularmente útil na correspondência de modelos, em que você está tentando encontrar ocorrências de uma imagem pequena em uma imagem maior. Ela também é valiosa em sistemas de reconhecimento facial, detecção de objetos em fluxos de vídeo ou correspondência de padrões em grandes bancos de dados de imagens, em que a velocidade é crucial, e a pequena perda de precisão em comparação com a distância euclidiana costuma ser insignificante.

Detecção de outlier 

A distância de Manhattan pode ser usada para identificar pontos de dados que são significativamente diferentes de outros em um conjunto de dados porque é menos sensível a valores extremos em dimensões individuais em comparação com a distância euclidiana. Essa propriedade o torna útil em sistemas de detecção de anomalias, como os usados em detecção de fraudes ou segurança de rede. Nos sistemas financeiros, por exemplo, a distância de Manhattan pode ajudar a identificar padrões de transações incomuns sem ser excessivamente influenciada por valores extremos em um único atributo, o que pode levar a menos erros.

Sistemas de informações geográficas (GIS) 

Em aplicativos GIS, a distância de Manhattan pode modelar o movimento ao longo de uma rede de ruas em forma de grade, tornando-a útil para o planejamento urbano e a logística. É usado em problemas de alocação de locais, como a determinação de locais ideais para instalações com base na minimização da distância total de deslocamento em uma cidade. A distância de Manhattan também pode ser aplicada em tarefas de análise espacial, como a criação de zonas de proteção em torno de recursos lineares, como estradas ou rios. Os planejadores urbanos podem usar a distância de Manhattan para analisar a acessibilidade dos serviços públicos, enquanto as empresas de logística podem empregá-la para otimizar as rotas de entrega nas cidades.

Propriedades matemáticas da distância de Manhattan

A distância de Manhattan possui várias propriedades matemáticas importantes que a tornam particularmente útil. Vamos explorar dois aspectos principais: suas propriedades de espaço métrico e sua robustez em relação a outliers.

Propriedades do espaço métrico

A distância de Manhattan é uma verdadeira métrica, o que significa que ela satisfaz todas as quatro condições necessárias para uma função de distância em um espaço métrico:

1. Não negatividade: A distância entre dois pontos quaisquer é sempre não negativa. d(x, y) ≥ 0 para todos os x e y.
2. Identidade de indiscerníveis: A distância entre um ponto e ele mesmo é zero, e se a distância entre dois pontos for zero, eles são o mesmo ponto. d(x, y) = 0 se e somente se x = y.
3. Simetria: A distância do ponto A ao ponto B é a mesma que a distância de B a A. d(x, y) = d(y, x) para todos os x e y.
4. Desigualdade triangular: A distância entre dois pontos é sempre menor ou igual à soma das distâncias entre esses pontos e um terceiro ponto. d(x, z) ≤ d(x, y) + d(y, z) para todos os x, y e z.

Diferentemente da distância de cosseno, que não satisfaz a desigualdade triangular, a adesão da distância de Manhattan a todas essas propriedades a torna útil em várias aplicações matemáticas e computacionais. Por exemplo:

• Em algoritmos de otimização, a desigualdade triangular pode ser usada para eliminar espaços de pesquisa com eficiência.
• Em estruturas de dados como árvores métricas, essas propriedades permitem pesquisas mais rápidas do vizinho mais próximo.
• No machine learning, os algoritmos que se baseiam em métricas de distância (como k-nearest neighbors) podem aproveitar essas propriedades para obter garantias teóricas e implementações eficientes.

Discriminação aprimorada de outlier 

A distância de Manhattan, com sua abordagem de soma linear, geralmente oferece uma discriminação aprimorada de outliers em comparação com a distância euclidiana, que eleva as diferenças ao quadrado. Essa distinção ocorre porque a distância de Manhattan acumula as diferenças absolutas em cada dimensão de forma independente, reduzindo a influência esmagadora de grandes discrepâncias em uma única dimensão.

Considere dois pontos em um espaço 2D: A(0, 0) e B(10, 0). Agora, vamos introduzir um ponto de exceção C com coordenadas (0, 100):

• Distância de Manhattan entre A e C: |0 - 0| + |0 - 100| = 100
• Distância euclidiana entre A e C: √((0 - 0^)² + (0 - 100^)²) = 100
• Distância de Manhattan entre B e C: |10 - 0| + |0 - 100| = 110
• Distância euclidiana entre B e C: √((10 - 0^)² + (0 - 100^)²) ≈ 100,5

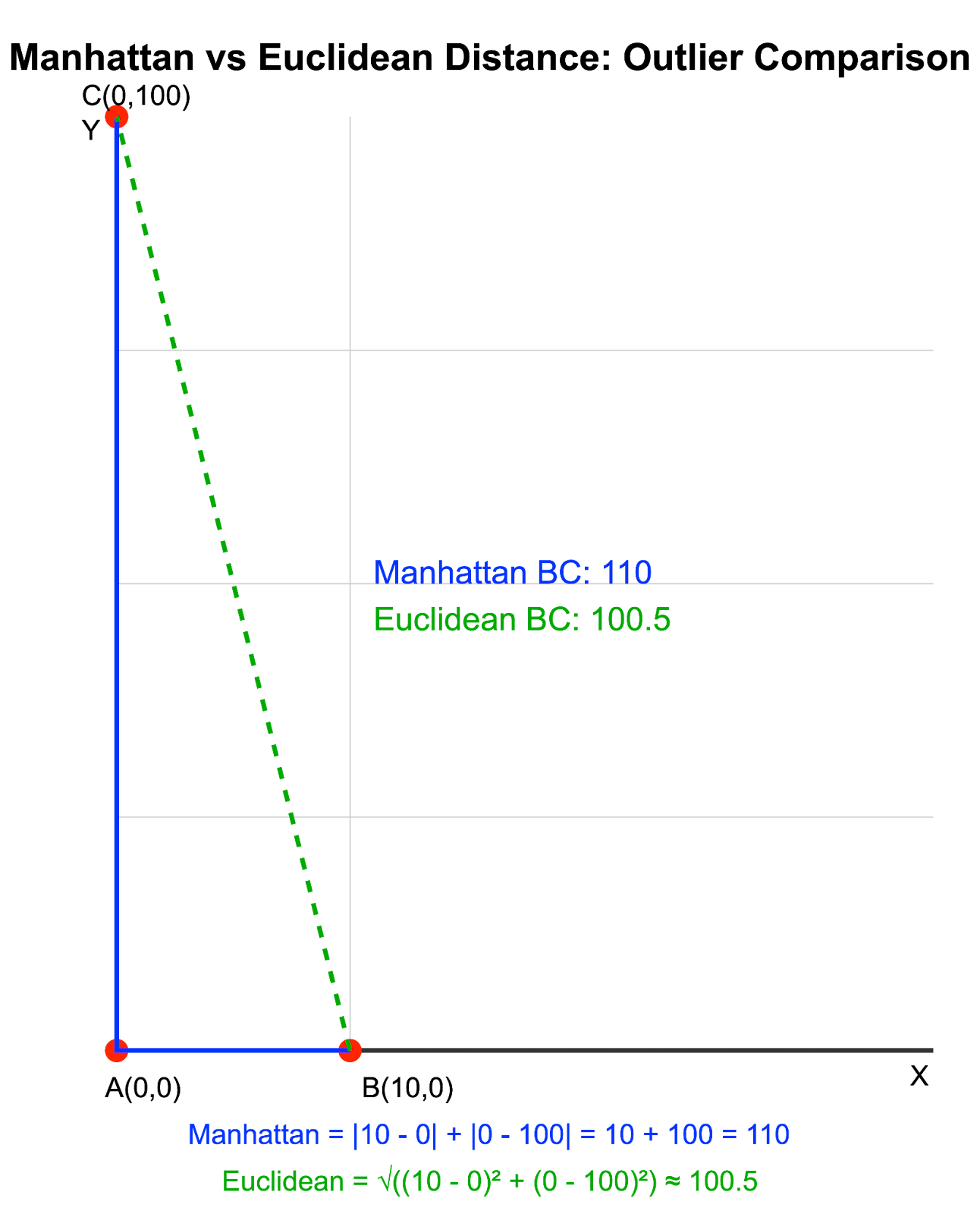Distância Manhattan vs. Euclidiana com outliers. Imagem do autor

Neste exemplo, a distância de Manhattan distingue claramente entre as distâncias AC e BC, enquanto a distância euclidiana as mostra quase iguais devido ao efeito dominante do outlier na coordenada y.

Essa propriedade torna a distância de Manhattan particularmente útil para você:

1. Espaços de alta dimensão em que os valores discrepantes são comuns, como no processamento de imagens ou na análise de texto.
2. Algoritmos de agrupamento em que você deseja reduzir o impacto de outliers nos centroides de agrupamento.
3. Sistemas de detecção de anomalias em que você deseja identificar discrepâncias sem aumentar excessivamente sua importância.

Por ser menos sensível a valores extremos em dimensões individuais, a distância Manhattan pode fornecer uma medida mais equilibrada de dissimilaridade em muitos conjuntos de dados do mundo real, especialmente aqueles com dados ruidosos ou imperfeitos.

Distância de Manhattan em Python e R

Aqui, exploraremos como calcular a distância de Manhattan usando Python e R. Cada exemplo demonstrará diferentes abordagens, desde funções personalizadas até métodos de biblioteca.

Exemplos em Python

O Python oferece várias maneiras de calcular a distância de Manhattan. Vamos explorar dois métodos diferentes.

1. Cálculo usando matrizes NumPy:

import numpy as np
point_a_np = np.array([1, 1, 1])
point_b_np = np.array([4, 5, 6])
distance_numpy = np.sum(np.abs(point_a_np - point_b_np))
print(f"Manhattan distance (NumPy): {distance_numpy}")

Saída: 

Manhattan distance (NumPy): 12

Esse método usa diretamente matrizes NumPy, o que pode ser muito eficiente, especialmente ao lidar com grandes conjuntos de dados ou quando você já estiver trabalhando com matrizes NumPy em sua análise.

2. Cálculo usando a função cityblock() do SciPy: 

from scipy.spatial.distance import cityblock
point_a = (1, 1, 1)
point_b = (4, 5, 6)
distance_scipy = cityblock(point_a, point_b)
print(f"Manhattan distance (SciPy): {distance_scipy}")

Saída:

Manhattan distance (SciPy): 12

O SciPy fornece a função cityblock(), que calcula a distância de Manhattan. Esse método é simples e eficiente, especialmente quando você trabalha com SciPy em seu projeto. 

Exemplos de R

O R também oferece várias maneiras de calcular a distância de Manhattan. Vamos examinar duas abordagens diferentes.

1. Criando uma função personalizada

manhattan_distance <- function(x1, y1, x2, y2) {
  abs(x1 - x2) + abs(y1 - y2)
}
# Example points 
point1 <- c(3, 5) # (x1, y1) 
point2 <- c(1, 9) # (x2, y2) 
# Calculate Manhattan distance between point1 and point2 
distance <- manhattan_distance(point1[1], point1[2], point2[1], point2[2]) 
print(paste("Manhattan distance (custom function):", distance))

Saída:

"Manhattan distance (custom function): 6"

Neste exemplo, criamos uma função personalizada chamada manhattan_distance. Essa função usa as coordenadas de dois pontos como entradas e encontra a distância de Manhattan adicionando as diferenças absolutas de suas respectivas coordenadas.

2. Usando a biblioteca de estatísticas

point_a <- c(1, 1, 1)
point_b <- c(4, 5, 6)
distance_builtin <- stats::dist(rbind(point_a, point_b), method = "manhattan")
print(paste("Manhattan distance:", distance_builtin))

Saída: 

"Manhattan distance: 12"

No segundo exemplo, utilizamos a função dist() do pacote stats para calcular a distância de Manhattan. Essa abordagem é útil ao lidar com matrizes ou vários pontos, pois simplifica significativamente o processo.

Conclusão

A importância da distância de Manhattan está em sua simplicidade, eficiência computacional e robustez em relação a outliers em determinados cenários. Ao contrário da distância euclidiana, a distância de Manhattan geralmente fornece resultados mais intuitivos em sistemas baseados em grade e pode ser mais eficiente para o cálculo, especialmente em espaços de alta dimensão. 

Além disso, a distância de Manhattan e outras métricas de distância aparecem em uma grande variedade de lugares. Além do nosso curso Designing Machine Learning Workflows in Python, que apresenta um capítulo sobre aprendizado baseado em distância, e do curso Cluster Analysis in R, que usa métricas baseadas em distância para classificação e redução de dimensionalidade, você também pode conferir nosso curso Anomaly Detection in Python, que usa métricas de distância para detecção de outlier e dimensionamento de recursos.  

Lembre-se de que a escolha da métrica de distância pode afetar significativamente o desempenho e os resultados de seus algoritmos. Ao entender quando e como usar a distância de Manhattan, você estará adicionando uma ferramenta poderosa ao seu kit de ferramentas de ciência de dados. Continue experimentando, aprendendo e ampliando os limites do que é possível fazer com algoritmos baseados em distância!