Implémentation de l'algorithme Minimax pour l'IA en Python

L'algorithme Mini-Max a une riche histoire dans le domaine de l'IA, qui remonte aux années 1920. Bien que le terme "IA" n'ait pas été utilisé pour désigner les algorithmes informatiques à l'époque, l'algorithme fondateur a certainement donné certaines des premières indications sur la manière dont les machines pouvaient prendre des décisions optimales dans des scénarios contradictoires. L'algorithme a été formalisé pour la première fois par John von Neumann dans son article de 1928 intitulé "Zur Theorie der Gesellschaftsspiele" (Sur la théorie des jeux de stratégie), qui a jeté les bases de la théorie moderne des jeux et des algorithmes de prise de décision.

En 1997, Deep Blue d'IBM a battu le champion du monde d'échecs Garry Kasparov en utilisant les variantes avancées de Mini-max. Depuis lors, l'algorithme a servi de base à des approches plus sophistiquées telles que la recherche arborescente de Monte Carlo (MCTS) et l l'apprentissage par renforcement d'apprentissage par renforcement.

Dans cet article, nous ne reconstruirons pas le célèbre Deep Blue pour les échecs mais une version bien plus simple pour le morpion en Python. En cours de route, vous acquerrez une forte intuition sur le fonctionnement de l'algorithme et sur la manière de l'appliquer à des jeux réels plus complexes.

Qu'est-ce que l'algorithme Minimax ?

Minimax est généralement un algorithme de prise de décision pour les jeux à deux joueurs (comme les échecs, le morpion ou les dames). Il permet aux ordinateurs de planifier plusieurs mouvements tout en supposant que votre adversaire fera toujours le meilleur mouvement possible. Dans cette section, nous allons donner un aperçu de l'algorithme à travers l'exemple du morpion.

Aperçu de l'algorithme Minimax

Dans un morpion du monde réel, à chaque fois que c'est votre tour, vous essayez de faire le meilleur mouvement possible tout en supposant que votre adversaire jouera également de son mieux. C'est exactement ce que fait l'algorithme Minimax : il aide l'ordinateur à effectuer le meilleur mouvement possible en réfléchissant à l'avance à tous les mouvements possibles.

L'algorithme Minimax tire son nom de son fonctionnement :

• "Mini" représente l'adversaire qui tente de minimiser votre score.
• "Max" représente le fait que vous essayez de maximiser votre score.

Lorsque c'est votre tour, vous voulez jouer les coups qui vous donnent les meilleures chances de gagner (maximisation). Lorsque c'est au tour de votre adversaire, vous supposez qu'il jouera les coups qui vous donneront le pire résultat (minimiser).

L'importance de Minimax dans l'IA

La méthode Minimax est très importante en intelligence artificielle pour plusieurs raisons :

1. Il aide les ordinateurs à prendre des décisions intelligentes dans les jeux à deux joueurs.
2. C'est le fondement de nombreux systèmes modernes d'intelligence artificielle pour le jeu.
3. Il apprend aux ordinateurs à penser à l'avance et à planifier les déplacements.

Le plus intéressant ? Cette même idée est utilisée dans de nombreuses applications du monde réel :

• Adversaires de l'IA dans les jeux vidéo
• Jeux de stratégie comme les échecs et les dames
• Même certains outils d'aide à la décision pour les entreprises

Le Minimax peut sembler compliqué, mais il s'agit simplement d'apprendre à un ordinateur à penser comme un joueur prudent qui prend en compte à la fois ses coups et ceux de son adversaire avant de prendre une décision.

Comprendre l'algorithme Minimax

Décrivons le fonctionnement de Minimax à l'aide d'un exemple simple de morpion. Imaginez que vous jouez le rôle de X et que l'ordinateur est O.

Comment pense l'ordinateur

Lorsque c'est le tour de l'ordinateur, il suit les étapes suivantes :

1. Examinez tous les mouvements possibles qu'il peut effectuer
2. Pour chaque mouvement, il imagine ce que vous pourriez faire ensuite
3. Il continue à réfléchir jusqu'à ce qu'il atteigne un point final (comme une victoire ou une égalité).
4. Il choisit le mouvement qui lui donne le plus de chances de gagner

Le score du jeu

L'ordinateur peut utiliser un système de notation simple :

• +10 points si l'ordinateur gagne
• -10 points si vous gagnez
• 0 point en cas d'égalité

Pensez-y comme à un arbre de possibilités :

• En haut se trouve le plateau de jeu actuel
• Chaque branche est un mouvement possible
• En bas, vous trouverez tous les résultats possibles

Le tour de rôle

L'ordinateur passe d'un mode de pensée à l'autre :

1. Mode de maximisation (tour de l'ordinateur) :

• Recherche les mouvements qui obtiennent le score le plus élevé
• Tentative de victoire ou de match nul

2. Mode minimisation (tour du joueur) :

• Suppose que vous ferez les mouvements qui obtiendront le score le plus bas.
• Préparez vos déplacements dans les meilleures conditions

Un exemple simple

Disons que c'est le tour de l'ordinateur (X) dans ce jeu :

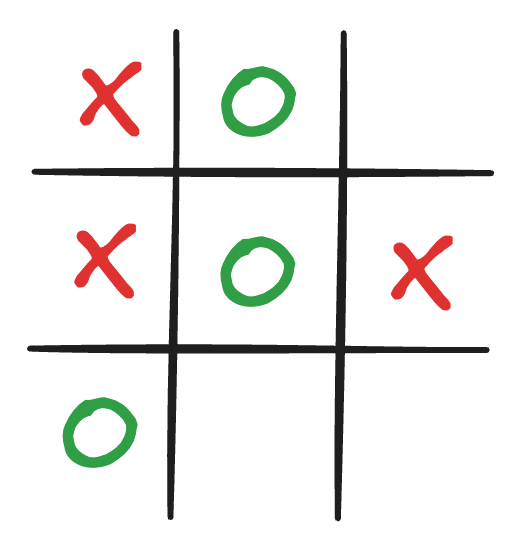
L'ordinateur va :

1. Vous voyez qu'il y a 3 emplacements vides à choisir
2. Pour chaque emplacement vide, il imagine tous les mouvements futurs possibles
3. Choisit le mouvement qui mène à son meilleur résultat
4. Dans ce cas, il devrait sélectionner le coin inférieur médian pour bloquer votre victoire.

Cette façon de penser à l'avance permet à l'ordinateur de jouer une partie parfaite de morpion à chaque fois !

Pseudocode de l'algorithme Minimax

Voyons comment écrire l'algorithme Minimax étape par étape. Ne vous inquiétez pas si vous êtes novice en matière de pseudocode - considérez-le comme un moyen d'écrire les étapes en langage clair avant de les transformer en code réel !

Explication étape par étape

La fonction Minimax a besoin de trois éléments principaux pour fonctionner :

1. Le plateau de jeu actuel
2. La profondeur (le nombre de coups d'avance que nous recherchons)
3. Qu'il s'agisse du tour du joueur maximisateur (ordinateur) ou du tour du joueur minimisateur (humain)

Voici à quoi ressemble le pseudocode de base :

function minimax(board, depth, isMaximizingPlayer):
   # First, check if the game is over
   if game is won:
       return +10 if computer wins, -10 if human wins
   if game is tied:
       return 0

   # If it's the computer's turn (maximizing)
   if isMaximizingPlayer:
       bestScore = -infinity
       for each empty spot on board:
           make the move
           score = minimax(board, depth + 1, false)
           undo the move
           bestScore = max(score, bestScore)
       return bestScore

   # If it's the human's turn (minimizing)
   else:
       bestScore = +infinity
       for each empty spot on board:
           make the move
           score = minimax(board, depth + 1, true)
           undo the move
           bestScore = min(score, bestScore)
       return bestScore

Alors que la plupart des exemples de pseudocode se lisent en anglais et sont parfaitement compréhensibles, l'exemple ci-dessus est différent car il utilise la récursivité. On parle de récursivité lorsqu'une fonction s'appelle elle-même à plusieurs reprises pour résoudre un problème plus important. Imaginez que vous vous regardez dans un miroir qui reflète un autre miroir : vous voyez la même image répétée plusieurs fois, de plus en plus petite à chaque fois.

Dans notre algorithme Minimax, nous avons besoin de la récursivité parce que nous essayons d'examiner tous les mouvements futurs possibles dans le jeu. Chaque fois que la fonction s'appelle elle-même, elle examine le prochain mouvement qui pourrait se produire. 

Cela nous aide à déterminer le meilleur mouvement en vérifiant toutes les possibilités de déroulement du jeu, comme un joueur très intelligent qui se dit "Si je fais ceci, alors ils pourraient faire cela, alors je pourrais faire ceci..." et ainsi de suite jusqu'à la fin du jeu. Pour en savoir plus sur la récursion, vous pouvez consulter notre tutoriel sur la récursion.

Exemple illustratif

Voyons comment cela fonctionne dans une situation de jeu simple :

1. Position de départ :

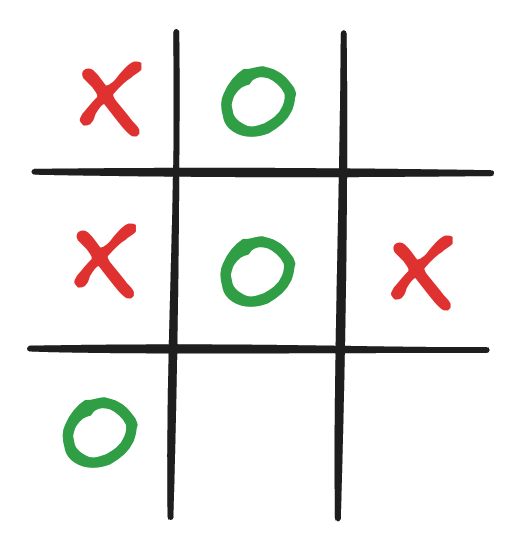
2. L'ordinateur réfléchit :

• "Si je place X dans n'importe quel endroit vide..."
• "Que ferait l'humain ensuite ?"
• "Et que pourrais-je faire après cela ?"
• "Quel mouvement me permet d'obtenir le meilleur score final ?

3. Pour chaque emplacement vide, l'ordinateur :

• Fait un geste
• Vérifie si le jeu est terminé
• Si ce n'est pas le cas, imaginez le meilleur mouvement de l'homme.
• Continue jusqu'à ce qu'il trouve une fin
• Choisit le mouvement avec le score le plus élevé

Pensez-y comme aux échecs : vous pensez toujours "Si je bouge ici, ils bougeront là, puis je pourrai bouger ici...", mais l'ordinateur peut penser à TOUS les mouvements possibles en même temps !

L'intérêt de cet algorithme est qu'il trouve toujours le meilleur coup possible, en supposant que les deux joueurs jouent parfaitement. C'est comme si vous aviez une boule de cristal qui vous montre tous les futurs possibles du jeu !

Implémentation de Minimax pour le Tic-tac-toe, étape par étape

Dans cette section, nous allons construire une IA de morpion imbattable alimentée par l'algorithme Mini-max en Python pur. Nous décomposerons la mise en œuvre en étapes simples et expliquerons l'intuition derrière chacune d'entre elles et comment elles s'intègrent dans l'image globale du jeu.

Étape 1 : Définition d'une classe TicTacToe

Tout d'abord, nous définissons une classe qui contient toute la logique et les méthodes dont nous avons besoin pour jouer au morpion avec nos ordinateurs :

class TicTacToe:
   def __init__(self):
       # Initialize empty board (using ' ' for empty squares)
       self.board = [" " for _ in range(9)]
       self.human_player = "O"
       self.ai_player = "X"

   def print_board(self):
       """Print the current state of the board"""
       for i in range(0, 9, 3):
           print(f"{self.board[i]} | {self.board[i+1]} | {self.board[i+2]}")
           if i < 6:
               print("---------")

   def available_moves(self):
       """Returns list of available moves (indices of empty squares)"""
       return [i for i, spot in enumerate(self.board) if spot == " "]

Ci-dessus, la méthode __init__ initialise un nouveau plateau de jeu sous la forme d'une liste de 9 cases vides (représentées par les espaces " "), les indices 0 à 8 représentant les positions du plateau de gauche à droite, de haut en bas. Il met également en place deux symboles de joueur - "O" pour le joueur humain et "X" pour l'IA.

La méthode print_board permet de visualiser l'état actuel de la carte. Il imprime la grille 3x3 avec des lignes de séparation entre les rangées, montrant les mouvements de chaque joueur dans leurs positions respectives.

La méthodeavailable_moves renvoie une liste de tous les mouvements valides qui peuvent encore être effectués. Pour ce faire, il vérifie quelles positions du tableau sont encore vides (contiennent un espace " ") et renvoie leurs indices. Cela sera crucial pour que l'algorithme minimax sache quels mouvements il peut prendre en compte.

Ces méthodes constituent la base sur laquelle nous nous appuierons pour créer notre joueur IA à l'aide de l'algorithme minimax.

Testons-les rapidement :

>>> game = TicTacToe()
>>> game.print_board()
  |   | 
---------
  |   | 
---------
  |   |

>>> game.available_moves()
[0, 1, 2, 3, 4, 5, 6, 7, 8]

Comme prévu, l'échiquier est vide pour le moment et tous les coups sont disponibles.

Étape 2 : Mise en place de méthodes pour effectuer un mouvement et vérifier l'état du plateau.

Ajoutons maintenant une méthode pour effectuer un déplacement :

class TicTacToe:
   ...
  
   def make_move(self, position, player):
       """Make a move on the board"""
       if self.board[position] == " ":
           self.board[position] = player
           return True
       return False

Nous avons ajouté la méthode make_move qui :

• Prend une position (0-8) et un symbole de joueur ("X" ou "O") en entrée.
• Vérifie si la position sélectionnée est vide (" ")
• Si vide, place le symbole du joueur et renvoie True
• Si la position est déjà prise, renvoie Faux sans effectuer de changement.

Effectuons quelques mouvements et vérifions les mouvements restants :

>>> game = TicTacToe()

>>> game.make_move(0, "X")
>>> game.make_move(1, "O")

>>> game.print_board()
 X | O | 
-----------
   |   | 
-----------
   |   |

>>> game.available_moves()
[2, 3, 4, 5, 6, 7, 8]

Le travail est bien fait. L'étape suivante consiste à ajouter une méthode permettant de vérifier si le tableau est plein :

class TicTacToe:
   ...

   def is_board_full(self):
       """Check if the board is full"""
       return " " not in self.board

is_board_full est une méthode booléenne qui vérifie s'il reste des espaces vides sur le plateau.

Ensuite, nous ajoutons une méthode pour vérifier si un état gagnant est atteint :

class TicTacToe:
   ...

   def check_winner(self):
       """Check if there's a winner. Returns winner symbol or None"""
       # Check rows
       for i in range(0, 9, 3):
           if self.board[i] == self.board[i + 1] == self.board[i + 2] != " ":
               return self.board[i]

       # Check columns
       for i in range(3):
           if self.board[i] == self.board[i + 3] == self.board[i + 6] != " ":
               return self.board[i]

       # Check diagonals
       if self.board[0] == self.board[4] == self.board[8] != " ":
           return self.board[0]
       if self.board[2] == self.board[4] == self.board[6] != " ":
           return self.board[2]

       return None

La méthode check_winner évalue l'état actuel du plateau de Tic-tac-toe pour déterminer s'il y a un gagnant. Il vérifie toutes les combinaisons gagnantes possibles :

1. Rangs (3 possibilités) :

• Première ligne (indices 0,1,2)
• Ligne médiane (indices 3,4,5)
• Rangée inférieure (indices 6,7,8)

2. Colonnes (3 possibilités) :

• Colonne de gauche (indices 0,3,6)
• Colonne centrale (indices 1,4,7)
• Colonne de droite (indices 2,5,8)

3. Diagonales (2 possibilités) :

• De haut en bas à gauche et de bas en haut à droite (indices 0,4,8)
• Du haut à droite au bas à gauche (indices 2,4,6)

Pour chaque combinaison, il vérifie si les trois positions contiennent le même symbole de joueur (X ou O) et ne sont pas des espaces vides. Si une combinaison gagnante est trouvée, elle renvoie le symbole du joueur gagnant. Si aucun gagnant n'est trouvé après avoir vérifié toutes les possibilités, il renvoie None.

Testons la fonction dans les États gagnants et non gagnants :

game = TicTacToe()

# Winning state
game.make_move(0, "X")
game.make_move(1, "X")
game.make_move(2, "X")

>>> game.print_board()
 X | X | X
-----------
   |   | 
-----------
   |   |

>>> game.check_winner()
'X'

game = TicTacToe()

# Non-winning state
game.make_move(0, "X")
game.make_move(1, "O")
game.make_move(2, "O")
game.make_move(3, "X")

>>> game.print_board()
 X | O | O
-----------
 X |   | 
-----------
   |   |

>>> game.check_winner() is None
True

Enfin, nous ajoutons une autre méthode booléenne pour spécifier si le jeu est terminé ou non :

class TicTacToe:
   ...

   def game_over(self):
       """Check if the game is over"""
       return self.check_winner() is not None or self.is_board_full()

La méthode renvoie True si le gagnant est trouvé ou si le tableau est plein.

À ce stade, nous avons construit tous les mécanismes de base du jeu :

• Le tableau est représenté par une liste de 9 carrés initialisés vides
• print_board() affiche visuellement l'état actuel du jeu
• available_moves() renvoie les indices des carrés vides
• make_move() place le symbole d'un joueur sur le plateau de jeu
• check_winner() examine les lignes, les colonnes et les diagonales pour gagner à chaque coup
• is_board_full() détermine s'il ne reste aucun mouvement
• game_over() combine le contrôle du vainqueur et le contrôle du tableau complet

Ces méthodes fournissent les bases nécessaires à la création d'un jeu jouable, en gérant toutes les opérations de base telles que l'exécution des mouvements et la détermination de l'état du jeu.

Vient maintenant la partie critique : donner à l'ordinateur le "cerveau" nécessaire pour jouer au jeu avec Minimax.

Étape 3 : Implémentation de Minimax pour le morpion

Maintenant, implémentons l'algorithme du jeu dans une nouvelle méthode :

class TicTacToe:
   ...

   def minimax(self, depth, is_maximizing):
       """
       Minimax algorithm implementation
       Returns the best score possible for the current board state
       """
       # Base cases
       winner = self.check_winner()
       if winner == self.ai_player:
           return 1
       if winner == self.human_player:
           return -1
       if self.is_board_full():
           return 0

La fonction prend deux paramètres :

• depth - Curse le nombre de niveaux de la récursion. Cela peut être utilisé pour limiter la profondeur de recherche pour les jeux très complexes, bien que pour le morpion nous n'ayons pas besoin de la limiter.
• is_maximizing - Indicateur booléen indiquant si nous recherchons actuellement le score maximum (tour de l'IA) ou le score minimum (tour de l'homme). Cette procédure alterne avec chaque appel récursif au fur et à mesure que les joueurs se succèdent.

Dans le corps de la fonction, nous commençons par définir les cas de base : Si la partie est gagnée par l'IA (winner == ai_player), nous retournons 1 car c'est le meilleur résultat possible pour l'IA. Si l'humain gagne (winner == human_player), nous renvoyons -1 car il s'agit du pire résultat pour l'IA. Si le tableau est plein et qu'il n'y a pas de gagnant, nous retournons 0 pour un tirage au sort.

def minimax(self, depth, is_maximizing):
   ...

   # if it is the maximizing player's turn (AI), we want to maximize the score
   if is_maximizing:
       best_score = float("-inf")
       for move in self.available_moves():
           # Make a calculating move
           self.board[move] = self.ai_player
           # Recursively call minimax with the next depth and the minimizing player
           score = self.minimax(depth + 1, False)
           # Reset the move
           self.board[move] = " "
           # Update the best score
           best_score = max(score, best_score)
       return best_score

Lorsque is_maximizing est True, nous simulons le tour de l'IA et nous voulons trouver le mouvement qui mène au score le plus élevé possible. Nous commençons par fixer best_score à l'infini négatif afin que tout score réel soit meilleur. Ensuite, pour chaque mouvement disponible, nous :

1. Placez temporairement le symbole de l'IA sur le plateau de jeu.
2. Évaluer récursivement ce qui se passerait si nous faisions ce mouvement en appelant minimax avec is_maximizing=False (puisque ce serait le tour de l'humain ensuite).
3. Annulez le déplacement temporaire pour rétablir l'état de la carte.
4. Gardez la trace du score le plus élevé que nous ayons vu jusqu'à présent en utilisant max()

Cela nous permet de vérifier tous les mouvements possibles de l'IA. Pour chaque coup, nous examinons ce qui pourrait se produire ensuite, jusqu'à ce que quelqu'un gagne ou que le jeu soit à égalité. Nous travaillons ensuite à rebours pour déterminer quel premier coup donne à l'IA la meilleure chance de gagner.

Maintenant, faisons la partie minimisation pour l'homme :

def minimax(self, depth, is_maximizing):
   ...

   # if it is the maximizing player's turn (AI), we want to maximize the score
   if is_maximizing:
       ...

   else:
       # if it is the minimizing player's turn (human), we want to minimize the score
       best_score = float("inf")
       for move in self.available_moves():
           # Make a calculating move
           self.board[move] = self.human_player
           # Recursively call minimax with the next depth and the maximizing player
           score = self.minimax(depth + 1, True)
           # Reset the move
           self.board[move] = " "
           # Update the best score
           best_score = min(score, best_score)
       return best_score

Lorsque is_maximizing est False, nous simulons le tour du joueur humain et nous voulons trouver le mouvement qui mène au score le plus bas possible (puisqu'un score élevé signifie que l'IA gagne). Nous partons de best_score comme d'une infinité positive, de sorte que tout score réel sera inférieur. Pour chaque mouvement disponible, nous :

1. Placez temporairement le symbole de l'homme sur le tableau.
2. Évaluer récursivement ce qui se passerait en appelant minimax avec is_maximizing=True (puisque ce serait le tour de l'IA ensuite).
3. Annulez le déplacement temporaire pour rétablir l'état de la carte.
4. Le cursus du score le plus bas que nous ayons connu avec l'utilisation de min()

Cela simule le joueur humain essayant de faire les meilleurs mouvements pour empêcher l'IA de gagner. L'humain souhaite minimiser le score car les scores positifs représentent des victoires de l'IA. En alternant les tours de maximisation et de minimisation, l'algorithme peut déterminer la séquence de mouvements optimale pour les deux joueurs.

Étape 4 : Trouver le meilleur mouvement pour l'IA à l'aide de Minimax

Maintenant que l'algorithme est prêt, nous avons besoin d'une autre méthode qui utilise la méthode minimax pour déterminer le meilleur coup pour l'IA après chaque coup humain :

class TicTacToe:
   ...

   def get_best_move(self):
       """Find the best move for AI using minimax"""
       best_score = float("-inf")
       best_move = None

       for move in self.available_moves():
           # Make a calculating move
           self.board[move] = self.ai_player
           # Recursively call minimax with the next depth and the minimizing player
           score = self.minimax(0, False)
           # Reset the move
           self.board[move] = " "

           # Update the best score
           if score > best_score:
               best_score = score
               best_move = move

       return best_move

La méthode get_best_move est chargée de déterminer le déplacement optimal du joueur IA à l'aide de l'algorithme minimax. Il fonctionne de la manière suivante :

1. En commençant par l'infini négatif comme meilleur score et en ne choisissant aucun mouvement

2. Pour chaque mouvement disponible sur le plateau :

• Placer temporairement le symbole de l'IA dans cette position
• L'utilisation de minimax pour évaluer la qualité de ce coup en simulant le reste du jeu
• Annuler le déménagement temporaire
• Si ce mouvement conduit à un meilleur score que ce que nous avons vu précédemment, nous mettons à jour à la fois le meilleur score et le meilleur mouvement.

3. Retourner enfin le mouvement qui a permis d'obtenir le score le plus élevé

Cette approche garantit que l'IA choisira le coup qui lui donne les meilleures chances de gagner, en supposant que le joueur humain joue lui aussi de manière optimale. La méthode prend en compte tous les états de jeu futurs possibles et choisit la voie qui maximise les chances de l'IA tout en minimisant les chances de victoire de l'humain.

Testons-le sur un exemple d'état de jeu :

game = TicTacToe()

# Make a couple of moves
game.make_move(0, "X")
game.make_move(1, "O")

# Print the board

>>> game.print_board()
X | O | 
---------
  |   | 
---------
  |   |

>>> game.get_best_move()
3

# AI moves
>>> game.make_move(3, "X")

# I move
>>> game.make_move(4, "O")
>>> game.print_board()
X | O | 
---------
X | O | 
---------
  |   |

# Get the best move for AI
>>> game.get_best_move()
6

Comme vous pouvez le voir, l'IA a trouvé la combinaison gagnante en se basant sur mes déplacements (il s'agissait d'un état factice, mais cela prouve que notre algorithme fonctionne).

Étape 5 : Mise en œuvre d'une boucle de jeu

Maintenant que nous avons implémenté et testé notre algorithme minimax, créons une boucle de jeu qui nous permettra de jouer contre l'IA.

class TicTacToe:

   ...

   def play_game(self):
       """Main game loop"""
       print("Welcome to Tic Tac Toe!")
       print("You are 'O' and the AI is 'X'")
       print("Enter positions (0-8) as shown below:")
       print("0 | 1 | 2")
       print("---------")
       print("3 | 4 | 5")
       print("---------")
       print("6 | 7 | 8")
       print("\n")

La méthode play_game commence par afficher un message de bienvenue et des instructions au joueur. Il montre que le joueur humain utilise "O" et que l'IA utilise "X". Il imprime ensuite une grille numérotée (0-8) pour indiquer au joueur quel numéro correspond à quelle position sur le plateau. Il est ainsi facile pour les joueurs de savoir exactement quel chiffre saisir pour le coup qu'ils souhaitent effectuer.

# ... the rest of the class
def play_game(self):
   ...

   # Randomly decide who goes first
   import random

   ai_turn = random.choice([True, False])

   while not self.game_over():
       self.print_board()

       if ai_turn:
           print("\nAI's turn...")
           move = self.get_best_move()
           self.make_move(move, self.ai_player)
       else:
           while True:
               try:
                   move = int(input("\nYour turn (0-8): "))
                   if 0 <= move <= 8 and self.make_move(move, self.human_player):
                       break
                   else:
                       print("Invalid move! Try again.")
               except ValueError:
                   print("Please enter a number between 0 and 8!")

       ai_turn = not ai_turn

Après avoir affiché les instructions initiales, le jeu entre dans sa boucle principale. Le jeu décide de manière aléatoire qui commence - l'IA ou le joueur humain - en utilisant random.choice([True, False]). Cela crée un élément d'équité et d'imprévisibilité au début de chaque partie.

La boucle principale du jeu se poursuit jusqu'à ce que game_over() renvoie True (quelqu'un a gagné ou le plateau est plein). Pendant chaque tour, l'état actuel du plateau est affiché à l'aide de print_board().

Si c'est le tour de l'IA (ai_turn est True), le programme :

1. Imprime un message indiquant que l'IA est en train de réfléchir
2. Appelle get_best_move() pour déterminer le mouvement optimal à l'aide de l'algorithme minimax.
3. Effectue le déplacement en plaçant le symbole de l'IA ("X") à la position choisie.

Si c'est le tour de l'humain (ai_turn est Faux), le programme :

1. Entre dans une boucle pour obtenir des données valides de la part du joueur2. Demande un numéro de déplacement entre 0 et 83. Valide l'entrée est :

• Un entier valide (en utilisant try/except)
• Dans la plage de validité 0-8
• Indique une position vide sur le tableau

4. Continue à demander jusqu'à ce qu'une entrée valide soit reçue. Effectue le déplacement en plaçant le symbole du joueur ("O") à la position choisie.

Après chaque tour, ai_turn est retourné à l'aide de not pour alterner entre les joueurs. Cela crée le flux de va-et-vient du jeu, chaque joueur jouant à tour de rôle jusqu'à ce que quelqu'un gagne ou que le jeu se termine par un match nul.

La validation des entrées garantit que le jeu ne peut pas se bloquer à cause d'une entrée invalide de l'utilisateur et fournit des messages d'erreur utiles pour guider le joueur afin qu'il entre les mouvements corrects. Cela permet de créer une expérience de jeu robuste et conviviale.

def play_game(self):
   ...
   # Game over
   self.print_board()
   winner = self.check_winner()
   if winner == self.ai_player:
       print("\nAI wins!")
   elif winner == self.human_player:
       print("\nCongratulations! You win!")
   else:
       print("\nIt's a tie!")

Lorsque le jeu se termine, l'état final du plateau est affiché à l'aide de print_board() et le gagnant est déterminé par check_winner(). Le jeu peut se terminer de trois façons :

1. L'IA gagne - Si check_winner() renvoie le symbole de l'IA ('X'), cela indique que l'IA a obtenu une ligne gagnante.
2. L'homme gagne - Si check_winner() renvoie le symbole de l'homme ('O'), cela indique que le joueur a obtenu une ligne gagnante.
3. Tirage au sort/égalité - Si aucun des deux joueurs n'a gagné mais que le plateau est plein, ce qui signifie qu'aucun autre coup n'est possible.

Le message approprié s'affiche pour annoncer le résultat du jeu. Cela permet au joueur de savoir clairement comment le jeu s'est terminé.

Étape 6 : Tout mettre en place

Il est maintenant temps de mettre tout le code que nous avons écrit jusqu'à présent dans un script Python avec ce qui suit if/main à la toute fin :

# Start the game
if __name__ == "__main__":
   game = TicTacToe()
   game.play_game()

Cela permet au jeu de démarrer dès que vous exécutez le script avec python script.py. Si vous vous êtes perdu parmi toutes les explications et les blocs de code, vous pouvez trouver le code complet du jeu dans ce GitHub gist.

Voici un exemple de jeu auquel j'ai participé :

❯ python tic-tac-toe.py
Welcome to Tic Tac Toe!
You are 'O' and the AI is 'X'
Enter positions (0-8) as shown below:
0 | 1 | 2
---------
3 | 4 | 5
---------
6 | 7 | 8


  |   | 
---------
  |   | 
---------
  |   | 

Your turn (0-8): 4
  |   | 
---------
  | O | 
---------
  |   | 

AI's turn...
X |   | 
---------
  | O | 
---------
  |   | 

Your turn (0-8): 5
X |   | 
----------
  | O | O
----------
  |   | 

AI's turn...
X |   | 
---------
X | O | O
---------
  |   | 

Your turn (0-8): 6
X |   | 
---------
X | O | O
---------
O |   | 

AI's turn...
X |   | X
---------
X | O | O
---------
O |   | 

Your turn (0-8): 1
X | O | X
---------
X | O | O
---------
O |   | 

AI's turn...
X | O | X
---------
X | O | O
---------
O | X | 

Your turn (0-8): 8
X | O | X
---------
X | O | O
---------
O | X | O

It's a tie!

N'oubliez pas que le morpion étant un jeu simple, vous n'avez aucune chance de battre l'IA. Soit vous êtes à égalité, soit vous perdez !

Formalisation de l'algorithme mini-maxi

Examinons maintenant la définition générale d'un algorithme au-delà de l'exemple simple du morpion.

L'algorithme Minimax peut être formellement défini comme une fonction récursive qui évalue les positions dans un jeu à somme nulle. Décortiquons ses composants formels et ses propriétés.

Définition mathématique

Pour un état de jeu s, la valeur minimax V(s) est définie comme suit :

V(s) =
   utility(s)                    if s is terminal
   max(V(s')) for all s' in S    if player = MAX
   min(V(s')) for all s' in S    if player = MIN

Où ?

• s' représente les états successeurs de s
• S est l'ensemble de tous les mouvements légaux à partir de l'état s
• utility(s) est la fonction d'évaluation des états terminaux

Propriétés principales

1. Une information parfaite

• Tous les joueurs ont une connaissance complète de l'état du jeu
• Pas d'informations cachées ni d'éléments fortuits
• Résultats déterministes

2. La nature à somme nulle

• Le gain d'un joueur est exactement égal à la perte de l'autre joueur.
• La somme des utilités de tous les joueurs est toujours égale à zéro
• Pour les jeux à deux joueurs, les utilités sont généralement {-1, 0, 1}

3. Jeu optimal

• On suppose que les deux joueurs prennent des décisions optimales
• Garantit le meilleur résultat possible en cas de jeu parfait
• Conduit à un équilibre de Nash en termes de théorie des jeux.

Analyse de la complexité

Complexité temporelle : O(b^m)

• b = facteur de branchement (nombre de coups légaux à chaque état)
• m = profondeur maximale de l'arbre de jeu

Complexité de l'espace : O(bm)

• Nécessite le stockage de l'état du jeu à chaque niveau
• Peut être optimisé par un approfondissement itératif

Fonction d'évaluation

Pour les états non terminaux, la fonction d'évaluation f(s) doit :

1. Corrélation avec la probabilité de gagner
2. Être efficace sur le plan informatique
3. Maintenir une échelle cohérente tout au long du jeu

La définition formelle :

f(s) = w₁x₁ + w₂x₂ + ... + wₙxₙ

Où ?

• wᵢ sont les poids des différentes caractéristiques
• xᵢ sont les valeurs des caractéristiques de l'état du jeu
• n est le nombre de caractéristiques évaluées

Garantie d'optimalité

L'algorithme Minimax garantit un jeu optimal dans ces conditions :

1. Une information parfaite
2. Résultats déterministes
3. Recherche complète des états terminaux
4. Évaluation précise de l'état des terminaux

Il est donc particulièrement adapté aux jeux d'échecs, de morpion et de dames, pour lesquels ces conditions sont remplies.

Variantes avancées et limites

Si Minimax est parfait pour les jeux simples comme le morpion, il rencontre quelques problèmes avec les jeux plus importants. Voyons comment nous pouvons l'améliorer et quels sont ses points faibles.

Rendre Minimax plus rapide : Taille alpha-bêta

Imaginez que vous jouez aux échecs et que vous réfléchissez à vos mouvements. Si vous avez trouvé un coup gagnant, vous n'avez pas besoin de vérifier tous les autres coups possibles, n'est-ce pas ? L'élagage alpha-bêta fonctionne de la même manière - il aide l'ordinateur à ne pas vérifier les mouvements dont nous savons déjà qu'ils ne seront pas meilleurs que ceux que nous avons trouvés.

Pensez-y comme suit :

• Vous cherchez la barre chocolatée la moins chère
• Vous avez 1 $ à dépenser
• Si vous trouvez une barre chocolatée à 50 cents, vous pouvez ne pas regarder les barres chocolatées qui coûtent plus d'un dollar.
• Cela vous permet de gagner du temps !

Limites de profondeur : Ne pas regarder trop loin

Dans les grands jeux comme les échecs, il y a trop de mouvements possibles pour les vérifier tous. Nous ajoutons donc une limite de profondeur :

1. Ne regardez que 4 ou 5 coups à l'avance au lieu de regarder jusqu'à la fin.
2. Faites une bonne estimation de la qualité de la position à ce moment-là.
3. Choisissez le meilleur mouvement en fonction de ces suppositions

Vous ne pouvez pas planifier tous vos mouvements jusqu'à la fin de la partie, mais vous pouvez le faire quelques fois à l'avance !

Là où Minimax se bat

Minimax n'est pas parfait. Voici ses principaux problèmes :

1. Trop de choix

• Les jeux comme le Go ont beaucoup trop de mouvements possibles
• Même les ordinateurs rapides ne peuvent pas tous les vérifier
• C'est pourquoi nous avons besoin d'autres méthodes pour les jeux vraiment complexes

2. Problèmes de temps

• Plus vous regardez vers l'avant, plus cela prend du temps.
• Aux échecs, les ordinateurs ne peuvent pas examiner tous les coups possibles
• Ils doivent faire preuve d'intelligence dans le choix des mouvements à vérifier

3. Pas terrible pour les jeux incertains

• Le Minimax fonctionne mieux lorsque vous pouvez tout voir
• Il n'est pas adapté aux jeux de cartes où vous ne savez pas quelles sont les cartes des autres.
• Il ne peut pas bien gérer les événements aléatoires (comme les jets de dés).

Des solutions modernes

L'IA des jeux d'aujourd'hui combine souvent le Minimax avec d'autres techniques intéressantes :

1. Apprentissage automatique

• Les ordinateurs peuvent apprendre en regardant de nombreux jeux
• Cela leur permet de mieux deviner les bons coups.
• Des jeux comme AlphaGo utilisent cette méthode pour battre des champions humains.

2. Reconnaissance des formes

• Au lieu de vérifier chaque mouvement, recherchez des modèles
• Tout comme les joueurs humains reconnaissent les bons coups
• L'ordinateur est ainsi beaucoup plus rapide

3. Banque de mémoire

• Se souvenir de positions déjà vues
• Ne perdez pas de temps à calculer deux fois la même chose
• C'est comme si vous disposiez d'une antisèche de bons gestes !

Le plus intéressant ? Ces améliorations permettent aux ordinateurs de jouer à des jeux presque aussi bien que les humains, et parfois même mieux ! Mais n'oubliez pas que même avec tous ces ajouts fantaisistes, Minimax reste la base qui permet à tout de fonctionner.

Conclusion

Dans ce tutoriel, nous avons exploré l'algorithme Minimax depuis ses concepts de base jusqu'à sa mise en œuvre pratique. Voici ce que nous avons appris :

1. Concepts de base

• Comment Minimax aide les ordinateurs à prendre des décisions dans les jeux
• La différence entre les joueurs qui minimisent et ceux qui maximisent
• Pourquoi on parle de "minimax" et comment cela fonctionne-t-il ?

2. Compétences en matière de mise en œuvre

• Construire un jeu de morpion à partir de zéro
• Écrire l'algorithme Minimax en Python
• Test et débogage de la logique du jeu

3. Thèmes avancés

• Rendre l'algorithme plus rapide grâce à l'élagage Alpha-Beta
• Gestion des limitations dans les jeux complexes
• Améliorations modernes grâce à l'apprentissage automatique

Quelle est la prochaine étape ?

L'algorithme Minimax n'est qu'une pièce du puzzle de l'IA. Si vous souhaitez en savoir plus sur l'IA et les algorithmes, voici quelques ressources intéressantes pour poursuivre votre voyage :

1. Algorithmes associés

• Tutoriel sur l'algorithme A*- Découvrez les algorithmes de recherche de chemin
• Guide du renforcement du gradient- Explorer les algorithmes d'apprentissage automatique

2. Applications de l'apprentissage automatique

• Cas d'utilisation de l'apprentissage automatique- Découvrez des applications réelles

3. Des cursus d'apprentissage complets

• Développement d'applications d'IA- Élaborer des projets pratiques d'IA
• Principes de l'IA- Maîtriser les bases de l'IA

N'oubliez pas que, que vous construisiez un simple jeu ou un système d'intelligence artificielle complexe, la compréhension d'algorithmes tels que Minimax vous donne une base solide pour aborder des sujets plus avancés en matière d'intelligence artificielle. Continuez à vous entraîner, à apprendre et, surtout, à coder !