L'algorithme A* : Un guide complet

Les algorithmes de traversée de graphes sont fondamentaux pour de nombreuses applications informatiques, du développement de jeux à la robotique. Ces algorithmes sont conçus pour explorer et naviguer dans les graphes, qui sont des structures de données composées de nœuds (sommets) et d'arêtes. Parmi ces algorithmes, l'algorithme A* se distingue par son efficacité et sa polyvalence dans la recherche de chemins optimaux.

L'algorithme A* est un algorithme de recherche informée, ce qui signifie qu'il utilise une fonction heuristique pour guider sa recherche vers l'objectif. Cette fonction heuristique estime le coût pour atteindre l'objectif à partir d'un nœud donné, ce qui permet à l'algorithme de donner la priorité aux chemins prometteurs et d'éviter d'explorer les chemins inutiles.

Dans cet article, nous verrons les concepts clés de l'algorithme A*, son implémentation en Python, ses applications, ainsi que ses avantages et ses limites.

Pour en savoir plus sur la programmation Python, consultez notre Cours d'introduction à Python pour les développeurs cours.

Qu'est-ce que l'algorithme A* ?

L'algorithme A* est un algorithme puissant et largement utilisé de traversée de graphe et de recherche de chemin. Il permet de trouver le chemin le plus court entre un nœud de départ et un nœud d'arrivée dans un graphe pondéré. 

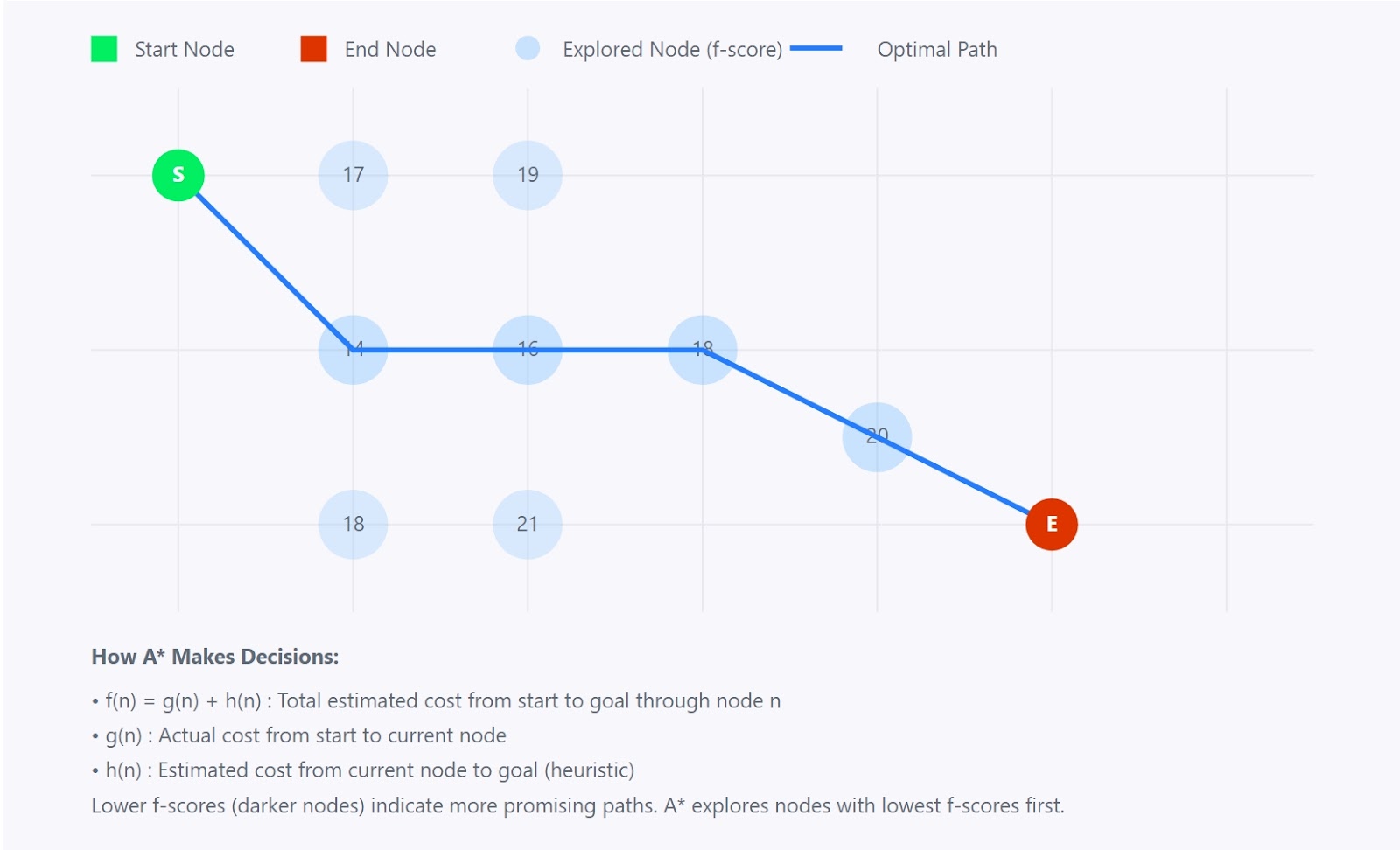
Algorithme A*

Comment fonctionne l'algorithme A* ?

L'algorithme A* combine les meilleurs aspects de deux autres algorithmes :

1. Algorithme de Dijkstra: Cet algorithme trouve le chemin le plus court vers tous les nœuds à partir d'un seul nœud source.
2. Recherche gourmande de la meilleure solution en premier : Cet algorithme explore le nœud qui semble le plus proche de l'objectif, sur la base d'une fonction heuristique.

Imaginez que vous essayez de trouver l'itinéraire le plus court entre deux villes sur une carte. Alors que l'algorithme de Dijkstra explore dans toutes les directions et que la recherche Best-First se dirige directement vers la destination (en manquant potentiellement des raccourcis), l'algorithme A* fait quelque chose de plus intelligent. Il prend en compte ces deux aspects :

• La distance déjà parcourue depuis le départ
• Une estimation intelligente de la distance restante jusqu'à l'objectif

Cette combinaison permet à A* de prendre des décisions éclairées sur la voie à suivre, ce qui la rend à la fois efficace et précise.

Principaux éléments

Pour comprendre l'algorithme A*, vous devez vous familiariser avec ces concepts fondamentaux :

• Nœuds: Points dans votre graphique (comme les intersections sur une carte)
• Bords: Connexions entre les nœuds (comme des routes reliant des intersections)
• Coût du chemin: Le coût réel du déplacement d'un nœud à l'autre
• Heuristique: Coût estimé de n'importe quel nœud jusqu'à l'objectif
• Espace de recherche: La collection de tous les chemins possibles à explorer

Dans la section suivante, nous approfondirons ces concepts et verrons comment A* les utilise pour trouver des chemins optimaux.

Concepts clés de la recherche A*

L'efficacité de l'algorithme A* provient de son évaluation intelligente des chemins à l'aide de trois composants clés : g(n), h(n) et f(n). Ces éléments se conjuguent pour orienter le processus de recherche vers les voies les plus prometteuses.

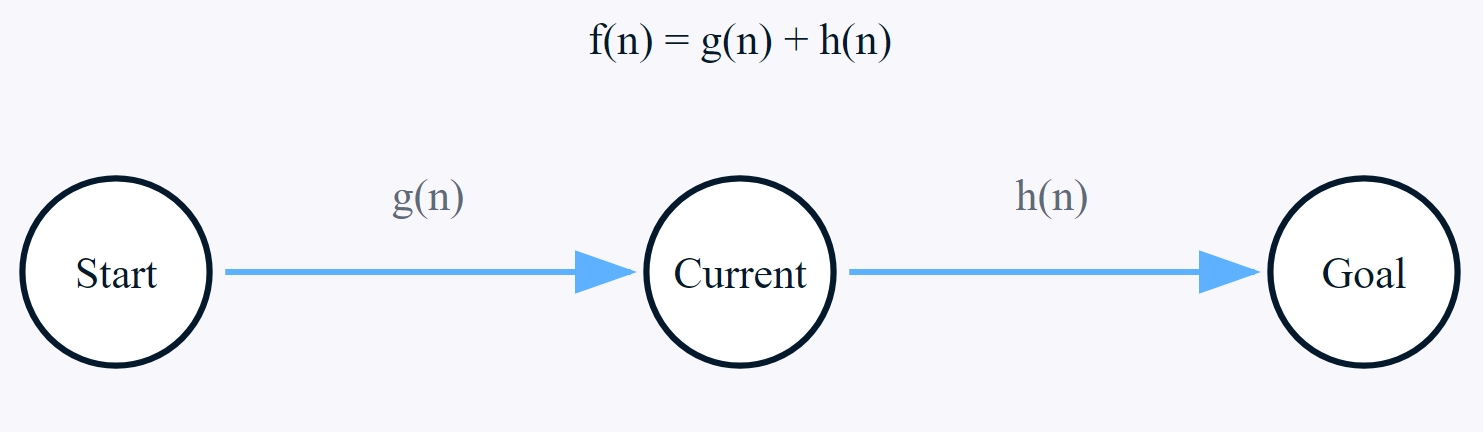
Algorithme A* Fonction de coût

Comprendre les fonctions de coût

Coût du chemin g(n)

La fonction de coût du chemin g(n) représente la distance exacte et connue entre le nœud de départ et la position actuelle dans notre recherche. Contrairement aux valeurs estimées, ce coût est précis et calculé en additionnant tous les poids des arêtes individuelles qui ont été parcourues le long du chemin choisi. 

Mathématiquement, pour un chemin passant par les nœuds n0(nœud de départ) à nk​ (nœud actuel), nous pouvons exprimer g(n) comme suit :

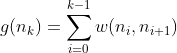
Où ?

• w(n_i,n_i+1) représente le poids de l'arête reliant le nœud ni au nœud n_i+1​.

Au fur et à mesure que nous nous déplaçons dans le graphique, cette valeur s'accumule, ce qui nous donne une mesure claire des ressources réelles (qu'il s'agisse de la distance, du temps ou de toute autre mesure) que nous avons dépensées pour atteindre notre position actuelle.

Fonction heuristique h(n)

La fonction heuristique h(n) fournit une estimation du coût entre le nœud actuel et le nœud cible, agissant comme une "supposition éclairée" de l'algorithme sur le chemin restant à parcourir. 

Mathématiquement, pour un nœud n donné, l'estimation heuristique doit satisfaire à la condition suivante h(n)≤h*(n) où h*(n) est le coût réel de l'objectif, ce qui le rend admissible en ne surestimant jamais le coût réel.

Dans les problèmes de type grille ou carte, les fonctions heuristiques courantes comprennent la distance de Manhattan et la distance euclidienne. Pour les coordonnées (x₁,y₁) du nœud actuel et (x₂,y₂) du nœud cible, ces distances sont calculées comme suit :

Distance de Manhattan

Distance euclidienne

Coût total estimé f(n)

Le coût total estimé f(n) est la pierre angulaire du processus décisionnel de l'algorithme A*, qui combine à la fois le coût réel du chemin et l'estimation heuristique pour évaluer le potentiel de chaque nœud. Pour tout nœud n, ce coût est calculé comme suit :

Où ?

• g(n) représente le coût réel entre le point de départ et le nœud actuel,
• h(n) représente le coût estimé entre le nœud actuel et l'objectif.

L'algorithme algorithme utilise cette valeur combinée pour choisir stratégiquement le nœud à explorer ensuite, en sélectionnant toujours le nœud ayant la plus faible valeur de f(n) la plus faible de la liste ouverte, assurant ainsi un équilibre optimal entre les coûts connus et les distances restantes estimées.

Gestion des listes de nœuds

L'algorithme A* tient à jour deux listes essentielles

Liste ouverte :

• Contient les nœuds qui doivent être évalués
• Classés par valeur f(n) (la plus faible en premier)
• De nouveaux nœuds sont ajoutés au fur et à mesure de leur découverte.

Liste fermée :

• Contient des nœuds déjà évalués
• Permet d'éviter la réévaluation des nœuds
• Utilisé pour reconstruire le chemin final

L'algorithme sélectionne continuellement le nœud ayant la plus faible valeur de f(n) de la liste ouverte, l'évalue et le déplace vers la liste fermée jusqu'à ce qu'il atteigne le nœud cible ou détermine qu'aucun chemin n'existe.

Pseudocode de l'algorithme de recherche A*

Maintenant que nous avons compris les éléments fondamentaux de l'A*, voyons comment ils s'articulent en pratique. La mise en œuvre de l'algorithme peut être décomposée en étapes claires et logiques qui transforment ces concepts en une solution de recherche de chemin opérationnelle.

Voici comment fonctionne l'algorithme, étape par étape :

function A_Star(start, goal):
    // Initialize open and closed lists
    openList = [start]          // Nodes to be evaluated
    closedList = []            // Nodes already evaluated
    
    // Initialize node properties
    start.g = 0                // Cost from start to start is 0
    start.h = heuristic(start, goal)  // Estimate to goal
    start.f = start.g + start.h       // Total estimated cost
    start.parent = null              // For path reconstruction
    while openList is not empty:
        // Get node with lowest f value - implement using a priority queue
       // for faster retrieval of the best node
        current = node in openList with lowest f value
        
        // Check if we've reached the goal
        if current = goal:
            return reconstruct_path(current)
            
        // Move current node from open to closed list
        remove current from openList
        add current to closedList
        
        // Check all neighboring nodes
        for each neighbor of current:
            if neighbor in closedList:
                continue  // Skip already evaluated nodes
                
            // Calculate tentative g score
            tentative_g = current.g + distance(current, neighbor)
            
            if neighbor not in openList:
                add neighbor to openList
            else if tentative_g >= neighbor.g:
                continue  // This path is not better
                
            // This path is the best so far
            neighbor.parent = current
            neighbor.g = tentative_g
            neighbor.h = heuristic(neighbor, goal)
            neighbor.f = neighbor.g + neighbor.h
    
    return failure  // No path exists
function reconstruct_path(current):
    path = []
    while current is not null:
        add current to beginning of path
        current = current.parent
    return path

Décortiquons chaque élément de cette mise en œuvre :

Phase d'initialisation

L'algorithme commence par établir deux listes essentielles :

• La liste ouverte commence par le nœud de départ
• La liste fermée commence vide

Chaque nœud stocke quatre éléments d'information essentiels :

• g : Le coût réel à partir du nœud de départ
• h : Le coût estimé de l'objectif
• f : La somme de g et h
• parent : Référence au nœud précédent (pour la reconstruction du chemin)

Boucle principale

Le cœur de l'A* est sa boucle principale, qui se poursuit jusqu'à ce que l'un ou l'autre des éléments suivants soit présent :

• L'objectif est atteint (succès)
• La liste ouverte devient vide (échec - aucun chemin n'existe)

Au cours de chaque itération, l'algorithme :

1. Sélectionne le nœud le plus prometteur (valeur f la plus basse) dans la liste ouverte.
2. Déplace le dossier vers la liste des dossiers clos
3. Examine tous les nœuds voisins

Évaluation des voisins

Pour chaque voisin, l'algorithme :

• Ignore les nœuds qui figurent déjà dans la liste des nœuds fermés
• Calcul d'un score g provisoire
• Met à jour les valeurs des nœuds si un meilleur chemin est trouvé
• Ajoute de nouveaux nœuds à la liste ouverte

Reconstruction du chemin

Une fois l'objectif atteint, l'algorithme remonte les références parentales pour construire le chemin optimal entre le point de départ et l'objectif.

Cette approche systématique garantit que A* trouvera toujours le chemin optimal si :

1. La fonction heuristique est admissible (elle ne surestime jamais)
2. Un chemin existe réellement entre les nœuds de départ et d'arrivée.

Dans la section suivante, nous traduirons ce pseudocode en une implémentation pratique en Python, avec des visualisations pour vous aider à comprendre comment l'algorithme explore l'espace de recherche.

Mise en œuvre de l'algorithme A* en Python

Maintenant que nous avons compris la théorie et le pseudocode, mettons en œuvre A* en Python. Nous créerons une mise en œuvre pratique que vous pourrez utiliser comme base pour vos propres projets. Pour rendre cela concret, nous mettrons en œuvre l'algorithme sur une grille 2D - un scénario courant dans les jeux et les applications robotiques.

Étape 1 : Fonctions essentielles et importations

Nous commençons par importer les bibliothèques nécessaires et par créer une structure de nœuds qui stockera les informations relatives à la position et au cheminement pour chaque point de notre espace de recherche.

from typing import List, Tuple, Dict, Set
import numpy as np
import heapq
from math import sqrt
def create_node(position: Tuple[int, int], g: float = float('inf'), 
                h: float = 0.0, parent: Dict = None) -> Dict:
    """
    Create a node for the A* algorithm.
    
    Args:
        position: (x, y) coordinates of the node
        g: Cost from start to this node (default: infinity)
        h: Estimated cost from this node to goal (default: 0)
        parent: Parent node (default: None)
    
    Returns:
        Dictionary containing node information
    """
    return {
        'position': position,
        'g': g,
        'h': h,
        'f': g + h,
        'parent': parent
    }

Étape 2 : Fonctions d'assistance

Pour soutenir notre algorithme de recherche de chemin, nous allons créer plusieurs fonctions d'aide. Tout d'abord, nous allons implémenter une fonction permettant de calculer les distances entre les points à l'aide de la distance euclidienne.

Ensuite, nous ajouterons une fonction pour trouver les positions voisines valides dans notre grille, en vérifiant soigneusement les limites et les obstacles. Enfin, nous créerons une fonction qui nous aidera à reconstruire le chemin une fois que nous aurons trouvé notre objectif.

def calculate_heuristic(pos1: Tuple[int, int], pos2: Tuple[int, int]) -> float:
    """
    Calculate the estimated distance between two points using Euclidean distance.
    """
    x1, y1 = pos1
    x2, y2 = pos2
    return sqrt((x2 - x1)**2 + (y2 - y1)**2)
def get_valid_neighbors(grid: np.ndarray, position: Tuple[int, int]) -> List[Tuple[int, int]]:
    """
    Get all valid neighboring positions in the grid.
    
    Args:
        grid: 2D numpy array where 0 represents walkable cells and 1 represents obstacles
        position: Current position (x, y)
    
    Returns:
        List of valid neighboring positions
    """
    x, y = position
    rows, cols = grid.shape
    
    # All possible moves (including diagonals)
    possible_moves = [
        (x+1, y), (x-1, y),    # Right, Left
        (x, y+1), (x, y-1),    # Up, Down
        (x+1, y+1), (x-1, y-1),  # Diagonal moves
        (x+1, y-1), (x-1, y+1)
    ]
    
    return [
        (nx, ny) for nx, ny in possible_moves
        if 0 <= nx < rows and 0 <= ny < cols  # Within grid bounds
        and grid[nx, ny] == 0                # Not an obstacle
    ]
def reconstruct_path(goal_node: Dict) -> List[Tuple[int, int]]:
    """
    Reconstruct the path from goal to start by following parent pointers.
    """
    path = []
    current = goal_node
    
    while current is not None:
        path.append(current['position'])
        current = current['parent']
        
    return path[::-1]  # Reverse to get path from start to goal

Étape 3 : Mise en œuvre de l'algorithme A* principal

Mettons maintenant en œuvre notre algorithme. Nous utiliserons une file d'attente prioritaire pour nous assurer que nous explorons toujours les chemins les plus prometteurs en premier. 

Notre algorithme maintient deux ensembles : un ensemble ouvert pour les nœuds que nous devons encore explorer et un ensemble fermé pour les nœuds que nous avons déjà vérifiés. 

Au fur et à mesure que nous explorons la grille, nous mettons continuellement à jour les coûts des chemins lorsque nous trouvons de meilleurs itinéraires, jusqu'à ce que nous atteignions notre objectif.

def find_path(grid: np.ndarray, start: Tuple[int, int], 
              goal: Tuple[int, int]) -> List[Tuple[int, int]]:
    """
    Find the optimal path using A* algorithm.
    
    Args:
        grid: 2D numpy array (0 = free space, 1 = obstacle)
        start: Starting position (x, y)
        goal: Goal position (x, y)
    
    Returns:
        List of positions representing the optimal path
    """
    # Initialize start node
    start_node = create_node(
        position=start,
        g=0,
        h=calculate_heuristic(start, goal)
    )
    
    # Initialize open and closed sets
    open_list = [(start_node['f'], start)]  # Priority queue
    open_dict = {start: start_node}         # For quick node lookup
    closed_set = set()                      # Explored nodes
    
    while open_list:
        # Get node with lowest f value
        _, current_pos = heapq.heappop(open_list)
        current_node = open_dict[current_pos]
        
        # Check if we've reached the goal
        if current_pos == goal:
            return reconstruct_path(current_node)
            
        closed_set.add(current_pos)
        
        # Explore neighbors
        for neighbor_pos in get_valid_neighbors(grid, current_pos):
            # Skip if already explored
            if neighbor_pos in closed_set:
                continue
                
            # Calculate new path cost
            tentative_g = current_node['g'] + calculate_heuristic(current_pos, neighbor_pos)
            
            # Create or update neighbor
            if neighbor_pos not in open_dict:
                neighbor = create_node(
                    position=neighbor_pos,
                    g=tentative_g,
                    h=calculate_heuristic(neighbor_pos, goal),
                    parent=current_node
                )
                heapq.heappush(open_list, (neighbor['f'], neighbor_pos))
                open_dict[neighbor_pos] = neighbor
            elif tentative_g < open_dict[neighbor_pos]['g']:
                # Found a better path to the neighbor
                neighbor = open_dict[neighbor_pos]
                neighbor['g'] = tentative_g
                neighbor['f'] = tentative_g + neighbor['h']
                neighbor['parent'] = current_node
    
    return []  # No path found

Étape 4 : Visualisation

Créons maintenant une fonction de visualisation. Cela nous permettra de voir notre grille avec les obstacles éventuels, de dessiner notre trajectoire optimale calculée et de marquer clairement nos positions de départ et d'arrivée.

import matplotlib.pyplot as plt
def visualize_path(grid: np.ndarray, path: List[Tuple[int, int]]):
    """
    Visualize the grid and found path.
    """
    plt.figure(figsize=(10, 10))
    plt.imshow(grid, cmap='binary')
    
    if path:
        path = np.array(path)
        plt.plot(path[:, 1], path[:, 0], 'b-', linewidth=3, label='Path')
        plt.plot(path[0, 1], path[0, 0], 'go', markersize=15, label='Start')
        plt.plot(path[-1, 1], path[-1, 0], 'ro', markersize=15, label='Goal')
    
    plt.grid(True)
    plt.legend(fontsize=12)
    plt.title("A* Pathfinding Result")
    plt.show()

Exemple d'utilisation

Voici comment utiliser la mise en œuvre :

# Create a sample grid
grid = np.zeros((20, 20))  # 20x20 grid, all free space initially
# Add some obstacles
grid[5:15, 10] = 1  # Vertical wall
grid[5, 5:15] = 1   # Horizontal wall
# Define start and goal positions
start_pos = (2, 2)
goal_pos = (18, 18)
# Find the path
path = find_path(grid, start_pos, goal_pos)
if path:
    print(f"Path found with {len(path)} steps!")
    visualize_path(grid, path)
else:
    print("No path found!")

Sortie

Chemin trouvé avec 22 étapes !

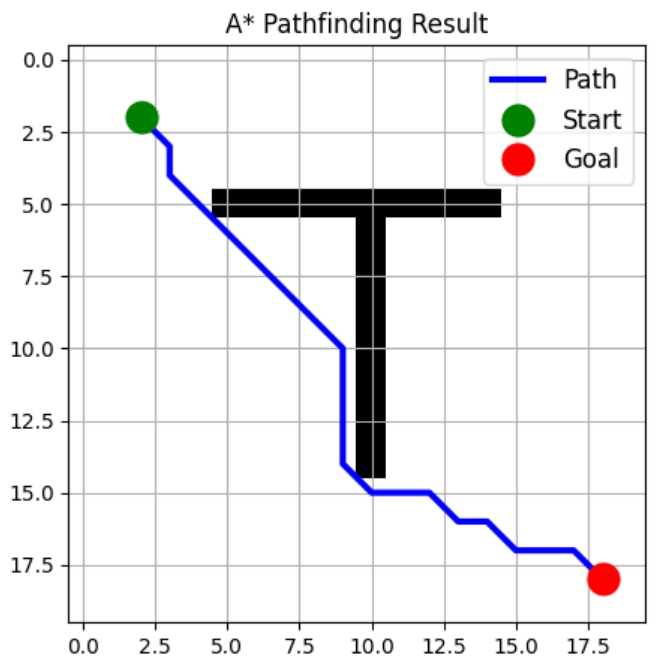
Cette mise en œuvre est à la fois efficace et extensible. Vous pouvez facilement le modifier :

• Utiliser différentes fonctions heuristiques
• Soutenir différents types de mouvements
• Manipuler les grilles pondérées
• Inclure des contraintes supplémentaires

Dans la section suivante, nous examinerons quelques applications pratiques de cet algorithme et verrons comment il est utilisé dans des scénarios réels.

Applications de l'algorithme de recherche A*

L'efficacité et la flexibilité de l'algorithme A* en font un outil précieux dans de nombreux domaines. Voici les principaux domaines dans lesquels il excelle :

1. Jeux vidéo et divertissement

L'algorithme de recherche A* est largement utilisé dans le développement de jeux vidéo en raison de ses capacités optimales de recherche de chemin. Il améliore l'expérience du joueur en permettant des mouvements de personnages plus réalistes et plus réactifs.

• Le cheminement des personnages dans les jeux de stratégie: A* aide les personnages à trouver le chemin le plus court ou le plus sûr vers une cible, ce qui est crucial dans les jeux de stratégie en temps réel (STR) où les unités doivent contourner efficacement les obstacles et les ennemis.
• Mouvement des PNJ dans les environnements ouverts: Les personnages non jouables (PNJ) utilisent l'A* pour naviguer dans des univers de jeu vastes et dynamiques, ce qui leur permet d'atteindre des objectifs tout en évitant les obstacles et les autres personnages.
• Planification tactique en temps réel dans les scénarios de combat: A* est utilisé pour calculer l'efficacité du mouvement et du positionnement des unités pendant le combat, en veillant à ce que les personnages puissent atteindre rapidement les endroits avantageux tout en évitant les dangers.
• Résolution de labyrinthes dans les jeux de puzzle: A* est un algorithme efficace pour naviguer dans des labyrinthes complexes, offrant aux joueurs un défi attrayant en alimentant des adversaires dynamiques qui résolvent des labyrinthes ou en fournissant des indices.

2. Systèmes de navigation

A* est largement utilisé dans les systèmes de navigation pour optimiser les itinéraires, en tenant compte de divers facteurs tels que la distance et les obstacles potentiels.

• Planification d'itinéraires dans les applications GPS: A* trouve l'itinéraire le plus court et le plus rapide entre deux points, ce qui en fait un composant essentiel des logiciels GPS utilisés par des millions de personnes dans le monde.
• Services de navigation en fonction du trafic: Dans les applications de navigation modernes, l'A* est combiné à des données de trafic en temps réel pour suggérer le meilleur itinéraire, en minimisant la durée du voyage et en évitant les routes encombrées.
• Optimisation des itinéraires des transports publics: A* peut aider à trouver des itinéraires optimaux qui intègrent plusieurs modes de transport public, en veillant à ce que les utilisateurs effectuent des transferts efficaces.
• Systèmes de navigation intérieure: L'A* est également utilisé pour la navigation intérieure, par exemple dans les aéroports ou les grands centres commerciaux, où il aide à guider les utilisateurs dans des environnements complexes comportant de nombreux niveaux et obstacles.

3. Robotique et automatisation

L'algorithme A* est crucial pour la robotique, où l'efficacité des mouvements est essentielle à la productivité et à la sécurité.

• Planification de la trajectoire d'un véhicule autonome: Les voitures autonomes utilisent l'A* pour naviguer sur les routes, en prenant des décisions en temps réel sur la manière de se déplacer d'un point A à un point B tout en évitant les collisions et en respectant le code de la route.
• Navigation des robots d'entrepôt: Dans les entrepôts automatisés, les robots s'appuient sur A* pour naviguer efficacement entre les rayonnages de stockage afin de prélever et de placer les articles, en minimisant les retards et en évitant les collisions avec d'autres robots.
• Optimisation de la trajectoire de vol des drones: A* aide les drones à planifier des trajectoires de vol efficaces, que ce soit pour la livraison, l'arpentage ou les loisirs, en veillant à ce qu'ils évitent les obstacles et suivent des itinéraires optimaux.
• Planification des mouvements des robots de fabrication: Dans les usines, l'A* est utilisé pour permettre aux robots de se déplacer sans problème entre les postes de travail, en évitant les collisions avec d'autres machines et en maintenant la productivité.

4. Systèmes de réseaux

L'A* est également appliqué à l'optimisation des opérations de réseau, où l'efficacité de l'utilisation des ressources et du routage est primordiale.

• Routage de paquets réseau: A* est utilisé pour déterminer le chemin le plus efficace pour les paquets de données à travers un réseau, garantissant une latence minimale et une grande fiabilité.
• Allocation de ressources dans les systèmes distribués: A* contribue à l'optimisation de l'allocation des ressources, ce qui permet aux systèmes distribués de répartir efficacement les tâches entre les différents nœuds tout en minimisant les frais généraux.
• Conception des circuits imprimés: Lors de la conception de cartes de circuits imprimés (PCB), A* peut être utilisé pour déterminer les chemins optimaux pour les traces électriques, garantissant ainsi une interférence minimale et une disposition efficace.
• Optimisation du routage des câbles réseau: A* est utilisé dans la conception d'infrastructures de réseaux physiques, pour trouver les itinéraires les plus efficaces pour les câbles afin de minimiser les coûts et de maximiser les performances.

Ce qui rend A* particulièrement précieux, c'est sa capacité d'adaptation grâce à des fonctions heuristiques personnalisées, qui permettent d'optimiser différents paramètres tels que la distance, le temps ou la consommation d'énergie.

Dans la section suivante, nous examinerons quelques défis courants et des techniques d'optimisation pour mettre en œuvre A* de manière efficace.

Défis communs et techniques d'optimisation

Si A* est un outil puissant, sa mise en œuvre efficace nécessite de relever plusieurs défis communs. L'obstacle le plus important auquel les développeurs sont confrontés est la gestion efficace des ressources, en particulier lorsqu'il s'agit de grands espaces de recherche.

Les principaux défis sont les suivants :

• Consommation de mémoire dans les grands graphes
• Goulets d'étranglement des performances avec une heuristique complexe
• Gestion des situations de rupture d'égalité
• Équilibrer la précision et la vitesse de calcul

Heureusement, il existe plusieurs stratégies d'optimisation efficaces pour relever ces défis :

• Pour la gestion de la mémoire, concentrez-vous sur des structures de données
• Utiliser des tas binaires pour la liste ouverte au lieu de tableaux
• Mise en œuvre d'un tableau de hachage pour accélérer les recherches dans les listes fermées
• Clear as data des nœuds inutiles après le traitement

Lorsque les performances sont essentielles, pensez à ces améliorations de la vitesse :

• Simplifier les calculs heuristiques dans la mesure du possible
• Utiliser l'arithmétique des nombres entiers au lieu de l'arithmétique des nombres à virgule flottante
• Mise en œuvre d'une recherche de chemin hiérarchique pour les cartes de grande taille

Une approche particulièrement efficace pour les grands espaces est la recherche bilatérale, c'est-à-dire la recherche simultanée du point de départ et du point d'arrivée. En outre, lorsque vous travaillez avec un système de recherche de chemin basé sur une grille, vous pouvez améliorer considérablement les performances en calculant à l'avance des valeurs heuristiques ou en utilisant des tableaux de consultation.

N'oubliez pas de choisir les techniques d'optimisation en fonction de vos exigences et contraintes spécifiques. La clé est de trouver le bon équilibre entre l'utilisation de la mémoire et la vitesse de calcul pour votre application.

Conclusion

L'algorithme A* est un outil fondamental dans les problèmes de recherche de chemin et de traversée de graphe. À travers ce guide, nous avons vu ses concepts fondamentaux, mis en œuvre une solution pratique en Python et examiné ses diverses applications. La force de l'algorithme réside dans son équilibre entre précision et efficacité, ce qui le rend inestimable dans divers domaines, des jeux à la robotique.

Bien que la mise en œuvre de l'A* comporte des défis, les techniques d'optimisation que nous avons examinées peuvent vous aider à créer des solutions efficaces. Si vous développez des jeux, planifiez les trajectoires de robots ou résolvez des problèmes de routage, la compréhension de l'algorithme A* vous offre une approche puissante pour trouver des trajectoires optimales dans vos applications.

La construction d'algorithmes aussi sophistiqués nécessite des bases solides en matière de concepts de programmation Python et de bonnes pratiques. Vous souhaitez renforcer vos bases en Python et vous attaquer à des algorithmes plus avancés comme A* ? 

Faites passer vos compétences en programmation au niveau supérieur grâce à notre cours Cours Python intermédiaire pour développeurs où vous maîtriserez les fonctions personnalisées, explorerez les modules essentiels et créerez des applications sophistiquées.