Tutorial de análise de componentes principais no R

Introdução à análise de componentes principais (PCA)

Como cientista de dados no setor de varejo, imagine que você esteja tentando entender o que faz um cliente feliz a partir de um conjunto de dados que contém estas cinco características: despesa mensal, idade, sexo, frequência de compra e classificação do produto. Para analisar melhor e tirar conclusões práticas, precisamos entender o conjunto de dados ou, no mínimo, visualizá-lo. Os seres humanos não conseguem visualizar facilmente mais de três dimensões, portanto, visualizar dados de clientes com cinco características (dimensões) não é simples. É nesse ponto que entra a análise de componentes principais (PCA, na sigla em inglês). 

"Mas o que é análise de componentes principais?"

É uma abordagem estatística que pode ser usada para analisar dados de alta dimensão e capturar as informações mais importantes deles. Isso é feito transformando os dados originais em um espaço de menor dimensão e agrupando variáveis altamente correlacionadas. Em nosso cenário, o PCA escolheria três características, como despesa mensal, frequência de compra e classificação do produto. Isso pode facilitar a visualização e a compreensão dos dados.

Após este tutorial, você terá uma melhor compreensão da análise de componentes principais e de como aplicá-la a cenários reais usando o famoso pacote corrr no R.

Assista e saiba mais sobre a análise de componentes principais no R neste vídeo do nosso curso.

Como funciona o PCA? Um guia de cinco etapas

Embora nosso foco seja o PCA, vamos ter em mente as cinco principais técnicas de componentes principais a seguir, que visam resumir e visualizar dados multivariados. A PCA, ao contrário das outras técnicas, só funciona com variáveis quantitativas. 

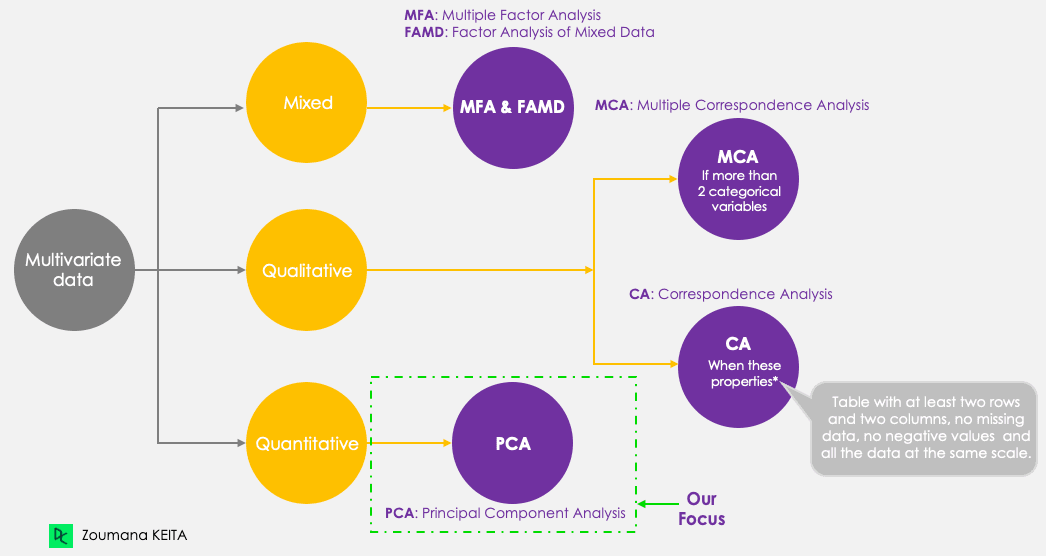
Métodos de componentes principais

Não entraremos na explicação do conceito matemático, que pode ser um tanto complexo.  Entretanto, a compreensão das cinco etapas a seguir pode dar uma ideia melhor de como calcular a PCA. 

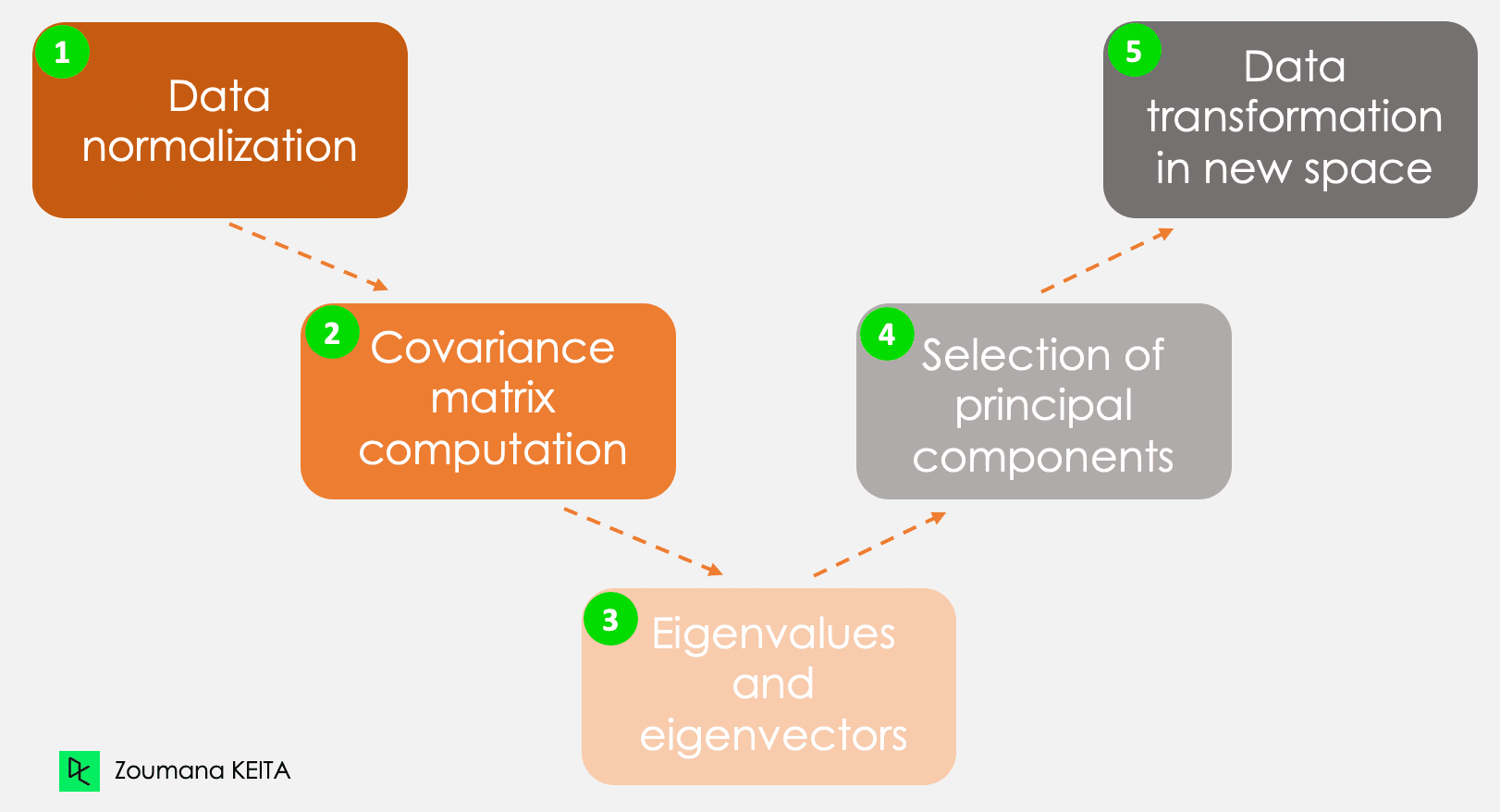
As cinco etapas principais para calcular os componentes principais

Etapa 1 - Normalização de dados

Considerando o exemplo da introdução, vamos considerar, por exemplo, as seguintes informações para um determinado cliente. 

• Despesas mensais: US$ 300
• Idade: 27
• Classificação: 4.5

Essas informações têm escalas diferentes e a execução da PCA usando esses dados levará a um resultado tendencioso. É nesse ponto que entra a normalização dos dados. Isso garante que cada atributo tenha o mesmo nível de contribuição, evitando que uma variável domine as outras. Para cada variável, a normalização é feita subtraindo sua média e dividindo pelo seu desvio padrão.   

Etapa 2 - Matriz de covariância

Como o próprio nome sugere, essa etapa consiste em calcular a matriz de covariáveis a partir dos dados normalizados. Essa é uma matriz simétrica, e cada elemento (i, j) corresponde à covariância entre as variáveis i e j.

Etapa 3 - Vetores e valores próprios

Geometricamente, um vetor próprio representa uma direção, como "vertical" ou "90 graus". Um valor próprio, por outro lado, é um número que representa a quantidade de variação presente nos dados para uma determinada direção. Cada vetor próprio tem seu valor próprio correspondente. 

Etapa 4 - Seleção dos componentes principais

Há tantos pares de vetores e valores próprios quanto o número de variáveis nos dados. Nos dados com apenas despesas mensais, idade e taxa, haverá três pares. Nem todos os pares são relevantes. Portanto, o vetor próprio com o maior valor próprio corresponde ao primeiro componente principal. O segundo componente principal é o vetor próprio com o segundo maior valor próprio, e assim por diante.

Etapa 5 - Transformação de dados em um novo espaço dimensional

Essa etapa envolve a reorientação dos dados originais em um novo subespaço definido pelos componentes principais. Essa reorientação é feita multiplicando-se os dados originais pelos vetores próprios calculados anteriormente.

É importante lembrar que essa transformação não modifica os dados originais em si, mas fornece uma nova perspectiva para representar melhor os dados. 

Aplicações da análise de componentes principais 

A análise de componentes principais tem várias aplicações em nosso dia a dia, incluindo (mas não se limitando a) finanças, processamento de imagens, saúde e segurança.

Finanças

A previsão de preços de ações com base em preços anteriores é uma noção usada em pesquisas há anos. A PCA pode ser usada para reduzir a dimensionalidade e analisar os dados para ajudar os especialistas a encontrar componentes relevantes que respondam pela maior parte da variabilidade dos dados. Você pode saber mais sobre a redução de dimensionalidade no R em nosso curso dedicado. 

Processamento de imagens

Uma imagem é composta de vários recursos. A PCA é aplicada principalmente na compressão de imagens para reter os detalhes essenciais de uma determinada imagem e, ao mesmo tempo, reduzir o número de dimensões. Além disso, a PCA pode ser usada para tarefas mais complicadas, como o reconhecimento de imagens.   

Assistência médica

Na mesma lógica da compressão de imagens. A PCA é usada em exames de ressonância magnética (MRI) para reduzir a dimensionalidade das imagens para melhorar a visualização e a análise médica. Ele também pode ser integrado a tecnologias médicas usadas, por exemplo, para reconhecer uma determinada doença a partir de exames de imagem.

Segurança

Os sistemas biométricos usados para o reconhecimento de impressões digitais podem integrar tecnologias que aproveitam a análise de componentes principais para extrair os recursos mais relevantes, como a textura da impressão digital e informações adicionais. 

Exemplo real de PCA em R

Agora que você entende a teoria subjacente do PCA, finalmente está pronto para vê-lo em ação.

Esta seção abrange todas as etapas, desde a instalação dos pacotes relevantes, o carregamento e a preparação dos dados, a aplicação da análise de componentes principais no R e a interpretação dos resultados. 

O código-fonte está disponível no espaço de trabalho da DataCamp.

Configuração do ambiente 

Para executar este tutorial com êxito, você precisará das seguintes bibliotecas, e cada uma delas requer duas etapas principais para ser usada com eficiência: 

• Instale a biblioteca para acessar todas as funções.
• Carregar para poder usar todas as funções.

pacote corrr no R

Este é um pacote R para análise de correlação. Ele se concentra principalmente na criação e no manuseio de quadros de dados R. Abaixo estão as etapas para instalar e carregar a biblioteca. 

install.packages("corrr")
library('corrr')

Pacote ggcorrplot no R

O pacote ggcorrplot fornece várias funções, mas não se limita à função ggplot2, que facilita a visualização da matriz de correlação. Da mesma forma que a instrução acima, a instalação é simples.

install.packages("ggcorrplot")
library(ggcorrplot)

Pacote FactoMineR em R

Usado principalmente para análise de dados exploratórios multivariados; o pacote factoMineR dá acesso ao módulo PCA para realizar a análise de componentes principais. 

install.packages("FactoMineR")
library("FactoMineR")

pacote factoextra no R

Esse último pacote fornece todas as funções relevantes para visualizar os resultados da análise de componentes principais. Essas funções incluem, entre outras, scree plot e biplot, apenas para mencionar duas das técnicas de visualização abordadas mais adiante no artigo.

Explorando os dados

Antes de carregar os dados e realizar qualquer exploração adicional, é bom entender e ter as informações básicas relacionadas aos dados com os quais você trabalhará.  

Dados de proteínas

O conjunto de dados de proteína é um conjunto de dados multivariados de valor real que descreve o consumo médio de proteína por cidadãos de 25 países europeus. 

Para cada país, há dez colunas. Os oito primeiros correspondem aos diferentes tipos de proteínas. O último corresponde ao valor total dos valores médios das proteínas.

Vamos ter uma visão geral rápida dos dados. 

Primeiro, carregamos os dados usando a função read.csv() e, em seguida, str(), que fornece a imagem abaixo. 

protein_data <- read.csv("protein.csv")
str(protein_data)

Podemos ver que o conjunto de dados tem 25 observações e 11 colunas, e cada variável é numérica, exceto a coluna Country, que é um texto. 

Descrição dos dados da proteína

Verificação de valores nulos 

A presença de valores ausentes pode distorcer o resultado da PCA. Portanto, é altamente recomendável realizar a abordagem adequada para lidar com esses valores.  Nosso tutorial Principais técnicas para lidar com valores ausentes que todo cientista de dados deve conhecer pode ajudá-lo a fazer a escolha certa. 

colSums(is.na(protein_data))

A função colSums() combinada com is.na() retorna o número de valores ausentes em cada coluna. Como podemos ver abaixo, nenhuma das colunas tem valores ausentes.

Número de valores ausentes em cada coluna

Normalização dos dados

Conforme declarado no início do artigo, a PCA só funciona com valores numéricos. Portanto, precisamos nos livrar da coluna Country. Além disso, a coluna Total não é relevante para a análise, pois é a combinação linear das variáveis numéricas restantes.

O código abaixo cria novos dados com apenas colunas numéricas.

numerical_data <- protein_data[,2:10]

head(numerical_data)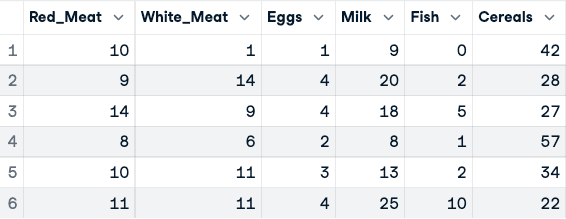

Antes da normalização dos dados (somente as cinco primeiras colunas são mostradas)

Agora, a normalização pode ser aplicada usando a função scale(). 

data_normalized <- scale(numerical_data)
head(data_normalized)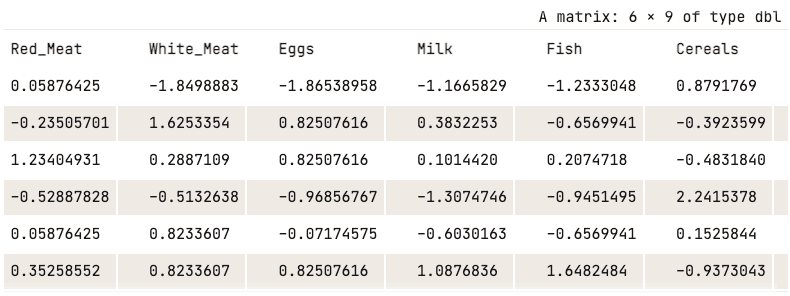

Dados normalizados (somente as cinco primeiras colunas são mostradas)

Calcular a matriz de correlação

Embora a matriz de covariância seja declarada nas cinco etapas anteriores, a correlação também pode ser usada e pode ser calculada usando a função cor() do pacote corrr. O site ggcorrplot() pode ser aplicado para melhor visualização.

corr_matrix <- cor(data_normalized)
ggcorrplot(corr_matrix)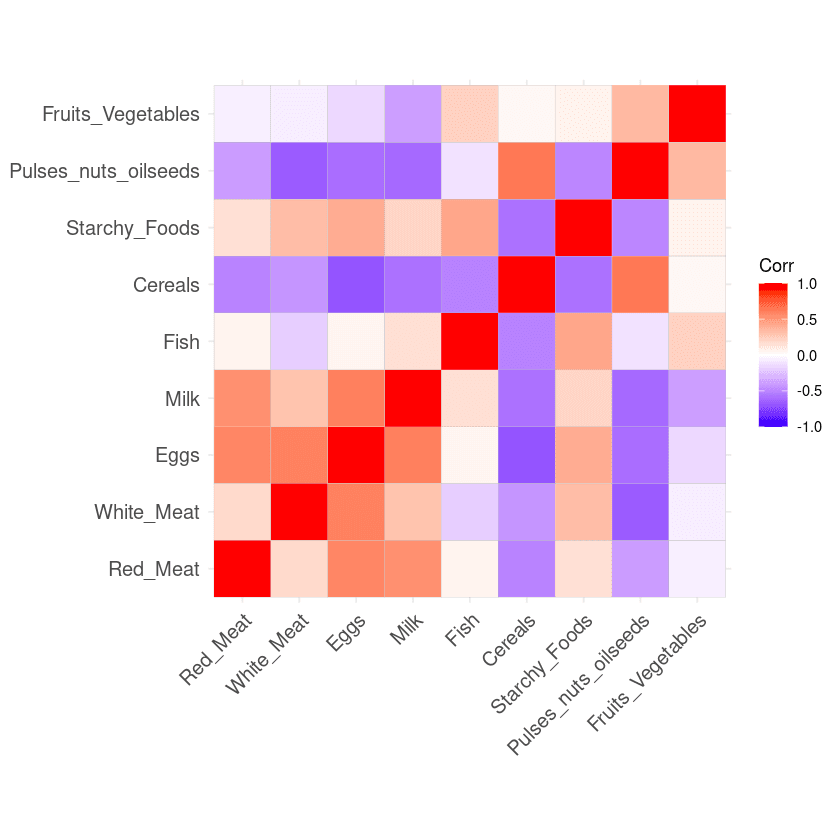

Matriz de correlação dos dados

O resultado da matriz de correlação pode ser interpretado da seguinte forma: 

• Quanto maior o valor, maior a correlação positiva entre as duas variáveis.
• Quanto mais próximo o valor de -1, mais negativamente correlacionados eles são.

Aplicação de PCA

Agora, todos os recursos estão disponíveis para realizar a análise PCA. Primeiro, o princomp() calcula o PCA, e a função summary() mostra o resultado.

data.pca <- princomp(corr_matrix)
summary(data.pca)

R Resumo do PCA 

Na captura de tela anterior, observamos que foram gerados nove componentes principais (Comp.1 a Comp.9), que também correspondem ao número de variáveis nos dados.

Cada componente explica uma porcentagem da variação total do conjunto de dados. Na seção Proporção cumulativa, o primeiro componente principal explica quase 77% da variação total. Isso implica que quase dois terços dos dados no conjunto de 9 variáveis podem ser representados apenas pelo primeiro componente principal. O segundo explica 12,08% da variação total. 

A proporção cumulativa de Comp.1 e Comp.2 explica quase 89% da variação total. Isso significa que os dois primeiros componentes principais podem representar os dados com precisão. 

É ótimo ter os dois primeiros componentes, mas o que eles realmente significam? 

Isso pode ser respondido explorando como eles se relacionam com cada coluna usando as cargas de cada componente principal. 

data.pca$loadings[, 1:2]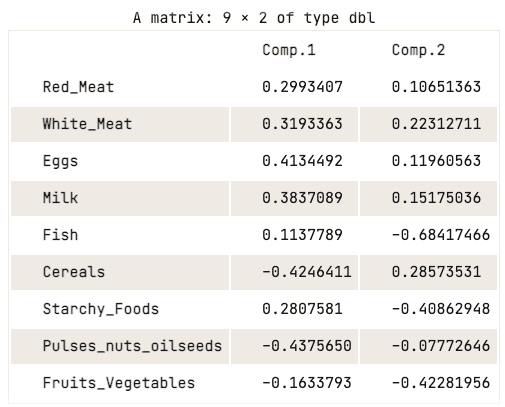

Matriz de carregamento dos dois primeiros componentes principais

A matriz de carga mostra que o primeiro componente principal tem valores positivos altos para carne vermelha, carne branca, ovos e leite. No entanto, os valores para cereais, leguminosas, nozes e sementes oleaginosas e frutas e legumes são relativamente negativos. Isso sugere que os países com maior ingestão de proteína animal estão em excesso, enquanto os países com menor ingestão estão em déficit.

Quando se trata do segundo componente principal, ele apresenta valores negativos elevados para peixes, alimentos ricos em amido e frutas e legumes.  Isso implica que as dietas dos países subjacentes são altamente influenciadas por sua localização, como regiões costeiras para peixes e regiões do interior para uma dieta rica em vegetais e batatas.

Visualização dos componentes principais 

A análise anterior da matriz de carga deu uma boa compreensão da relação entre cada um dos dois primeiros componentes principais e os atributos nos dados. No entanto, ele pode não ser visualmente atraente. 

Existem algumas estratégias de visualização padrão que podem ajudar o usuário a obter informações sobre os dados, e esta seção tem como objetivo abordar algumas dessas abordagens, começando com o gráfico scree.  

Gráfico Scree

A primeira abordagem da lista é o gráfico scree. Ele é usado para visualizar a importância de cada componente principal e pode ser usado para determinar o número de componentes principais a serem retidos. O gráfico scree pode ser gerado usando a função fviz_eig(). 

fviz_eig(data.pca, addlabels = TRUE)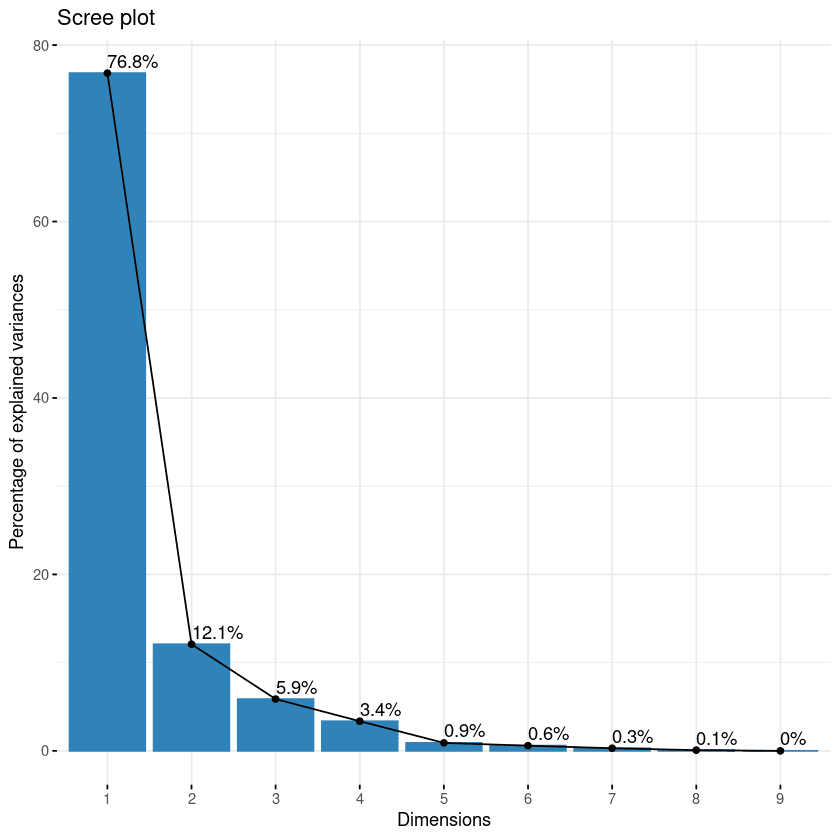

Gráfico Scree dos componentes

Esse gráfico mostra os valores próprios em uma curva descendente, do maior para o menor. Os dois primeiros componentes podem ser considerados os mais significativos, pois contêm quase 89% do total de informações dos dados.

Biplot dos atributos

Com o biplot, é possível visualizar as semelhanças e dissimilaridades entre as amostras, além de mostrar o impacto de cada atributo em cada um dos componentes principais.

# Graph of the variables
fviz_pca_var(data.pca, col.var = "black")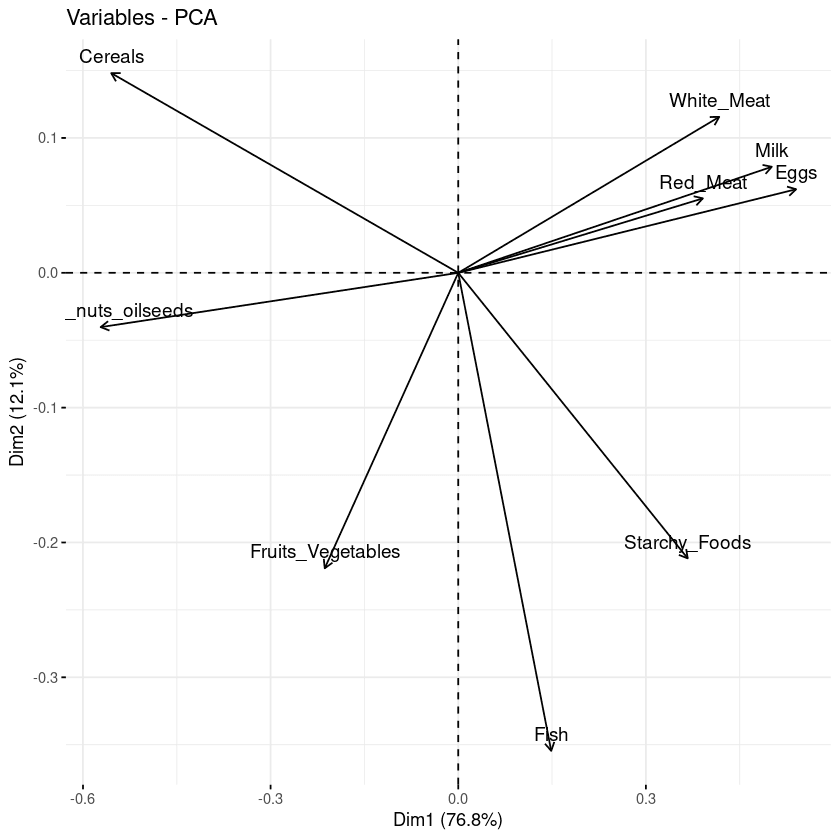

Biplot das variáveis com relação aos componentes principais

Três informações principais podem ser observadas no gráfico anterior. 

• Primeiro, todas as variáveis agrupadas estão positivamente correlacionadas entre si, e esse é o caso, por exemplo, da carne branca/vermelha, do leite e dos ovos, que têm uma correlação positiva entre si. Esse resultado é surpreendente porque eles têm os valores mais altos na matriz de carga com relação ao primeiro componente principal.
• Então, quanto maior for a distância entre a variável e a origem, melhor será a representação dessa variável. No biplot, ovos, leite e carne branca têm maior magnitude em comparação com a carne vermelha e, portanto, são bem representados em comparação com a carne vermelha.
• Por fim, as variáveis que estão negativamente correlacionadas são exibidas nos lados opostos da origem do biplot. 

Contribuição de cada variável 

O objetivo da terceira visualização é determinar o quanto cada variável é representada em um determinado componente. Essa qualidade de representação é chamada de Cos2 e corresponde ao cosseno quadrado, e é calculada usando a função fviz_cos2.

• Um valor baixo significa que a variável não é perfeitamente representada por esse componente. 
• Um valor alto, por outro lado, significa uma boa representação da variável nesse componente.

fviz_cos2(data.pca, choice = "var", axes = 1:2)

O código acima calculou o valor do cosseno quadrado para cada variável com relação aos dois primeiros componentes principais. 

Na ilustração abaixo, os cereais, as sementes oleaginosas, os ovos e o leite são as quatro principais variáveis com o maior cos2 e, portanto, as que mais contribuem para o PC1 e o PC2.

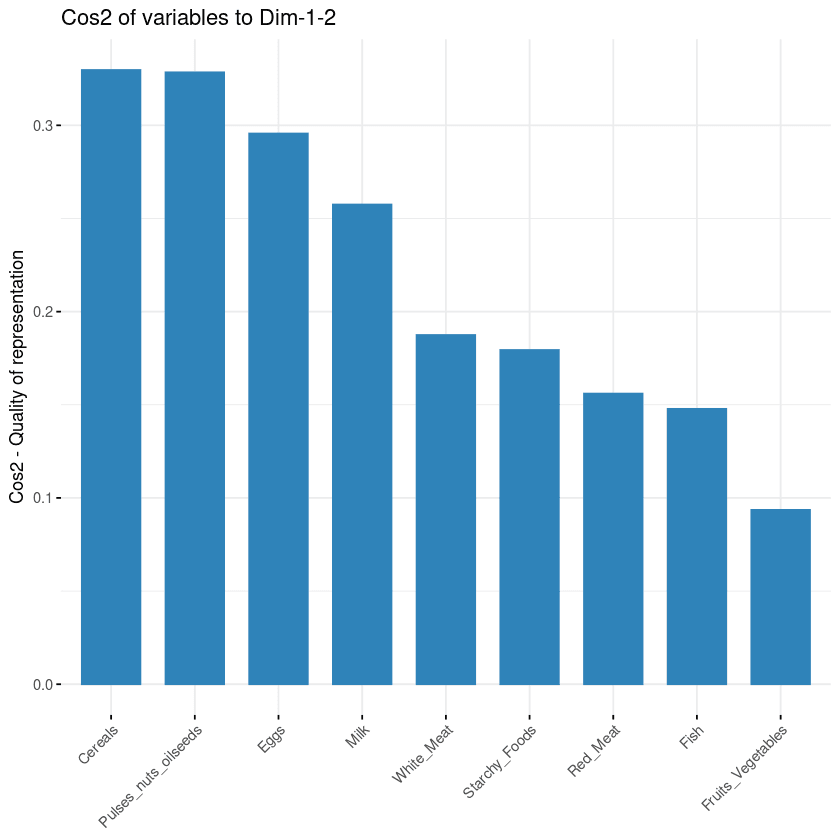
Contribuição das variáveis para os componentes principais

Biplot combinado com cos2 

As duas últimas abordagens de visualização: biplot e importância dos atributos podem ser combinadas para criar um único biplot, em que os atributos com pontuações cos2 semelhantes terão cores semelhantes.  Isso é obtido com o ajuste fino da função fviz_pca_var da seguinte forma:  

fviz_pca_var(data.pca, col.var = "cos2",
            gradient.cols = c("black", "orange", "green"),
            repel = TRUE)

No biplot abaixo:

• Os atributos de cos2 alto são coloridos em verde: Cereais, leguminosas, sementes oleaginosas, ovos e leite.  
• Os atributos cos2 médios têm uma cor laranja: carne branca, alimentos ricos em amido, peixe e carne vermelha.
• Por fim, os atributos de baixo cos2 têm uma cor preta: frutas e vegetais, 

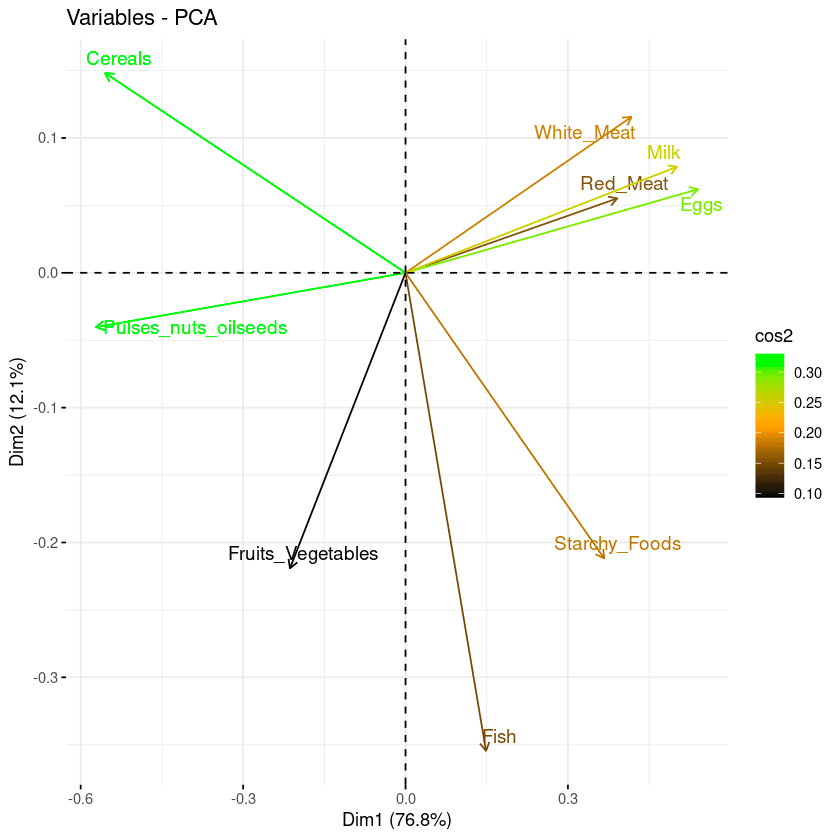
Combinação de biplot e cos2 score

Conclusão

Este artigo abordou o que é a análise de componentes principais e sua importância na análise de dados usando a matriz de correlação do pacote corrr. Além de abordar alguns aplicativos do mundo real, ele também o orientou em um exemplo de PCA com diferentes estratégias de visualização, desde o uso da função existente até o ajuste fino usando a combinação de biplot e cos2 para melhor compreensão e visualização da relação entre a análise pca em r e os atributos. 

Esperamos que ele forneça a você as habilidades relevantes para visualizar e entender com eficiência os insights ocultos dos seus dados.  

Para aprofundar seu aprendizado sobre a análise de componentes principais, considere o tutorial Análise de componentes principais em Python. Ele ilustrou o uso do PCA com Python em conjuntos de dados tabulares e de imagens. Nosso curso Introduction to R é uma boa próxima etapa para dominar os fundamentos da análise de dados em R, incluindo vetores, listas e quadros de dados, e praticar o uso do R com conjuntos de dados reais.