Introdução aos modelos lineares
Pratique Lasso e Ridge Regression em Python com este exercício prático.
A regressão linear é um tipo de modelo linear que é considerado o algoritmo preditivo mais básico e comumente usado. Isso não pode ser dissociado de sua arquitetura simples, porém eficaz. Um modelo linear pressupõe uma relação linear entre a(s) variável(is) de entrada 𝑥 e uma variável de saída y. A equação de um modelo linear tem a seguinte aparência:
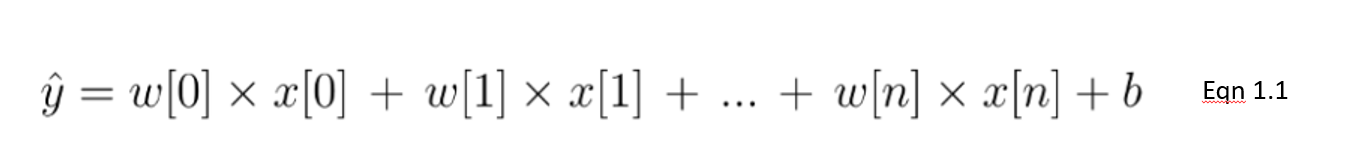
Nesta equação 1.1, mostramos um modelo linear com um número n de recursos. w é considerado o coeficiente (ou pesos) atribuído a cada recurso - um indicador de sua importância para o resultado y. Por exemplo, presumimos que a temperatura é um fator mais importante nas vendas de sorvete do que o fato de ser um feriado. O peso atribuído à temperatura em nosso modelo linear será maior do que a variável de feriado público.
O objetivo de um modelo linear passa a ser otimizar o peso (b) por meio da função de custo na equação 1.2. A função de custo calcula o erro entre as previsões e os valores reais, representado como um único número de valor real. A função de custo é o erro médio em n amostras do conjunto de dados, representado abaixo como:
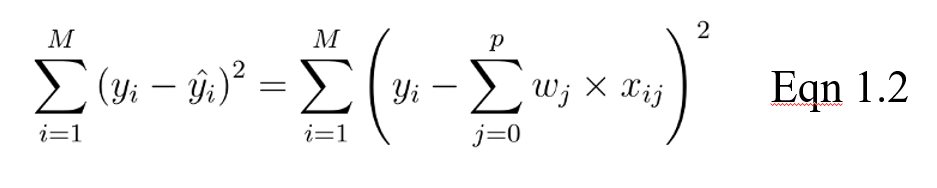
Na equação acima, yi é o valor real e esse é o valor previsto de nossa equação linear, em que M é o número de linhas e P é o número de recursos.
Regularização
Quando se trata de modelos de treinamento, há dois problemas principais que podem ser encontrados: overfitting e underfitting.
- O superajuste ocorre quando o modelo tem bom desempenho no conjunto de treinamento, mas não tão bom nos dados não vistos (teste).
- A subadaptação ocorre quando o desempenho não é bom nem no conjunto de treinamento nem no conjunto de teste.
Particularmente, a regularização é implementada para evitar o ajuste excessivo dos dados, especialmente quando há uma grande variação entre os desempenhos dos conjuntos de treinamento e teste. Com a regularização, o número de recursos usados no treinamento é mantido constante, mas a magnitude dos coeficientes (w), conforme visto na equação 1.1, é reduzida.
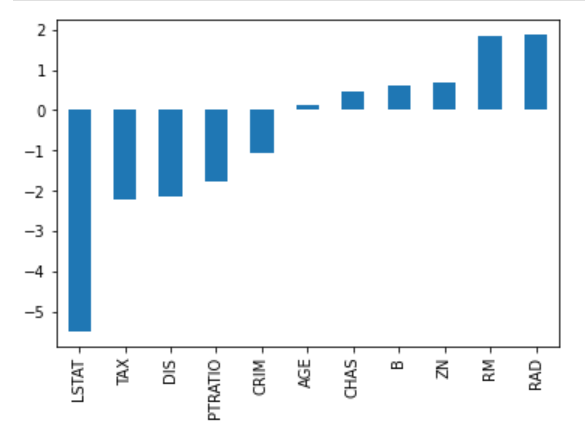
Considere a imagem de coeficientes abaixo para prever os preços dos imóveis. Embora haja um grande número de preditores, RM e RAD têm os maiores coeficientes. A implicação disso é que os preços das moradias serão impulsionados de forma mais significativa por esses dois recursos, levando a um ajuste excessivo, em que padrões generalizáveis não foram aprendidos.
Há diferentes maneiras de reduzir a complexidade do modelo e evitar o ajuste excessivo em modelos lineares. Isso inclui modelos de regressão ridge e lasso.
Introdução à regressão Lasso
Essa é uma técnica de regularização usada na seleção de recursos usando o método Shrinkage, também conhecido como método de regressão penalizada. Lasso é a abreviação de Least Absolute Shrinkageand Selection Operator (operadorde seleçãoe redução mínima absoluta), que é usado tanto para regularização quanto para seleção de modelos. Se um modelo usar a técnica de regularização L1, ele será chamado de regressão lasso.
Regressão Lasso para regularização
Nessa técnica de redução, os coeficientes determinados no modelo linear da equação 1.1. acima são reduzidos em direção ao ponto central como a média, introduzindo um fator de penalização chamado de valores alfa α (ou, às vezes, lamda).
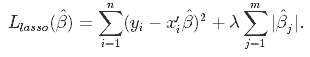
Alfa (α) é o termo de penalidade que denota a quantidade de redução (ou restrição) que será implementada na equação. Com alfa definido como zero, você verá que esse é o equivalente ao modelo de regressão linear da equação 1.2, e um valor maior penaliza a função de otimização. Portanto, a regressão com laço diminui os coeficientes e ajuda a reduzir a complexidade do modelo e a multicolinearidade.
Alfa (α) pode ser qualquer número de valor real entre zero e infinito; quanto maior o valor, mais agressiva é a penalização.
Regressão Lasso para seleção de modelos
Devido ao fato de que os coeficientes serão encolhidos em direção a uma média de zero, os recursos menos importantes em um conjunto de dados são eliminados quando penalizados. A redução desses coeficientes com base no valor alfa fornecido leva a alguma forma de seleção automática de recursos, pois as variáveis de entrada são removidas em uma abordagem eficaz.
Regressão Ridge
Semelhante à regressão lasso, a regressão ridge impõe uma restrição semelhante aos coeficientes, introduzindo um fator de penalidade. Entretanto, enquanto a regressão lasso considera a magnitude dos coeficientes, a regressão ridge considera o quadrado.
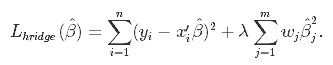
A regressão Ridge também é chamada de Regularização L2.
Por que o Lasso pode ser usado para a seleção de modelos, mas não para a regressão Ridge
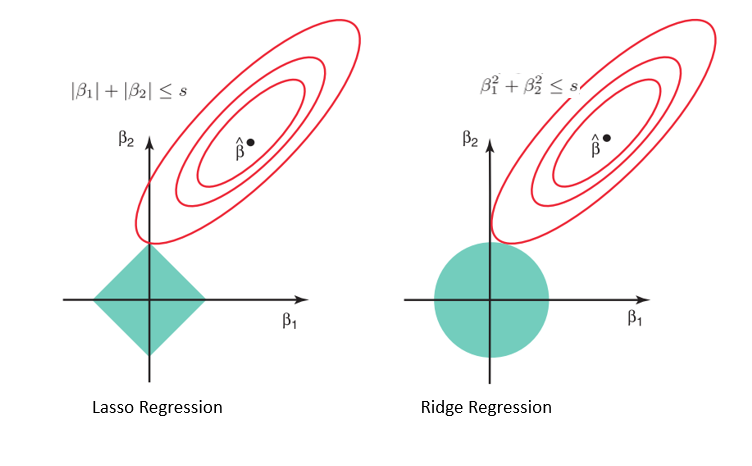
Considerando a geometria dos modelos de laço (esquerda) e de cumeeira (direita), os contornos elípticos (círculos vermelhos) são as funções de custo de cada um. O relaxamento das restrições introduzidas pelo fator de penalidade leva a um aumento na região restrita (diamante, círculo). Fazendo isso continuamente, chegaremos ao centro da elipse, onde os resultados dos modelos lasso e ridge são semelhantes aos de um modelo de regressão linear.
Entretanto, ambos os métodos determinam os coeficientes encontrando o primeiro ponto em que os contornos elípticos atingem a região de restrições. Como a regressão com laço assume uma forma de diamante no gráfico da região restrita, toda vez que as regiões elípticas se cruzam com esses cantos, pelo menos um dos coeficientes se torna zero. Isso é impossível no modelo de regressão de cumeeira, pois ele tem uma forma circular e, portanto, os valores podem ser reduzidos para perto de zero, mas nunca iguais a zero.
Implementação do Python
Para essa implementação, usaremos o conjunto de dados de moradias de Boston encontrado no Sklearn. O que pretendemos ver é:
- Como executar a regressão ridge e lasso em Python
- Compare os resultados com um modelo de regressão linear
Importação de dados e EDA
#libraries
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge, RidgeCV, Lasso
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston
#data
boston = load_boston()
boston_df=pd.DataFrame(boston.data,columns=boston.feature_names)
#target variable
boston_df['Price']=boston.target
#preview
boston_df.head()
#Exploration
plt.figure(figsize = (10, 10))
sns.heatmap(boston_df.corr(), annot = True)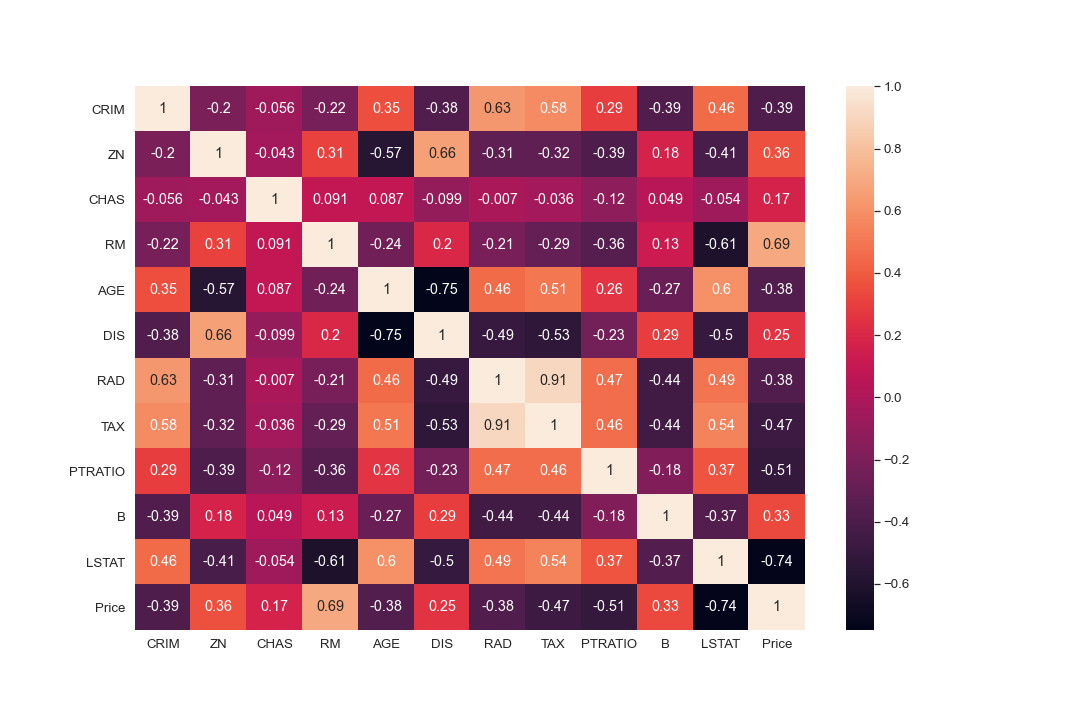
#There are cases of multicolinearity, we will drop a few columns
boston_df.drop(columns = ["INDUS", "NOX"], inplace = True)
#pairplot
sns.pairplot(boston_df)
#we will log the LSTAT Column
boston_df.LSTAT = np.log(boston_df.LSTAT)
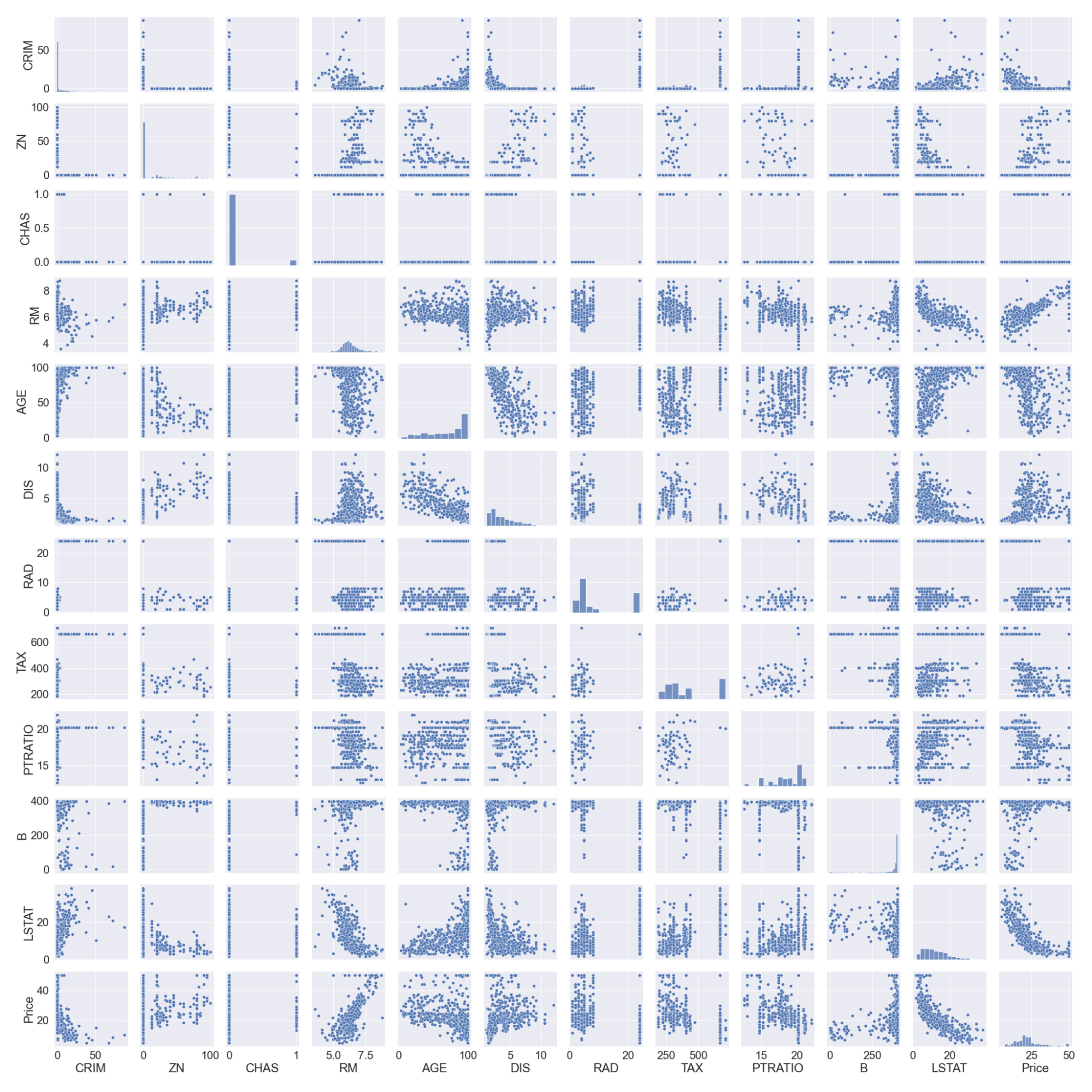
Observe que registramos a coluna LSTAT, pois ela não tem uma relação linear com a coluna de preço. Os modelos lineares pressupõem uma relação linear entre as variáveis x e y.
Divisão e dimensionamento de dados
#preview
features = boston_df.columns[0:11]
target = boston_df.columns[-1]
#X and y values
X = boston_df[features].values
y = boston_df[target].values
#splot
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=17)
print("The dimension of X_train is {}".format(X_train.shape))
print("The dimension of X_test is {}".format(X_test.shape))
#Scale features
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
Saída:

Modelos de regressão linear e de cumeeira
Criaremos um modelo de regressão linear e um modelo de regressão de cumeeira e, em seguida, compararemos os coeficientes em um gráfico. A pontuação dos conjuntos de treinamento e teste também nos ajudará a avaliar o desempenho do modelo.
#Model
lr = LinearRegression()
#Fit model
lr.fit(X_train, y_train)
#predict
#prediction = lr.predict(X_test)
#actual
actual = y_test
train_score_lr = lr.score(X_train, y_train)
test_score_lr = lr.score(X_test, y_test)
print("The train score for lr model is {}".format(train_score_lr))
print("The test score for lr model is {}".format(test_score_lr))
#Ridge Regression Model
ridgeReg = Ridge(alpha=10)
ridgeReg.fit(X_train,y_train)
#train and test scorefor ridge regression
train_score_ridge = ridgeReg.score(X_train, y_train)
test_score_ridge = ridgeReg.score(X_test, y_test)
print("\nRidge Model............................................\n")
print("The train score for ridge model is {}".format(train_score_ridge))
print("The test score for ridge model is {}".format(test_score_ridge))

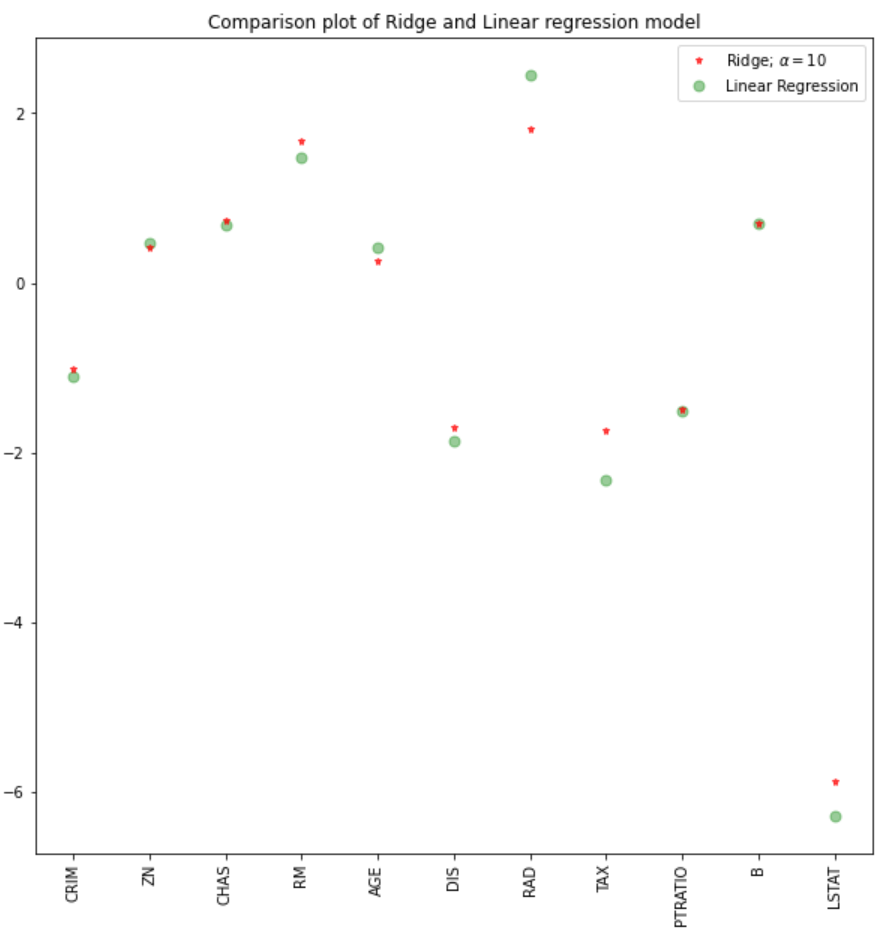
Usando um valor alfa de 10, a avaliação do modelo, o treinamento e os dados de teste indicam melhor desempenho no modelo de cumeeira do que no modelo de regressão linear.
Também podemos plotar os coeficientes para os modelos linear e de cumeeira.
plt.figure(figsize = (10, 10))
plt.plot(features,ridgeReg.coef_,alpha=0.7,linestyle='none',marker='*',markersize=5,color='red',label=r'Ridge; $\alpha = 10$',zorder=7)
#plt.plot(rr100.coef_,alpha=0.5,linestyle='none',marker='d',markersize=6,color='blue',label=r'Ridge; $\alpha = 100$')
plt.plot(features,lr.coef_,alpha=0.4,linestyle='none',marker='o',markersize=7,color='green',label='Linear Regression')
plt.xticks(rotation = 90)
plt.legend()
plt.show()
Regressão Lasso
#Lasso regression model
print("\nLasso Model............................................\n")
lasso = Lasso(alpha = 10)
lasso.fit(X_train,y_train)
train_score_ls =lasso.score(X_train,y_train)
test_score_ls =lasso.score(X_test,y_test)
print("The train score for ls model is {}".format(train_score_ls))
print("The test score for ls model is {}".format(test_score_ls))

Também podemos visualizar os coeficientes.
pd.Series(lasso.coef_, features).sort_values(ascending = True).plot(kind = "bar")
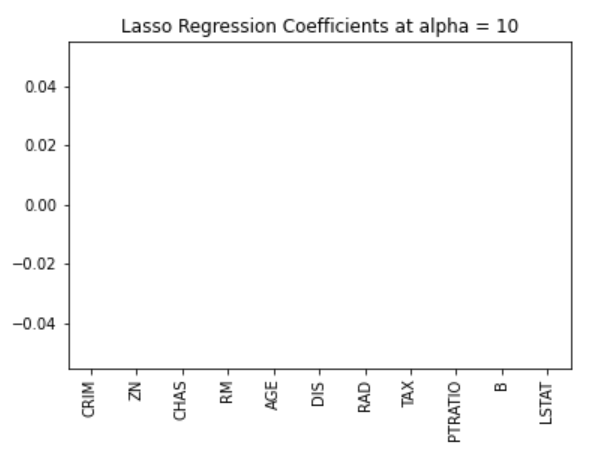
Anteriormente, estabelecemos que o modelo de laço pode ser inerte a zero devido ao formato de diamante da região de restrição. Nesse caso, o uso de um valor alfa de 10 penaliza demais o modelo e reduz todos os valores a zero. Podemos ver isso efetivamente visualizando os coeficientes do modelo, conforme mostrado na figura acima.
Seleção de valores alfa ideais usando validação cruzada no Sklearn
Talvez seja necessário experimentar diferentes valores de alfa para encontrar o valor ideal de restrição. Para esse caso, podemos usar o modelo de validação cruzada no pacote sklearn. Isso testará diferentes combinações de valores alfa e, em seguida, escolherá o melhor modelo.
#Using the linear CV model
from sklearn.linear_model import LassoCV
#Lasso Cross validation
lasso_cv = LassoCV(alphas = [0.0001, 0.001,0.01, 0.1, 1, 10], random_state=0).fit(X_train, y_train)
#score
print(lasso_cv.score(X_train, y_train))
print(lasso_cv.score(X_test, y_test))
Saída:

O modelo será treinado em diferentes valores alfa que eu especifiquei na função LassoCV. Podemos observar um melhor desempenho do modelo, eliminando o esforço tedioso de alterar manualmente os valores de alfa.
Podemos comparar os coeficientes do modelo lasso com os demais modelos (linear e ridge).
#plot size
plt.figure(figsize = (10, 10))
#add plot for ridge regression
plt.plot(features,ridgeReg.coef_,alpha=0.7,linestyle='none',marker='*',markersize=5,color='red',label=r'Ridge; $\alpha = 10$',zorder=7)
#add plot for lasso regression
plt.plot(lasso_cv.coef_,alpha=0.5,linestyle='none',marker='d',markersize=6,color='blue',label=r'lasso; $\alpha = grid$')
#add plot for linear model
plt.plot(features,lr.coef_,alpha=0.4,linestyle='none',marker='o',markersize=7,color='green',label='Linear Regression')
#rotate axis
plt.xticks(rotation = 90)
plt.legend()
plt.title("Comparison plot of Ridge, Lasso and Linear regression model")
plt.show()
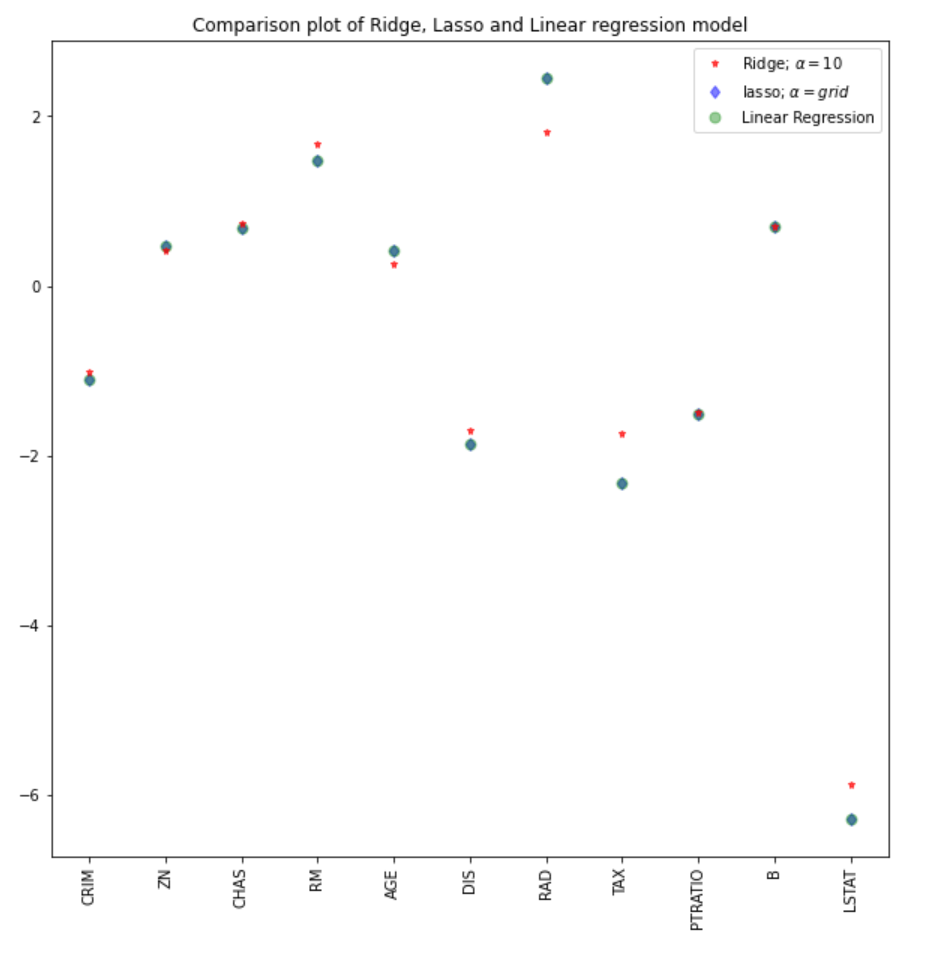
Observação: Uma abordagem semelhante poderia ser empregada para o modelo de regressão de cumeeira, o que poderia levar a melhores resultados. No pacote sklearn, a função RidgeCV tem desempenho semelhante.
#Using the linear CV model from sklearn.linear_model import RidgeCV #Lasso Cross validation ridge_cv = RidgeCV(alphas = [0.0001, 0.001,0.01, 0.1, 1, 10]).fit(X_train, y_train) #score print("The train score for ridge model is {}".format(ridge_cv.score(X_train, y_train))) print("The train score for ridge model is {}".format(ridge_cv.score(X_test, y_test)))
Aprenda sobre outros tipos de regressão com nossos tutoriais de regressão logística em python e regressão linear em python.
Conclusão
Vimos uma implementação de modelos de regressão ridge e lasso e os conceitos teóricos e matemáticos por trás dessas técnicas. Algumas das principais conclusões desse tutorial incluem:
- A função de custo da regressão ridge e da regressão lasso é semelhante. No entanto, a regressão de cumeeira considera o quadrado dos coeficientes e o laço considera a magnitude.
- A regressão Lasso pode ser usada para a seleção automática de recursos, pois a geometria de sua região restrita permite que os valores do coeficiente sejam inertes a zero.
- Um valor alfa de zero no modelo ridge ou lasso terá resultados semelhantes aos do modelo de regressão.
- Quanto maior o valor alfa, mais agressiva é a penalização.
Você pode encontrar um notebook mais robusto e completo para a implementação em python aqui, ou mergulhar fundo nas regressões com nosso curso Introduction to Regression in Python.

