Perceptrons multicamadas em aprendizado de máquina: Um guia abrangente

Uma rede neural artificial (RNA) é um modelo de aprendizado de máquina inspirado na estrutura e na função da rede interconectada de neurônios do cérebro humano. Ele consiste em nós interconectados chamados neurônios artificiais, organizados em camadas. As informações fluem pela rede, com cada neurônio processando sinais de entrada e produzindo um sinal de saída que influencia outros neurônios da rede.

Um perceptron multicamada (MLP) é um tipo de rede neural artificial que consiste em várias camadas de neurônios. Os neurônios do MLP normalmente usam funções de ativação não lineares, permitindo que a rede aprenda padrões complexos nos dados. Os MLPs são importantes no aprendizado de máquina porque podem aprender relações não lineares nos dados, o que os torna modelos poderosos para tarefas como classificação, regressão e reconhecimento de padrões. Neste tutorial, vamos nos aprofundar nos conceitos básicos do MLP e entender seu funcionamento interno.

Noções básicas de redes neurais

As redes neurais ou redes neurais artificiais são ferramentas fundamentais para o aprendizado de máquina, impulsionando muitos algoritmos e aplicativos de última geração em vários domínios, incluindo visão computacional, processamento de linguagem natural, robótica e muito mais.

Uma rede neural consiste em nós interconectados, chamados neurônios, organizados em camadas. Cada neurônio recebe sinais de entrada, executa um cálculo sobre eles usando uma função de ativação e produz um sinal de saída que pode ser transmitido a outros neurônios da rede. Uma função de ativação determina a saída de um neurônio com base em sua entrada. Essas funções introduzem a não linearidade na rede, permitindo que ela aprenda padrões complexos nos dados.

Em geral, a rede é organizada em camadas, começando pela camada de entrada, na qual os dados são introduzidos. Em seguida, há as camadas ocultas, onde são realizados os cálculos e, por fim, a camada de saída, onde são feitas as previsões ou tomadas as decisões.

Os neurônios das camadas adjacentes são conectados por conexões ponderadas, que transmitem sinais de uma camada para a outra. A força dessas conexões, representada pelos pesos, determina o grau de influência que a saída de um neurônio tem sobre a entrada de outro neurônio. Durante o processo de treinamento, a rede aprende a ajustar seus pesos com base em exemplos fornecidos em um conjunto de dados de treinamento. Além disso, cada neurônio normalmente tem um viés associado, o que permite que o neurônio ajuste seu limite de saída.

As redes neurais são treinadas usando técnicas chamadas de propagação feedforward e backpropagation. Durante a propagação feedforward, os dados de entrada são passados pela rede camada por camada, com cada camada realizando um cálculo com base nas entradas que recebe e passando o resultado para a próxima camada.

O backpropagation é um algoritmo usado para treinar redes neurais, ajustando iterativamente os pesos e as tendências da rede para minimizar a função de perda. Uma função de perda (também conhecida como função de custo ou função objetivo) é uma medida de quão bem as previsões do modelo correspondem aos valores-alvo reais nos dados de treinamento. A função de perda quantifica a diferença entre a saída prevista do modelo e a saída real, fornecendo um sinal que orienta o processo de otimização durante o treinamento.

O objetivo do treinamento de uma rede neural é minimizar essa função de perda ajustando os pesos e as tendências. Os ajustes são orientados por um algoritmo de otimização, como a descida de gradiente. Vamos revisar alguns desses tópicos com mais detalhes mais adiante neste tutorial.

Tipos de redes neurais

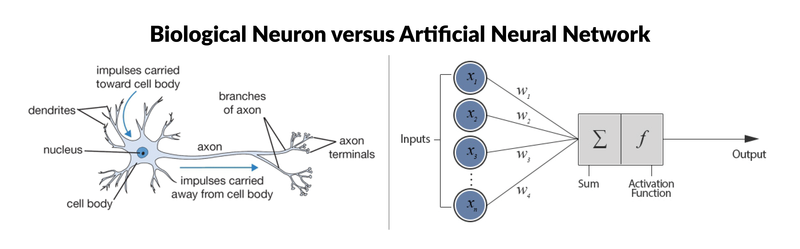
Crédito da imagem: Tutorial do Keras: Aprendizagem profunda em Python

A RNA mostrada à direita da imagem é uma rede neural simples chamada "perceptron". Ele consiste em uma única camada, que é a camada de entrada, com vários neurônios com seus próprios pesos; não há camadas ocultas. O algoritmo perceptron aprende os pesos para os sinais de entrada a fim de traçar um limite de decisão linear.

No entanto, para resolver problemas mais complicados e não lineares relacionados a tarefas de processamento de imagens, visão computacional e processamento de linguagem natural, trabalhamos com redes neurais profundas.

Confira o tutorial Introdução às redes neurais profundas da Datacamp para saber mais sobre redes neurais profundas e como construir uma do zero utilizando o TensorFlow e o Keras em Python. Se, em vez disso, você preferir usar a linguagem R, o Building Neural Network (NN) Models in R da Datacamp é a solução.

Há vários tipos de RNA, cada um projetado para tarefas e requisitos arquitetônicos específicos. Vamos discutir brevemente alguns dos tipos mais comuns antes de nos aprofundarmos nas MLPs.

Redes neurais feedforward (FNN)

Essa é a forma mais simples de RNAs, em que as informações fluem em uma única direção, da entrada para a saída. Não há ciclos ou loops na arquitetura da rede. Os perceptrons multicamadas (MLP) são um tipo de rede neural feedforward.

Redes neurais recorrentes (RNN)

Nos RNNs, as conexões entre os nós formam ciclos direcionados, permitindo que as informações persistam ao longo do tempo. Isso os torna adequados para tarefas que envolvem dados sequenciais, como previsão de séries temporais, processamento de linguagem natural e reconhecimento de fala.

Redes neurais convolucionais (CNN)

As CNNs são projetadas para processar com eficiência dados em forma de grade, como imagens. Eles consistem em camadas de filtros convolucionais que aprendem representações hierárquicas de recursos dentro dos dados de entrada. As CNNs são amplamente usadas em tarefas como classificação de imagens, detecção de objetos e segmentação de imagens.

Redes de memória longa de curto prazo (LSTM) e unidades recorrentes controladas (GRU)

Esses são tipos especializados de redes neurais recorrentes projetadas para resolver o problema do gradiente de desaparecimento na RNN tradicional. Os LSTMs e as GRUs incorporam mecanismos de gated para capturar melhor as dependências de longo alcance em dados sequenciais, o que os torna particularmente eficazes para tarefas como reconhecimento de fala, tradução automática e análise de sentimentos.

Autocodificador

Ele foi projetado para aprendizado não supervisionado e consiste em uma rede codificadora que comprime os dados de entrada em um espaço latente de dimensão inferior e uma rede decodificadora que reconstrói a entrada original a partir da representação latente. Os autoencodificadores são frequentemente usados para redução de dimensionalidade, redução de ruído de dados e modelagem generativa.

Redes Adversariais Generativas (GAN)

As GANs consistem em duas redes neurais, um gerador e um discriminador, treinadas simultaneamente em um ambiente competitivo. O gerador aprende a gerar amostras de dados sintéticos que não se distinguem dos dados reais, enquanto o discriminador aprende a distinguir entre amostras reais e falsas. Os GANs têm sido amplamente usados para gerar imagens, vídeos e outros tipos de dados realistas.

Perceptrons multicamadas

Um perceptron multicamadas é um tipo de rede neural feedforward que consiste em neurônios totalmente conectados com um tipo não linear de função de ativação. Ele é amplamente usado para distinguir dados que não são linearmente separáveis.

Os MLPs têm sido amplamente usados em vários campos, incluindo reconhecimento de imagens, processamento de linguagem natural e reconhecimento de fala, entre outros. Sua flexibilidade na arquitetura e a capacidade de aproximar qualquer função sob determinadas condições fazem deles um bloco de construção fundamental na pesquisa de aprendizagem profunda e redes neurais. Vamos nos aprofundar em alguns de seus principais conceitos.

Camada de entrada

A camada de entrada consiste em nós ou neurônios que recebem os dados de entrada iniciais. Cada neurônio representa um recurso ou uma dimensão dos dados de entrada. O número de neurônios na camada de entrada é determinado pela dimensionalidade dos dados de entrada.

Camada oculta

Entre as camadas de entrada e saída, pode haver uma ou mais camadas de neurônios. Cada neurônio em uma camada oculta recebe entradas de todos os neurônios da camada anterior (seja a camada de entrada ou outra camada oculta) e produz uma saída que é passada para a próxima camada. O número de camadas ocultas e o número de neurônios em cada camada oculta são hiperparâmetros que precisam ser determinados durante a fase de projeto do modelo.

Camada de saída

Essa camada consiste em neurônios que produzem a saída final da rede. O número de neurônios na camada de saída depende da natureza da tarefa. Na classificação binária, pode haver um ou dois neurônios, dependendo da função de ativação e representando a probabilidade de pertencer a uma classe; já nas tarefas de classificação multiclasse, pode haver vários neurônios na camada de saída.

Pesos

Os neurônios das camadas adjacentes estão totalmente conectados uns aos outros. Cada conexão tem um peso associado, que determina a força da conexão. Esses pesos são aprendidos durante o processo de treinamento.

Bias Neurons

Além dos neurônios de entrada e ocultos, cada camada (exceto a camada de entrada) geralmente inclui um neurônio de polarização que fornece uma entrada constante para os neurônios da próxima camada. O neurônio de polarização tem seu próprio peso associado a cada conexão, que também é aprendido durante o treinamento.

O neurônio de polarização muda efetivamente a função de ativação dos neurônios na camada subsequente, permitindo que a rede aprenda uma compensação ou polarização no limite de decisão. Ao ajustar os pesos conectados ao neurônio de polarização, o MLP pode aprender a controlar o limite de ativação e a se ajustar melhor aos dados de treinamento.

Observação: É importante observar que, no contexto das MLPs, bias pode se referir a dois conceitos relacionados, mas distintos: viés como um termo geral no aprendizado de máquina e o neurônio de viés (definido acima). No aprendizado de máquina geral, a tendência refere-se ao erro introduzido pela aproximação de um problema do mundo real com um modelo simplificado. O viés mede a capacidade do modelo de capturar os padrões subjacentes nos dados. Um viés alto indica que o modelo é muito simplista e pode não se ajustar aos dados, enquanto um viés baixo sugere que o modelo está capturando bem os padrões subjacentes.

Função de ativação

Normalmente, cada neurônio nas camadas ocultas e na camada de saída aplica uma função de ativação à sua soma ponderada de entradas. As funções de ativação comuns incluem sigmoide, tanh, ReLU (Unidade Linear Retificada) e softmax. Essas funções introduzem a não linearidade na rede, permitindo que ela aprenda padrões complexos nos dados.

Treinamento com retropropagação

Os MLPs são treinados usando o algoritmo de retropropagação, que calcula os gradientes de uma função de perda com relação aos parâmetros do modelo e atualiza os parâmetros iterativamente para minimizar a perda.

Funcionamento de um Perceptron de múltiplas camadas: Camada por camada

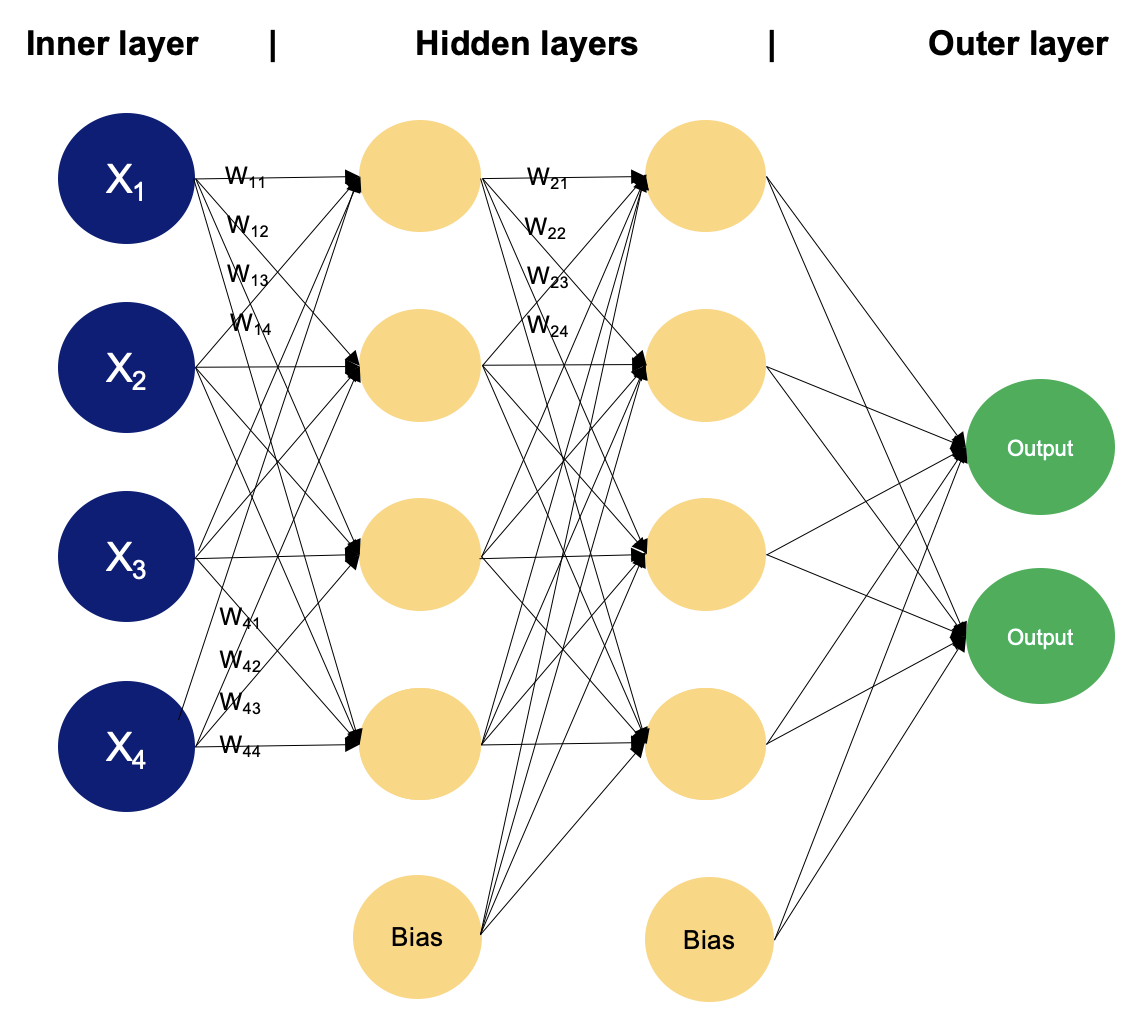
Exemplo de um MLP com duas camadas ocultas

Em um perceptron de múltiplas camadas, os neurônios processam as informações passo a passo, realizando cálculos que envolvem somas ponderadas e transformações não lineares. Vamos caminhar camada por camada para ver a mágica que existe dentro dela.

Camada de entrada

• A camada de entrada de um MLP recebe dados de entrada, que podem ser recursos extraídos das amostras de entrada em um conjunto de dados. Cada neurônio na camada de entrada representa um recurso.

• Os neurônios da camada de entrada não realizam nenhum cálculo; eles simplesmente passam os valores de entrada para os neurônios da primeira camada oculta.

Camadas ocultas

• As camadas ocultas de um MLP consistem em neurônios interconectados que realizam cálculos nos dados de entrada.

• Cada neurônio em uma camada oculta recebe entrada de todos os neurônios da camada anterior. As entradas são multiplicadas pelos pesos correspondentes, denotados como w. Os pesos determinam o grau de influência que a entrada de um neurônio tem sobre a saída de outro.

• Além dos pesos, cada neurônio na camada oculta tem um viés associado, denotado como b. A polarização fornece uma entrada adicional ao neurônio, permitindo que ele ajuste seu limite de saída. Assim como os pesos, as tendências são aprendidas durante o treinamento.
• Para cada neurônio em uma camada oculta ou na camada de saída, é calculada a soma ponderada de suas entradas. Isso envolve a multiplicação de cada entrada por seu peso correspondente, a soma desses produtos e a adição da polarização:

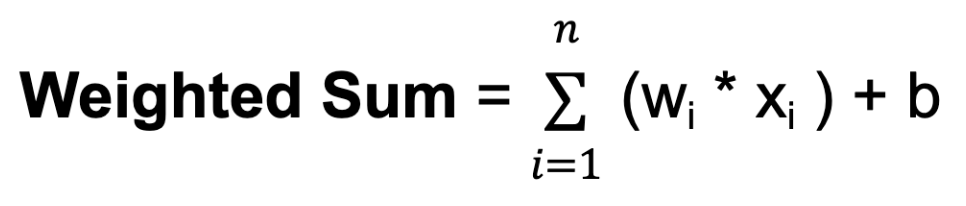
Em que n é o número total de conexões de entrada, wi é o peso da i-ésima entrada e xi é o i-ésimo valor de entrada.

• A soma ponderada é então passada por uma função de ativação, denotada como f. A função de ativação introduz a não linearidade na rede, permitindo que ela aprenda e represente relações complexas nos dados. A função de ativação determina o intervalo de saída do neurônio e seu comportamento em resposta a diferentes valores de entrada. A escolha da função de ativação depende da natureza da tarefa e das propriedades desejadas da rede.

Camada de saída

• A camada de saída de um MLP produz as previsões finais ou os resultados da rede. O número de neurônios na camada de saída depende da tarefa que está sendo executada (por exemplo, classificação binária, classificação multiclasse, regressão).

• Cada neurônio na camada de saída recebe entrada dos neurônios na última camada oculta e aplica uma função de ativação. Essa função de ativação geralmente é diferente das usadas nas camadas ocultas e produz o valor final de saída ou a previsão.

Durante o processo de treinamento, a rede aprende a ajustar os pesos associados às entradas de cada neurônio para minimizar a discrepância entre as saídas previstas e os valores-alvo reais nos dados de treinamento. Ajustando os pesos e aprendendo as funções de ativação apropriadas, a rede aprende a aproximar padrões e relacionamentos complexos nos dados, o que lhe permite fazer previsões precisas sobre amostras novas e não vistas.

Esse ajuste é orientado por um algoritmo de otimização, como o stochastic gradient descent (SGD), que calcula os gradientes de uma função de perda com relação aos pesos e atualiza os pesos iterativamente.

Vamos dar uma olhada mais de perto em como o SGD funciona.

Descida de Gradiente Estocástico (SGD)

1. Inicialização: O SGD começa com um conjunto inicial de parâmetros do modelo (pesos e vieses) de forma aleatória ou usando algum método predefinido.

2. Otimização iterativa: O objetivo dessa etapa é encontrar o mínimo de uma função de perda, movendo-se iterativamente na direção da diminuição mais acentuada do valor da função.

Para cada iteração (ou época) de treinamento:

• Embaralhe os dados de treinamento para garantir que o modelo não aprenda com os mesmos padrões na mesma ordem todas as vezes.
• Dividir os dados de treinamento em minilotes (pequenos subconjuntos de dados).
• Para cada mini-lote:
• Calcule o gradiente da função de perda com relação aos parâmetros do modelo usando apenas os pontos de dados no minilote. Essa estimativa de gradiente é uma aproximação estocástica do gradiente verdadeiro.
• Atualize os parâmetros do modelo dando um passo na direção oposta do gradiente, dimensionado por uma taxa de aprendizado:
  Θt+1 = θt - n * ⛛ J (θt)
  Onde:
  θt representa os parâmetros do modelo na iteração t. Esse parâmetro pode ser o peso
  ⛛ J (θt) é o gradiente da função de perda J em relação aos parâmetros θt
n é a taxa de aprendizado, que controla o tamanho das etapas realizadas durante a otimização

3. Direção de descida: O gradiente da função de perda indica a direção da subida mais íngreme. Para minimizar a função de perda, a descida do gradiente se move na direção oposta, em direção à descida mais íngreme.

4. Taxa de aprendizado: O tamanho da etapa adotada em cada iteração de descida de gradiente é determinado por um parâmetro chamado taxa de aprendizado, denotado acima como n. Esse parâmetro controla o tamanho das etapas realizadas em direção ao mínimo. Se a taxa de aprendizado for muito pequena, a convergência poderá ser lenta; se for muito grande, o algoritmo poderá oscilar ou divergir.

5. Convergência: Repita o processo por um número fixo de iterações ou até que um critério de convergência seja atendido (por exemplo, a alteração na função de perda está abaixo de um determinado limite).

O gradiente descendente estocástico atualiza os parâmetros do modelo com mais frequência usando subconjuntos menores de dados, o que o torna computacionalmente eficiente, especialmente para grandes conjuntos de dados. A aleatoriedade introduzida pelo SGD pode ter um efeito de regularização, evitando que o modelo se ajuste excessivamente aos dados de treinamento. Ele também é adequado para cenários de aprendizado on-line em que novos dados são disponibilizados de forma incremental, pois pode atualizar o modelo rapidamente com cada novo ponto de dados ou minilote.

No entanto, o SGD também pode apresentar alguns desafios, como o aumento do ruído devido à natureza estocástica da estimativa do gradiente e a necessidade de ajustar os hiperparâmetros, como a taxa de aprendizado. Várias extensões e adaptações do SGD, como a descida de gradiente estocástico em mini-lote, momentum e métodos de taxa de aprendizado adaptável, como AdaGrad, RMSProp e Adam, foram desenvolvidas para enfrentar esses desafios e melhorar a convergência e o desempenho.

Você viu o funcionamento das camadas do perceptron multicamadas e aprendeu sobre a descida de gradiente estocástica; para completar, há um último tópico a ser abordado: backpropagation.

Retropropagação

Backpropagation é a abreviação de "backward propagation of errors" (propagação retroativa de erros). No contexto da retropropagação, o SGD envolve a atualização dos parâmetros da rede de forma iterativa com base nos gradientes calculados durante cada lote de dados de treinamento. Em vez de calcular os gradientes usando todo o conjunto de dados de treinamento (que pode ser computacionalmente caro para conjuntos de dados grandes), o SGD calcula os gradientes usando pequenos subconjuntos aleatórios dos dados chamados de minilotes. Esta é uma visão geral de como funciona o algoritmo de retropropagação:

1. Passe para frente: Durante a passagem direta, os dados de entrada são alimentados na rede neural, e a saída da rede é calculada camada por camada. Cada neurônio calcula uma soma ponderada de suas entradas, aplica uma função de ativação ao resultado e passa a saída para os neurônios da próxima camada.

2. Cálculo de perdas: Após a passagem direta, a saída da rede é comparada com os valores-alvo reais, e uma função de perda é calculada para medir a discrepância entre a saída prevista e a saída real.

3. Passagem para trás (cálculo de gradiente): Na passagem para trás, os gradientes da função de perda com relação aos parâmetros da rede (pesos e polarizações) são calculados usando a regra da cadeia de cálculo. Os gradientes representam a taxa de alteração da função de perda com relação a cada parâmetro e fornecem informações sobre como ajustar os parâmetros para diminuir a perda.

4. Atualização de parâmetros: Depois que os gradientes são calculados, os parâmetros da rede são atualizados na direção oposta dos gradientes para minimizar a função de perda. Normalmente, essa atualização é realizada com o uso de um algoritmo de otimização, como o gradiente descendente estocástico (SGD), que discutimos anteriormente.

5. Processo iterativo: As etapas 1 a 4 são repetidas iterativamente por um número fixo de épocas ou até que os critérios de convergência sejam atendidos. Durante cada iteração, os parâmetros da rede são ajustados com base nos gradientes calculados na passagem para trás, reduzindo gradualmente a perda e melhorando o desempenho do modelo.

Preparação de dados para o Perceptron de múltiplas camadas

A preparação dos dados para o treinamento de um MLP envolve a limpeza, o pré-processamento, o dimensionamento, a divisão, a formatação e talvez até mesmo o aumento dos dados. Com base nas funções de ativação usadas e na escala dos recursos de entrada, os dados podem precisar ser padronizados ou normalizados. Experimentar diferentes técnicas de pré-processamento e avaliar seu impacto no desempenho do modelo geralmente é necessário para determinar a abordagem mais adequada para um conjunto de dados e uma tarefa específicos.

• Limpeza e pré-processamento de dados
• Lidar com valores ausentes: Remover ou imputar valores ausentes no conjunto de dados.
• Codificar variáveis categóricas: Converter variáveis categóricas em representações numéricas, como a codificação de um ponto.

• Dimensionamento de recursos
• Padronização ou normalização: Redimensione os recursos para uma escala semelhante a fim de garantir que o processo de otimização converja de forma eficiente.
• Padronização (normalização de escore Z): Subtraia a média e divida pelo desvio padrão de cada recurso. Ele centraliza os dados em torno de zero e os dimensiona para que tenham variância unitária.
• Normalização (escala Mín-Máx): Dimensione os recursos para um intervalo fixo, normalmente entre 0 e 1, subtraindo o valor mínimo e dividindo pelo intervalo (max-min).

Para saber mais sobre dimensionamento de recursos, confira o curso Engenharia de recursos para aprendizado de máquina em Python da Datacamp.

• Divisão entre treinamento, validação e teste
• Divida o conjunto de dados em conjuntos de treinamento, validação e teste. O conjunto de treinamento é usado para treinar o modelo, o conjunto de validação é usado para ajustar os hiperparâmetros e monitorar o desempenho do modelo, e o conjunto de teste é usado para avaliar o desempenho do modelo final em dados não vistos.

• Formatação de dados
• Certifique-se de que os dados estejam no formato apropriado para o treinamento. Isso pode envolver a reformulação dos dados ou a conversão para o tipo de dados necessário (por exemplo, conversão de variáveis categóricas em numéricas).

• Ampliação opcional de dados
• Para tarefas como classificação de imagens, técnicas de aumento de dados, como rotação, inversão e dimensionamento, podem ser aplicadas para aumentar a diversidade dos dados de treinamento e melhorar a generalização do modelo.

• Funções de normalização e ativação
• A escolha entre padronização e normalização pode depender das funções de ativação usadas no MLP. Funções de ativação como sigmoide e tanh são sensíveis à escala dos dados de entrada e podem se beneficiar da padronização. Por outro lado, as funções de ativação, como a ReLU, são menos sensíveis à escala e podem não exigir padronização.

Diretrizes gerais para a implementação do Multilayer Perceptron

A implementação de um MLP envolve várias etapas, desde o pré-processamento de dados até o treinamento e a avaliação do modelo. A seleção do número de camadas e neurônios para um MLP envolve o equilíbrio entre a complexidade do modelo, o tempo de treinamento e o desempenho da generalização. Não existe uma resposta única para todos os casos, pois a arquitetura ideal depende de fatores como a complexidade da tarefa, a quantidade de dados disponíveis e os recursos computacionais. Entretanto, aqui estão algumas diretrizes gerais a serem consideradas ao implementar o MLP:

1. Arquitetura do modelo

• Comece com uma arquitetura simples e aumente gradualmente a complexidade conforme necessário. Comece com uma única camada oculta e um pequeno número de neurônios e, em seguida, experimente adicionar mais camadas e neurônios, se necessário.

2. Complexidade da tarefa

• Para tarefas simples com complexidade relativamente baixa, como classificação binária ou regressão em pequenos conjuntos de dados, uma arquitetura superficial com menos camadas e neurônios pode ser suficiente.
• Para tarefas mais complexas, como classificação multiclasse ou regressão em dados de alta dimensão, podem ser necessárias arquiteturas mais profundas com mais camadas e neurônios para capturar padrões intrincados nos dados.

3. Pré-processamento de dados

• Limpe e pré-processe seus dados, incluindo o tratamento de valores ausentes, a codificação de variáveis categóricas e o dimensionamento de recursos numéricos.
• Divida seus dados em conjuntos de treinamento, validação e teste para avaliar o desempenho do modelo.

4. Inicialização

• Inicialize adequadamente os pesos e as polarizações de seu MLP. As técnicas comuns de inicialização incluem a inicialização aleatória com pesos pequenos ou o uso de técnicas como a inicialização Xavier ou He.

5. Experimentação

• Por fim, a melhor abordagem é experimentar diferentes arquiteturas, variando o número de camadas e neurônios, e avaliar seu desempenho empiricamente.
• Use técnicas como validação cruzada e ajuste de hiperparâmetros para explorar sistematicamente diferentes arquiteturas e encontrar a que apresenta o melhor desempenho na tarefa em questão.

6. Treinamento

• Treine seu MLP usando os dados de treinamento e monitore seu desempenho no conjunto de validação.
• Faça experiências com diferentes tamanhos de lote, número de épocas e outros hiperparâmetros para encontrar as configurações de treinamento ideais.
• Visualize o progresso do treinamento usando métricas como perda e precisão para diagnosticar problemas e acompanhar a convergência.

7. Algoritmo de otimização

• Faça experimentos com diferentes taxas de aprendizagem e considere o uso de técnicas como cronogramas de taxa de aprendizagem ou taxas de aprendizagem adaptáveis.

8. Evite o ajuste excessivo

• Tenha cuidado para não ajustar demais o modelo aos dados de treinamento, introduzindo uma complexidade desnecessária.
• Use técnicas como regularização (por exemplo, regularização L1, L2), abandono e parada antecipada para evitar o excesso de ajuste e melhorar o desempenho da generalização.
• Ajuste a força da regularização com base no desempenho do modelo no conjunto de validação.

9. Avaliação do modelo

• Monitore o desempenho do modelo em um conjunto de validação separado durante o treinamento para avaliar como as alterações na arquitetura afetam o desempenho.
• Avalie o modelo treinado no conjunto de teste para avaliar seu desempenho de generalização.
• Use métricas como precisão, perda e erro de validação para avaliar o desempenho do modelo e orientar as decisões de arquitetura.

10. Iterar e experimentar

• Faça experiências com diferentes arquiteturas, hiperparâmetros e estratégias de otimização para melhorar o desempenho do modelo.
• Itere sua implementação com base nos insights obtidos com os resultados do treinamento e da avaliação.

Conclusão

Os perceptrons multicamadas representam uma classe fundamental e versátil de redes neurais artificiais que contribuíram significativamente para o avanço do aprendizado de máquina e da inteligência artificial. Por meio de suas camadas interconectadas de neurônios e funções de ativação não lineares, os MLPs são capazes de aprender padrões e relacionamentos complexos nos dados, o que os torna adequados para uma ampla gama de tarefas. A história dos MLPs reflete uma jornada de exploração, descoberta e inovação, desde os primeiros modelos de perceptron até as modernas arquiteturas de aprendizagem profunda que alimentam muitos sistemas de última geração atualmente.

Neste artigo, você aprendeu os conceitos básicos das redes neurais artificiais, concentrou-se nos perceptrons multicamadas, aprendeu sobre a descida do gradiente estocástico e a retropropagação. Se você estiver interessado em obter experiência prática e usar técnicas de aprendizagem profunda para solucionar desafios do mundo real, como prever preços de imóveis, criar redes neurais para modelar imagens e textos, recomendamos seguir a trilha da caixa de ferramentas Keras do Datacamp.

Trabalhando com o Keras, você aprenderá sobre redes neurais, fluxos de trabalho de modelos de aprendizagem profunda e como otimizar seus modelos. O Datacamp também tem uma folha de dicas sobre o Keras que pode ser útil!