Hadamard-Produkt: Ein kompletter Leitfaden zur elementweisen Matrixmultiplikation

Dieses Tutorial geht auf die mathematischen Grundlagen, die rechnerischen Eigenschaften und die vielfältigen Anwendungen des Hadamard-Produkts ein. Anhand von praktischen Beispielen wirst du sehen, wie dieser Vorgang theoretische Mathematik mit Datenwissenschaft-Anwendungen verbindet und so zu einem unverzichtbaren Werkzeug für alle wird, die mit Matrizen und hochdimensionalen Daten arbeiten.

Wenn du eine solide Basis in Matrixoperationen aufbauen willst, schau dir unseren Kurs „Lineare Algebra für Data Science in R“ an. Dort lernst du wichtige Konzepte, die das Hadamard-Produkt ergänzen. 

Definition und mathematische Notation

Das Hadamard-Produkt, auch als elementweise Multiplikation bekannt, ist eine der vielseitigsten Operationen in der Matrixalgebra. Anders als bei der normalen Matrixmultiplikation werden hier Matrizen durch Multiplikation der entsprechenden Elemente kombiniert, sodass die ursprünglichen Dimensionen erhalten bleiben und gleichzeitig lokale Transformationen möglich sind.

Formale Definition

Angenommen, wir haben zwei Matrizen A und B, die beide die Größe m × n, bilden ein Hadamard-Produkt A ∘ B (oder manchmal auch als A ⊙ B) berechnet, indem man die entsprechenden Elemente miteinander multipliziert:

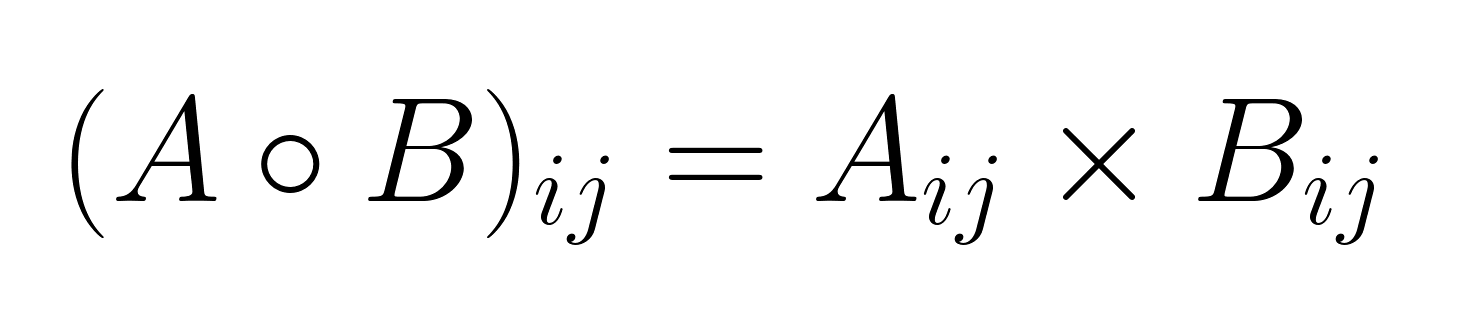
wo i zwischen 1 und m und j geht von 1 bis n.

Die Matrix, die wir bekommen, ist C = A ∘ B hat die gleichen Abmessungen wie die Eingabematrizen, wobei jedes Element unabhängig von den anderen berechnet wird.

Standardnotation und Konventionen

Für das Hadamard-Produkt gibt es mehrere Schreibweisen:

• (hohler Punkt): Die gängigste mathematische Notation
• (eingekreister Punkt): Alternatives mathematisches Symbol
• .*: Wird in Programmiersprachen wie MATLAB benutzt.
• *: Elementweiser Multiplikationsoperator in NumPy und anderen Bibliotheken

Die Wahl der Notation hängt oft vom Kontext und Anwendungsbereich ab, obwohl ∘ in der mathematischen Literatur der Standard bleibt.

Schritt-für-Schritt-Beispiel

Lass uns das Hadamard-Produkt mit zwei 3×2-Matrizen anschaulich erklären:

Matrix A:

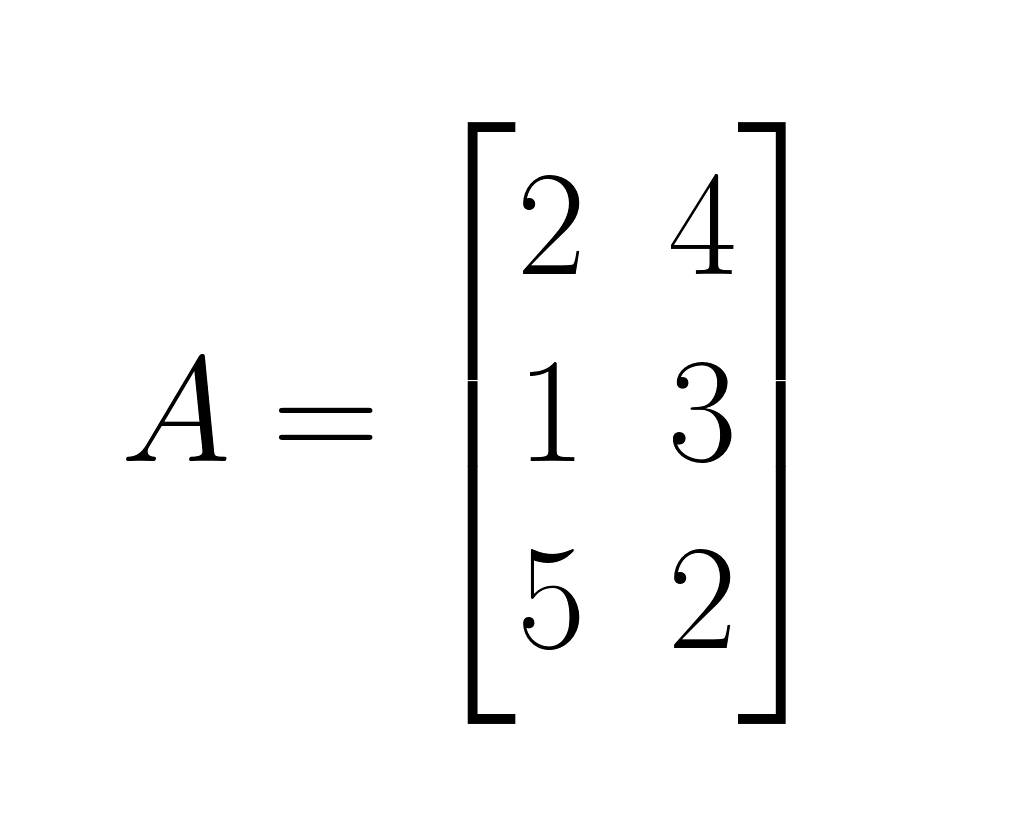
Matrix B:

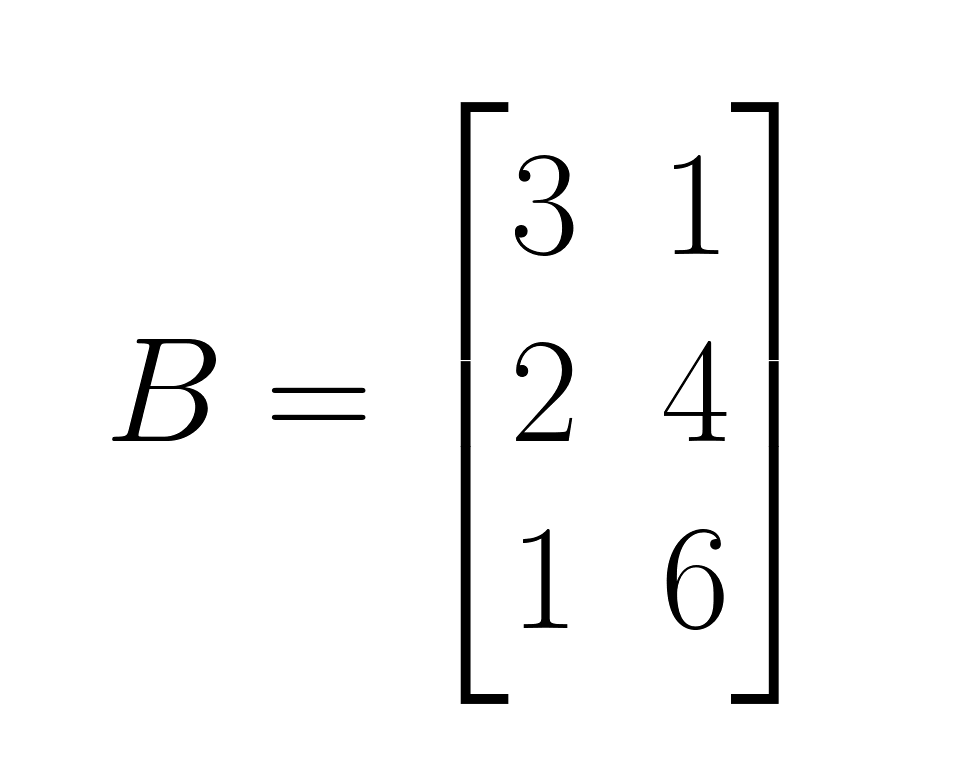
A ∘ B:

• Schritt 1: Multipliziere die gleichen Elemente an Position (1,1): 2 × 3 = 6 
• Schritt 2: Multipliziere die gleichen Elemente an Position (1,2): 4 × 1 = 4 
• Schritt 3: Multipliziere die gleichen Elemente an Position (2,1): 1 × 2 = 2 
• Schritt 4: Multipliziere die gleichen Elemente an Position (2,2): 3 × 4 = 12 
• Schritt 5: Multipliziere die gleichen Elemente an Position (3,1): 5 × 1 = 5 
• Schritt 6: Multipliziere die gleichen Elemente an Position (3,2): 2 × 6 = 12

Hier ist das Ergebnis:

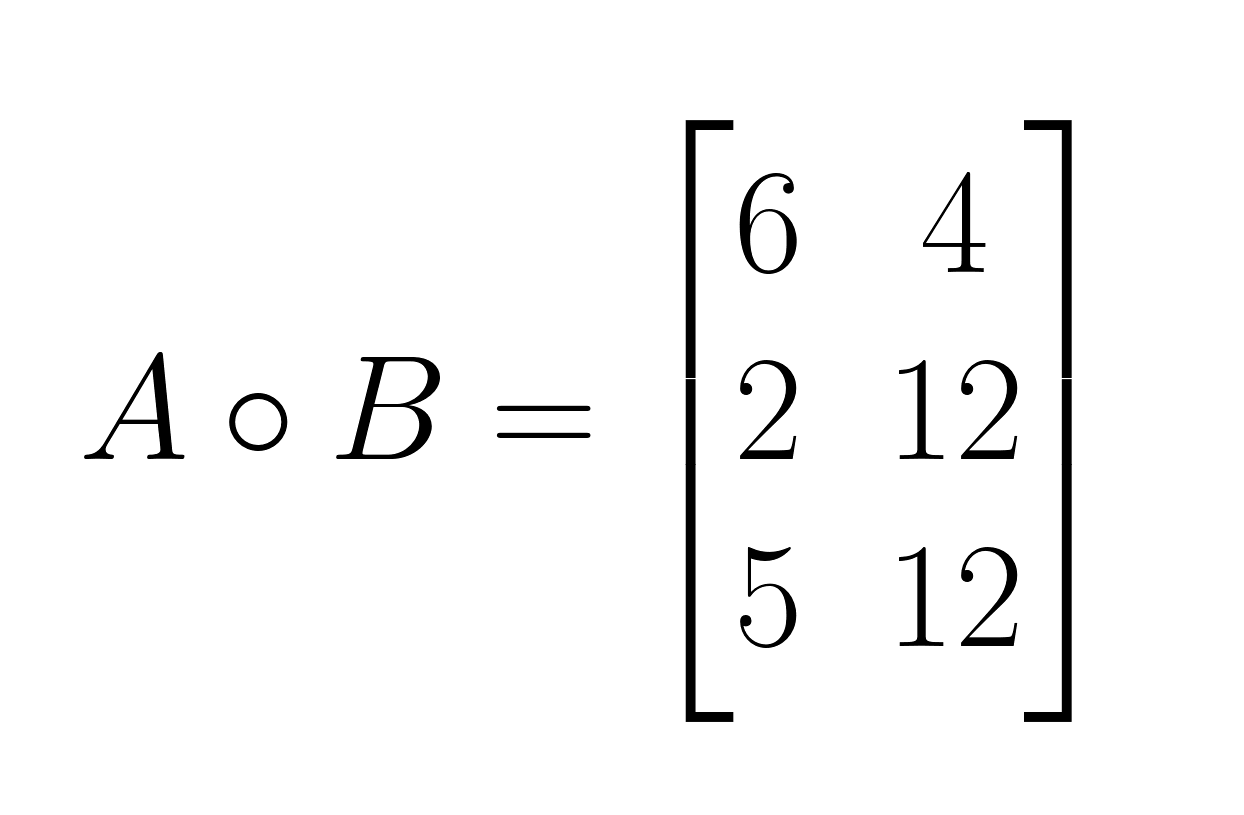
Wichtige Einschränkungen

Das Hadamard-Produkt hat eine strenge Anforderung an die Dimensionen: Beide Matrizen müssen die gleichen Dimensionen haben. Anders als bei der normalen Matrixmultiplikation, wo die inneren Dimensionen übereinstimmen müssen, muss beim Hadamard-Produkt alles in den Dimensionen passen. Diese Einschränkung stellt sicher, dass jedes Element in einer Matrix ein passendes Element in der anderen Matrix für die Multiplikation hat. Wenn Matrizen unterschiedliche Dimensionen haben, ist das Hadamard-Produkt nicht definiert.

Grundlegende und erweiterte Eigenschaften

Das Hadamard-Produkt hat ganz besondere algebraische Eigenschaften, die es von der normalen Matrixmultiplikation unterscheiden. Wenn man diese Eigenschaften versteht, wird klar, warum die elementweise Multiplikation anders funktioniert, und man bekommt einen Einblick in ihre mathematische Struktur.

Eigenschaften

Kommutativität

Das Hadamard-Produkt ist kommutativ, das heißt, die Reihenfolge der Multiplikation hat keinen Einfluss auf das Ergebnis:

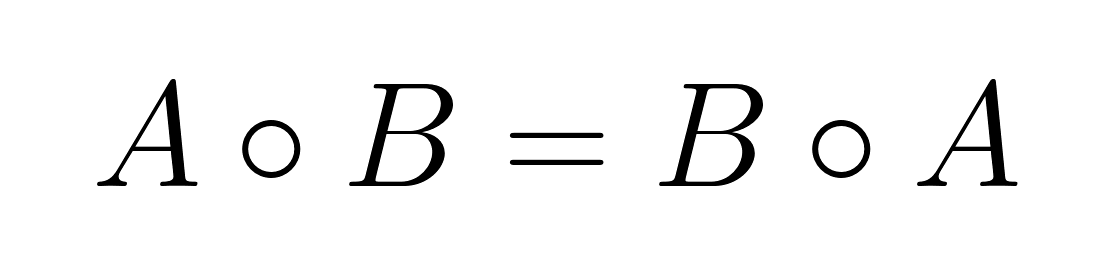
Diese Eigenschaft gilt, weil die elementweise Multiplikation von reellen Zahlen kommutativ ist: aᵢⱼ × bᵢⱼ = bᵢⱼ × aᵢⱼ.

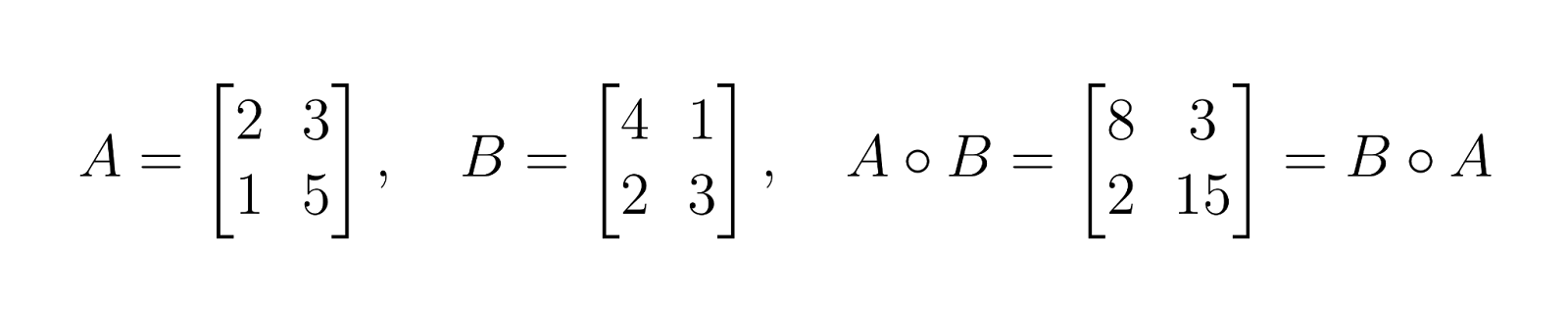
Das ist anders als bei der Matrixmultiplikation, die normalerweise nicht kommutativ ist.

Assoziativität

Das Hadamard-Produkt ist assoziativ, was die Gruppierung von Operationen ohne Änderung des Ergebnisses ermöglicht:

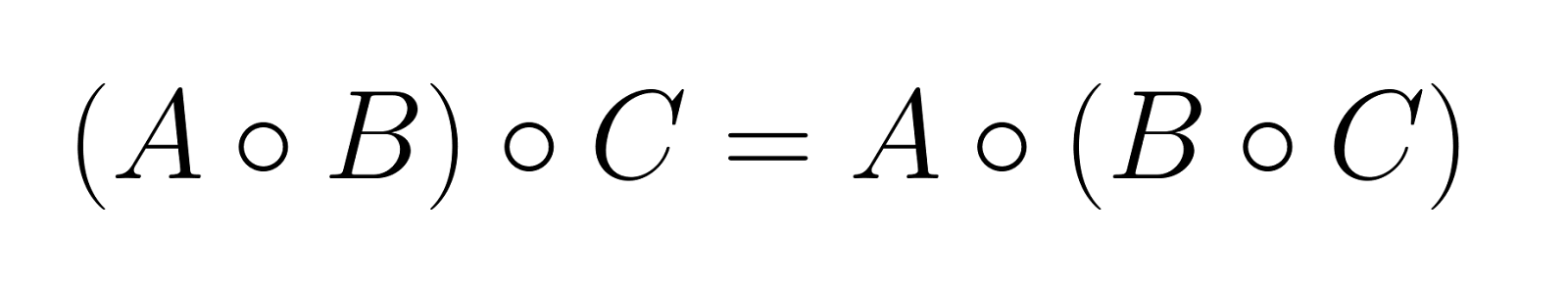
Diese Eigenschaft gilt für beliebig viele Matrizen, solange sie alle die gleichen Abmessungen haben.

Verteilbarkeit mit Matrixaddition

Das Hadamard-Produkt lässt sich auf die Matrixaddition verteilen:

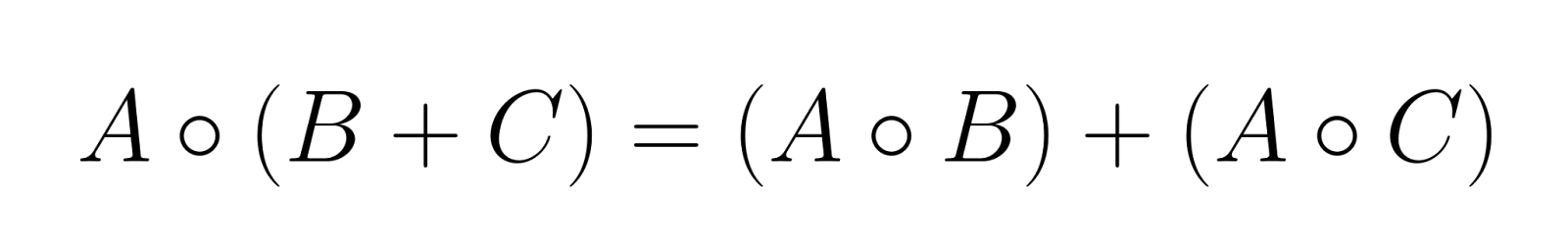
Diese Eigenschaft macht das Hadamard-Produkt mit linearen Kombinationen von Matrizen kompatibel.

Identitätselement

Das Identitätselement für das Hadamard-Produkt ist die Matrix aus lauter Einsen, J, wo jedes Element gleich 1 ist. Für jedeMatrix t A:

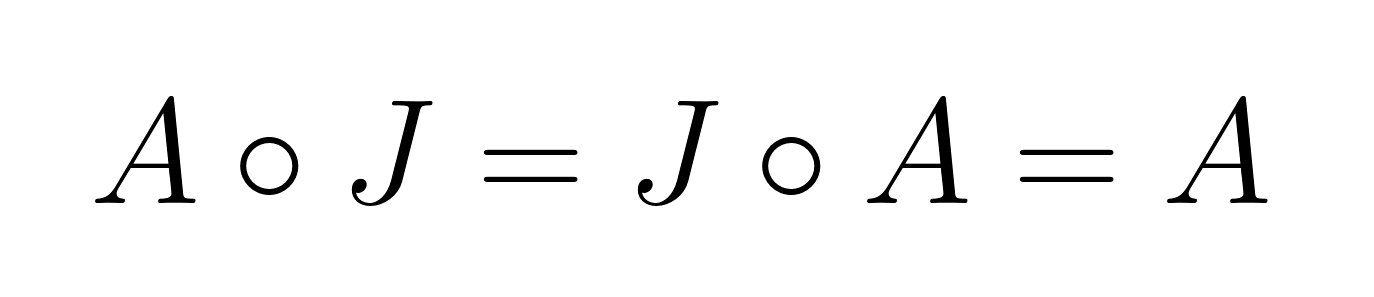
Das ist ganz anders als bei der normalen Matrixmultiplikation, wo die Einheitsmatrix nur Einsen auf der Diagonalen und sonst Nullen hat.

Vergleich mit der normalen Matrixmultiplikation

Anders als bei der normalen Matrixmultiplikation gilt für das Hadamard-Produkt:

• Braucht Matrizen mit den gleichen Abmessungen.
• Erzeugt ein Ergebnis mit denselben Abmessungen wie die Eingabematrizen.
• Ist immer kommutativ
• Hat ein anderes Identitätselement
• Erfüllt nicht die gemischte Assoziativität: (AB) ∘ C ≠ A(B ∘ C) im Allgemeinen

Die Eigenschaft gemischter Produkte

Die Eigenschaft gemischter Produkte stellt eine Beziehung zwischen dem Hadamard-Produkt und der Matrix-Transposition her:

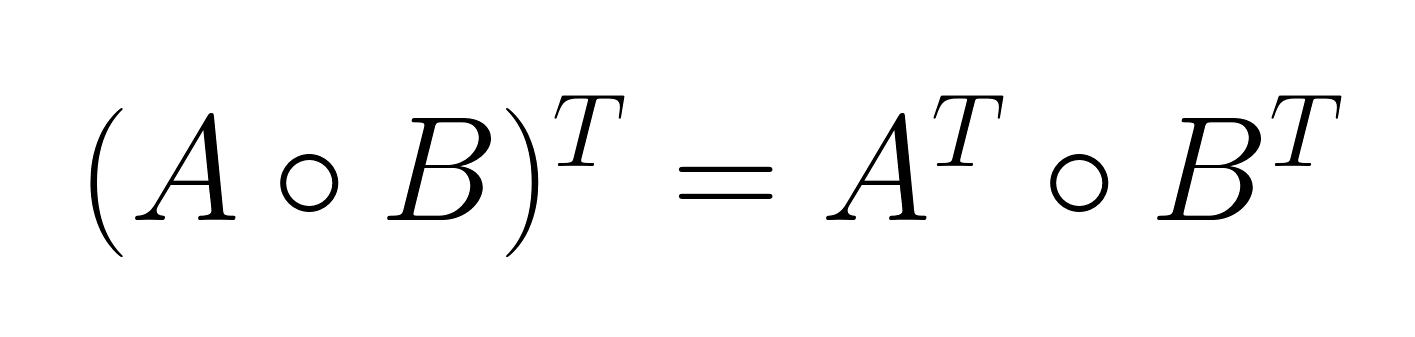
Diese Eigenschaft ist besonders nützlich bei Optimierungsproblemen und statistischen Anwendungen, wo transponierte Matrizen oft vorkommen.

Hier ist ein Beispiel: Bei der Schätzung der Kovarianzmatrixation arbeiten Forscher oft mit transponierten Datenmatrizen. Die Eigenschaft gemischter Produkte ermöglicht elementweise Operationen vor oder nach der Transposition, was beim Entwerfen von Algorithmen für mehr Flexibilität beim Rechnen sorgt.

Schur-Produktsatz und positive Semidefinitheit

Der Schur-Satz ist einer der wichtigsten theoretischen Ergebnisse zum Hadamard-Produkt. Es besagt, dass das Hadamard-Produkt zweier positiv semidefiniter Matrizen auch positiv semidefinit ist.

Satz: Wenn die Matrizen A und B positiv semidefinit und gleich groß sind, dann ist auchA ∘ B positiv semidefinit.

Auswirkungen auf die Matrixanalyse

Dieser Satz hat ein paar wichtige Folgen:

• Erhaltung der positiven Semidefinitheit: Die Eigenschaft sorgt dafür, dass bestimmte Matrixoperationen die gewünschten mathematischen Eigenschaften behalten. In der statistischen Modellierung zeigen positiv semidefinite Matrizen gültige Kovarianzstrukturen, und der Satz garantiert, dass die elementweise Multiplikation diese Gültigkeit beibehält.
• Zusammenhang mit dem Matrixrang: Das Hadamard-Produkt behält normalerweise den Matrixrang nicht bei. Der Rang von„ A ∘ B” kann kleiner, gleich oder (in besonderen Fällen) größer sein als der kleinere Wert von „rank(A)” und „rank(B)”.
• Eigenwertbeziehungen: Während das Hadamard-Produkt keine einfache Beziehung zu den Eigenwerten der ursprünglichen Matrizen hat, gibt der Schur-Produktsatz Grenzen für die Eigenwerte des Ergebnisses, wenn es um positiv semidefinite Matrizen geht.

Berechnung und Umsetzung

Die Berechnungsmerkmale des Hadamard-Produkts machen es besonders cool für Anwendungen in der Verarbeitung großer Datenmengen. Wenn man weiß, wie es funktioniert und was man bei der Implementierung beachten muss, kann man die Leistung in Rechnerumgebungen optimieren.

Effizienz und Rechenaufwand

Komplexitätsanalyse

Das Hadamard-Produkt hat eine Zeitkomplexität von O(mn) für zwei Matrizen der Größe m × n, wobei jedes Element genau eine Multiplikationsoperation erfordert. Diese lineare Komplexität ist ganz anders als bei der normalen Matrixmultiplikation, die bei quadratischen Matrizen mit herkömmlichenAlgorithmen eine Komplexität vonO( O(n³)) hat.

Auswirkungen auf die Verarbeitung in großem Maßstab

Die lineare Komplexität macht das Hadamard-Produkt besonders gut für Folgendes:

• Hochdimensionale Datensätze: Bei Matrizen mit Millionen von Elementen sorgt die Komplexität O(mn) dafür, dass die Verarbeitungszeiten mit der Datengröße vorhersehbar skalieren.
• Echtzeit-Anwendungen: Der minimale Rechenaufwand ermöglicht elementweise Operationen in zeitkritischen Szenarien wie Bildverarbeitungs-Pipelines und neuronalen Netzwerken.
• Speichereffizienz: Da jedes Element unabhängig verarbeitet wird, kann man bei der Implementierung Streaming oder blockweise Verarbeitung nutzen, um Datensätze zu verarbeiten, die größer sind als der verfügbare Speicher.

Elementweise Multiplikation in der Praxis

Überlegungen zur Matrixverarbeitung

Bei der Berechnung des Hadamard-Produkts gibt's ein paar praktische Dinge zu beachten:

• Speicherlayout: Die Speichermethode „zeilenorientiert“ oder „spaltenorientiert“ beeinflusst die Cache-Leistung. Die meisten Implementierungen profitieren davon, wenn die Elemente in der Reihenfolge verarbeitet werden, in der sie im Speicher stehen.
• Vektorisierung: Moderne Prozessoren können SIMD-Operationen (Single Instruction, Multiple Data) machen, die mehrere Sachen gleichzeitig verarbeiten und so die Rechenleistung echt beschleunigen.
• Parallelisierung: Die Unabhängigkeit der einzelnen Operationen macht das Hadamard-Produkt super parallelisierbar über mehrere CPU-Kerne oder GPU-Threads.

Tensor-Kontexte und Herausforderungen

Bei der Erweiterung auf höherdimensionale Tensoren kommt es zu zusätzlichen Komplexitäten:

• Rundfunk: Viele Implementierungen unterstützen Broadcasting, was die elementweise Multiplikation zwischen Tensoren unterschiedlicher, aber kompatibler Formen ermöglicht.
• Speicherausrichtung: Bei Tensor-Operationen muss man echt auf die Speicherausrichtung achten, um die Leistung zu maximieren, vor allem auf spezieller Hardware wie GPUs und TPUs.
• Algorithmusoptimierung: Fortschrittliche Algorithmen wie HaTT (Hadamard-Transformation für Tensoren) bieten optimierte Implementierungen für bestimmte Tensorenstrukturen und sparen so Zeit und Speicherplatz in bestimmten Szenarien.

Umsetzung in Programmiersprachen

Python mit NumPy

NumPy macht das Hadamard-Produkt ganz einfach mit dem Operator „ * “:

import numpy as np

# Define matrices
A = np.array([[2, 4], [1, 3], [5, 2]])
B = np.array([[3, 1], [2, 4], [1, 6]])

# Compute Hadamard product
C = A * B
print(C)
# Output: [[ 6  4]
#          [ 2 12]
#          [ 5 12]]

# Alternative explicit notation
C_explicit = np.multiply(A, B)

Leistungsoptimierung in NumPy:

# For large matrices, ensure proper data types
A = A.astype(np.float32)  # Use float32 for memory efficiency
B = B.astype(np.float32)

# Pre-allocate output array for memory efficiency
C = np.empty_like(A)
np.multiply(A, B, out=C)

Andere Sprachen und Bibliotheken

R:

# C <- A * B  # Element-wise multiplication is default

matrix1 <- matrix(
  c(1, 2, 3,
    4, 5, 6,
    7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)

# Create the second matrix (3x3)
matrix2 <- matrix(
  c(9, 8, 7,
    6, 5, 4,
    3, 2, 1),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)

matrix1
matrix2
matrix1 * matrix2

     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6
[3,]    7    8    9
     [,1] [,2] [,3]
[1,]    9    8    7
[2,]    6    5    4
[3,]    3    2    1
     [,1] [,2] [,3]
[1,]    9   16   21
[2,]   24   25   24
[3,]   21   16    9

Julia:

C = A .* B  # Broadcasting element-wise multiplication	

Häufige Fehler und bewährte Vorgehensweisen

Typkompatibilität: Stell sicher, dass die Matrizen kompatible Datentypen haben, um unerwartete Typumwandlungen oder Genauigkeitsverluste zu vermeiden.

# Avoid mixing integer and float types unnecessarily
A = np.array([[1, 2]], dtype=np.int32)
B = np.array([[1.5, 2.5]], dtype=np.float64)
C = A * B  # Results in float64, may not be intended

Aufklärung über Rundfunk: Versteh, wie Broadcasting funktioniert, um ungewollte Dimensionserweiterungen zu vermeiden.

# Be explicit about intended operations
A = np.array([[1, 2, 3]])      # Shape: (1, 3)
B = np.array([[1], [2], [3]])  # Shape: (3, 1)
C = A * B  # Results in (3, 3) matrix due to broadcasting

Speicherverwaltung: Für große Operationen solltest du In-Place-Operationen und die Vorabzuweisung von Speicher in Betracht ziehen.

# In-place operation to save memory
A *= B  # Modifies A directly

# Pre-allocate for repeated operations
result = np.empty((1000, 1000))
for i in range(iterations):
    np.multiply(matrix1, matrix2, out=result)

Pipeline-Integration: Stell in Workflows für maschinelles Lernen sicher, dass Hadamard-Operationen reibungslos mit automatischen Differenzierungsframeworks zusammenarbeiten und den Gradientenfluss aufrechterhalten.

Anwendungen in verschiedenen Bereichen

Das Hadamard-Produkt wird bei Operationen verwendet, die lokale Transformationen erfordern, während die Matrixstruktur erhalten bleibt.

Bildbearbeitung

Das Hadamard-Produkt ist super wichtig für die JPEG-Decodierung, wo es Quantisierungsmatrizen mit transformierten Bildkoeffizienten kombiniert, um visuelle Daten wiederherzustellen. Bei der Bildverbesserung kann man damit bestimmte Sachen machen, wie zum Beispiel Rauschen durch elementweise Multiplikation mit Filtermasken zu reduzieren und durch räumliche Gewichtungsmatrizen auf Pixelgruppen die Schärfe oder Unschärfe kontrolliert anzupassen.

Statistische Modellierung und Datenanalyse

Das Hadamard-Produkt macht gewichtete Regression einfacher, indem es Gewichte auf einzelne Elemente von Designmatrizen anwendet, und hilft bei der robusten Schätzung von Kovarianzen durch selektive Skalierung von Matrixelementen. Die Operation ist super wichtig bei Kernel-Methoden und semidefiniter Programmierung, weil sie die positive semidefinite Eigenschaft beibehält, die für valide statistische Modelle nötig ist. Das macht sie super nützlich für Regularisierungstechniken, die elementweise Beschränkungen auf Kovarianzstrukturen anwenden.

Tiefes Lernen und neuronale Netze

Das Hadamard-Produkt taucht oft in rekurrenten neuronalen Netzwerkarchitekturen auf, vor allem in GRUs und LSTMs, wo es den Informationsfluss durch elementweise Gating-Mechanismen steuert. Moderne Architekturen wie StyleGAN und SENet nutzen es für die adaptive Skalierung von Merkmalen, während Aufmerksamkeitsmechanismen elementweise Multiplikation verwenden, um Merkmalsdarstellungen zu gewichten, was sowohl die Modelleffizienz als auch die Leistung bei der Sequenzmodellierung und generativen Aufgaben deutlich verbessert.

Andere coole Anwendungen

Das Hadamard-Produkt wird auch in der Signalverarbeitung für Frequenzbereichsfilterung und Spektralanalyse verwendet, wo die elementweise Multiplikation mit Übertragungsfunktionen die Signaleigenschaften verändert. In der Graphentheorie kann man damit an Adjazenzmatrizen an Knoten arbeiten, während man in der Kombinatorik Zählmatrizen elementweise bearbeiten und diskrete Optimierungsprobleme lösen kann.

Fazit

Wenn du mehr über die mathematischen Konzepte erfahren möchtest, die dem modernen maschinellen Lernen und Deep Learning zugrunde liegen, bietet unser Tutorial „Demystifying Mathematical Concepts for Deep Learning“ zusätzliche Einblicke in die mathematischen Grundlagen, die die heutigen KI-Innovationen vorantreiben. Melde dich außerdem für unseren Kurs „Linear Algebra for Data Science in R“ an, um dir ein solides Fundament aufzubauen.