Hadamard Product: A Complete Guide to Element-Wise Matrix Multiplication

This tutorial explores the mathematical foundations, computational characteristics, and wide-ranging applications of the Hadamard product. Through hands-on examples, you'll discover how this operation bridges theoretical mathematics with data science applications, making it an essential tool for anyone working with matrices and high-dimensional data.

To build a strong foundation in matrix operations, explore our Linear Algebra for Data Science in R course, which covers essential concepts that complement the Hadamard product. 

Definition and Mathematical Notation

The Hadamard product, also known as element-wise multiplication, represents one of the most versatile operations in matrix algebra. Unlike standard matrix multiplication, this operation combines matrices by multiplying corresponding elements, creating results that preserve the original dimensions while enabling localized transformations.

Formal definition

Given two matrices A and B, both of size m × n, their Hadamard product A ∘ B (or sometimes denoted as A ⊙ B) is computed by multiplying corresponding elements:

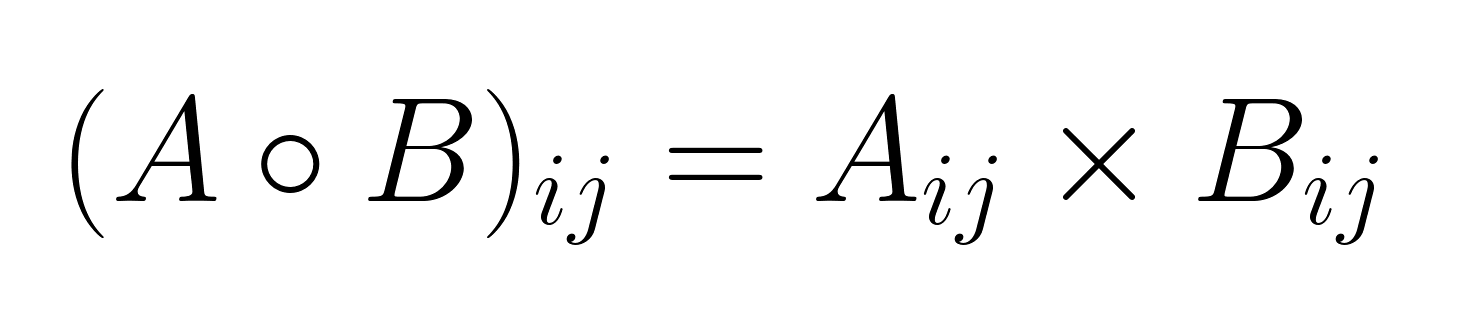
where i ranges from 1 to m and j ranges from 1 to n.

The resulting matrix C = A ∘ B has the same dimensions as the input matrices, with each element computed independently from the others.

Standard notation and conventions

Several notational conventions exist for the Hadamard product:

• ∘ (hollow dot): The most common mathematical notation
• ⊙ (circled dot): Alternative mathematical symbol
• .*: Used in programming languages like MATLAB
• *: Element-wise multiplication operator in NumPy and other libraries

The choice of notation often depends on the context and field of application, though ∘ remains the standard in mathematical literature.

Step-by-step example

Let's illustrate the Hadamard product with a concrete example using two 3×2 matrices:

Matrix A:

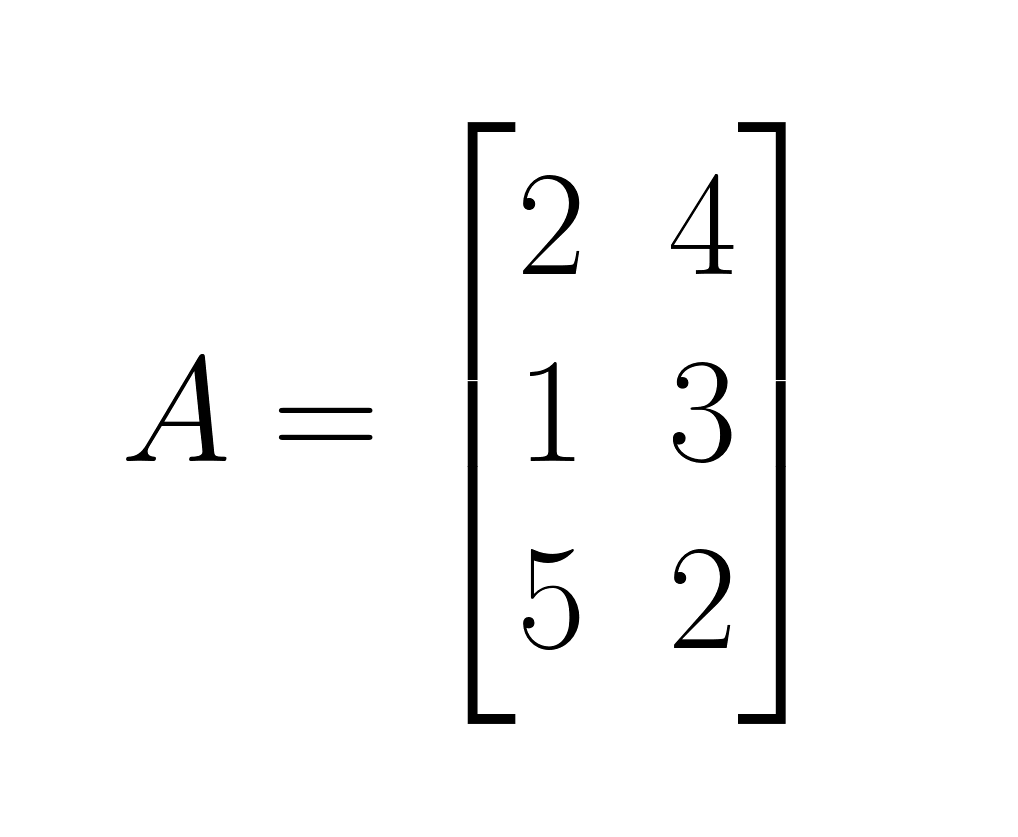
Matrix B:

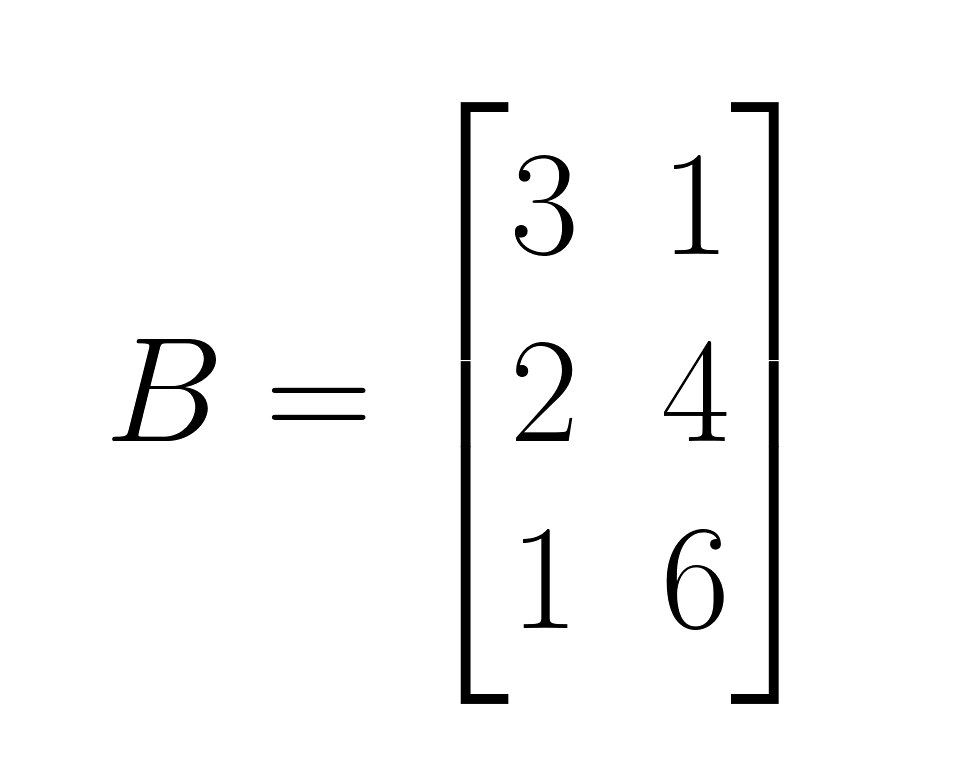
A ∘ B:

• Step 1: Multiply corresponding elements in position (1,1): 2 × 3 = 6 
• Step 2: Multiply corresponding elements in position (1,2): 4 × 1 = 4 
• Step 3: Multiply corresponding elements in position (2,1): 1 × 2 = 2 
• Step 4: Multiply corresponding elements in position (2,2): 3 × 4 = 12 
• Step 5: Multiply corresponding elements in position (3,1): 5 × 1 = 5 
• Step 6: Multiply corresponding elements in position (3,2): 2 × 6 = 12

Here is the result:

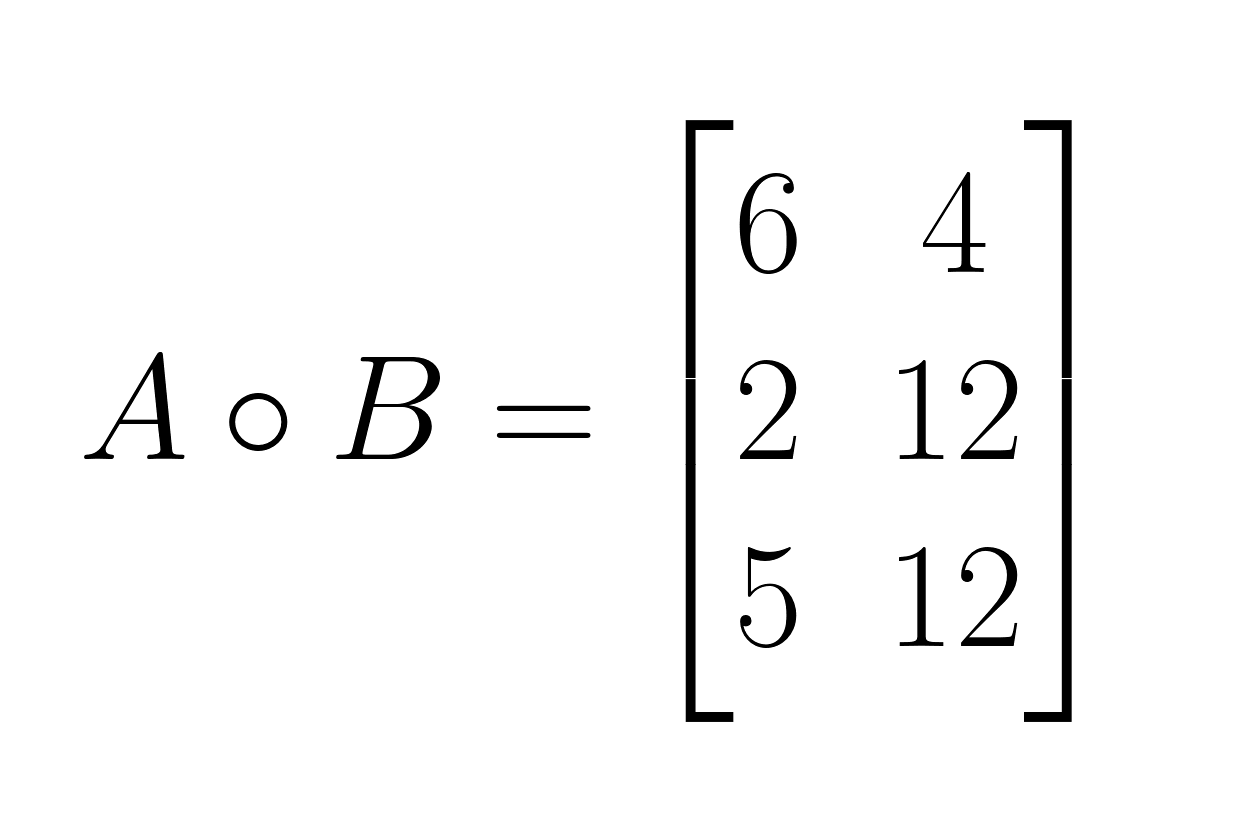
Important constraints

The Hadamard product has a strict dimensional requirement: both matrices must have identical dimensions. Unlike standard matrix multiplication, where the inner dimensions must match, the Hadamard product requires complete dimensional compatibility. This constraint ensures that every element in one matrix has a corresponding element in the other matrix for multiplication. When matrices have different dimensions, the Hadamard product is undefined.

Fundamental and Advanced Properties

The Hadamard product exhibits distinct algebraic properties that set it apart from standard matrix multiplication. Understanding these properties reveals why element-wise multiplication behaves differently and provides insights into its mathematical structure.

Basic properties

Commutativity

The Hadamard product is commutative, meaning the order of multiplication does not affect the result:

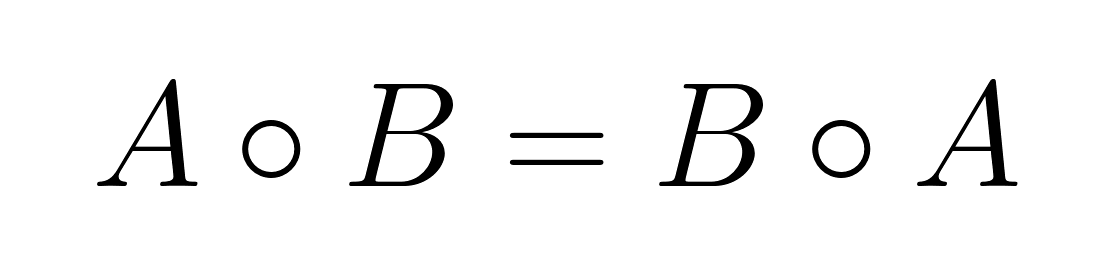
This property holds because element-wise multiplication of real numbers is commutative: aᵢⱼ × bᵢⱼ = bᵢⱼ × aᵢⱼ.

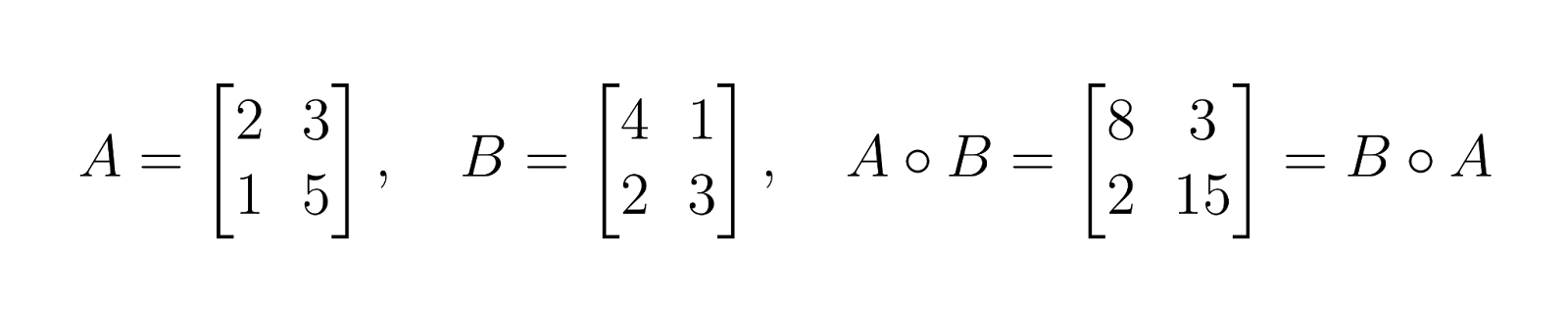
This is different than matrix multiplication, which is generally not commutative.

Associativity

The Hadamard product is associative, allowing grouping of operations without changing the result:

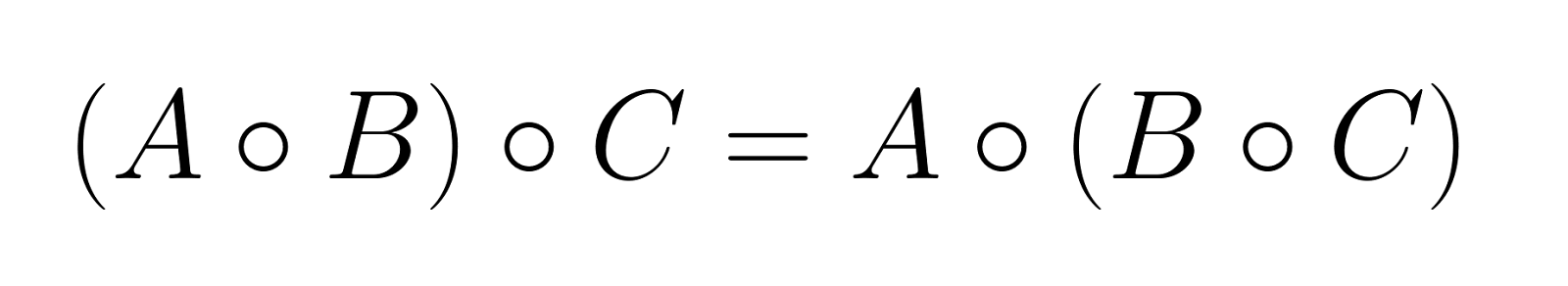
This property extends to any number of matrices, provided they all have identical dimensions.

Distributivity with matrix addition

The Hadamard product distributes over matrix addition:

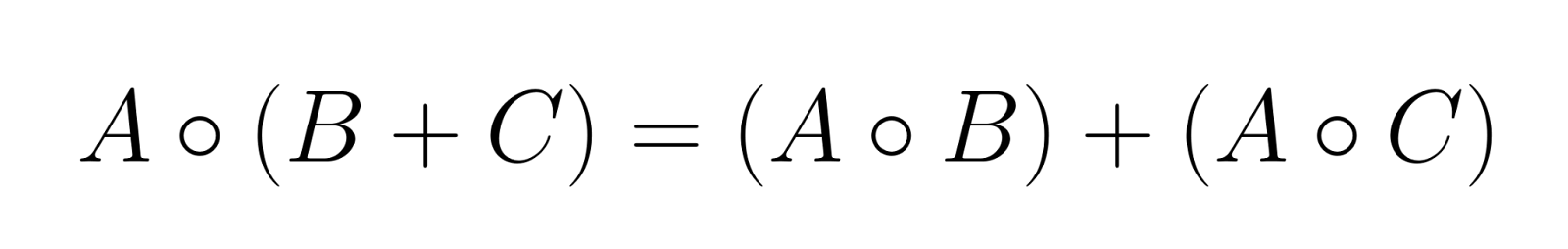
This property makes the Hadamard product compatible with linear combinations of matrices.

Identity element

The identity element for the Hadamard product is the matrix of all ones, J, where every element equals 1. For any matrix A:

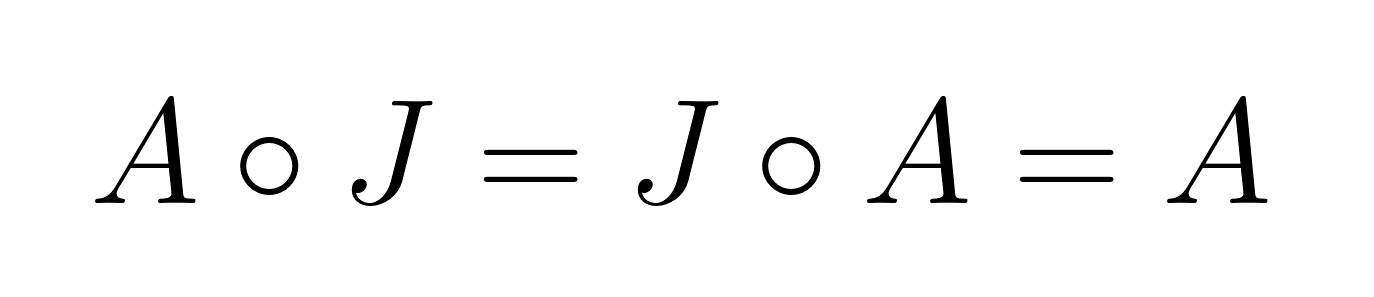
This differs significantly from standard matrix multiplication, where the identity matrix has ones on the diagonal and zeros elsewhere.

Comparison with standard matrix multiplication

Unlike standard matrix multiplication, the Hadamard product:

• Requires matrices of identical dimensions
• Produces a result with the same dimensions as the input matrices
• Is always commutative
• Has a different identity element
• Does not satisfy the mixed-associative property: (AB) ∘ C ≠ A(B ∘ C) in general

The mixed-product property

The mixed-product property establishes a relationship between the Hadamard product and matrix transposition:

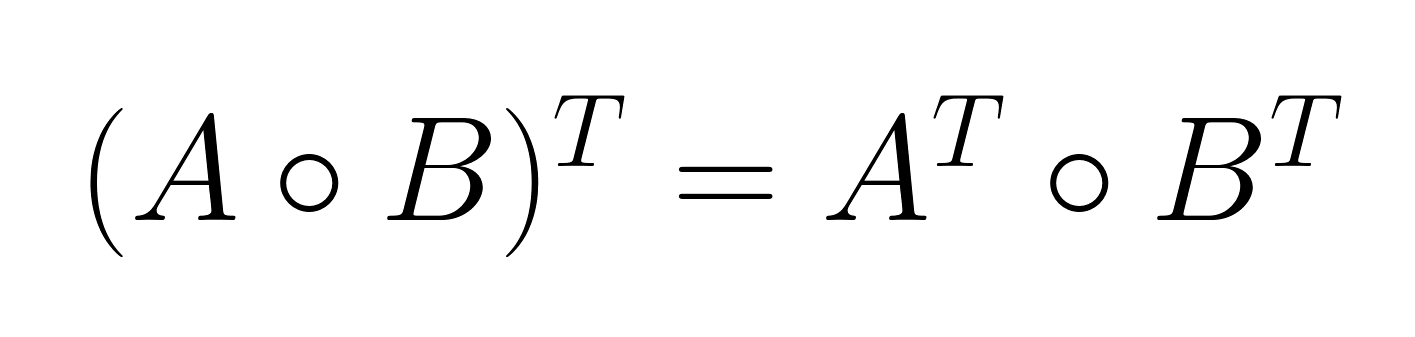
This property proves particularly useful in optimization problems and statistical applications where transposed matrices frequently appear.

xHere is an example scenario: In covariance matrix estimation, researchers often work with transposed data matrices. The mixed-product property allows element-wise operations to be performed before or after transposition, providing computational flexibility in algorithm design.

Schur product theorem and positive semidefiniteness

The Schur Product Theorem represents one of the most significant theoretical results regarding the Hadamard product. It states that the Hadamard product of two positive semidefinite matrices is also positive semidefinite.

Theorem: If A and B are positive semidefinite matrices of the same size, then A ∘ B is positive semidefinite.

Implications for matrix analysis

This theorem has several important consequences:

• Preserving positive semidefiniteness: The property ensures that certain matrix operations maintain desirable mathematical properties. In statistical modeling, positive semidefinite matrices represent valid covariance structures, and the theorem guarantees that element-wise multiplication preserves this validity.
• Connection to matrix rank: The Hadamard product generally does not preserve matrix rank. The rank of A ∘ B can be less than, equal to, or (in special cases) greater than the minimum of rank(A) and rank(B).
• Eigenvalue relationships: While the Hadamard product does not have a simple relationship with eigenvalues of the original matrices, the Schur Product Theorem provides bounds on the eigenvalues of the result when dealing with positive semidefinite matrices.

Computation and Implementation

The computational characteristics of the Hadamard product make it particularly attractive for large-scale data processing applications. Understanding its efficiency profile and implementation considerations helps optimize performance in computing environments.

Efficiency and computational complexity

Complexity analysis

The Hadamard product has a time complexity of O(mn) for two matrices of size m × n, where each element requires exactly one multiplication operation. This linear complexity contrasts sharply with standard matrix multiplication, which has a complexity of O(n³) for square matrices using conventional algorithms.

Implications for large-scale processing

The linear complexity makes the Hadamard product particularly suitable for:

• High-dimensional datasets: When working with matrices containing millions of elements, the O(mn) complexity ensures processing times scale predictably with data size.
• Real-time applications: The minimal computational overhead allows element-wise operations in time-sensitive scenarios such as image processing pipelines and neural network inference.
• Memory efficiency: Since each element is processed independently, implementations can leverage streaming or block-wise processing to handle datasets larger than available memory.

Element-wise multiplication in practice

Matrix processing considerations

Computing the Hadamard product involves several practical considerations:

• Memory layout: Row-major versus column-major storage affects cache performance. Most implementations benefit from processing elements in the same order as they appear in memory.
• Vectorization: Modern processors support SIMD (single instruction, multiple data) operations that can process multiple elements simultaneously, significantly accelerating computation.
• Parallelization: The independence of element-wise operations makes the Hadamard product highly parallelizable across multiple CPU cores or GPU threads.

Tensor contexts and challenges

When extending to higher-dimensional tensors, additional complexities arise:

• Broadcasting: Many implementations support broadcasting, allowing element-wise multiplication between tensors of different but compatible shapes.
• Memory alignment: Tensor operations require careful attention to memory alignment to maximize performance, particularly on specialized hardware like GPUs and TPUs.
• Algorithm optimization: Advanced algorithms like HaTT (Hadamard Transform for Tensors) provide optimized implementations for specific tensor structures, reducing both time and space complexity in certain scenarios.

Implementation in programming languages

Python with NumPy

NumPy provides straightforward Hadamard product implementation using the * operator:

import numpy as np

# Define matrices
A = np.array([[2, 4], [1, 3], [5, 2]])
B = np.array([[3, 1], [2, 4], [1, 6]])

# Compute Hadamard product
C = A * B
print(C)
# Output: [[ 6  4]
#          [ 2 12]
#          [ 5 12]]

# Alternative explicit notation
C_explicit = np.multiply(A, B)

Performance optimization in NumPy:

# For large matrices, ensure proper data types
A = A.astype(np.float32)  # Use float32 for memory efficiency
B = B.astype(np.float32)

# Pre-allocate output array for memory efficiency
C = np.empty_like(A)
np.multiply(A, B, out=C)

Alternative languages and libraries

R:

# C <- A * B  # Element-wise multiplication is default

matrix1 <- matrix(
  c(1, 2, 3,
    4, 5, 6,
    7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)

# Create the second matrix (3x3)
matrix2 <- matrix(
  c(9, 8, 7,
    6, 5, 4,
    3, 2, 1),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)

matrix1
matrix2
matrix1 * matrix2

     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6
[3,]    7    8    9
     [,1] [,2] [,3]
[1,]    9    8    7
[2,]    6    5    4
[3,]    3    2    1
     [,1] [,2] [,3]
[1,]    9   16   21
[2,]   24   25   24
[3,]   21   16    9

Julia:

C = A .* B  # Broadcasting element-wise multiplication	

Common pitfalls and best practices

Type compatibility: Ensure matrices have compatible data types to avoid unexpected type promotion or precision loss.

# Avoid mixing integer and float types unnecessarily
A = np.array([[1, 2]], dtype=np.int32)
B = np.array([[1.5, 2.5]], dtype=np.float64)
C = A * B  # Results in float64, may not be intended

Broadcasting awareness: Understand how broadcasting works to avoid unintended dimension expansion.

# Be explicit about intended operations
A = np.array([[1, 2, 3]])      # Shape: (1, 3)
B = np.array([[1], [2], [3]])  # Shape: (3, 1)
C = A * B  # Results in (3, 3) matrix due to broadcasting

Memory management: For large-scale operations, consider in-place operations and memory pre-allocation.

# In-place operation to save memory
A *= B  # Modifies A directly

# Pre-allocate for repeated operations
result = np.empty((1000, 1000))
for i in range(iterations):
    np.multiply(matrix1, matrix2, out=result)

Pipeline integration: In machine learning workflows, ensure Hadamard operations integrate smoothly with automatic differentiation frameworks and maintain gradient flow.

Applications Across Disciplines

The Hadamard product is used in operations that require localized transformations while preserving matrix structure.

Image processing

The Hadamard product plays a key role in JPEG decoding, where it combines quantization matrices with transformed image coefficients to reconstruct visual data. In image enhancement tasks, it enables selective operations like noise suppression through element-wise multiplication with filter masks, and controlled sharpening or blurring by applying spatial weight matrices to pixel neighborhoods.

Statistical modeling and data analysis

The Hadamard product facilitates weighted regression by applying element-wise weights to design matrices, and supports robust covariance estimation through selective scaling of matrix elements. The operation proves essential in kernel methods and semidefinite programming, where it preserves the positive semidefinite property required for valid statistical models, making it valuable for regularization techniques that apply element-wise constraints to covariance structures.

Deep learning and neural networks

The Hadamard product appears extensively in recurrent neural network architectures, particularly in GRUs and LSTMs, where it controls information flow through element-wise gating mechanisms. Modern architectures like StyleGAN and SENet use it for adaptive feature scaling, while attention mechanisms employ element-wise multiplication to weight feature representations, significantly improving both model efficiency and performance in sequence modeling and generative tasks.

Other notable applications

The Hadamard product extends to signal processing for frequency-domain filtering and spectral analysis, where element-wise multiplication with transfer functions modifies signal characteristics. In graph theory, it enables vertex-wise operations on adjacency matrices, while combinatorics applications include element-wise manipulation of counting matrices and discrete optimization problems.

Conclusion

If you are interested in exploring more mathematical concepts that underpin modern machine learning and deep learning, our Demystifying Mathematical Concepts for Deep Learning tutorial provides additional insights into the mathematical foundations that drive today's AI innovations, and enroll in our Linear Algebra for Data Science in R course for a strong foundation.