Produto de Hadamard: Um guia completo para multiplicação de matrizes elemento a elemento

Este tutorial fala sobre os fundamentos matemáticos, as características computacionais e as várias aplicações do produto de Hadamard. Com exemplos práticos, você vai descobrir como essa operação conecta a matemática teórica com as aplicações da ciência de dados, tornando-a uma ferramenta essencial para quem trabalha com matrizes e dados de alta dimensão.

Para construir uma base sólida em operações matriciais, dá uma olhada no nosso curso Álgebra Linear para Ciência de Dados em R, que aborda conceitos essenciais que complementam o produto de Hadamard. 

Definição e Notação Matemática

O produto de Hadamard, também conhecido como multiplicação elemento a elemento, é uma das operações mais versáteis da álgebra matricial. Diferente da multiplicação de matrizes padrão, essa operação junta matrizes multiplicando os elementos correspondentes, criando resultados que mantêm as dimensões originais e permitem transformações localizadas.

Definição formal

Dadas duas matrizes A e B, ambas com tamanho m × n, o produto de Hadamard deles A ∘ B (ou às vezes denotado como A ⊙ B) é calculado multiplicando os elementos correspondentes:

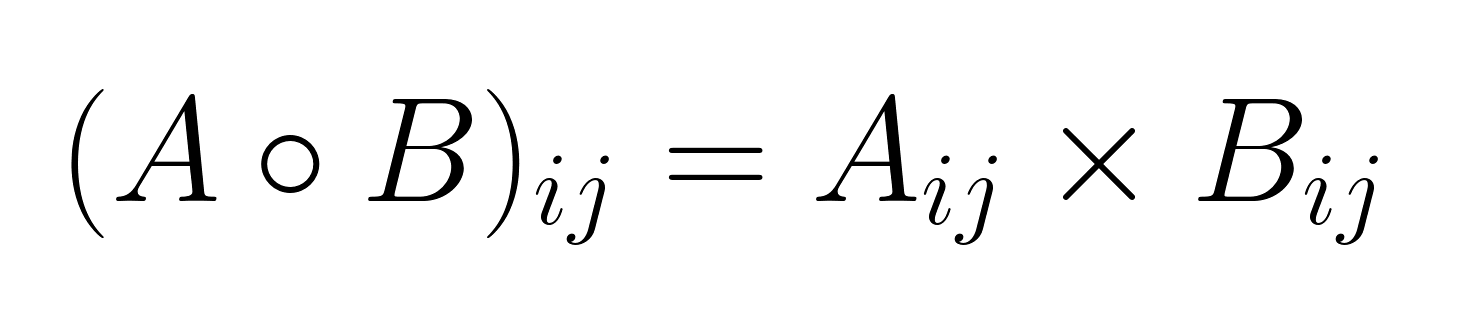
onde i varia de 1 a m e j vai de 1 a n.

A matriz que dá no final é C = A ∘ B tem as mesmas dimensões das matrizes de entrada, com cada elemento calculado de forma independente dos outros.

Notação padrão e convenções

Tem várias convenções de notação pro produto de Hadamard:

• (ponto vazio): A notação matemática mais comum
• (ponto circulado): Símbolo matemático alternativo
• .*: Usado em linguagens de programação como MATLAB.
• *: Operador de multiplicação por elemento em NumPy e outras bibliotecas

A escolha da notação geralmente depende do contexto e da área de aplicação, embora ∘ continua sendo o padrão na literatura matemática.

Exemplo passo a passo

Vamos ver o produto de Hadamard com um exemplo concreto usando duas matrizes 3×2:

Matrix A:

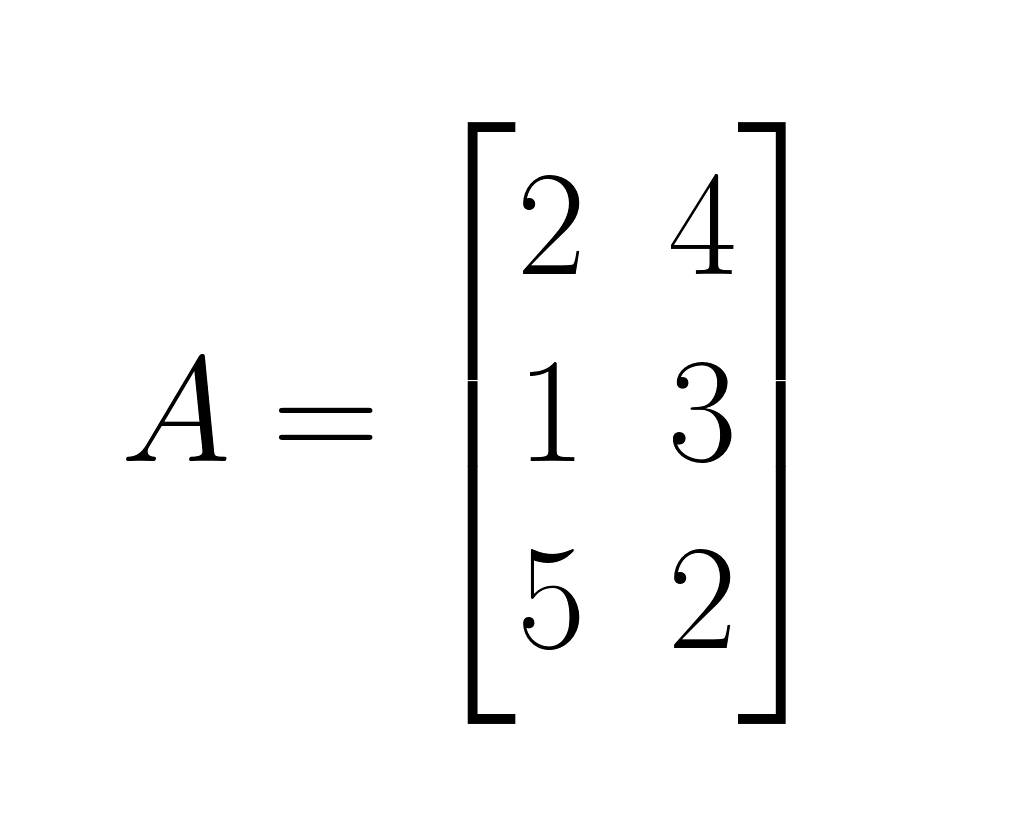
Matriz B:

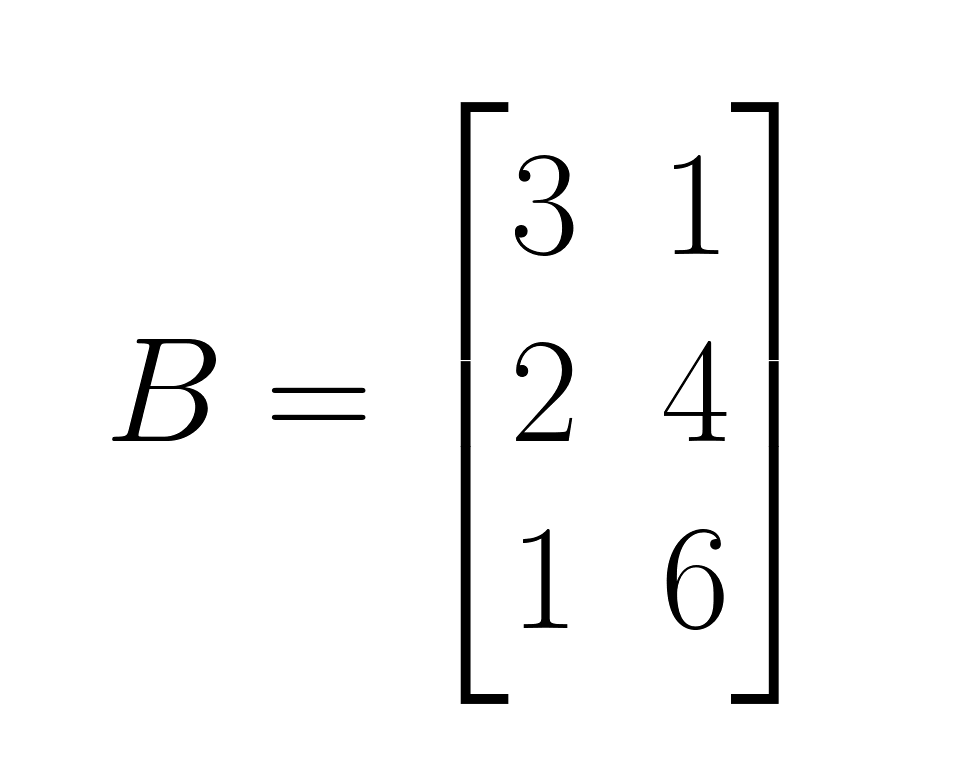
A ∘ B:

• Passo 1: Multiplica os elementos correspondentes na posição (1,1): 2 × 3 = 6 
• Passo 2: Multiplica os elementos correspondentes na posição (1,2): 4 × 1 = 4 
• Passo 3: Multiplica os elementos correspondentes na posição (2,1): 1 × 2 = 2 
• Passo 4: Multiplica os elementos correspondentes na posição (2,2): 3 × 4 = 12 
• Passo 5: Multiplica os elementos correspondentes na posição (3,1): 5 × 1 = 5 
• Passo 6: Multiplica os elementos correspondentes na posição (3,2): 2 × 6 = 12

E aí tá o resultado:

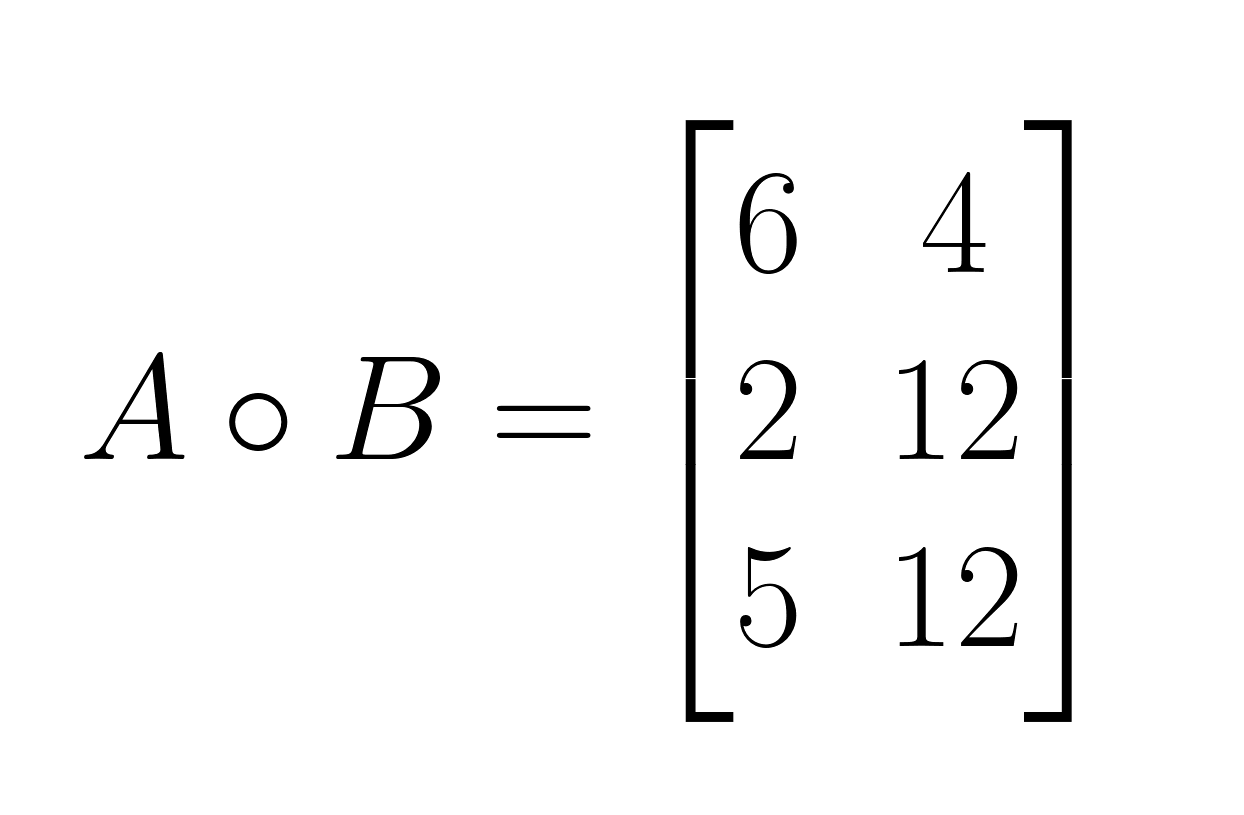
Restrições importantes

O produto de Hadamard tem um requisito dimensional bem rígido: as duas matrizes precisam ter dimensões iguais. Diferente da multiplicação de matrizes padrão, onde as dimensões internas precisam ser iguais, o produto de Hadamard exige que as dimensões sejam totalmente compatíveis. Essa restrição garante que cada elemento em uma matriz tenha um elemento correspondente na outra matriz para a multiplicação. Quando as matrizes têm dimensões diferentes, o produto de Hadamard não é definido.

Propriedades fundamentais e avançadas

O produto de Hadamard tem propriedades algébricas diferentes que o fazem ser diferente da multiplicação de matrizes padrão. Entender essas propriedades mostra por que a multiplicação elemento a elemento funciona de forma diferente e dá uma ideia da sua estrutura matemática.

Propriedades básicas

Comutatividade

O produto de Hadamard é comutativo, o que significa que a ordem da multiplicação não afeta o resultado:

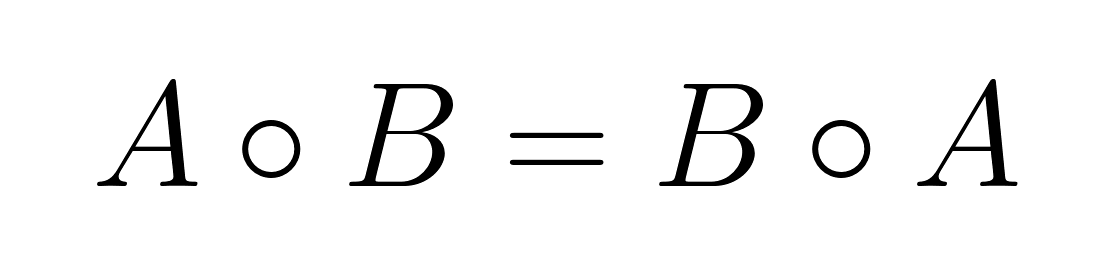
Essa propriedade vale porque a multiplicação elemento a elemento de números reais é comutativa: aᵢⱼ × bᵢⱼ = bᵢⱼ × aᵢⱼ.

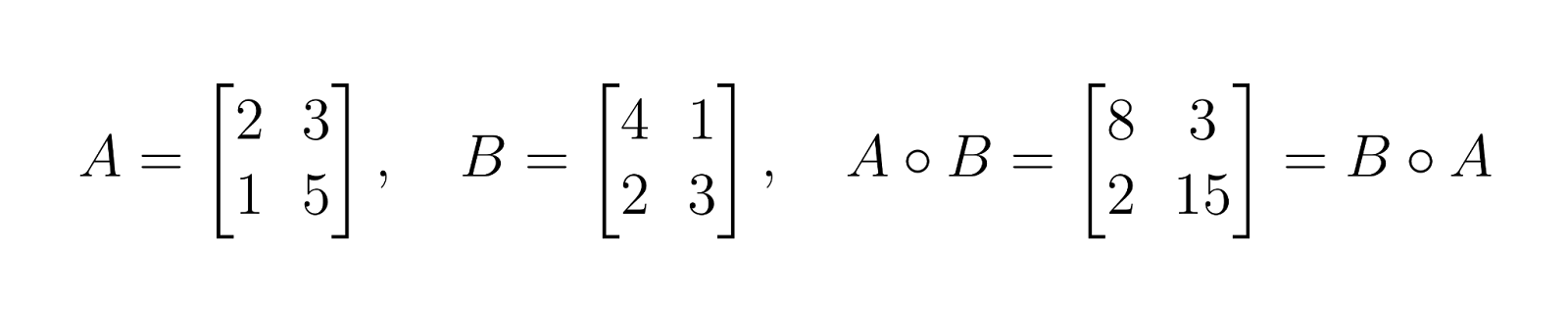
Isso é diferente da multiplicação de matrizes, que geralmente não é comutativa.

Associatividade

O produto de Hadamard é associativo, o que permite agrupar operações sem alterar o resultado:

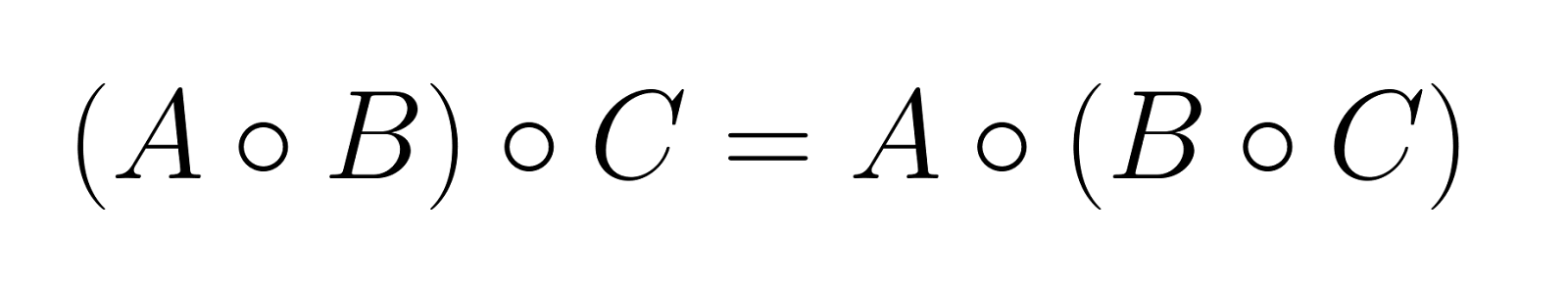
Essa propriedade vale para quantas matrizes você quiser, desde que todas tenham as mesmas dimensões.

Distributividade com adição de matrizes

O produto de Hadamard distribui-se pela soma das matrizes:

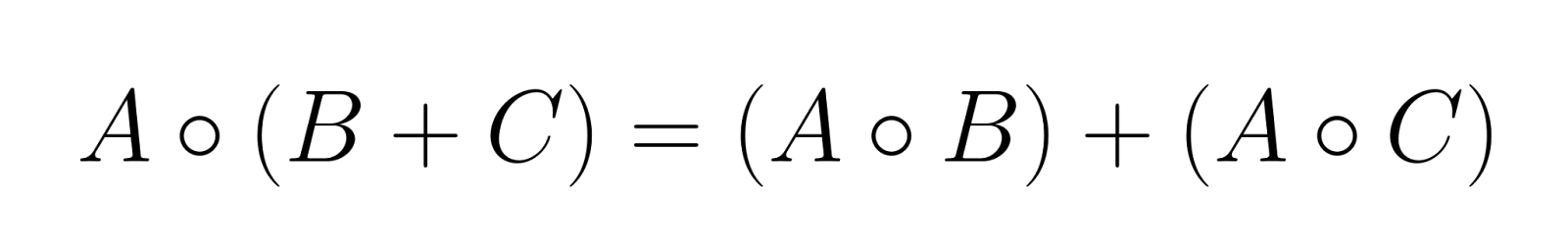
Essa propriedade faz com que o produto de Hadamard seja compatível com combinações lineares de matrizes.

Elemento de identidade

O elemento identidade para o produto de Hadamard é a matriz de todos os uns, J, onde cada elemento é igual a 1. Para qualquer matriz e A:

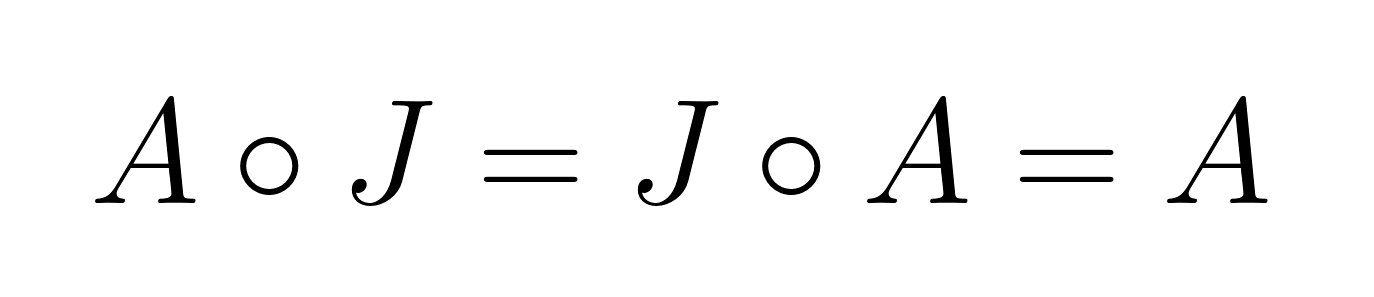
Isso é bem diferente da multiplicação de matrizes padrão, onde a matriz identidade tem uns na diagonal e zeros em todos os outros lugares.

Comparando com a multiplicação de matrizes padrão

Diferente da multiplicação de matrizes padrão, o produto de Hadamard:

• Precisa de matrizes com as mesmas dimensões.
• Produz um resultado com as mesmas dimensões das matrizes de entrada.
• É sempre comutativo
• Tem um elemento de identidade diferente
• Não satisfaz a propriedade associativa mista: (AB) ∘ C ≠ A(B ∘ C) em geral

A propriedade de produto misto

A propriedade do produto misto estabelece uma relação entre o produto de Hadamard e a transposição de matrizes:

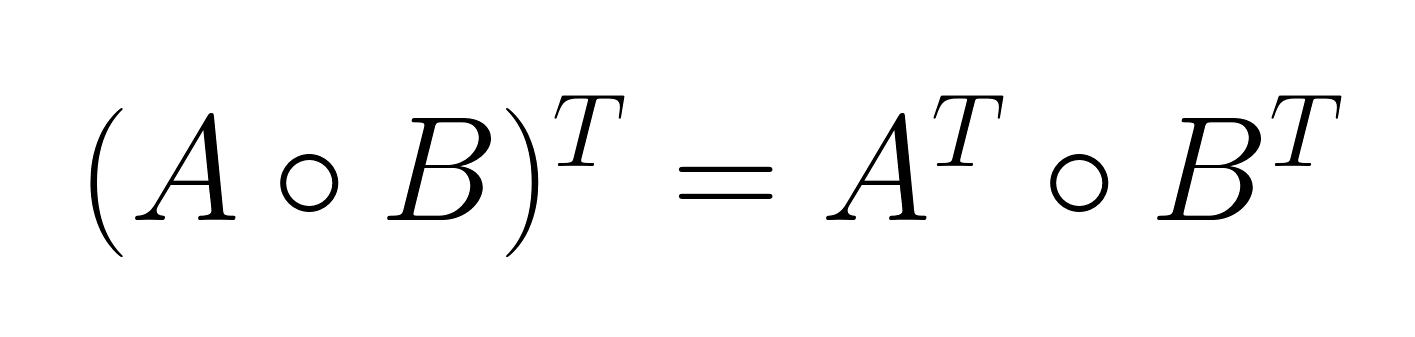
Essa propriedade é super útil em problemas de otimização e aplicações estatísticas, onde matrizes transpostas aparecem com frequência.

Aqui vai um exemplo: Na estimativa da matriz de covariância, os pesquisadores geralmente trabalham com matrizes de dados transpostas. A propriedade de produto misto permite que operações por elemento sejam feitas antes ou depois da transposição, dando flexibilidade computacional no design do algoritmo.

Teorema do produto de Schur e semidefinitividade positiva

O Teorema do Produto de Schur é um dos resultados teóricos mais importantes sobre o produto de Hadamard. Diz que o produto de Hadamard de duas matrizes semidefinidas positivas também é semidefinido positivo.

Teorema: Se A e B são matrizes semidefinidas positivas do mesmo tamanho, então A ∘ B é semidefinida positiva.

O que isso quer dizer para a análise de matriz

Esse teorema tem várias consequências importantes:

• Preservando a semidefinitividade positiva: A propriedade garante que certas operações matriciais mantenham propriedades matemáticas desejáveis. Na modelagem estatística, matrizes semidefinidas positivas representam estruturas de covariância válidas, e o teorema garante que a multiplicação elemento a elemento mantém essa validade.
• Conexão com a classificação da matriz: O produto de Hadamard geralmente não mantém a classificação da matriz. A classificação deum A ∘ B pode ser menor, igual ou (em casos especiais) maior que o mínimo de rank(A) e rank(B).
• Relações entre valores próprios: Embora o produto de Hadamard não tenha uma relação simples com os autovalores das matrizes originais, o Teorema do Produto de Schur fornece limites para os autovalores do resultado quando se trata de matrizes semidefinidas positivas.

Cálculo e implementação

As características computacionais do produto Hadamard o tornam especialmente legal para aplicações de processamento de dados em grande escala. Entender o perfil de eficiência e as considerações de implementação ajuda a otimizar o desempenho em ambientes de computação.

Eficiência e complexidade computacional

Análise de complexidade

O produto de Hadamard tem uma complexidade temporal de O(mn) para duas matrizes de tamanho m × n, onde cada elemento precisa de exatamente uma operação de multiplicação. Essa complexidade linear é bem diferente da multiplicação de matrizes padrão, que tem uma complexidade de O(n³) para matrizes quadradas usandoalgoritmos convencionais.

O que isso significa para o processamento em grande escala

A complexidade linear torna o produto de Hadamard especialmente bom para:

• Conjuntos de dados de alta dimensão: Quando você trabalha com matrizes com milhões de elementos, a complexidade O(mn) garante que o tempo de processamento seja proporcional ao tamanho dos dados.
• Aplicações em tempo real: A sobrecarga computacional mínima permite operações por elemento em cenários sensíveis ao tempo, como pipelines de processamento de imagens e inferência de redes neurais.
• Eficiência da memória: Como cada elemento é processado de forma independente, as implementações podem usar streaming ou processamento em blocos para lidar com conjuntos de dados maiores do que a memória disponível.

Multiplicação elemento a elemento na prática

Considerações sobre o processamento matricial

Calcular o produto de Hadamard envolve várias considerações práticas:

• Layout da memória: O armazenamento por linha versus coluna afeta o desempenho do cache. A maioria das implementações se beneficia do processamento dos elementos na mesma ordem em que aparecem na memória.
• Vetorização: Os processadores modernos suportam operações SIMD (instrução única, dados múltiplos) que podem processar vários elementos ao mesmo tempo, acelerando bastante a computação.
• Paralelização: A independência das operações por elemento torna o produto de Hadamard altamente paralelizável em vários núcleos de CPU ou threads de GPU.

Contextos e desafios do tensor

Quando a gente estende para tensores de dimensões mais altas, surgem complexidades adicionais:

• Transmissão: Muitas implementações suportam transmissão, permitindo a multiplicação elemento a elemento entre tensores de formas diferentes, mas compatíveis.
• Alinhamento da memória: As operações tensoriais exigem muita atenção ao alinhamento da memória para maximizar o desempenho, principalmente em hardware especializado, como GPUs e TPUs.
• Otimização do algoritmo: Algoritmos avançados como HaTT (Transformação de Hadamard para Tensores) oferecem implementações otimizadas para estruturas tensoriais específicas, reduzindo a complexidade de tempo e espaço em certos cenários.

Implementação em linguagens de programação

Python com NumPy

O NumPy oferece uma implementação direta do produto de Hadamard usando o operador *:

import numpy as np

# Define matrices
A = np.array([[2, 4], [1, 3], [5, 2]])
B = np.array([[3, 1], [2, 4], [1, 6]])

# Compute Hadamard product
C = A * B
print(C)
# Output: [[ 6  4]
#          [ 2 12]
#          [ 5 12]]

# Alternative explicit notation
C_explicit = np.multiply(A, B)

Otimização de desempenho no NumPy:

# For large matrices, ensure proper data types
A = A.astype(np.float32)  # Use float32 for memory efficiency
B = B.astype(np.float32)

# Pre-allocate output array for memory efficiency
C = np.empty_like(A)
np.multiply(A, B, out=C)

Idiomas e bibliotecas alternativos

R:

# C <- A * B  # Element-wise multiplication is default

matrix1 <- matrix(
  c(1, 2, 3,
    4, 5, 6,
    7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)

# Create the second matrix (3x3)
matrix2 <- matrix(
  c(9, 8, 7,
    6, 5, 4,
    3, 2, 1),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)

matrix1
matrix2
matrix1 * matrix2

     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6
[3,]    7    8    9
     [,1] [,2] [,3]
[1,]    9    8    7
[2,]    6    5    4
[3,]    3    2    1
     [,1] [,2] [,3]
[1,]    9   16   21
[2,]   24   25   24
[3,]   21   16    9

Julia:

C = A .* B  # Broadcasting element-wise multiplication	

Erros comuns e melhores práticas

Compatibilidade de tipos: Garanta que as matrizes tenham tipos de dados compatíveis para evitar promoção de tipos inesperada ou perda de precisão.

# Avoid mixing integer and float types unnecessarily
A = np.array([[1, 2]], dtype=np.int32)
B = np.array([[1.5, 2.5]], dtype=np.float64)
C = A * B  # Results in float64, may not be intended

Divulgação da conscientização: Entenda como funciona a transmissão para evitar que as dimensões aumentem sem querer.

# Be explicit about intended operations
A = np.array([[1, 2, 3]])      # Shape: (1, 3)
B = np.array([[1], [2], [3]])  # Shape: (3, 1)
C = A * B  # Results in (3, 3) matrix due to broadcasting

Gerenciamento de memória: Para operações em grande escala, considere operações no local e pré-alocação de memória.

# In-place operation to save memory
A *= B  # Modifies A directly

# Pre-allocate for repeated operations
result = np.empty((1000, 1000))
for i in range(iterations):
    np.multiply(matrix1, matrix2, out=result)

Integração de pipeline: Em fluxos de trabalho de machine learning, certifique-se de que as operações Hadamard se integram perfeitamente com estruturas de diferenciação automática e mantêm o fluxo de gradiente.

Aplicações em várias áreas

O produto de Hadamard é usado em operações que precisam de transformações localizadas, mas sem perder a estrutura da matriz.

Processamento de imagens

O produto Hadamard é super importante na decodificação JPEG, onde junta matrizes de quantização com coeficientes de imagem transformados para reconstruir dados visuais. Em tarefas de aprimoramento de imagem, permite operações seletivas, como supressão de ruído por meio da multiplicação por elemento com máscaras de filtro e nitidez ou desfoque controlados, aplicando matrizes de peso espacial às vizinhanças dos pixels.

Modelagem estatística e análise de dados

O produto Hadamard facilita a regressão ponderada aplicando pesos por elemento às matrizes de projeto e dá suporte à estimativa robusta de covariância por meio do dimensionamento seletivo dos elementos da matriz. A operação é essencial em métodos de kernel e programação semidefinida, onde ela mantém a propriedade semidefinida positiva necessária para modelos estatísticos válidos, tornando-a valiosa para técnicas de regularização que aplicam restrições por elemento a estruturas de covariância.

Aprendizado profundo e redes neurais

O produto Hadamard aparece bastante em arquiteturas de redes neurais recorrentes, principalmente em GRUs e LSTMs, onde controla o fluxo de informações por meio de mecanismos de gate elementar. Arquiteturas modernas como StyleGAN e SENet usam isso pra escalonamento adaptativo de recursos, enquanto mecanismos de atenção usam multiplicação por elemento pra ponderar representações de recursos, melhorando bastante a eficiência e o desempenho do modelo em modelagem de sequências e tarefas generativas.

Outras aplicações importantes

O produto de Hadamard se estende ao processamento de sinais para filtragem no domínio da frequência e análise espectral, onde a multiplicação elemento a elemento com funções de transferência modifica as características do sinal. Na teoria dos grafos, permite operações por vértice em matrizes de adjacência, enquanto as aplicações combinatórias incluem a manipulação por elemento de matrizes de contagem e problemas de otimização discreta.

Conclusão

Se você quiser saber mais sobre os conceitos matemáticos que estão por trás do machine learning e do deep learning modernos, nosso tutorial Desmistificando conceitos matemáticos para deep learning traz mais informações sobre as bases matemáticas que impulsionam as inovações atuais em IA. E, se quiser uma base sólida, inscreva-se no nosso curso Álgebra linear para ciência de dados em R.