Producto de Hadamard: Guía completa sobre la multiplicación de matrices elemento por elemento

Este tutorial explora los fundamentos matemáticos, las características computacionales y las amplias aplicaciones del producto de Hadamard. A través de ejemplos prácticos, descubrirás cómo esta operación une las matemáticas teóricas con las aplicaciones de la ciencia de datos, lo que la convierte en una herramienta esencial para cualquiera que trabaje con matrices y datos de alta dimensión.

Para sentar unas bases sólidas en operaciones matriciales, explora nuestro curso Álgebra lineal para ciencia de datos en R, que abarca conceptos esenciales que complementan el producto de Hadamard. 

Definición y notación matemática

El producto de Hadamard, también conocido como multiplicación por elementos, representa una de las operaciones más versátiles del álgebra matricial. A diferencia de la multiplicación de matrices estándar, esta operación combina matrices multiplicando los elementos correspondientes, creando resultados que conservan las dimensiones originales y permiten transformaciones localizadas.

Definición formal

Dadas dos matrices A y B, ambas de tamaño m × n, su producto de Hadamard A ∘ B (o a veces denotado como A ⊙ B) se calcula multiplicando los elementos correspondientes:

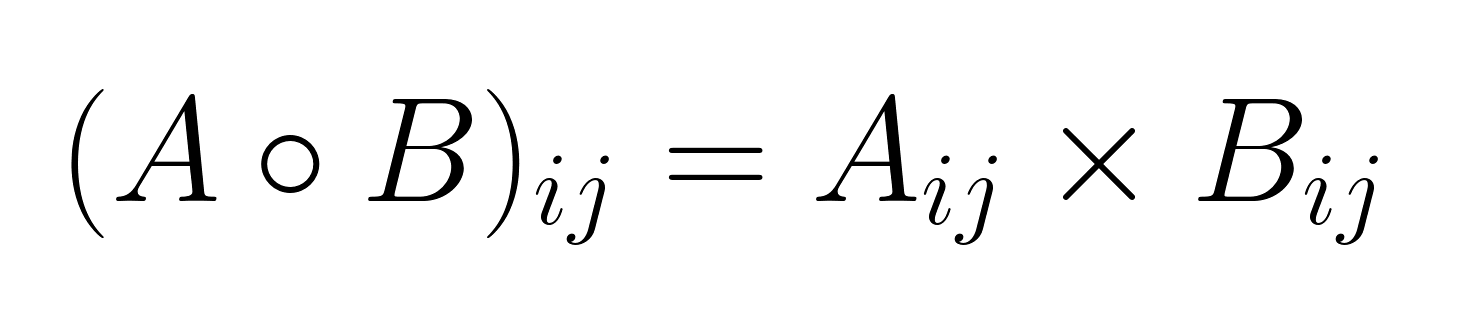
donde i varía de 1 a m y j varía de 1 a n.

La matriz resultante C = A ∘ B tiene las mismas dimensiones que las matrices de entrada, y cada elemento se calcula independientemente de los demás.

Notación estándar y convenciones

Existen varias convenciones notacionales para el producto de Hadamard:

• (punto hueco): La notación matemática más común
• (punto rodeado por un círculo): Símbolo matemático alternativo
• .*: Se utiliza en lenguajes de programación como MATLAB.
• *: Operador de multiplicación por elementos en NumPy y otras bibliotecas

La elección de la notación suele depender del contexto y del campo de aplicación, aunque ∘ sigue siendo el estándar en la literatura matemática.

Ejemplo paso a paso

Ilustremos el producto de Hadamard con un ejemplo concreto utilizando dos matrices de 3×2:

Matriz A:

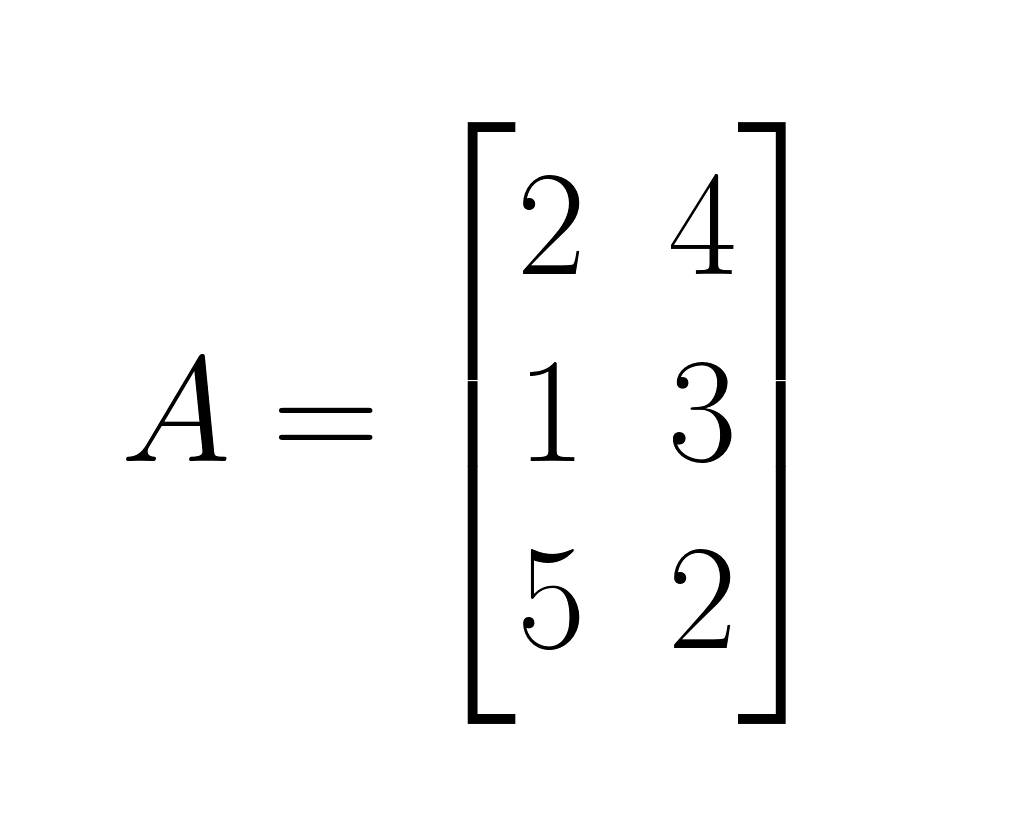
Matriz B:

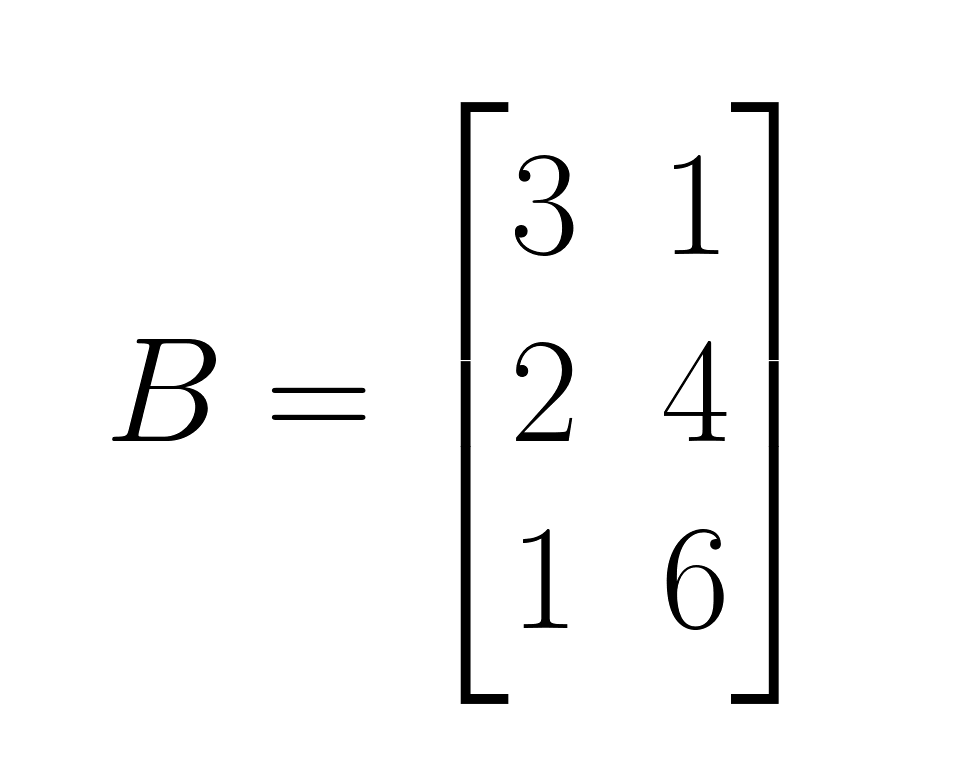
A ∘ B:

• Paso 1: Multiplica los elementos correspondientes en la posición (1,1): 2 × 3 = 6 
• Paso 2: Multiplica los elementos correspondientes en la posición (1,2): 4 × 1 = 4 
• Paso 3: Multiplica los elementos correspondientes en la posición (2,1): 1 × 2 = 2 
• Paso 4: Multiplica los elementos correspondientes en la posición (2,2): 3 × 4 = 12 
• Paso 5: Multiplica los elementos correspondientes en la posición (3,1): 5 × 1 = 5 
• Paso 6: Multiplica los elementos correspondientes en la posición (3,2): 2 × 6 = 12

Este es el resultado:

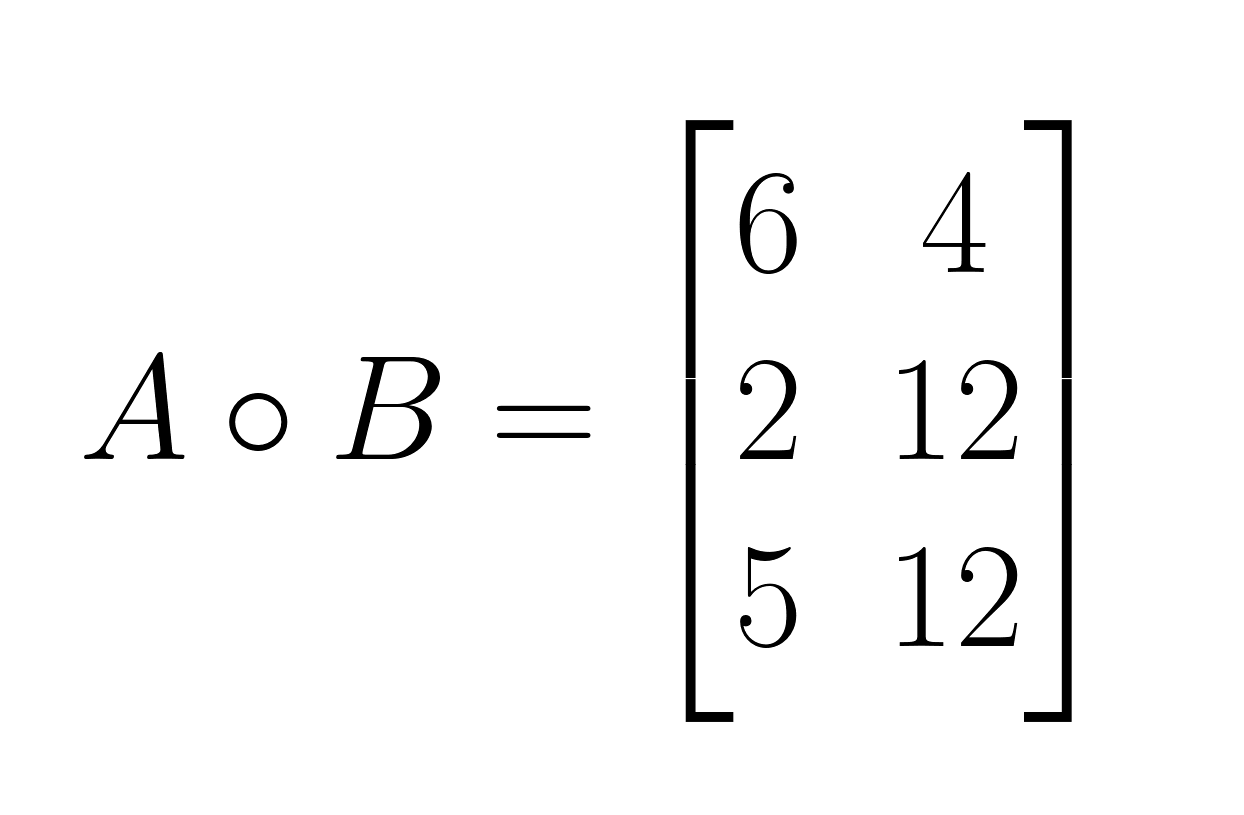
Restricciones importantes

El producto de Hadamard tiene un requisito dimensional estricto: ambas matrices deben tener dimensiones idénticas. A diferencia de la multiplicación matricial estándar, en la que las dimensiones internas deben coincidir, el producto de Hadamard requiere una compatibilidad dimensional completa. Esta restricción garantiza que cada elemento de una matriz tenga un elemento correspondiente en la otra matriz para la multiplicación. Cuando las matrices tienen dimensiones diferentes, el producto de Hadamard no está definido.

Propiedades fundamentales y avanzadas

El producto de Hadamard presenta propiedades algebraicas distintivas que lo diferencian de la multiplicación matricial estándar. Comprender estas propiedades revela por qué la multiplicación por elementos se comporta de manera diferente y proporciona información sobre su estructura matemática.

Propiedades básicas

Conmutatividad

El producto de Hadamard es conmutativo, lo que significa que el orden de la multiplicación no afecta al resultado:

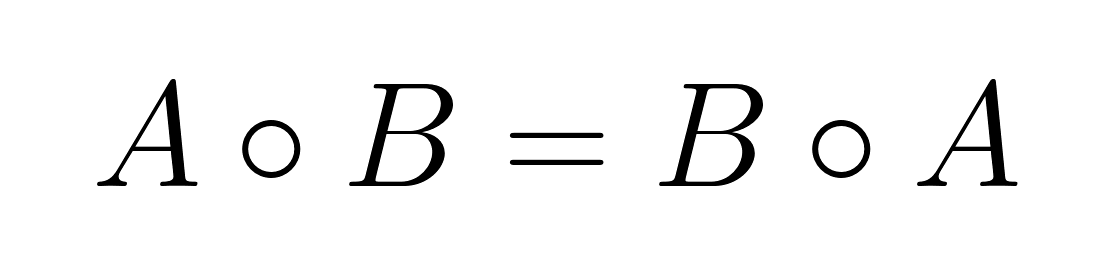
Esta propiedad se cumple porque la multiplicación elemento por elemento de números reales es conmutativa: aᵢⱼ × bᵢⱼ = bᵢⱼ × aᵢⱼ.

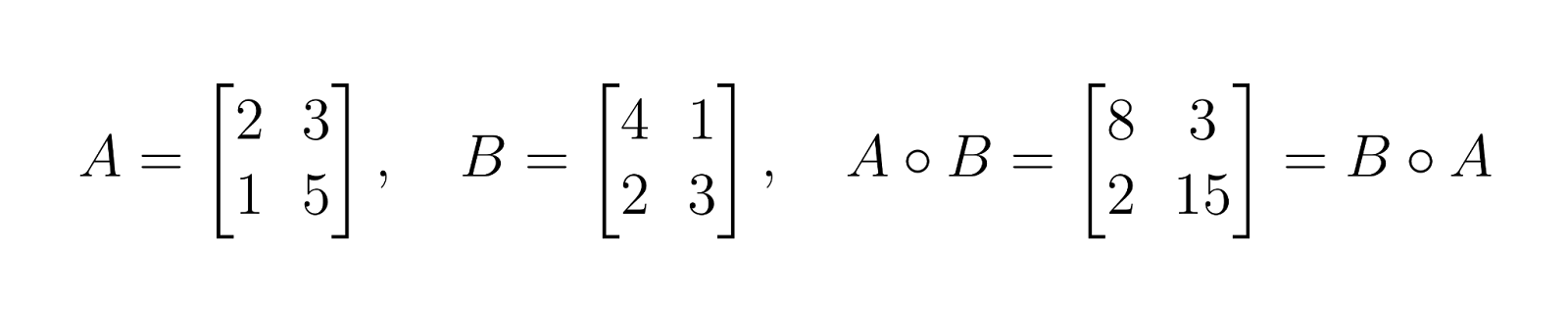
Esto es diferente a la multiplicación de matrices, que generalmente no es conmutativa.

Asociatividad

El producto de Hadamard es asociativo, lo que permite agrupar operaciones sin cambiar el resultado:

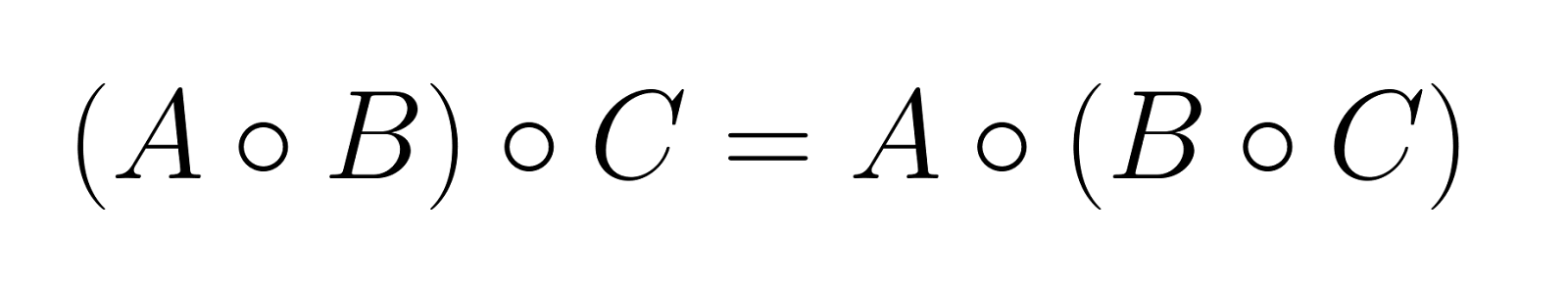
Esta propiedad se extiende a cualquier número de matrices, siempre que todas tengan dimensiones idénticas.

Distributividad con suma de matrices

El producto de Hadamard se distribuye sobre la suma de matrices:

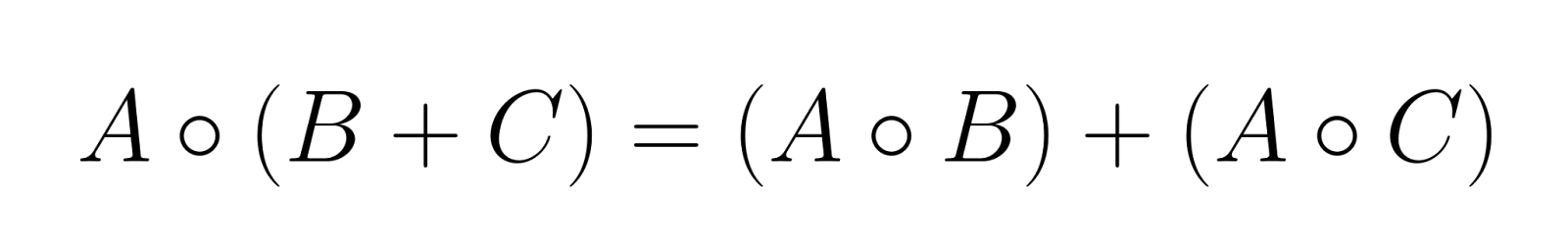
Esta propiedad hace que el producto de Hadamard sea compatible con combinaciones lineales de matrices.

Elemento de identidad

El elemento identidad para el producto de Hadamard es la matriz de todos los unos, J, donde todos los elementos son iguales a 1. Para cualquier matrize a A:

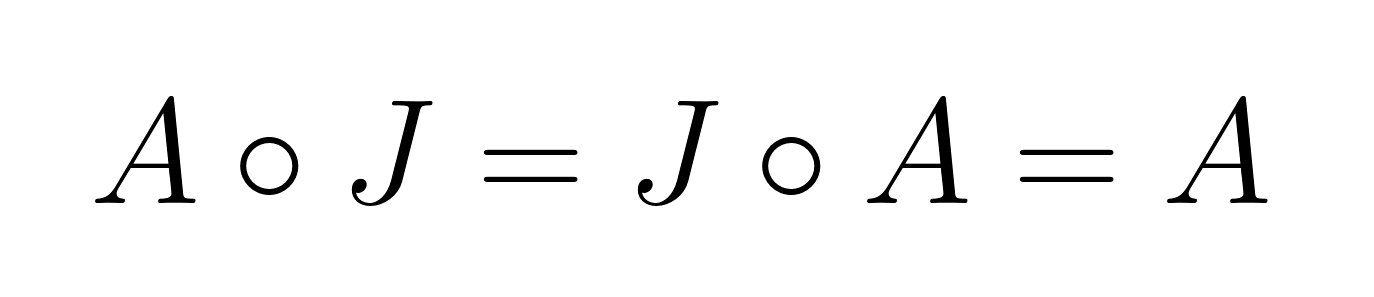
Esto difiere significativamente de la multiplicación matricial estándar, donde la matriz identidad tiene unos en la diagonal y ceros en el resto de casillas.

Comparación con la multiplicación matricial estándar

A diferencia de la multiplicación matricial estándar, el producto de Hadamard:

• Requiere matrices de dimensiones idénticas.
• Produce un resultado con las mismas dimensiones que las matrices de entrada.
• Siempre es conmutativo.
• Tiene un elemento de identidad diferente.
• No satisface la propiedad asociativa mixta: (AB) ∘ C ≠ A(B ∘ C) en general

La propiedad de productos mixtos

La propiedad de producto mixto establece una relación entre el producto de Hadamard y la transposición de matrices:

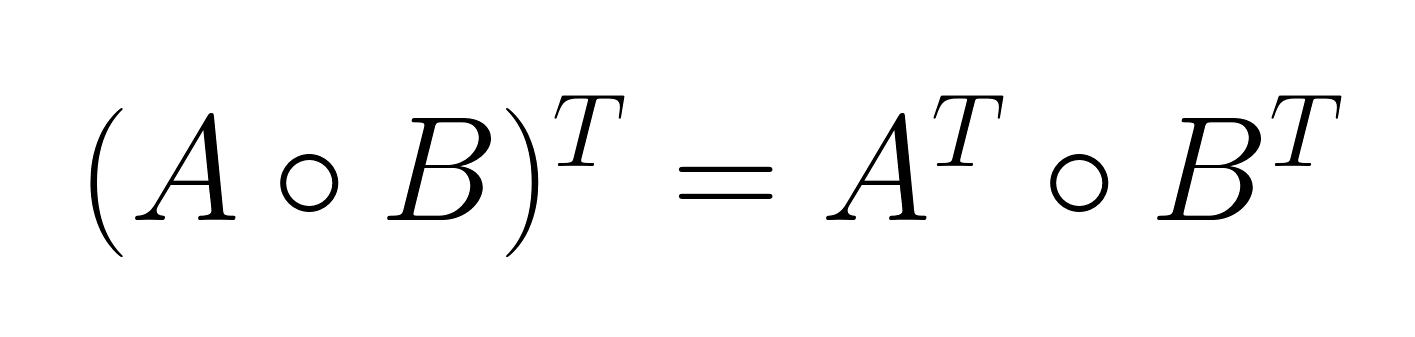
Esta propiedad resulta especialmente útil en problemas de optimización y aplicaciones estadísticas en los que aparecen con frecuencia matrices transpuestas.

xHe aquí un ejemplo: En la estimación de la matriz de covarianza, los investigadores suelen trabajar con matrices de datos transpuestas. La propiedad de producto mixto permite realizar operaciones por elementos antes o después de la transposición, lo que proporciona flexibilidad computacional en el diseño de algoritmos.

Teorema de Schur y semidefinición positiva

El teorema del producto de Schur representa uno de los resultados teóricos más significativos en relación con el producto de Hadamard. Afirma que el producto de Hadamard de dos matrices semidefinidas positivas también es semidefinido positivo.

Teorema: Si A y B son matrices semidefinidas positivas del mismo tamaño, entonces A ∘ B es semidefinida positiva.

Implicaciones para el análisis matricial

Este teorema tiene varias consecuencias importantes:

• Preservar la semidefinición positiva: La propiedad garantiza que determinadas operaciones matriciales mantengan las propiedades matemáticas deseadas. En el modelado estadístico, las matrices semidefinidas positivas representan estructuras de covarianza válidas, y el teorema garantiza que la multiplicación elemento por elemento conserva esta validez.
• Relación con el rango de la matriz: El producto de Hadamard generalmente no conserva el rango de la matriz. El rango de A ∘ B puede ser menor, igual o (en casos especiales) mayor que el mínimo de rank(A) y rank(B).
• Relaciones entre valores propios: Si bien el producto de Hadamard no tiene una relación simple con los valores propios de las matrices originales, el teorema del producto de Schur proporciona límites para los valores propios del resultado cuando se trata de matrices semidefinidas positivas.

Cálculo e implementación

Las características computacionales del producto de Hadamard lo hacen especialmente atractivo para aplicaciones de procesamiento de datos a gran escala. Comprender su perfil de eficiencia y las consideraciones de implementación ayuda a optimizar el rendimiento en entornos informáticos.

Eficiencia y complejidad computacional

Análisis de complejidad

El producto de Hadamard tiene una complejidad temporal de O(mn) para dos matrices de tamaño m × n, donde cada elemento requiere exactamente una operación de multiplicación. Esta complejidad lineal contrasta fuertemente con la multiplicación matricial estándar, que tiene una complejidad de O(n³) para matrices cuadradas utilizandoalgoritmos convencionales.

Implicaciones para el procesamiento a gran escala

La complejidad lineal hace que el producto de Hadamard sea especialmente adecuado para:

• Conjuntos de datos de alta dimensión: Cuando se trabaja con matrices que contienen millones de elementos, la complejidad O(mn) garantiza que los tiempos de procesamiento se escalan de forma predecible con el tamaño de los datos.
• Aplicaciones en tiempo real: La mínima sobrecarga computacional permite operaciones por elementos en escenarios sensibles al tiempo, como los procesos de procesamiento de imágenes y la inferencia de redes neuronales.
• Eficiencia de la memoria: Dado que cada elemento se procesa de forma independiente, las implementaciones pueden aprovechar el procesamiento por secuencias o por bloques para gestionar conjuntos de datos más grandes que la memoria disponible.

Multiplicación por elementos en la práctica

Consideraciones sobre el procesamiento matricial

El cálculo del producto de Hadamard implica varias consideraciones prácticas:

• Disposición de la memoria: El almacenamiento por filas frente al almacenamiento por columnas afecta al rendimiento de la caché. La mayoría de las implementaciones se benefician de procesar los elementos en el mismo orden en que aparecen en la memoria.
• Vectorización: Los procesadores modernos admiten operaciones SIMD (instrucción única, datos múltiples) que pueden procesar varios elementos simultáneamente, lo que acelera considerablemente el cálculo.
• Paralelización: La independencia de las operaciones por elementos hace que el producto de Hadamard sea altamente paralelizable en múltiples núcleos de CPU o subprocesos de GPU.

Contextos tensores y retos

Al extenderlo a tensores de dimensiones superiores, surgen complejidades adicionales:

• Difusión: Muchas implementaciones admiten la difusión, lo que permite la multiplicación por elementos entre tensores de formas diferentes pero compatibles.
• Alineación de la memoria: Las operaciones tensoriales requieren prestar especial atención a la alineación de la memoria para maximizar el rendimiento, especialmente en hardware especializado como GPU y TPU.
• Optimización del algoritmo: Los algoritmos avanzados como HaTT (Hadamard Transform for Tensors) proporcionan implementaciones optimizadas para estructuras tensoriales específicas, lo que reduce tanto la complejidad temporal como la espacial en determinados escenarios.

Implementación en lenguajes de programación

Python con NumPy

NumPy proporciona una implementación sencilla del producto de Hadamard utilizando el operador *:

import numpy as np

# Define matrices
A = np.array([[2, 4], [1, 3], [5, 2]])
B = np.array([[3, 1], [2, 4], [1, 6]])

# Compute Hadamard product
C = A * B
print(C)
# Output: [[ 6  4]
#          [ 2 12]
#          [ 5 12]]

# Alternative explicit notation
C_explicit = np.multiply(A, B)

Optimización del rendimiento en NumPy:

# For large matrices, ensure proper data types
A = A.astype(np.float32)  # Use float32 for memory efficiency
B = B.astype(np.float32)

# Pre-allocate output array for memory efficiency
C = np.empty_like(A)
np.multiply(A, B, out=C)

Idiomas y bibliotecas alternativos

R:

# C <- A * B  # Element-wise multiplication is default

matrix1 <- matrix(
  c(1, 2, 3,
    4, 5, 6,
    7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)

# Create the second matrix (3x3)
matrix2 <- matrix(
  c(9, 8, 7,
    6, 5, 4,
    3, 2, 1),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)

matrix1
matrix2
matrix1 * matrix2

     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6
[3,]    7    8    9
     [,1] [,2] [,3]
[1,]    9    8    7
[2,]    6    5    4
[3,]    3    2    1
     [,1] [,2] [,3]
[1,]    9   16   21
[2,]   24   25   24
[3,]   21   16    9

Julia:

C = A .* B  # Broadcasting element-wise multiplication	

Errores comunes y mejores prácticas

Compatibilidad de tipos: Asegúrate de que las matrices tengan tipos de datos compatibles para evitar promociones de tipos inesperadas o pérdidas de precisión.

# Avoid mixing integer and float types unnecessarily
A = np.array([[1, 2]], dtype=np.int32)
B = np.array([[1.5, 2.5]], dtype=np.float64)
C = A * B  # Results in float64, may not be intended

Difusión de la concienciación: Comprende cómo funciona la difusión para evitar la expansión involuntaria de dimensiones.

# Be explicit about intended operations
A = np.array([[1, 2, 3]])      # Shape: (1, 3)
B = np.array([[1], [2], [3]])  # Shape: (3, 1)
C = A * B  # Results in (3, 3) matrix due to broadcasting

Gestión de la memoria: Para operaciones a gran escala, considera las operaciones in situ y la preasignación de memoria.

# In-place operation to save memory
A *= B  # Modifies A directly

# Pre-allocate for repeated operations
result = np.empty((1000, 1000))
for i in range(iterations):
    np.multiply(matrix1, matrix2, out=result)

Integración de tuberías: En los flujos de trabajo de machine learning, asegúrate de que las operaciones de Hadamard se integren perfectamente con los marcos de diferenciación automática y mantengan el flujo de gradientes.

Aplicaciones en diversas disciplinas

El producto de Hadamard se utiliza en operaciones que requieren transformaciones localizadas conservando la estructura de la matriz.

Procesamiento de imágenes

El producto de Hadamard desempeña un papel fundamental en la decodificación JPEG, donde combina matrices de cuantificación con coeficientes de imagen transformados para reconstruir datos visuales. En tareas de mejora de imágenes, permite operaciones selectivas como la supresión de ruido mediante la multiplicación por elementos con máscaras de filtro y el enfoque o desenfoque controlados mediante la aplicación de matrices de ponderación espacial a los píxeles vecinos.

Modelización estadística y análisis de datos

El producto Hadamard facilita la regresión ponderada mediante la aplicación de ponderaciones por elementos a las matrices de diseño y admite una estimación robusta de la covarianza mediante el escalado selectivo de los elementos de la matriz. La operación resulta esencial en los métodos del núcleo y la programación semidefinida, donde preserva la propiedad semidefinida positiva necesaria para los modelos estadísticos válidos, lo que la hace valiosa para las técnicas de regularización que aplican restricciones por elementos a las estructuras de covarianza.

Aprendizaje profundo y redes neuronales

El producto de Hadamard aparece ampliamente en arquitecturas de redes neuronales recurrentes, particularmente en GRU y LSTM, donde controla el flujo de información a través de mecanismos de activación por elementos. Las arquitecturas modernas como StyleGAN y SENet lo utilizan para el escalado adaptativo de características, mientras que los mecanismos de atención emplean la multiplicación por elementos para ponderar las representaciones de características, lo que mejora significativamente tanto la eficiencia como el rendimiento del modelo en el modelado de secuencias y en tareas generativas.

Otras aplicaciones destacadas

El producto de Hadamard se extiende al procesamiento de señales para el filtrado en el dominio de la frecuencia y el análisis espectral, donde la multiplicación elemento por elemento con funciones de transferencia modifica las características de la señal. En teoría de grafos, permite realizar operaciones por vértices en matrices de adyacencia, mientras que las aplicaciones combinatorias incluyen la manipulación por elementos de matrices de recuento y problemas de optimización discreta.

Conclusión

Si te interesa explorar más conceptos matemáticos que sustentan el machine learning y el deep learning modernos, nuestro tutorial Desmitificando los conceptos matemáticos para el deep learning proporciona información adicional sobre los fundamentos matemáticos que impulsan las innovaciones actuales en IA, y inscríbete en nuestro curso Álgebra lineal para la ciencia de datos en R para obtener una base sólida.