Kurs
Die lineare Regression ist eine der wichtigsten und grundlegendsten statistischen Techniken. Die Beherrschung dieser Technik ist für jeden Datenanalysten und Datenwissenschaftler unverzichtbar, denn sie bildet, wie du sehen wirst, die Grundlage für viele fortgeschrittenere Methoden.
Dieses Tutorial führt dich durch den Prozess der Durchführung einer linearen Regression in der wichtigen Programmiersprache R. Am Ende dieses Tutoriums wirst du verstehen, wie man lineare Regressionsmodelle implementiert und interpretiert, sodass du dieses Wissen leichter auf deine Datenanalyseaufgaben anwenden kannst.
Wenn du mit der Programmiersprache R noch nicht vertraut bist, empfehle ich dir unsere DataCamp-Tutorials für den Einstieg: Exploratory Data Analysis in R for Absolute Beginners und Mastering Data Structures in the R Programming Language.
Was ist lineare Regression?
Eine lineare Regression ist ein statistisches Modell, das die Beziehung zwischen einer Antwortvariablen (oft y genannt) und einer oder mehreren Variablen und ihren Wechselwirkungen (oft x oder erklärende Variablen genannt) analysiert. Du stellst diese Art von Beziehung ständig in deinem Kopf her. Wenn du zum Beispiel das Alter eines Kindes anhand seiner Größe berechnest, gehst du davon aus, dass es umso größer ist, je älter es ist.
Die lineare Regression ist eines der grundlegendsten statistischen Modelle, die es gibt. Ihre Ergebnisse können von fast jedem interpretiert werden, und es gibt sie schon seit dem 19. Das ist genau das, was die lineare Regression so beliebt macht. Es ist einfach und hat Hunderte von Jahren überlebt. Auch wenn sie nicht so ausgefeilt ist wie andere Algorithmen wie künstliche neuronale Netze oder Zufallswälder, war die Regression laut einer Umfrage von KD Nuggets der Algorithmus, der 2016 und 2017 von Datenwissenschaftlern am häufigsten verwendet wurde. Es wird sogar vorhergesagt, dass sie im Jahr 2118 noch benutzt wird!
In diesem Tutorium zur linearen Regression erfahren wir, wie du eine lineare Regression in R erstellst. Wir zeigen dir die Schritte, die du dafür brauchst, und ein Beispiel, das du durcharbeiten kannst.
Um den gesamten Beispielcode in diesem Tutorial einfach selbst auszuführen, kannst du eine kostenlose DataLab-Arbeitsmappe erstellen, auf der R vorinstalliert ist und die alle Codebeispiele enthält. Wenn du mehr über die lineare Regression erfahren möchtest, schau dir diese praktische DataCamp-Übung an.
Wie man eine lineare Regression in R erstellt
Nicht jedes Problem kann mit demselben Algorithmus gelöst werden. Eine lineare Regression ist bekanntlich gut, wenn es eine lineare Beziehung zwischen der Antwort und dem Ergebnis gibt. Mit anderen Worten: Die lineare Regression geht davon aus, dass eine lineare Beziehung zwischen der Antwortvariablen und den erklärenden Variablen besteht . Im Falle von zwei Variablen bedeutet das, dass du eine Linie zwischen den beiden Variablen einfügen kannst. Um noch einmal auf unser vorheriges Beispiel mit dem Alter des Kindes zurückzukommen: Es ist klar, dass es einen Zusammenhang zwischen dem Alter der Kinder und ihrer Größe gibt.
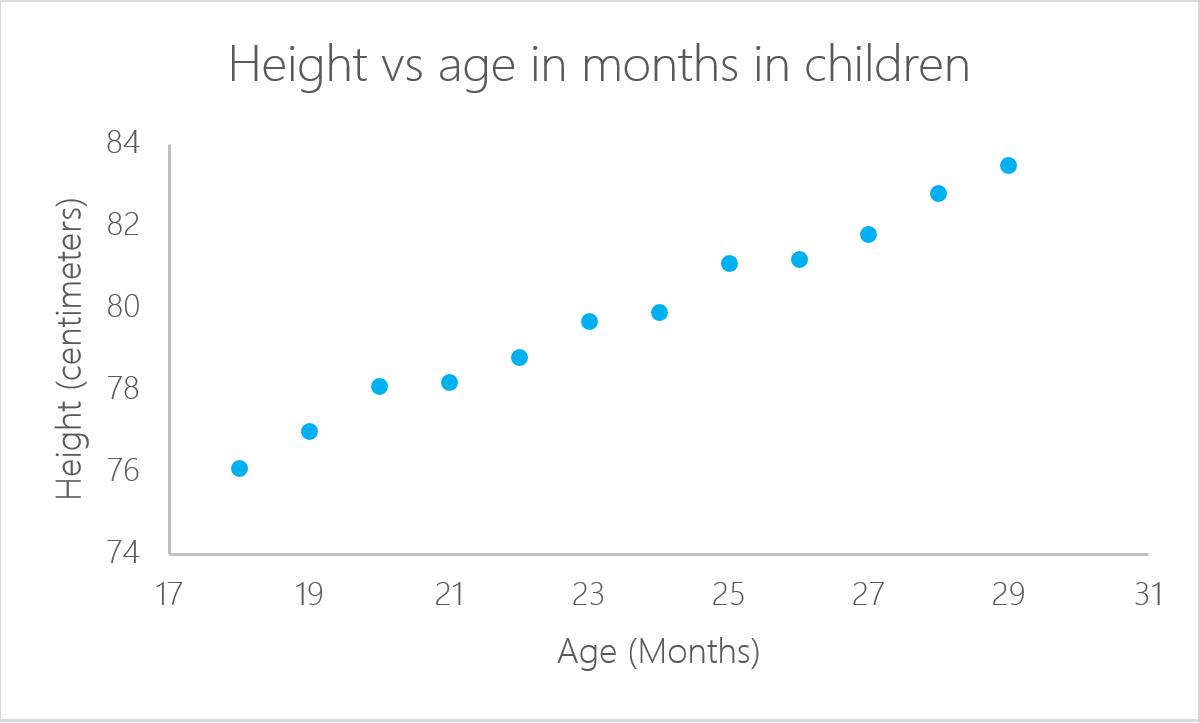
In diesem Beispiel kannst du die Größe eines Kindes berechnen, wenn du sein Alter kennst:
![]()
In diesem Fall sind a und b der Achsenabschnitt bzw. die Steigung. In demselben Beispiel ist a, der Achsenabschnitt, der Wert, bei dem du mit der Messung beginnst. Neugeborene Babys, die null Monate alt sind, sind nicht null Zentimeter groß. Dies ist die Funktion des Abschnitts. Die Steigung misst die Veränderung der Körpergröße im Verhältnis zum Alter in Monaten. Generell gilt: Mit jedem Monat, den das Kind älter ist, nimmt seine Größe mit b zu.
lm() in R
Eine lineare Regression kann in R mit dem Befehl lm() berechnet werden. Im nächsten Beispiel verwenden wir diesen Befehl, um die geschätzte Größe auf der Grundlage des Alters des Kindes zu berechnen.
Importiere zunächst die Bibliothek readxl, um Microsoft Excel-Dateien zu lesen. Unser Kurs Einführung in den Datenimport in R ist eine großartige Ressource, wenn du mit dem Import von Excel- oder CSV-Dateien in eine R-Umgebung wie RStudio nicht vertraut bist.
Du kannst die Daten für diesen Lehrgang herunterladen, bevor du loslegst. Lade die Daten in ein Objekt namens ageandheight herunter und erstelle dann die lineare Regression in der dritten Zeile. Die Funktion lm() nimmt die Variablen im Format:
lm([target] ~ [predictor], data = [data source])Im folgenden Code verwenden wir die Funktion lm(), um ein lineares Modellobjekt zu erstellen, das wir lmHeight nennen. Wir verwenden dann die Funktion summary() auf lmHeight, um detaillierte Informationen über die Leistung und die Koeffizienten des Modells zu erhalten.
library(readxl)
ageandheight <- read_excel("ageandheight.xls", sheet = "Hoja2") #Upload the data
lmHeight = lm(height~age, data = ageandheight) #Create the linear regression
summary(lmHeight) #Review the resultsR für maschinelles Lernen lernen
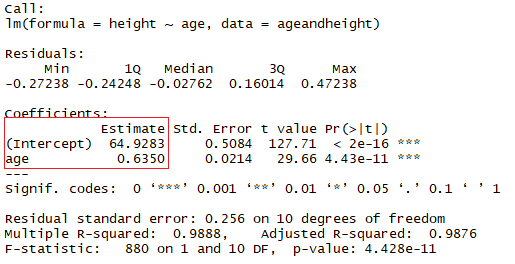
Was sind Koeffizienten?
Im roten Quadrat siehst du die Werte für den Achsenabschnitt ("a"-Wert) und die Steigung ("b"-Wert) für das Alter. Diese "a"- und "b"-Werte zeichnen eine Linie zwischen allen Punkten der Daten. Wenn also in diesem Fall ein Kind 20,5 Monate alt ist, a 64,92 und b 0,635 beträgt, sagt das Modell (im Durchschnitt) eine Körpergröße in Zentimetern von 64,92 + (0,635 * 20,5) = 77,93 cm voraus.
Wenn bei einer Regression zwei oder mehr Prädiktoren berücksichtigt werden, um die lineare Regression zu erstellen, spricht man von einer multiplen linearen Regression. Nach der gleichen Logik, die du in dem einfachen Beispiel zuvor verwendet hast, wird die Größe des Kindes mit gemessen:
Höhe = a + Alter × b1 + (Anzahl der Geschwister) × b2
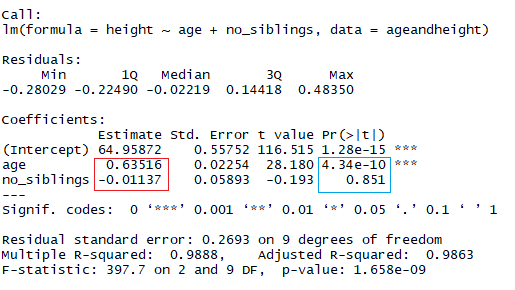
Du betrachtest jetzt die Größe als Funktion des Alters in Monaten und der Anzahl der Geschwister des Kindes. In der Abbildung oben zeigt das rote Rechteck die Koeffizienten (b1 und b2) an. Du kannst diese Koeffizienten auf folgende Weise interpretieren:
Wenn man Kinder mit der gleichen Anzahl von Geschwistern vergleicht, steigt die durchschnittliche vorhergesagte Größe um 0,63 cm für jeden Monat, den das Kind Geschwister hat. Ebenso nimmt die Körpergröße beim Vergleich gleichaltriger Kinder um -0,01 cm ab (weil der Koeffizient negativ ist), wenn die Anzahl der Geschwister steigt.
Um einen weiteren Koeffizienten hinzuzufügen, fügst du in R das Symbol "+" für jede zusätzliche Variable hinzu, die du dem Modell hinzufügen möchtest.
lmHeight2 = lm(height~age + no_siblings, data = ageandheight) #Create a linear regression with two variables
summary(lmHeight2) #Review the resultsWie du vielleicht schon gemerkt hast, ist die Anzahl der Geschwister ein alberner Weg, um die Größe eines Kindes vorherzusagen. Ein weiterer Aspekt, auf den du bei deinen linearen Modellen achten solltest, ist der p-Wert der Koeffizienten. Im vorherigen Beispiel zeigt das blaue Rechteck die p-Werte für die Koeffizienten Alter und Anzahl der Geschwister an. Vereinfacht ausgedrückt, gibt ein p-Wert an, ob du eine Hypothese ablehnen oder annehmen kannst oder nicht. Die Hypothese ist in diesem Fall, dass der Prädiktor für dein Modell nicht sinnvoll ist.
- Der p-Wert für das Alter beträgt 4,34*e-10 oder 0,000000000434. Ein sehr kleiner Wert bedeutet, dass das Alter wahrscheinlich eine hervorragende Ergänzung für dein Modell ist.
- Der p-Wert für die Anzahl der Geschwister beträgt 0,85. Mit anderen Worten: Es besteht eine 85%ige Chance, dass dieser Prädiktor für die Regression nicht aussagekräftig ist.
Eine Standardmethode, um zu prüfen, ob die Prädiktoren nicht aussagekräftig sind, ist die Prüfung, ob die p-Werte kleiner als 0,05 sind.
Was sind Residuen?
Eine gute Möglichkeit, die Qualität der Anpassung des Modells zu prüfen, ist die Betrachtung der Residuen oder der Differenzen zwischen den realen Werten und den vorhergesagten Werten. Die gerade Linie in der Abbildung oben stellt die vorhergesagten Werte dar. Die rote vertikale Linie zwischen der Geraden und dem beobachteten Datenwert ist der Restwert.
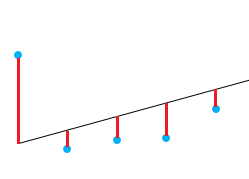
Dabei geht es darum, dass die Summe der Residuen annähernd Null oder so niedrig wie möglich ist. Im wirklichen Leben folgen die meisten Fälle nicht einer perfekt geraden Linie, so dass Residuen zu erwarten sind. In der R-Zusammenfassung der Funktion lm() kannst du deskriptive Statistiken über die Residuen des Modells sehen. Das rote Quadrat zeigt, dass die Residuen annähernd Null sind.
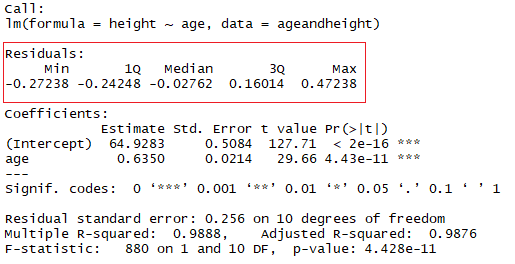
So testest du, ob dein lineares Modell gut passt
Ein Maß, mit dem du testen kannst, wie gut dein Modell ist, ist das Bestimmtheitsmaß (R²). Dieses Maß ist definiert durch den Anteil der Gesamtvariabilität, der durch das Regressionsmodell erklärt wird.
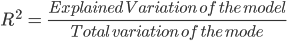
Das kann ein bisschen kompliziert erscheinen, aber im Allgemeinen liegt R² bei Modellen, die gut zu den Daten passen, nahe bei 1. Modelle, die schlecht zu den Daten passen, haben ein R² nahe 0. In den Beispielen unten hat das erste einen R²-Wert von 0,02; das bedeutet, dass das Modell nur 2% der Datenvariabilität erklärt. Die zweite hat ein R² von 0,99, und das Modell kann 99% der gesamten Variabilität erklären.**
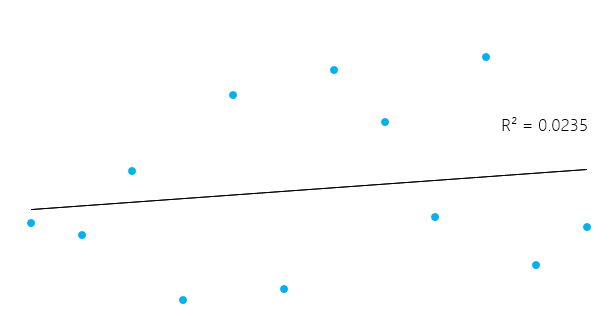
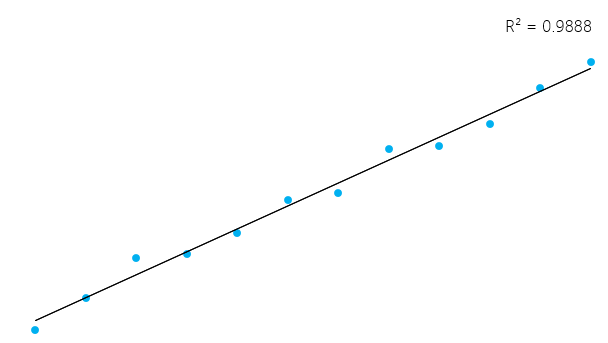
Es ist jedoch wichtig zu bedenken, dass ein hohes R² nicht immer gut ist (siehe unten) und ein niedriges R² nicht immer schlecht ist. Im wirklichen Leben passen die Ereignisse nicht immer in eine perfekte gerade Linie. Du kannst in deinen Daten zum Beispiel größere oder kleinere Kinder im gleichen Alter haben. In manchen Bereichen gilt ein R² von 0,5 als gut.
Sieh dir im gleichen Beispiel wie oben die Zusammenfassung des linearen Modells an, um sein R² zu sehen.
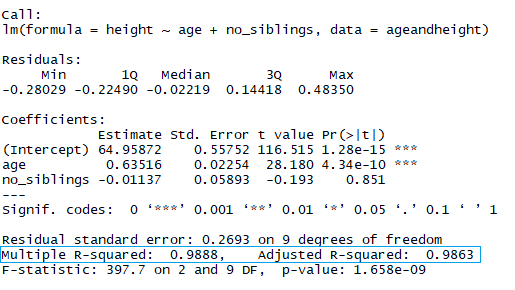
Im blauen Rechteck siehst du, dass es zwei verschiedene R² gibt, ein multiples und ein angepasstes. Der Multiplikator ist das R², das du zuvor gesehen hast. Ein Problem mit diesem R²-Wert ist, dass er nicht sinken kann, wenn du mehr unabhängige Variablen zu deinem Modell hinzufügst. Er steigt weiter an, wenn du das Modell komplexer machst, selbst wenn diese Variablen nichts zu deinen Vorhersagen beitragen (wie im Beispiel der Anzahl der Geschwister). Aus diesem Grund ist das bereinigte R² wahrscheinlich besser geeignet, wenn du mehr als eine Variable zum Modell hinzufügst, da es sich nur erhöht, wenn es den Gesamtfehler der Vorhersagen verringert.
Untersuche die Residuen
Du kannst ein ziemlich gutes R² in deinem Modell haben, aber wir sollten hier keine voreiligen Schlüsse ziehen. Sehen wir uns ein Beispiel an. Du sollst den Druck eines Materials in einem Labor auf der Grundlage seiner Temperatur vorhersagen.
Stellen wir die Daten (in einem einfachen Streudiagramm) dar und fügen die Linie hinzu, die du mit deinem linearen Modell erstellt hast. In diesem Beispiel lässt du R zuerst die Daten einlesen, wiederum mit dem Befehl read_excel, um einen Datenrahmen mit den Daten zu erstellen und dann eine lineare Regression mit deinen neuen Daten zu erstellen. Der Befehl plot() nimmt einen Datenrahmen und stellt die Variablen darin dar. In diesem Fall wird der Druck gegen die Temperatur des Materials aufgetragen. Füge dann die Linie, die durch die lineare Regression entstanden ist, mit dem Befehl abline hinzu.
pressure <- read_excel("pressure.xlsx") #Upload the data
lmTemp = lm(Pressure~Temperature, data = pressure) #Create the linear regression
plot(pressure, pch = 16, col = "blue") #Plot the results
abline(lmTemp) #Add a regression line
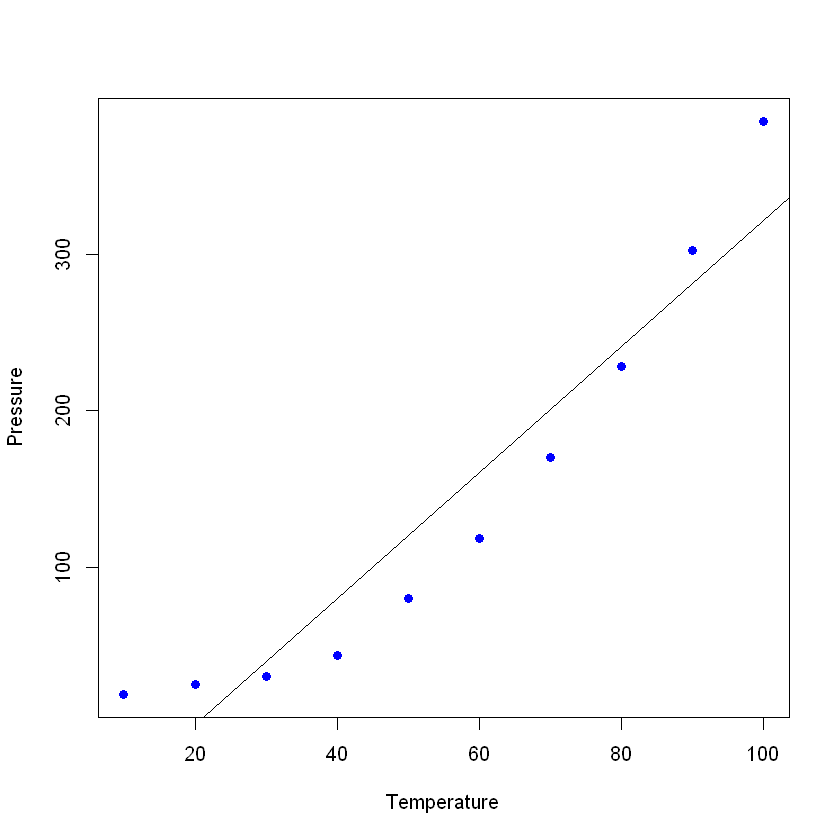
Wenn du dir die Zusammenfassung deines neuen Modells ansiehst, kannst du sehen, dass es ziemlich gute Ergebnisse liefert (sieh dir das R² und das bereinigte R² an)
summary(lmTemp)
Call:
lm(formula = Pressure ~ Temperature, data = pressure)
Residuals:
Min 1Q Median 3Q Max
-41.85 -34.72 -10.90 24.69 63.51
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -81.5000 29.1395 -2.797 0.0233 *
Temperature 4.0309 0.4696 8.583 2.62e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 42.66 on 8 degrees of freedom
Multiple R-squared: 0.902, Adjusted R-squared: 0.8898
F-statistic: 73.67 on 1 and 8 DF, p-value: 2.622e-05Wenn du die Residuen aufzeichnest, sollten sie im Idealfall zufällig aussehen. Andernfalls bedeutet das, dass es vielleicht ein verstecktes Muster gibt, das das lineare Modell nicht berücksichtigt. Um die Residuen darzustellen, verwendest du den Befehl plot(lmTemp$residuals).
plot(lmTemp$residuals, pch = 16, col = "red")
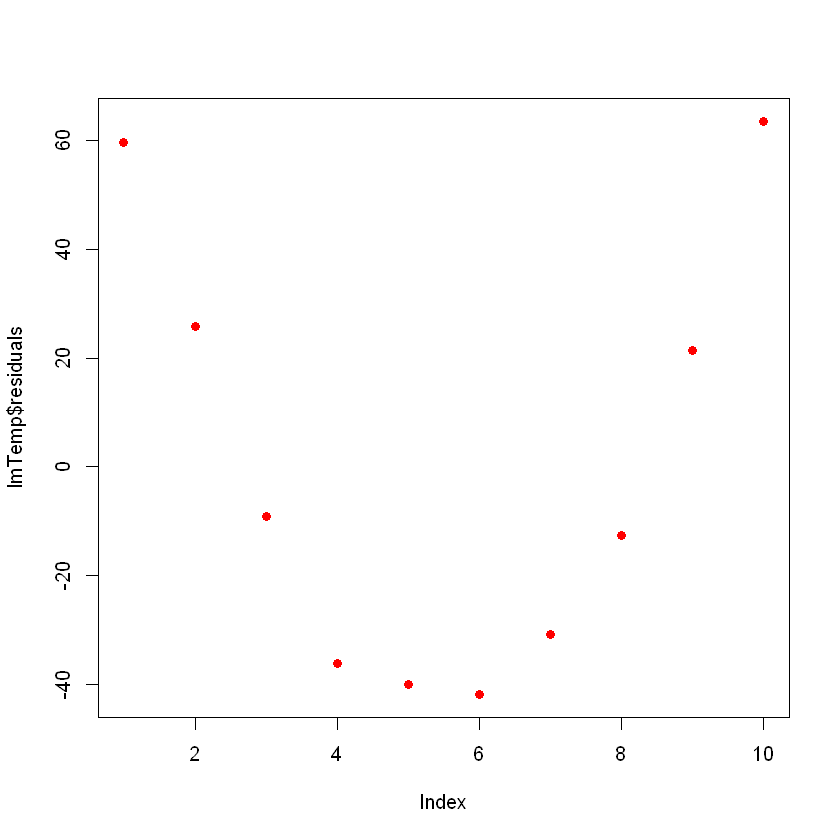
Das kann ein Problem sein. Wenn du mehr Daten hast, kann dein einfaches lineares Modell nicht mehr gut verallgemeinert werden. In der vorherigen Abbildung siehst du, dass es ein Muster gibt (wie eine Kurve auf den Residuen). Das ist ganz und gar nicht zufällig.
Was du tun kannst, ist eine Transformation der Variablen. Es gibt viele Möglichkeiten, deine Daten zu transformieren, z. B. durch Hinzufügen eines quadratischen Terms (x 2), eines kubischen Terms (x3) oder noch komplexere wie ln(X), ln(X+1), sqrt(X), 1/x, Exp(X). Um die richtige Transformation zu finden, brauchst du einige Kenntnisse über algebraische Funktionen, Übung, Versuch und Irrtum.
Versuchen wir es mit einem quadratischen Term. Füge dazu den Begriff "I" (Großbuchstabe "I") vor deiner Transformation hinzu, zum Beispiel die normale lineare Regressionsformel:
lmTemp2 = lm(Pressure~Temperature + I(Temperature^2), data = pressure) #Create a linear regression with a quadratic coefficient
summary(lmTemp2) #Review the results
Call:
lm(formula = Pressure ~ Temperature + I(Temperature^2), data = pressure)
Residuals:
Min 1Q Median 3Q Max
-4.6045 -1.6330 0.5545 1.1795 4.8273
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 33.750000 3.615591 9.335 3.36e-05 ***
Temperature -1.731591 0.151002 -11.467 8.62e-06 ***
I(Temperature^2) 0.052386 0.001338 39.158 1.84e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.074 on 7 degrees of freedom
Multiple R-squared: 0.9996, Adjusted R-squared: 0.9994
F-statistic: 7859 on 2 and 7 DF, p-value: 1.861e-12Beachte, dass sich das Modell deutlich verbessert hat. Wenn du die Residuen des neuen Modells aufzeichnest, sehen sie wie folgt aus:
plot(lmTemp2$residuals, pch = 16, col = "red")
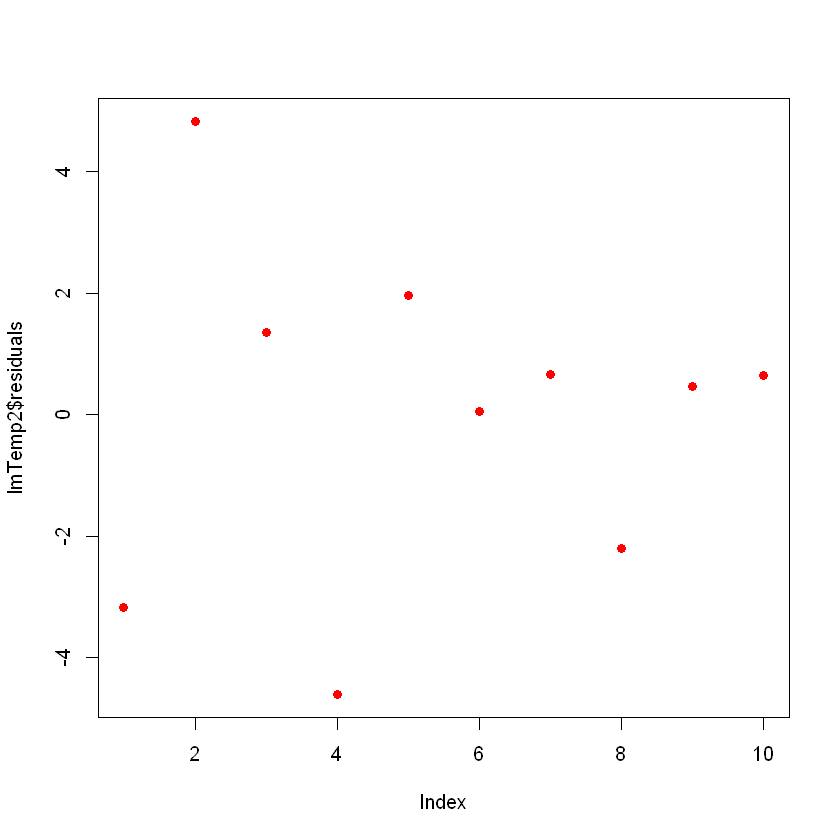
Jetzt siehst du keine klaren Muster mehr in deinen Residuen, und das ist gut so!
Einflussreiche Punkte erkennen
In deinen Daten gibt es möglicherweise einflussreiche Punkte, die dein Modell unnötig verzerren können. Stell dir vor, du hast einen Fehler bei der Dateneingabe gemacht und statt "2,3" wurde der Wert "23" geschrieben. Die häufigste Art von Einflusspunkten sind die Ausreißer, also Datenpunkte, bei denen die beobachtete Reaktion nicht dem Muster zu folgen scheint, das durch den Rest der Daten festgelegt wurde.
Du kannst einflussreiche Punkte erkennen, indem du das Objekt, das das lineare Modell enthält, mit der Funktion cooks.distance() betrachtest und dann diese Abstände aufzeichnest. Ändere absichtlich einen Wert, um zu sehen, wie er auf dem Cooks Distance Plot aussieht. Um einen bestimmten Wert zu ändern, kannst du mit ageandheight[row number, column number] = [new value] direkt auf ihn zeigen. In diesem Fall wird die Höhe auf 7,7 des zweiten Beispiels geändert:
ageandheight[2, 2] = 7.7
head(ageandheight)
| Alter | height | no_siblings |
|---|---|---|
| 18 | 76.1 | 0 |
| 19 | 7.7 | 2 |
| 20 | 78.1 | 0 |
| 21 | 78.2 | 3 |
| 22 | 78.8 | 4 |
| 23 | 79.7 | 1 |
Du erstellst das Modell erneut und siehst, wie schlecht die Zusammenfassung passt, und stellst dann die Cooks-Distanzen dar. Verwende dazu nach der Erstellung der linearen Regression den Befehl cooks.distance([linear model] und dann, wenn du willst, kannst du diese Abstände mit dem Befehl plot() darstellen.
lmHeight3 = lm(height~age, data = ageandheight)#Create the linear regression
summary(lmHeight3)#Review the results
plot(cooks.distance(lmHeight3), pch = 16, col = "blue") #Plot the Cooks Distances.
Call:
lm(formula = height ~ age, data = ageandheight)
Residuals:
Min 1Q Median 3Q Max
-53.704 -2.584 3.609 9.503 17.512
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.905 38.319 0.206 0.841
age 2.816 1.613 1.745 0.112
Residual standard error: 19.29 on 10 degrees of freedom
Multiple R-squared: 0.2335, Adjusted R-squared: 0.1568
F-statistic: 3.046 on 1 and 10 DF, p-value: 0.1115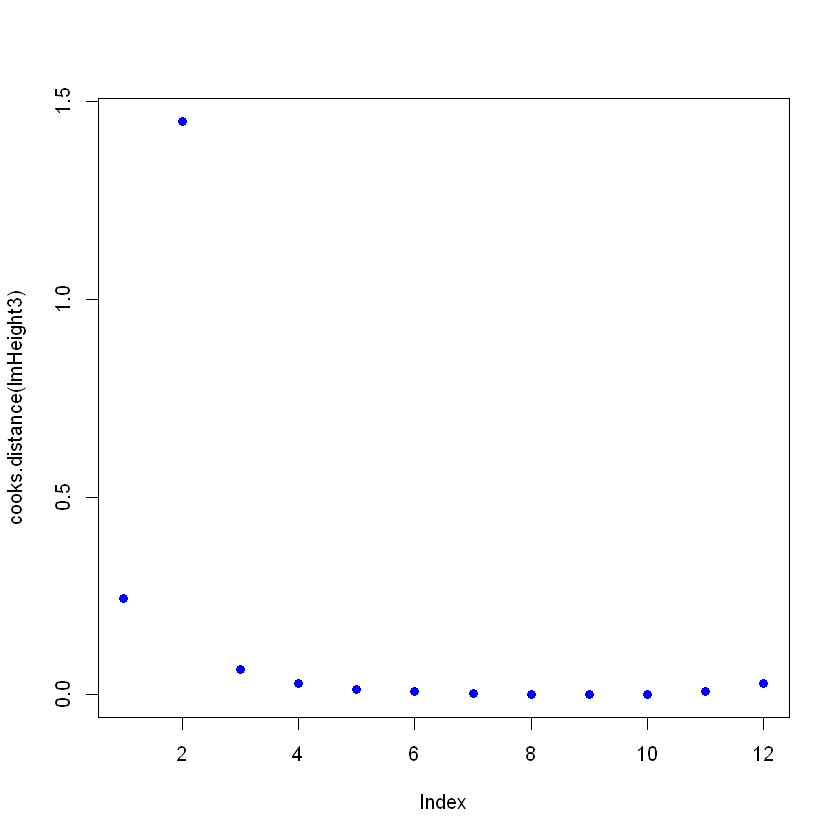
Beachte, dass es einen Punkt gibt, der nicht dem Muster folgt und das Modell beeinträchtigen könnte. Hier kannst du Entscheidungen zu diesem Punkt treffen. Im Allgemeinen gibt es drei Gründe, warum ein Punkt so einflussreich ist:
- Jemand hat einen Aufnahmefehler gemacht
- Jemand hat einen grundlegenden Fehler beim Sammeln der Beobachtung gemacht
- Der Datenpunkt ist absolut gültig, in diesem Fall kann das Modell das Verhalten nicht erklären.
Wenn der Fall 1 oder 2 ist, dann kannst du den Punkt entfernen (oder korrigieren). Wenn es 3 ist, lohnt es sich nicht, einen gültigen Punkt zu streichen; vielleicht kannst du es mit einem nicht-linearen Modell statt mit einem linearen Modell wie der linearen Regression versuchen.
Achte darauf, dass ein einflussreicher Punkt ein gültiger Punkt sein kann, überprüfe die Daten und ihre Quelle, bevor du sie löschst. Dieses Zitat findet man häufig in Statistikbüchern: "Manchmal verwerfen wir gute Daten, wenn wir fragwürdige Modelle verwerfen sollten."
Fazit
Du hast es bis zum Ende geschafft! Die lineare Regression ist ein großes Thema, und sie wird es auch bleiben. Hier stellen wir dir ein paar Tricks vor, mit denen du einen so mächtigen und doch einfachen Algorithmus optimieren kannst. Du hast auch gelernt, was hinter diesem einfachen statistischen Modell steckt und wie du es an deine Bedürfnisse anpassen kannst. Du kannst auch andere Optionen erkunden, indem du ?lm auf der R-Konsole eingibst und dir die verschiedenen Parameter ansiehst, die hier nicht behandelt werden. Schau dir unser Regularization Tutorial an: Ridge, Lasso und Elastic Net. Wenn du dich für statistische Modelle interessierst, solltest du dir den Kurs Statistical Modeling in R ansehen.
Verbessere die Datenkenntnisse deines Teams durch kontinuierliches Lernen
Da die lineare Regression die Grundlage für viele fortschrittliche Analysetechniken bildet, ist es für den langfristigen Erfolg entscheidend, dass dein Team diese und andere wichtige Fähigkeiten beherrscht.
Das DataCamp for Business ist eine maßgeschneiderte Lösung für Unternehmen, die ihre Teams in Data Science und Analytics weiterbilden wollen. Mit benutzerdefinierten Lernpfaden und praktischen Kursen, die ein breites Spektrum an statistischen Methoden, einschließlich Regression und prädiktiver Modellierung, abdecken, kann dein Team selbstbewusst mit komplexen Datenherausforderungen umgehen.
Fordere noch heute eine Demo an und investiere in die Zukunft deines Unternehmens, indem du dein Team in die Lage versetzst, mit den neuesten Tools und Techniken der Datenanalyse auf dem Laufenden zu bleiben.
Lass dich für deine Traumrolle als Data Scientist zertifizieren
Unsere Zertifizierungsprogramme helfen dir, dich von anderen abzuheben und potenziellen Arbeitgebern zu beweisen, dass deine Fähigkeiten für den Job geeignet sind.
Häufig gestellte Fragen
Was ist R^2 bei der linearen Regression?
R^2, das Bestimmtheitsmaß, misst den Anteil der Varianz in der abhängigen Variable, der durch die unabhängige(n) Variable(n) vorhersagbar ist. Er reicht von 0 bis 1, wobei höhere Werte eine bessere Anpassung anzeigen.
Wie lautet die Formel für das R-Quadrat?
Das R-Quadrat wird als der Anteil der Gesamtvariabilität der abhängigen Variable berechnet, der durch das Regressionsmodell erklärt wird. Sie vergleicht die Summe der quadrierten Unterschiede zwischen den beobachteten und den vorhergesagten Werten mit der Gesamtsumme der quadrierten Unterschiede zum Mittelwert der beobachteten Werte.
Was ist die Bedeutung von R in der linearen Regression?
Bei der linearen Regression stellt R den Korrelationskoeffizienten zwischen den beobachteten und vorhergesagten Werten der abhängigen Variable dar. Sie gibt die Stärke und Richtung der linearen Beziehung an.