Curso
O que é uma regressão linear?
Uma regressão linear é um modelo estatístico que analisa a relação entre uma variável de resposta (geralmente chamada de y) e uma ou mais variáveis e suas interações (geralmente chamadas de x ou variáveis explicativas). Por exemplo, quando você calcula a idade de uma criança com base na altura dela, você supõe que quanto mais velha ela for, mais alta ela será.
A regressão linear é um dos modelos estatísticos mais básicos que existem, seus resultados podem ser interpretados por quase todo mundo e ela existe desde o século XIX. É exatamente isso que torna a regressão linear tão popular. É simples e tem sobrevivido por centenas de anos. Embora não seja tão sofisticado quanto outros algoritmos, como redes neurais artific iais ou florestas aleatórias, de acordo com uma pesquisa feita pela KD Nuggets, a regressão foi o algoritmo mais usado pelos cientistas de dados em 2016 e 2017. Até mesmo a previsão é de que ele ainda será usado no ano de 2118!
Neste tutorial de regressão linear, exploraremos como criar uma regressão linear no R, analisando as etapas necessárias com um exemplo que você pode usar.
Para executar facilmente todos os exemplos de código deste tutorial, você pode criar gratuitamente uma pasta de trabalho do DataLab que tenha o R pré-instalado e contenha todos os exemplos de código. Para praticar mais a regressão linear, confira este exercício prático do DataCamp.
Criando uma regressão linear no R
Nem todos os problemas podem ser resolvidos com o mesmo algoritmo. Nesse caso, a regressão linear pressupõe que existe uma relação linear entre a variável de resposta e as variáveis explicativas. Isso significa que você pode ajustar uma linha entre as duas (ou mais variáveis). No exemplo anterior da idade da criança, fica claro que há uma relação entre a idade das crianças e sua altura.
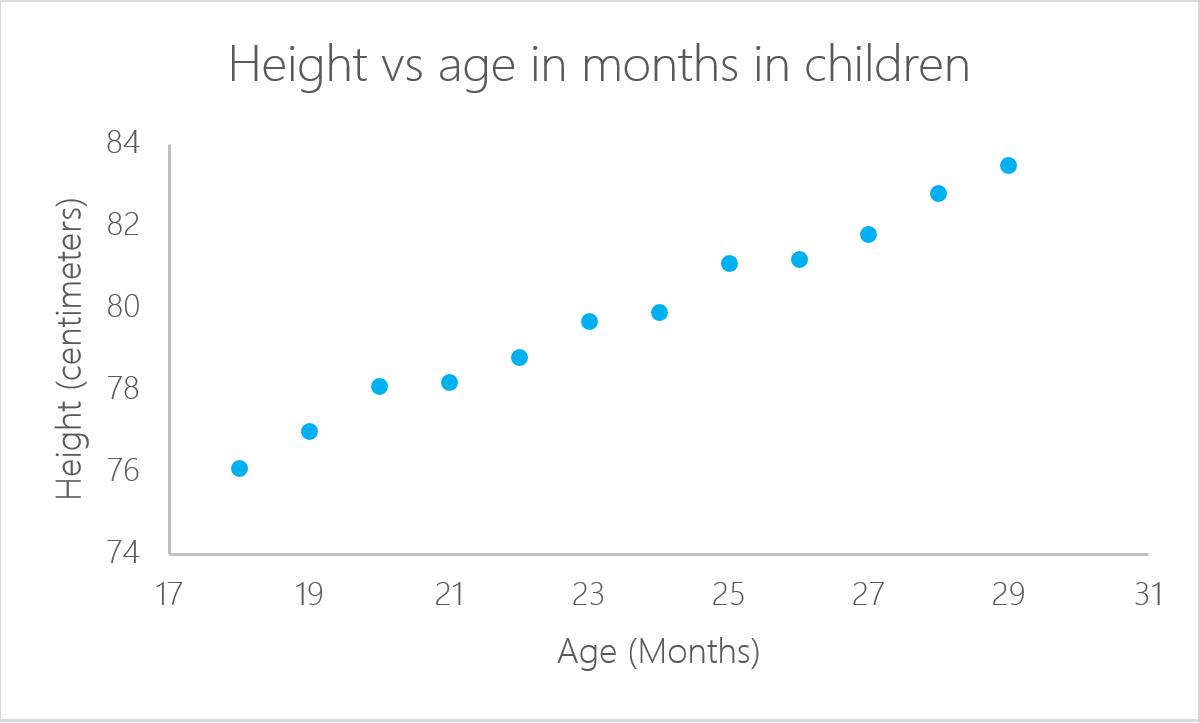
Neste exemplo específico, você pode calcular a altura de uma criança se souber a idade dela:
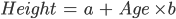
Nesse caso, "a" e "b" são chamados de interceptação e inclinação, respectivamente. Com o mesmo exemplo, "a", ou a interceptação, é o valor a partir do qual você começa a medir. Bebês recém-nascidos com zero meses não têm necessariamente zero centímetros; essa é a função do intercepto. A inclinação mede a mudança na altura com relação à idade em meses. Em geral, para cada mês de idade da criança, sua altura aumentará com "b".
lm em R
Uma regressão linear pode ser calculada no R com o comando lm. No próximo exemplo, use esse comando para calcular a altura com base na idade da criança.
Primeiro, importe a biblioteca readxl para ler arquivos do Microsoft Excel, que podem ser de qualquer tipo de formato, desde que o R possa lê-los. Para saber mais sobre a importação de dados para o R, você pode fazer este curso do DataCamp.
Você pode fazer o download dos dados a serem usados neste tutorial antes de começar. Faça o download dos dados em um objeto chamado ageandheight e, em seguida, crie a regressão linear na terceira linha.
função lm no R:
O comando lm usa as variáveis no formato:
lm([target] ~ [predictor / features], data = [data source])
Com o comando summary(lmHeight), você pode ver informações detalhadas sobre o desempenho e os coeficientes do modelo.
library(readxl)
ageandheight <- read_excel("ageandheight.xls", sheet = "Hoja2") #Upload the data
lmHeight = lm(height~age, data = ageandheight) #Create the linear regression
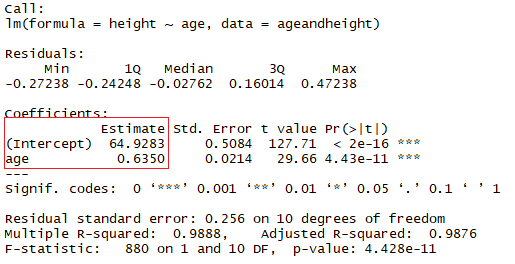
summary(lmHeight) #Review the resultsCoeficientes
No quadrado vermelho, você pode ver os valores da interceptação (valor "a") e da inclinação (valor "b") para a idade. Esses valores "a" e "b" traçam uma linha entre todos os pontos dos dados. Portanto, nesse caso, se houver uma criança com 20,5 meses de idade, a for 64,92 e b for 0,635, o modelo prevê (em média) que sua altura em centímetros será de aproximadamente 64,92 + (0,635 * 20,5) = 77,93 cm.
Quando uma regressão leva em conta dois ou mais preditores para criar a regressão linear, ela é chamada de regressão linear múltipla. Pela mesma lógica que você usou no exemplo simples anterior, a altura da criança será medida por:
Altura = a + Idade × b1 + (Número de irmãos) × b2
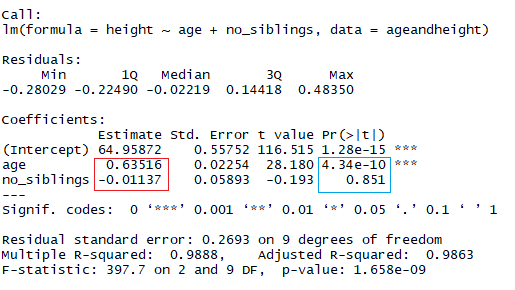
Agora você está analisando a altura como uma função da idade em meses e o número de irmãos que a criança tem. Na imagem acima, o retângulo vermelho indica os coeficientes (b1 e b2). Você pode interpretar esses coeficientes da seguinte maneira:
Ao comparar crianças com o mesmo número de irmãos, a altura média prevista aumenta em 0,63 cm para cada mês que a criança tem. Da mesma forma, ao comparar crianças com a mesma idade, a altura diminui (porque o coeficiente é negativo) em -0,01 cm para cada aumento no número de irmãos.
No R, para adicionar outro coeficiente, adicione o símbolo "+" para cada variável adicional que você deseja adicionar ao modelo.
lmHeight2 = lm(height~age + no_siblings, data = ageandheight) #Create a linear regression with two variables
summary(lmHeight2) #Review the resultsComo você já deve ter percebido, observar o número de irmãos é uma maneira tola de prever a altura de uma criança. Outro aspecto ao qual você deve prestar atenção em seus modelos lineares é o valor p dos coeficientes. No exemplo anterior, o retângulo azul indica os valores de p para os coeficientes de idade e número de irmãos. Em termos simples, um valor p indica se você pode ou não rejeitar ou aceitar uma hipótese. A hipótese, nesse caso, é que o preditor não é significativo para o seu modelo.
- O valor de p para idade é 4,34*e-10 ou 0,000000000434. Um valor muito pequeno significa que a idade provavelmente é uma excelente adição ao seu modelo.
- O valor de p para o número de irmãos é 0,85. Em outras palavras, há 85% de chance de que esse preditor não seja significativo para a regressão.
Uma maneira padrão de testar se os preditores não são significativos é verificar se os valores de p são menores que 0,05.
Resíduos
Uma boa maneira de testar a qualidade do ajuste do modelo é observar os resíduos ou as diferenças entre os valores reais e os valores previstos. A linha reta na imagem acima representa os valores previstos. A linha vertical vermelha da linha reta até o valor dos dados observados é o resíduo.
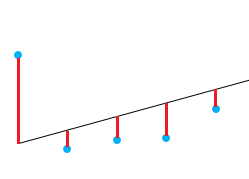
A ideia aqui é que a soma dos resíduos seja aproximadamente zero ou tão baixa quanto possível. Na vida real, a maioria dos casos não seguirá uma linha perfeitamente reta, portanto, os resíduos são esperados. No resumo em R da função lm, você pode ver as estatísticas descritivas sobre os resíduos do modelo, seguindo o mesmo exemplo, o quadrado vermelho mostra como os resíduos são aproximadamente zero.
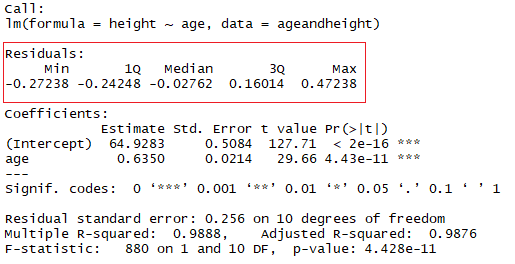
Como testar se o seu modelo linear tem um bom ajuste
Uma medida muito usada para testar a qualidade do seu modelo é o coeficiente de determinação ou R². Essa medida é definida pela proporção da variabilidade total explicada pelo modelo de regressão.
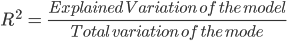
Isso pode parecer um pouco complicado, mas, em geral, para modelos que se ajustam bem aos dados, o R² é próximo de 1. Os modelos que se ajustam mal aos dados têm R² próximo de 0. Nos exemplos abaixo, o primeiro tem um R² de 0,02, o que significa que o modelo explica apenas 2% da variabilidade dos dados. O segundo tem um R² de 0,99, e o modelo pode explicar 99% da variabilidade total.**
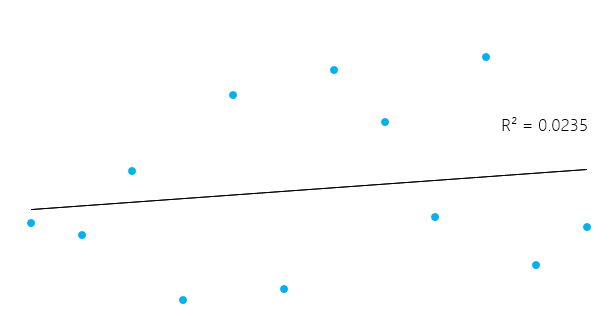
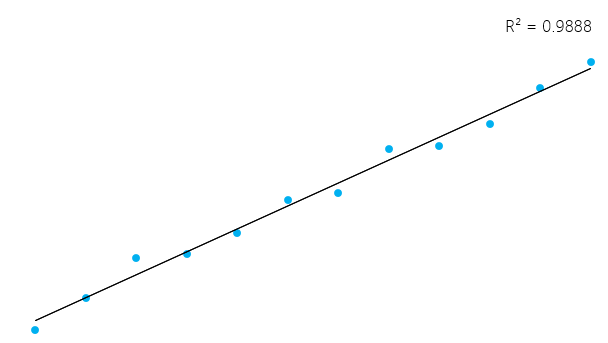
No entanto, é essencial ter em mente que, às vezes, um R² alto não é necessariamente bom todas as vezes (veja os gráficos residuais abaixo) e um R² baixo não é necessariamente sempre ruim. Na vida real, os eventos não se encaixam em uma linha perfeitamente reta o tempo todo. Por exemplo, você pode ter em seus dados crianças mais altas ou mais baixas com a mesma idade. Em alguns campos, um R² de 0,5 é considerado bom.
Com o mesmo exemplo acima, observe o resumo do modelo linear para ver seu R².
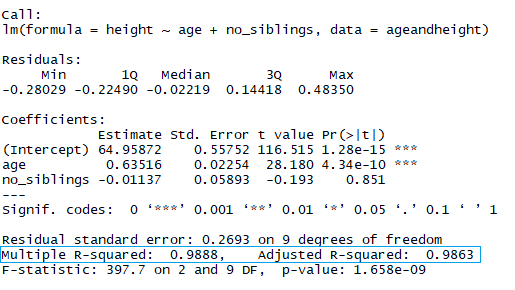
No retângulo azul, observe que há dois R² diferentes, um múltiplo e um ajustado. O múltiplo é o R² que você viu anteriormente. Um problema com esse R² é que ele não pode diminuir à medida que você adiciona mais variáveis independentes ao seu modelo; ele continuará aumentando à medida que você torna o modelo mais complexo, mesmo que essas variáveis não acrescentem nada às suas previsões (como no exemplo do número de irmãos). Por esse motivo, o R² ajustado provavelmente será melhor se você estiver adicionando mais de uma variável ao modelo, pois ele só aumenta se reduzir o erro geral das previsões.
Não se esqueça de analisar os resíduos!
Você pode ter um R² muito bom em seu modelo, mas não vamos tirar conclusões precipitadas. Vamos ver um exemplo. Você vai prever a pressão de um material em um laboratório com base em sua temperatura.
Vamos plotar os dados (em um gráfico de dispersão simples) e adicionar a linha que você construiu com seu modelo linear. Neste exemplo, deixe o R ler os dados primeiro, novamente com o comando read_excel, para criar um dataframe com os dados e, em seguida, criar uma regressão linear com os novos dados. O comando plot obtém um quadro de dados e plota as variáveis nele. Nesse caso, ele plota a pressão em relação à temperatura do material. Em seguida, adicione a linha criada pela regressão linear com o comando abline.
pressure <- read_excel("pressure.xlsx") #Upload the data
lmTemp = lm(Pressure~Temperature, data = pressure) #Create the linear regression
plot(pressure, pch = 16, col = "blue") #Plot the results
abline(lmTemp) #Add a regression line
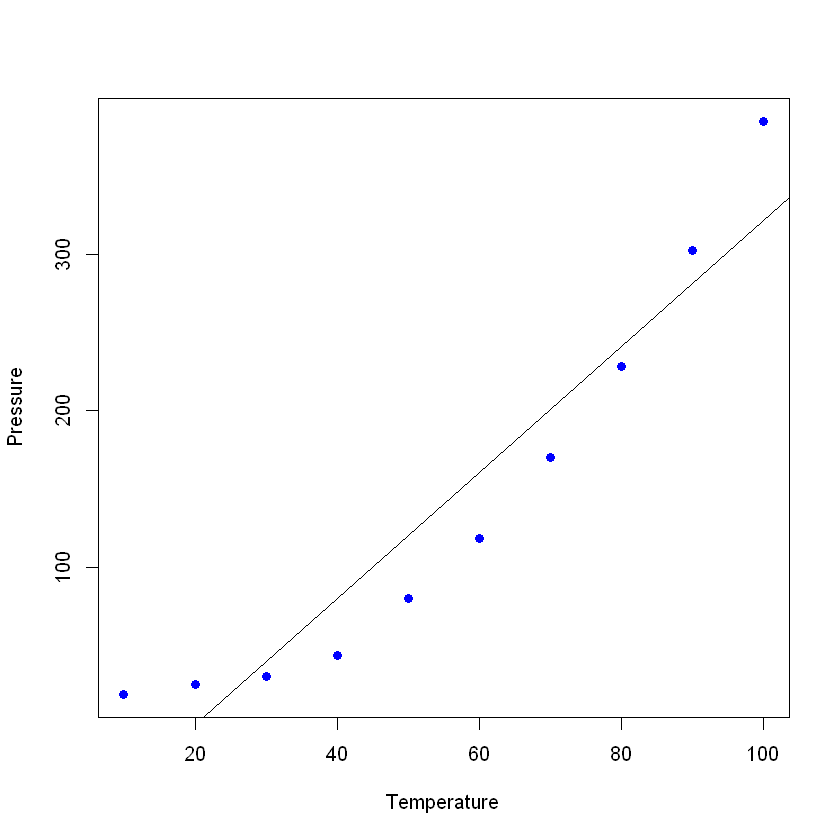
Se você visualizar o resumo do seu novo modelo, verá que ele tem resultados muito bons (observe o R² e o R² ajustado)
summary(lmTemp)
Call:
lm(formula = Pressure ~ Temperature, data = pressure)
Residuals:
Min 1Q Median 3Q Max
-41.85 -34.72 -10.90 24.69 63.51
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -81.5000 29.1395 -2.797 0.0233 *
Temperature 4.0309 0.4696 8.583 2.62e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 42.66 on 8 degrees of freedom
Multiple R-squared: 0.902, Adjusted R-squared: 0.8898
F-statistic: 73.67 on 1 and 8 DF, p-value: 2.622e-05Idealmente, quando você traçar os resíduos, eles devem parecer aleatórios. Caso contrário, isso significa que talvez haja um padrão oculto que o modelo linear não esteja considerando. Para plotar os resíduos, use o comando plot(lmTemp$residuals).
plot(lmTemp$residuals, pch = 16, col = "red")
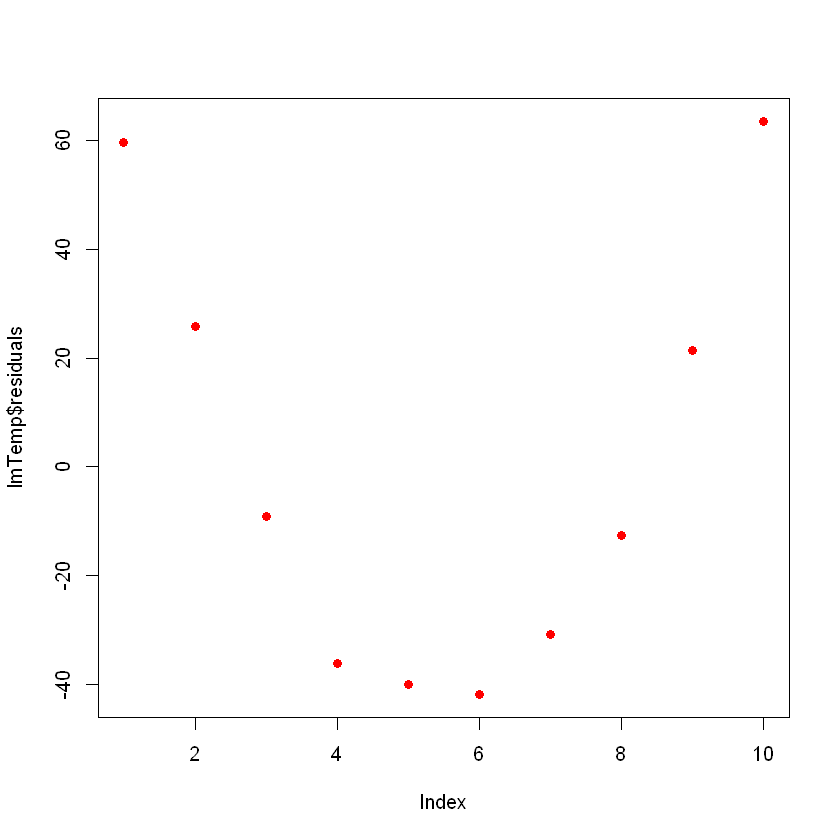
Isso pode ser um problema. Se você tiver mais dados, seu modelo linear simples não conseguirá generalizar bem. Na figura anterior, observe que há um padrão (como uma curva nos resíduos). Isso não é aleatório de forma alguma.
O que você pode fazer é uma transformação da variável. Muitas transformações possíveis podem ser realizadas em seus dados, como a adição de um termo quadrático (x 2), um cúbico (x3) ou ainda mais complexo, como ln(X), ln(X+1), sqrt(X), 1/x, Exp(X). A escolha da transformação correta será feita com algum conhecimento de funções algébricas, prática, tentativa e erro.
Vamos tentar com um termo quadrático. Para isso, adicione o termo "I" ("I" maiúsculo) antes da transformação, por exemplo, essa será a fórmula de regressão linear normal:
lmTemp2 = lm(Pressure~Temperature + I(Temperature^2), data = pressure) #Create a linear regression with a quadratic coefficient
summary(lmTemp2) #Review the results
Call:
lm(formula = Pressure ~ Temperature + I(Temperature^2), data = pressure)
Residuals:
Min 1Q Median 3Q Max
-4.6045 -1.6330 0.5545 1.1795 4.8273
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 33.750000 3.615591 9.335 3.36e-05 ***
Temperature -1.731591 0.151002 -11.467 8.62e-06 ***
I(Temperature^2) 0.052386 0.001338 39.158 1.84e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.074 on 7 degrees of freedom
Multiple R-squared: 0.9996, Adjusted R-squared: 0.9994
F-statistic: 7859 on 2 and 7 DF, p-value: 1.861e-12Observe que o modelo melhorou significativamente. Se você traçar os resíduos do novo modelo, eles terão a seguinte aparência:
plot(lmTemp2$residuals, pch = 16, col = "red")
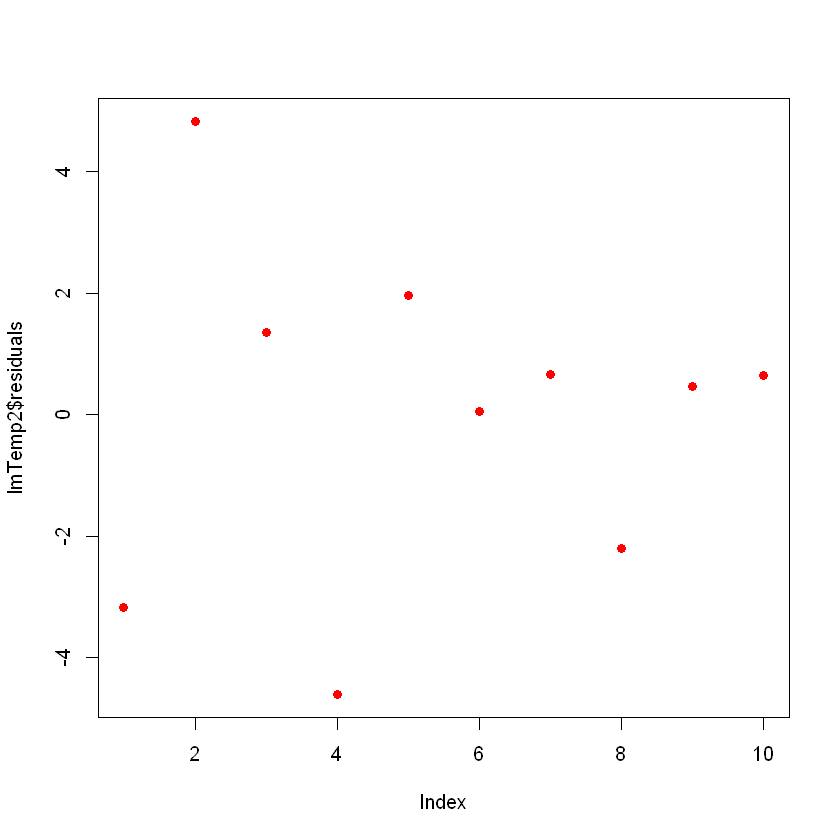
Agora você não vê nenhum padrão claro em seus resíduos, o que é bom!
Detectar pontos influentes
Em seus dados, você pode ter pontos influentes que podem distorcer seu modelo, às vezes desnecessariamente. Pense em um erro na entrada de dados e, em vez de escrever "2,3", o valor era "23". O tipo mais comum de ponto influente são os outliers, que são pontos de dados em que a resposta observada não parece seguir o padrão estabelecido pelo restante dos dados.
Você pode detectar pontos influentes observando o objeto que contém o modelo linear, usando a função cooks.distance e, em seguida, traçar essas distâncias. Altere um valor propositalmente para ver como ele fica no gráfico de distância de Cooks. Para alterar um valor específico, você pode apontar diretamente para ele com ageandheight[row number, column number] = [new value]. Nesse caso, a altura é alterada para 7,7 do segundo exemplo:
ageandheight[2, 2] = 7.7
head(ageandheight)
| idade | altura | no_siblings |
|---|---|---|
| 18 | 76.1 | 0 |
| 19 | 7.7 | 2 |
| 20 | 78.1 | 0 |
| 21 | 78.2 | 3 |
| 22 | 78.8 | 4 |
| 23 | 79.7 | 1 |
Você cria o modelo novamente e vê como o resumo está dando um ajuste ruim e, em seguida, traça as distâncias de Cooks. Para isso, depois de criar a regressão linear, use o comando cooks.distance([linear model] e, em seguida, se quiser, você pode plotar essas distâncias com o comando plot.
lmHeight3 = lm(height~age, data = ageandheight)#Create the linear regression
summary(lmHeight3)#Review the results
plot(cooks.distance(lmHeight3), pch = 16, col = "blue") #Plot the Cooks Distances.
Call:
lm(formula = height ~ age, data = ageandheight)
Residuals:
Min 1Q Median 3Q Max
-53.704 -2.584 3.609 9.503 17.512
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.905 38.319 0.206 0.841
age 2.816 1.613 1.745 0.112
Residual standard error: 19.29 on 10 degrees of freedom
Multiple R-squared: 0.2335, Adjusted R-squared: 0.1568
F-statistic: 3.046 on 1 and 10 DF, p-value: 0.1115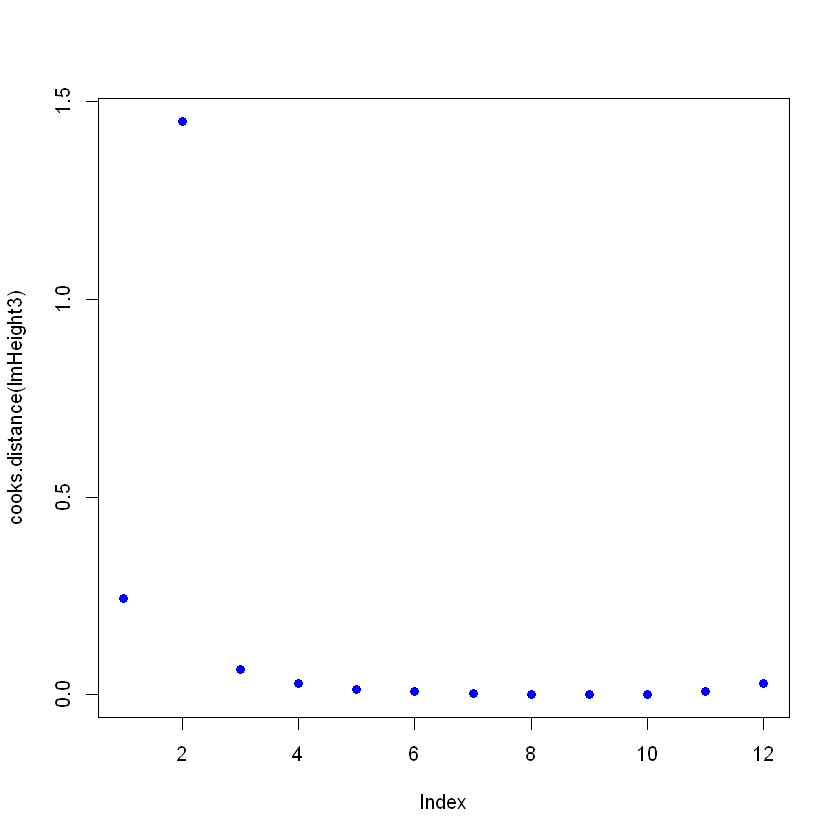
Observe que há um ponto que não segue o padrão, e isso pode estar afetando o modelo. Aqui você pode tomar decisões sobre esse ponto, em geral, há três motivos pelos quais um ponto é tão influente:
- Alguém cometeu um erro de gravação
- Alguém cometeu um erro fundamental ao coletar a observação
- O ponto de dados é perfeitamente válido e, nesse caso, o modelo não pode explicar o comportamento.
Se o caso for 1 ou 2, você poderá remover o ponto (ou corrigi-lo). Se for 3, não vale a pena excluir um ponto válido; talvez você possa tentar usar um modelo não linear em vez de um modelo linear, como a regressão linear.
Esteja ciente de que um ponto influente pode ser um ponto válido; certifique-se de verificar os dados e sua fonte antes de excluí-los. É comum você ver essa citação em livros de estatística: "Às vezes, jogamos fora dados perfeitamente bons quando deveríamos estar jogando fora modelos questionáveis."
Conclusão
Você chegou até o fim! A regressão linear é um tópico importante e veio para ficar. Aqui, apresentamos alguns truques que podem ajudar você a ajustar e tirar o máximo proveito desse algoritmo tão poderoso, porém simples. Você também aprendeu a entender o que está por trás desse modelo estatístico simples e como pode modificá-lo de acordo com suas necessidades. Você também pode explorar outras opções digitando ?lm no console do R e observando os diferentes parâmetros não abordados aqui. Confira nosso tutorial de regularização : Ridge, Lasso e Elastic Net. Se você estiver interessado em se aprofundar em modelos estatísticos, vá em frente e confira o curso sobre Modelagem estatística em R.