PMT() Excel: Berechnung der Darlehenszahlungen und Sparbeiträge

Die Funktion PMT() in Excel berechnet die periodische Zahlung, die erforderlich ist, um ein Darlehen oder eine Investition mit konstanten Zahlungen und einem festen Zinssatz zu begleichen. Er wird häufig bei Finanzmodellen, Haushaltsplanungen und Kreditberechnungen verwendet, um zu ermitteln, wie viel du in jeder Periode für einen Kredit zahlen oder wie viel du zum Erreichen eines Sparziels beitragen musst.

Wenn du zum Beispiel planst, ein Haus zu kaufen und deine monatlichen Hypothekenzahlungen verstehen musst, gibt dir die Funktion PMT() ein klares Bild von deiner finanziellen Verpflichtung. Ebenso nutzen Unternehmen diese Funktion, um die Finanzierung von Ausrüstungen zu planen oder die Zahlungsstrukturen für Ratenzahlungspläne ihrer Kunden festzulegen.

Diese einfache Formel berücksichtigt die Kredithöhe, den Zinssatz und die Laufzeit, um präzise Zahlungsberechnungen zu erstellen, die Einzelpersonen und Unternehmen helfen, fundierte finanzielle Entscheidungen zu treffen.

Schnelle Antwort

Die Funktion PMT() in Excel berechnet regelmäßige Zahlungsbeträge für Darlehen oder Anlagen mit konstanten Zahlungen und einem festen Zinssatz. Bei einer typischen 30-jährigen Hypothek über 300.000 $ mit einem jährlichen Zinssatz von 4,5 % würde die monatliche Zahlung etwa 1.520,06 $ betragen. Die Formel würde lauten:

=PMT(4.5%/12, 30*12, 300000)

PMT()-Funktion Syntax und Parameter

Die Syntax der Funktion PMT() lautet:

=PMT(rate, nper, pv, [fv], [type])

Schauen wir uns die einzelnen Parameter an:

• rate: Zinssatz pro Periode. Wenn dein Kredit einen jährlichen Zinssatz von 6 % hat, aber die Zahlungen monatlich erfolgen, würdest du 6 %/12 oder 0,5 % pro Monat verwenden.

• nper: Gesamtzahl der Zahlungszeiträume. Für einen 5-Jahres-Kredit mit monatlichen Zahlungen würdest du 5*12 oder 60 Perioden verwenden.

• pv: Barwert (Darlehensbetrag oder Kapital). Das ist der ursprüngliche Betrag, den du geliehen oder investiert hast.

• fv (optional): Zukünftiger Wert nach der Abschlusszahlung. Fällt auf 0 weg, was bedeutet, dass der Kredit vollständig zurückgezahlt ist.

• type (optional): Zeitpunkt der Zahlung. Verwende 0 für Zahlungen am Ende der Periode (Standard) oder 1 für Zahlungen am Anfang.

Es ist wichtig, die Cashflow-Konvention in Excel zu verstehen: Zahlungen (Geldabflüsse) werden als negative Zahlen ausgedrückt, während Zuflüsse (Geldzuflüsse) positiv sind. Aus diesem Grund erscheinen die Ergebnisse der Funktion PMT() in der Regel als negative Werte - sie stehen für die Zahlungen, die du leistest.

Anpassungen der Zahlungsfrequenz verstehen

Wenn du die Funktion PMT() verwendest, musst du den Zinssatz und die Anzahl der Perioden an den Aufzinsungsrhythmus des Darlehens anpassen. Viele Kredite haben einen jährlichen Zinssatz, aber die Zahlungen erfolgen in der Regel häufiger.

Hier erfährst du, wie du den Jahressatz und die Anzahl der Perioden auf der Grundlage verschiedener Zahlungsfrequenzen anpassen kannst:

• Monatlich: Jahresrate ÷ 12, Anzahl der Jahre × 12
• Vierteljährlich: Jahresrate ÷ 4, Anzahl der Jahre × 4
• Halbjährlich: Jahresrate ÷ 2, Anzahl der Jahre × 2

Wenn du zum Beispiel ein Darlehen mit einer Laufzeit von 5 Jahren, einem jährlichen Zinssatz von 6 % und monatlichen Raten hast, würdest du das verwenden:

• Bewerten: 6%/12 = 0,5% pro Monat
• Anzahl der Perioden: 5×12 = 60 Monate

Diese Tabelle fasst die Anpassungen für ein Darlehen mit einer Laufzeit von 5 Jahren und einem jährlichen Zinssatz von 6 % zusammen:

Wenn du diese Anpassungen vornimmst, wird sichergestellt, dass deine Zahlungsberechnungen die Aufzinsungshäufigkeit deines Kredits oder deiner Investition genau widerspiegeln.

Häufige Verwendungen der Excel-Funktion PMT()

Schauen wir uns die beiden wahrscheinlich häufigsten Verwendungszwecke an. 

PMT()-Funktion für Hypothekendarlehen

Gehen wir ein Beispiel aus der Praxis durch, um die monatlichen Zahlungen für ein Hypothekendarlehen zu berechnen:

• Darlehensbetrag: $400,000
• Zinssatz: 6% jährlich
• Laufzeit des Darlehens: 20 Jahre
• Zahlungsfrequenz: Monatlich

Zuerst müssen wir die Rate und die Zeiträume anpassen:

• Angepasste Rate: 6%/12 = 0,5% pro Monat
• Angepasste Zeiträume: 20×12 = 240 Monate

Die Formel würde lauten:

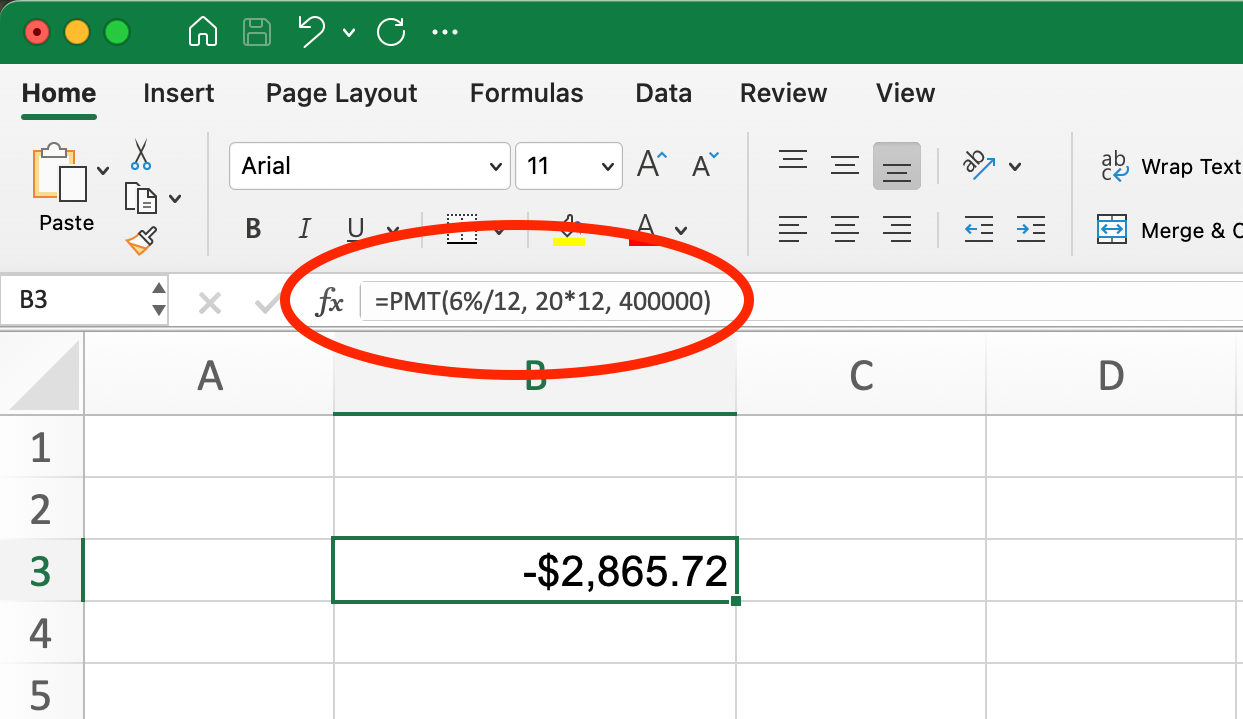
PMT()-Funktion für Hypothekendarlehen. Bild vom Autor.

=PMT(6%/12, 20*12, 400000)

Daraus ergibt sich ein Ergebnis von -$2.865,72. Das negative Vorzeichen zeigt an, dass es sich um eine Zahlung handelt (Abfluss von Barmitteln). Deine monatliche Hypothekenzahlung würde also 2.865,72 $ betragen.

PMT()-Funktion für Ersparnisse und Investitionen

Mit der Funktion PMT() kannst du auch berechnen, wie viel du regelmäßig sparen musst, um ein zukünftiges finanzielles Ziel zu erreichen.

Angenommen, du willst in 18 Jahren 50.000 USD mit einer jährlichen Rendite von 6 % sparen. Wie viel solltest du monatlich einzahlen?

In diesem Fall:

• Zukunftswert (fv): 50.000 $ (dein Ziel)
• Barwert (pv): 0 (vorausgesetzt, du fängst bei Null an)
• Bewerten: 6%/12 = 0,5% monatlich
• Zeiträume: 18×12 = 216 Monate

Die Formel würde lauten:

PMT()-Funktion für Ersparnisse und Investitionen. Bild vom Autor.

=PMT(6%/12, 18*12, 0, 50000)

Das bedeutet, dass du monatlich etwa 129,08 $ einzahlen müsstest, um dein Ziel von 50.000 $ in 18 Jahren zu erreichen, wenn du von einer jährlichen Rendite von 6 % ausgehst.

In diesem Fall verwenden wir einen positiven Wert für den Zukunftswert (50000), weil er Geld darstellt, das du in der Zukunft erhalten wirst. Wenn du berechnest, wie viel du sparen musst, um ein Ziel zu erreichen, ist das Ergebnis von PMT() negativ (was bedeutet, dass du diesen Betrag einzahlen musst) und der zukünftige Wert ist positiv (was bedeutet, dass du am Ende Geld haben wirst).

Häufige Fehler und Fehlersuche

Bei der Arbeit mit der Funktion PMT() kannst du auf Fehlermeldungen oder unerwartete Ergebnisse stoßen. Hier sind einige häufige Probleme und wie du sie lösen kannst:

#NUM! und #VALUE! Fehler

Die Funktion PMT() kann diese Fehler aus verschiedenen Gründen zurückgeben:

• #NUM! erscheint normalerweise, wenn Excel mit den gegebenen Eingaben kein gültiges Ergebnis berechnen kann. Das kann passieren, wenn dein Zinssatz extrem hoch ist oder deine Laufzeit ungewöhnlich lang ist.

• #VALUE! weist normalerweise auf ein Problem mit einem deiner Eingabewerte hin, z. B. auf Text, wo eine Zahl erwartet wird.

Häufige Fehler, die du vermeiden solltest

Vergessen, Rate und Prozentsatz für monatliche/quartalsweise Zahlungen anzupassen

Einer der häufigsten Fehler ist, den jährlichen Zinssatz direkt zu verwenden, anstatt ihn durch die Anzahl der Zahlungen pro Jahr zu teilen. Nimm zum Beispiel 5% statt 5%/12 für die monatlichen Zahlungen.

Incorrect: =PMT(5%, 30*12, 250000)
Correct: =PMT(5%/12, 30*12, 250000)

Eingabe nicht-numerischer Werte

Stelle sicher, dass alle Parameter numerische Werte oder Zellverweise auf numerische Werte enthalten. Wenn du versehentlich Text oder leere Zellen einfügst, führt das zu Fehlern.

Verwendung falscher Vorzeichen (positiv statt negativ)

Denke daran, dass bei Finanzfunktionen Geld, das du ausgibst, negativ und Geld, das du erhältst, positiv sein sollte. Wenn dein Darlehensbetrag (pv) negativ eingegeben wird, erscheint deine Zahlung positiv (und umgekehrt). Für Darlehen:

If PV is positive: PMT will be negative (you're paying out)
If PV is negative: PMT will be positive (appears as money coming in)

Die Periodenzählung verwechseln

Achte darauf, dass deine nper (Anzahl der Perioden) mit deiner Tarifperiode übereinstimmt. Wenn du deine Rate auf eine monatliche Zahl eingestellt hast, sollten auch deine Perioden in Monaten angegeben werden.

Wenn du diese häufigen Fehler behebst, wirst du bei der Verwendung der Funktion PMT() für Finanzberechnungen genaue Ergebnisse erhalten.

Erweiterte Anwendungsfälle und verwandte Funktionen

Die Funktion PMT() lässt sich gut mit anderen Finanzfunktionen in Excel kombinieren, um umfassende Kreditanalysen und Finanzmodelle zu erstellen. Hier erfährst du, wie PMT() mit anderen Finanzfunktionen zusammenarbeitet:

IPMT (Zinsanteil der Zahlung)

Die Funktion IPMT() berechnet den Zinsanteil einer Darlehenszahlung für einen bestimmten Zeitraum. In Kombination mit PMT() kannst du sehen, wie viel von jeder Zahlung in Zinsen fließt.

=IPMT(rate, per, nper, pv, [fv], [type])

Um zu unserem Beispiel mit der 300.000-Dollar-Hypothek zurückzukehren, können wir den Zinsanteil der zwölften Zahlung ermitteln (30-jährige Hypothek mit 4,5 % Jahreszins):

IPMT()-Funktion für Hypothekendarlehen. Bild vom Autor.

=IPMT(4.5%/12, 12, 30*12, 300000)

Das ergibt -$1.108,39, was bedeutet, dass $1.108,39 dieser Zahlung für Zinsen verwendet werden.

PPMT (Hauptanteil der Zahlung)

Die Funktion PPMT() berechnet den Hauptanteil einer Darlehenszahlung für einen bestimmten Zeitraum. Dies zeigt, wie viel von deiner Zahlung den tatsächlichen Kreditsaldo reduziert.

=PPMT(rate, per, nper, pv, [fv], [type])	

Um den Kapitalanteil der 12. Rate zu ermitteln, verwende dasselbe Beispiel für eine Hypothek:

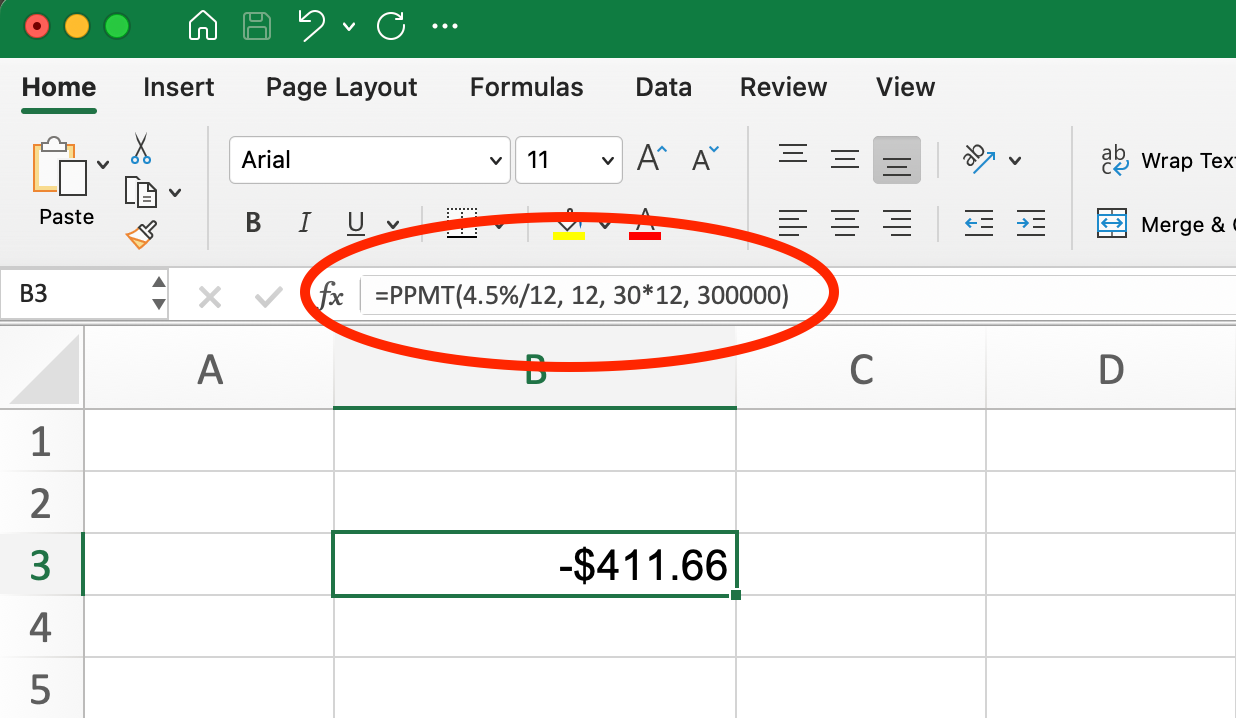
PPMT-Formel für Hypothekendarlehen. Bild vom Autor.

=PPMT(4.5%/12, 12, 30*12, 300000)

Das Ergebnis ist -$411,66, was bedeutet, dass $411,66 zur Verringerung des Kreditsaldos verwendet werden.

Beachte, dass die Summe der Zins- und Tilgungsanteile (-$1.108,39 - $411,66 = -$1.520,05) ungefähr unserem gesamten monatlichen Zahlungsbetrag entspricht. Diese Beziehung ist immer gültig: PMT = IPMT + PPMT für einen bestimmten Zeitraum.

NPER (Anzahl der für ein Darlehen erforderlichen Perioden)

Wenn du weißt, wie viel du dir monatlich leisten kannst, hilft dir NPER() dabei, herauszufinden, wie lange es dauern wird, einen Kredit abzuzahlen:

=NPER(rate, pmt, pv, [fv], [type])

Wenn du zum Beispiel monatlich 2.000 $ für ein Darlehen von 300.000 $ zu 4,5 % Jahreszins zahlen kannst:

NPER-Formel für Hypothekendarlehen. Bild vom Autor.

=NPER(4.5%/12, -2000, 300000)

Das ergibt 220,86, was bedeutet, dass es ungefähr 221 Monate (etwa 18,4 Jahre) dauern würde, um das Darlehen zurückzuzahlen. Das ist deutlich schneller als die Standardlaufzeit von 30 Jahren, weil du mehr als die Mindestrate zahlst.

RATE (Ermittlung des Zinssatzes)

Wenn du den Kreditbetrag, die Ratenhöhe und die Laufzeit kennst, kann RATE() den Zinssatz ermitteln:

=RATE(nper, pmt, pv, [fv], [type], [guess])	

Für ein Darlehen von 300.000 $ mit monatlichen Zahlungen von 1.520,06 $ über 30 Jahre:

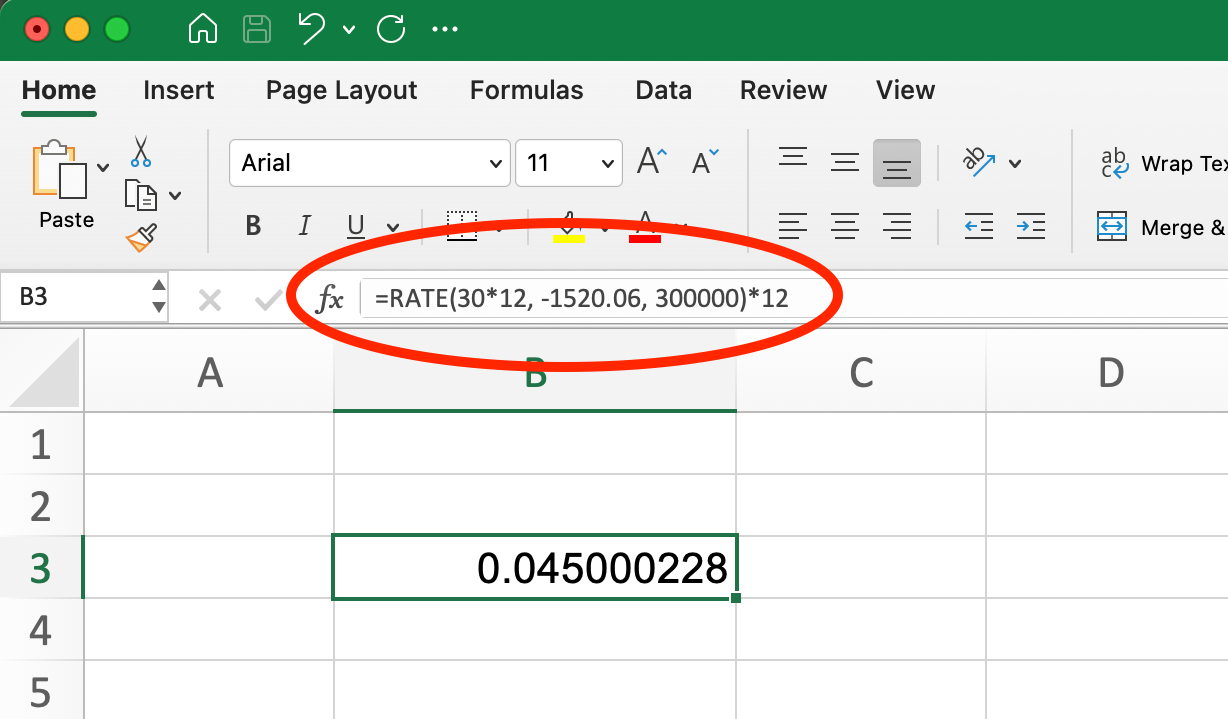
RATENFORMEL für Hypothekendarlehen. Bild vom Autor.

=RATE(30*12, -1520.06, 300000)*12

Das ergibt 4,5 % und bestätigt, dass unsere monatliche Zahlung von 1.520,06 $ einem jährlichen Zinssatz von 4,5 % entspricht. Wir multiplizieren das Ergebnis mit 12, um die monatliche Rate in eine jährliche Rate umzurechnen.

Techniken zur Zielerreichung

Die Funktion "Ziel suchen" von Excel kann dir helfen, Fragen wie diese zu beantworten:

• Wie viel kann ich mir leihen, wenn ich mir eine bestimmte monatliche Rate leisten kann?
• Welchen Zinssatz müsste ich aushandeln, um die Zahlungen unter einem bestimmten Betrag zu halten?

Wenn wir zum Beispiel unsere monatlichen Zahlungen für die 400.000-$-Hypothek aus unserem früheren Beispiel (6 % Zinssatz, 20 Jahre Laufzeit) bei 2.000 $ halten wollen, können wir mit Goal Seek ermitteln, wie viel Anzahlung wir leisten müssen. Eine ausführliche Anleitung zu diesem Thema findest du in unserem Leitfaden zur Verwendung der Zielsuche in Excel.

Diese integrierten Ansätze ermöglichen eine anspruchsvollere Finanzplanung und Entscheidungsfindung, die über einfache Zahlungsberechnungen hinausgeht. Wenn du PMT() mit diesen Funktionen kombinierst, kannst du komplette Tilgungspläne erstellen und verschiedene Finanzszenarien analysieren.

Die wichtigsten Erkenntnisse

Die korrekte Verwendung der Funktion PMT() in Excel erfordert viel Liebe zum Detail, insbesondere bei der Anpassung von Kursen und Zeiträumen. Hier sind die wichtigsten Punkte, die du dir merken solltest:

• Passe deinen Zinssatz und die Anzahl der Perioden immer an die Zahlungsfrequenz an. Für monatliche Zahlungen bei einer jährlichen Rate, teile die Rate durch 12 und multipliziere die Jahre mit 12.

• Die Funktion PMT() folgt einer bestimmten Cashflow-Konvention: Zahlungen, die du leistest, erscheinen als negative Zahlen, während Geld, das du erhältst, als positiv angezeigt wird.

• PMT() arbeitet als Teil einer Familie von Finanzfunktionen (IPMT(), PPMT(), NPER(), RATE()), die zusammen umfassende Kredit- und Investitionsanalysen erstellen können.

• Häufige Fehler können vermieden werden, indem du deine Eingaben doppelt überprüfst, sicherstellst, dass du den Zahlungsrhythmus richtig angepasst hast, und die richtigen Vorzeichen für die Zahlungsströme verwendest.

• Die Funktion PMT() eignet sich nicht nur für Kredite, sondern auch für die Spar- und Investitionsplanung, wenn du regelmäßige Beiträge festlegen musst.

Excel-Vorlagen, die die Funktion PMT() enthalten, können bei der Arbeit mit wiederholten Finanzberechnungen Zeit sparen und Fehler reduzieren. Versuche, eine wiederverwendbare Vorlage für Kreditvergleiche oder Sparpläne zu erstellen, um deine Finanzanalyse zu rationalisieren.

Fazit

Die Anwendung der Funktion PMT() in Excel bietet eine solide Grundlage für fundierte finanzielle Entscheidungen. Ob du Hypothekenzahlungen berechnest, Sparbeiträge planst oder Investitionsmöglichkeiten auswertest, diese vielseitige Funktion hilft dir, die finanziellen Auswirkungen verschiedener Szenarien zu verstehen.

Wenn du die Funktion PMT() mit verwandten Funktionen wie IPMT(), PPMT(), NPER() und RATE() verwendest, kannst du umfassende Finanzmodelle erstellen, die komplexe Fragen zu Darlehen und Investitionen beantworten. Mit Goal Seek und der Szenarioanalyse kannst du verschiedene finanzielle Möglichkeiten ausloten.

Wenn du deine Excel-Kenntnisse vertiefen möchtest, bieten wir dir hervorragende Ressourcen, um deine Lernreise fortzusetzen:

• Unser Lernpfad Excel-Grundlagen ist ideal für alle, die sich ein umfassendes Excel-Grundwissen aneignen wollen, das von der Datenaufbereitung über die Visualisierung bis hin zu Analysetechniken reicht. Dieser Lernpfad erfordert keine Vorkenntnisse und führt dich durch praktische Übungen mit Szenarien aus der Praxis.
• Wenn du dich speziell für Finanzanwendungen interessierst, lernst du in unserem Kurs Finanzmodellierung in Excel, wie du mit Cashflows, Szenarioanalysen, dem Zeitwert des Geldes und der Investitionsrechnung arbeitest. Dieser Kurs auf mittlerem Niveau wird von Fachleuten aus der Branche unterrichtet und beinhaltet praktische Übungen mit Finanzdaten.

Mit diesen Kenntnissen und Ressourcen bist du gut gerüstet, um die Funktion PMT() und verwandte Excel-Tools bei deinen finanziellen Entscheidungsprozessen anzuwenden, um Tilgungspläne für Kredite zu erstellen und anspruchsvolle Investitionsmodelle zu entwickeln.