PMT() Excel: Calculate Loan Payments and Savings Contributions

The PMT() function in Excel calculates the periodic payment required to settle a loan or investment with constant payments and a fixed interest rate. While versatile for various financial calculations, PMT() is most commonly used for determining loan payments, particularly mortgages. It's also used in financial modeling and budgeting to determine how much you'll pay each period for a loan or how much you need to contribute to reaching a savings goal.

If you are doing things like calculating loan payments and interest rates, you may also be interested in learning about cash flow analysis and capital budgeting, in which case you will find our Financial Modeling in Excel course compelling. I recommend it also if you are interested in learning how to deconstruct income statements, and learning the time value of money.

Quick Answer

The PMT() function in Excel calculates regular payment amounts for loans or investments with constant payments and a fixed interest rate. For a typical 30-year $300,000 mortgage with a 4.5% annual interest rate, the monthly payment would be approximately $1,520.06. The formula would be:

=PMT(4.5%/12, 30*12, 300000)

PMT() Function Syntax and Parameters

The syntax of the PMT() function is:

=PMT(rate, nper, pv, [fv], [type])

Let's break down each parameter:

• rate: Interest rate per period. If your loan has an annual interest rate of 6% but payments are made monthly, you'd use 6%/12 or 0.5% per month.

• nper: Total number of payment periods. For a 5-year loan with monthly payments, you'd use 5*12 or 60 periods.

• pv: Present value (loan amount or principal). This is the initial amount borrowed or invested.

• fv (optional): Future value after the final payment. Defaults to 0 if omitted, meaning the loan is fully paid off.

• type (optional): Payment due timing. Use 0 for payments at the end of the period (default) or 1 for payments at the beginning.

It's important to understand the cash flow convention in Excel: Payments (money going out) are expressed as negative numbers, while inflows (money coming in) are positive. This is why PMT() function results typically appear as negative values—they represent payments you're making.

Understanding Payment Frequency Adjustments

When using the PMT() function, you need to adjust the rate and number of periods based on the loan's compounding frequency. Many loans quote annual interest rates, but payments typically occur more frequently.

Here's how to adjust the annual rate and number of periods based on different payment frequencies:

• Monthly: annual rate ÷ 12, number of years × 12
• Quarterly: annual rate ÷ 4, number of years × 4
• Semi-Annually: annual rate ÷ 2, number of years × 2

For example, if you have a 5-year loan with a 6% annual interest rate and monthly payments, you would use:

• Rate: 6%/12 = 0.5% per month
• Number of periods: 5×12 = 60 months

This table summarizes the adjustments for a 5-year loan with a 6% annual interest rate:

Making these adjustments ensures your payment calculations accurately reflect the compounding frequency of your loan or investment.

Common Uses of the Excel PMT() Function

Let's look at what are likely the two most common uses. 

PMT() function for mortgage loans

Let's walk through a real-life example of calculating monthly payments for a mortgage loan:

• Loan amount: $400,000
• Interest rate: 6% annually
• Loan term: 20 years
• Payment frequency: Monthly

First, we need to adjust the rate and periods:

• Adjusted rate: 6%/12 = 0.5% per month
• Adjusted periods: 20×12 = 240 months

The formula would be:

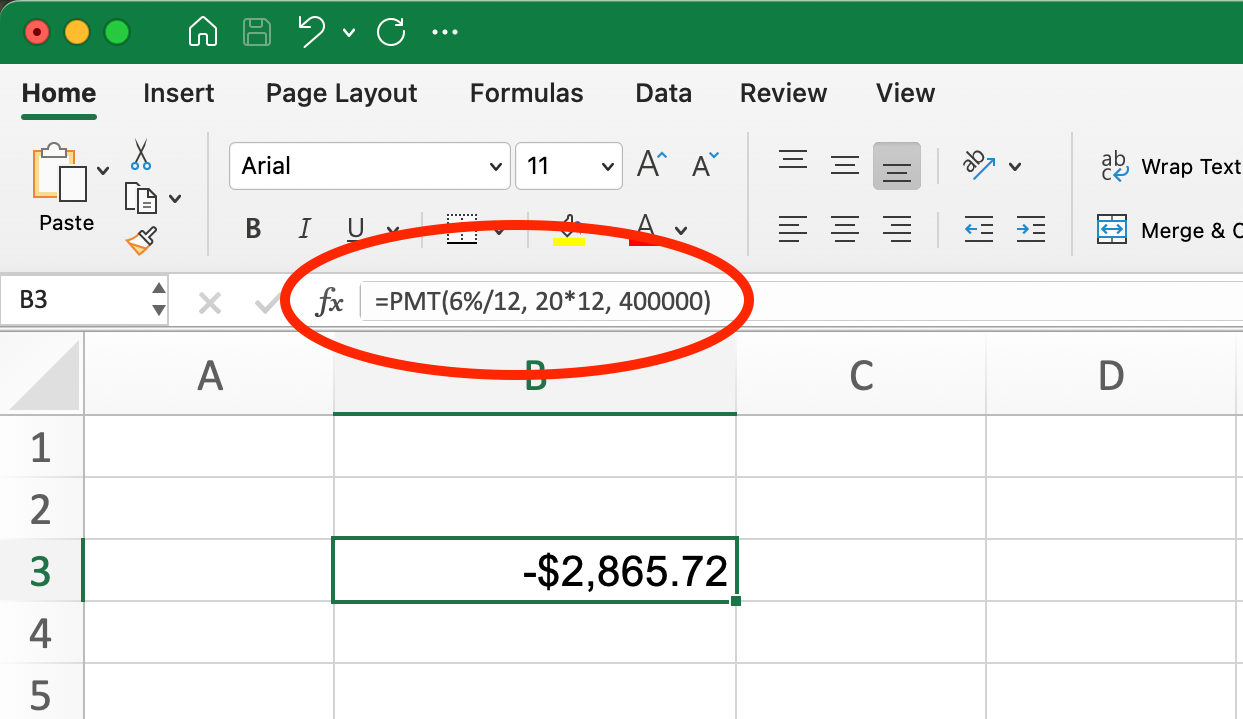
PMT() Function for Mortage Loan. Image by Author.

=PMT(6%/12, 20*12, 400000)

This gives us a result of -$2,865.72. The negative sign indicates this is a payment (outflow of cash). So your monthly mortgage payment would be $2,865.72.

PMT() function for savings and investments

The PMT() function can also help calculate how much you need to save regularly to reach a future financial goal.

For example, suppose you want to save $50,000 in 18 years with a 6% annual return. How much should you contribute monthly?

In this case:

• Future value (fv): $50,000 (your goal)
• Present value (pv): 0 (assuming you're starting from zero)
• Rate: 6%/12 = 0.5% monthly
• Periods: 18×12 = 216 months

The formula would be:

PMT() Function for Savings and Investments. Image by Author.

=PMT(6%/12, 18*12, 0, 50000)

This returns approximately $129.08, meaning you would need to deposit about $130 monthly to reach your $50,000 goal in 18 years, assuming a 6% annual return.

In this case, we use a positive value for the future value (50000) because it represents money you will receive in the future. When calculating how much to save to reach a goal, the PMT() result will be negative (indicating you need to contribute/pay that amount), and the future value will be positive (indicating money you'll have at the end).

Common Errors and Troubleshooting

When working with the PMT() function, you might encounter error messages or unexpected results. Here are some common issues and how to resolve them:

#NUM! and #VALUE! errors

The PMT() function may return these errors for several reasons:

• #NUM! typically appears when Excel cannot compute a valid result with the given inputs. This might happen if your interest rate is extremely high or your term is unusually long.

• #VALUE! usually indicates there's a problem with one of your input values, such as text where a number is expected.

Common mistakes to avoid

Forgetting to adjust rate and nper for monthly/quarterly payments

One of the most frequent mistakes is using the annual interest rate directly instead of dividing it by the number of payments per year. For example, using 5% instead of 5%/12 for monthly payments.

Incorrect: =PMT(5%, 30*12, 250000)
Correct: =PMT(5%/12, 30*12, 250000)

Inputting non-numeric values

Ensure all parameters contain numeric values or cell references to numeric values. Accidentally including text or blank cells will cause errors.

Using incorrect signs (positive instead of negative)

Remember that in financial functions, money you pay out should be negative and money you receive should be positive. If your loan amount (pv) is entered as negative, your payment will appear positive (and vice versa). For loans:

If PV is positive: PMT will be negative (you're paying out)
If PV is negative: PMT will be positive (appears as money coming in)

Mixing up the period counts

Make sure your nper (number of periods) matches your rate period. If you've adjusted your rate to a monthly figure, your periods should be in months too.

Catching these common errors will help you get accurate results when using the PMT() function for financial calculations.

Advanced Use Cases and Related Functions

The PMT() function works well alongside other financial functions in Excel to create comprehensive loan analyses and financial models. Here's how PMT() integrates with other financial functions:

IPMT (interest portion of payment)

The IPMT() function calculates the interest portion of a loan payment for a specific period. When combined with PMT(), you can see how much of each payment goes to interest.

=IPMT(rate, per, nper, pv, [fv], [type])

Returning to our $300,000 mortgage example from earlier, we can find the interest portion of the 12th payment (30-year mortgage at 4.5% annual interest):

IPMT() Function for Mortgage Loan. Image by Author.

=IPMT(4.5%/12, 12, 30*12, 300000)

This gives -$1,108.39, meaning $1,108.39 of this payment goes toward interest.

PPMT (principal portion of payment)

The PPMT() function calculates the principal portion of a loan payment for a specific period. This shows how much of your payment reduces the actual loan balance.

=PPMT(rate, per, nper, pv, [fv], [type])	

Using the same mortgage example, to find the principal portion of the 12th payment:

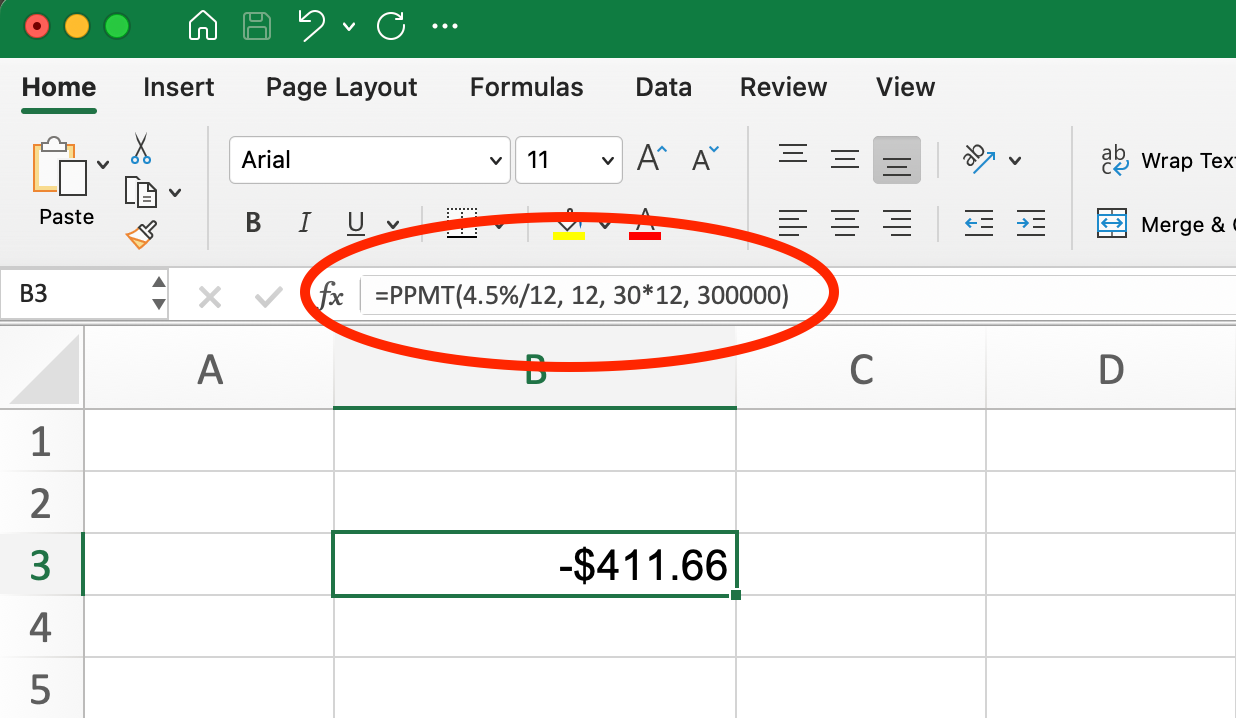
PPMT Formula for Mortgage Loan. Image by Author.

=PPMT(4.5%/12, 12, 30*12, 300000)

This returns -$411.66, showing that $411.66 goes toward reducing the loan balance.

Notice that the sum of the interest and principal portions (-$1,108.39 - $411.66 = -$1,520.05) equals approximately our total monthly payment amount. This relationship always holds true: PMT = IPMT + PPMT for any given period.

NPER (number of periods required for a loan)

If you know how much you can afford to pay monthly, NPER() helps determine how long it will take to pay off a loan:

=NPER(rate, pmt, pv, [fv], [type])

For example, if you can pay $2,000 monthly on a $300,000 loan at 4.5% annual interest:

NPER Formula for Mortgage Loan. Image by Author.

=NPER(4.5%/12, -2000, 300000)

This returns 220.86, meaning it would take approximately 221 months (about 18.4 years) to pay off the loan. This is significantly faster than the standard 30-year term because you're paying more than the minimum payment.

RATE (finding the interest rate)

When you know the loan amount, payment amount, and term, RATE() can find the interest rate:

=RATE(nper, pmt, pv, [fv], [type], [guess])	

For a $300,000 loan with $1,520.06 monthly payments over 30 years:

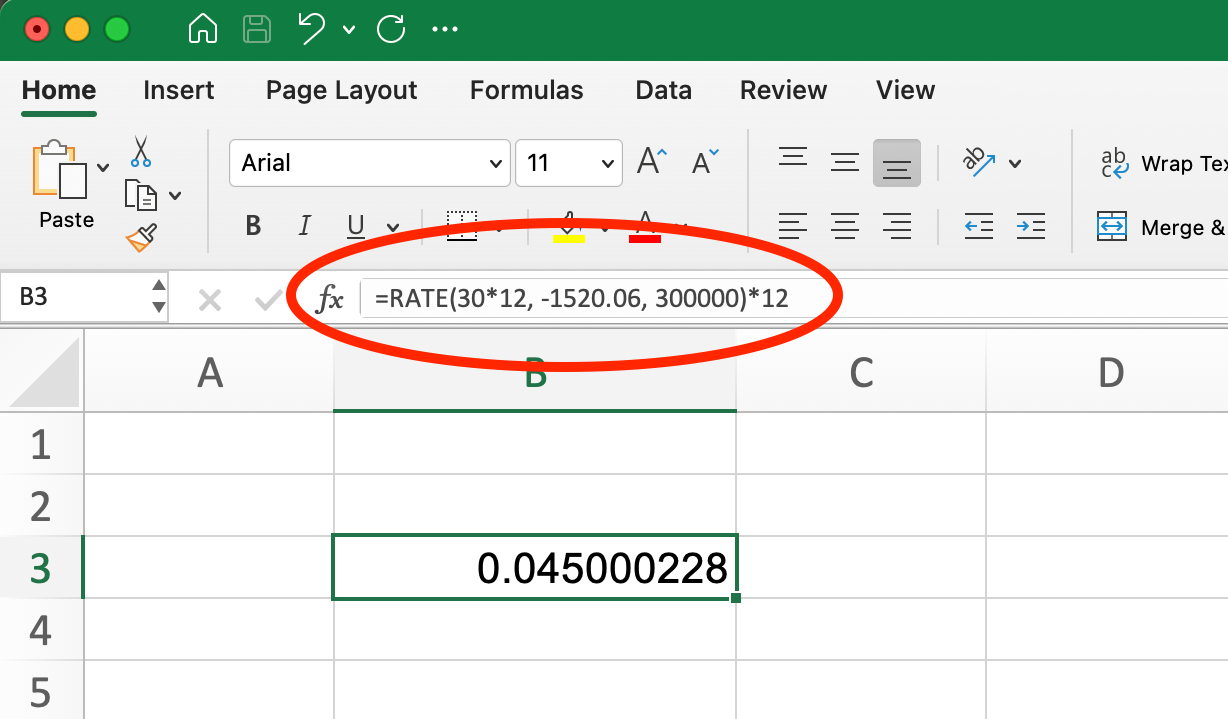
RATE Formula for Mortgage Loan. Image by Author.

=RATE(30*12, -1520.06, 300000)*12

This returns 4.5%, confirming that our monthly payment of $1,520.06 corresponds to a 4.5% annual interest rate. We multiply the result by 12 to convert the monthly rate to an annual rate.

Goal-seeking techniques

Excel's Goal Seek feature can help answer questions like:

• How much can I borrow if I can afford a specific monthly payment?
• What interest rate would I need to negotiate to keep payments below a certain amount?

For example, if we want to keep our monthly payments at $2,000 for the $400,000 mortgage from our earlier example (6% interest rate, 20-year term), we could use Goal Seek to determine how much of a down payment we would need to make. For a detailed tutorial on this subject, take a look at our guide on How to Use Goal Seek in Excel.

These integrated approaches allow for more sophisticated financial planning and decision-making beyond basic payment calculations. By combining PMT() with these related functions, you can build complete loan amortization schedules and analyze various financial scenarios.

Key Takeaways

Properly using the PMT() function in Excel requires attention to detail, especially when adjusting rates and periods. Here are the most important points to remember:

• Always adjust your interest rate and number of periods based on payment frequency. For monthly payments on an annual rate, divide the rate by 12 and multiply the years by 12.

• The PMT() function follows a specific cash flow convention: payments you make appear as negative numbers, while money you receive shows as positive.

• PMT() works as part of a family of financial functions (IPMT(), PPMT(), NPER(), RATE()) that together can create comprehensive loan and investment analyses.

• Common errors can be avoided by double-checking your inputs, ensuring you've properly adjusted for payment frequency, and using the correct signs for cash flows.

• The PMT() function isn't just for loans—it's equally valuable for savings and investment planning when you need to determine regular contribution amounts.

Excel templates that incorporate the PMT() function can save time and reduce errors when working with repeated financial calculations. Try creating a reusable template for loan comparisons or savings plans to streamline your financial analysis.

Conclusion

Applying the PMT() function in Excel provides a solid foundation for making informed financial decisions. Whether you're calculating mortgage payments, planning savings contributions, or evaluating investment opportunities, this versatile function helps you understand the financial implications of different scenarios.

By using the PMT() function with related functions like IPMT(), PPMT(), NPER(), and RATE(), you can create comprehensive financial models that answer complex questions about loans and investments. Adding Goal Seek and scenario analysis further enhances your ability to explore different financial possibilities.

If you'd like to deepen your Excel skills, we offer excellent resources to continue your learning journey:

• Our Excel Fundamentals skill track is perfect for those looking to build a comprehensive foundation in Excel, covering everything from data preparation and visualization to analysis techniques. This track requires no prior experience and guides you through practical exercises with real-world scenarios.
• For those specifically interested in financial applications, our Financial Modeling in Excel course teaches you how to work with cash flows, scenario analysis, time value of money, and capital budgeting. This intermediate-level course is taught by industry professionals and includes hands-on exercises with financial data.

With these skills and resources, you'll be well-equipped to apply the PMT() function and related Excel tools to your financial decision-making processes, creating loan amortization schedules and building sophisticated investment models.