Standardabweichung der Stichprobe: Die wichtigsten Ideen

Die Standardabweichung der Stichprobe ist ein statistisches Maß, mit dem die Schwankungen innerhalb eines Datensatzes quantifiziert werden können. Sie sagt uns insbesondere, wie stark einzelne Datenpunkte in einer Stichprobe vom Stichprobenmittelwert abweichen.

Die Standardabweichung einer Stichprobe ist in der Inferenzstatistik wichtig, wenn du Rückschlüsse auf eine bestimmte Grundgesamtheit ziehen willst, oder, wie Statistiker es ausdrücken würden, um von einer Stichprobe auf eine Grundgesamtheit zu schließen. Um diese Unterschiede zu verstehen, empfehle ich dir, die DataCamp-Kurse "Einführung in die Statistik" und " Grundlagen der Statistik" zu besuchen, um dich mit den Konzepten der Statistik vertraut zu machen. Wenn du dich ernsthaft mit Statistik beschäftigst und dich für eine Karriere in diesem Bereich interessierst, solltest du dir den DataCamp-Leitfaden How to Become a Statistician ansehen.

Was ist die Standardabweichung einer Stichprobe?

Die Standardabweichung der Stichprobe ist ein statistisches Maß, das die Variation oder Streuung in einem Datensatz quantifiziert. Die Standardabweichung der Stichprobe wird als Quadratwurzel der Stichprobenvarianz berechnet, wobei die Stichprobenvarianz die Summe der quadrierten Differenzen zum Mittelwert ist, geteilt durch den Stichprobenumfang minus eins. Wir verwenden die Standardabweichung der Stichprobe, wenn wir wissen wollen, wie stark die Datenpunkte in einer Stichprobe vom Mittelwert der Stichprobe abweichen.

Wie man die Standardabweichung einer Stichprobe berechnet

Für die Berechnung der Standardabweichung der Stichprobe verwenden wir eine bestimmte Formel.

Formel für die Standardabweichung der Stichprobe

Hier ist die Beispielformel für die Standardabweichung:

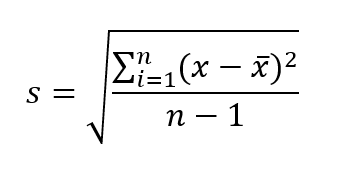
Formel für die Standardabweichung der Stichprobe. Bild vom Autor.

Wo:

• s = Standardabweichung der Stichprobe
• n = Anzahl der Datenpunkte in der Stichprobe
• x = einzelner Datenpunkt
• x̄ = Stichprobenmittelwert
• n-1 = der Korrekturfaktor für Stichprobendaten

Beachte, dass wir bei der Berechnung der Standardabweichung der Stichprobe n-1 im Nenner verwenden , um die Stichprobenverzerrung zu korrigieren. Dies wird als Bessel-Korrektur bezeichnet. Wenn wir an der Standardabweichung der Bevölkerung interessiert wären, würden wir stattdessen n im Nenner verwenden.

Wie man die Standardabweichung der Stichprobe von Hand berechnet

Gehen wir das folgende Beispiel durch, um zu sehen, wie man die Standardabweichung der Stichprobe mithilfe der Formel berechnet. Angenommen, du hast eine Datenuntermenge mit den folgenden Werten:

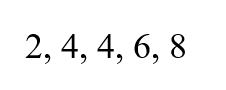
Du solltest diese Schritte befolgen:

Schritt 1: Berechne den Stichprobenmittelwert

Finde den Mittelwert der Datenpunkte.

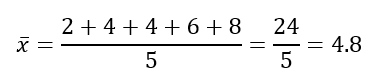
Schritt 2: Finde die quadrierten Differenzen vom Mittelwert

Subtrahiere den Mittelwert und quadriere das Ergebnis für jeden Datenpunkt

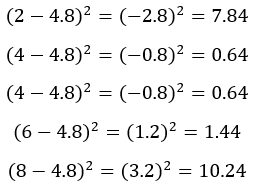
Schritt 3: Summe der quadrierten Abweichungen

Addiere die quadrierten Abweichungen vom Mittelwert.

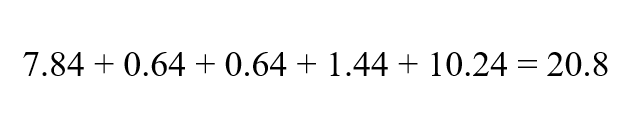
Schritt 4: Gib die berechneten Variablen in die Formel ein

Setze die Werte in die Formel ein, um die Standardabweichung der Stichprobe zu erhalten.

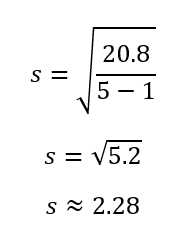
Aus der obigen Berechnung geht hervor, dass die Standardabweichung der Daten etwa 2,28 beträgt. Wenn die Berechnung der Standardabweichung der Stichprobe von Hand nicht praktikabel oder hilfreich ist und du ein Tool wie Excel verwenden musst, schau dir unsere Anleitung zur Berechnung der Standardabweichung in Excel an.

Warum die Standardabweichung der Stichprobe?

Die Stichprobenstandardabweichung ist ein bevorzugtes Maß für die Variabilität, wenn eine Schätzung der Standardabweichung der Grundgesamtheit auf der Grundlage einer Stichprobe benötigt wird. Die Bessel-Korrektur(n-1) in der Formel gleicht die Verzerrung aus und verbessert die Genauigkeit der Schätzung, da die Stichprobe die Grundgesamtheit möglicherweise nicht perfekt repräsentiert. Wenn du den Nenner verkleinerst, erhöhen sich die berechnete Varianz und Standardabweichung. Dies gleicht die Tendenz kleinerer Stichproben aus, die Variabilität zu unterschätzen.

Bedeutung der Standardabweichung der Stichprobe

Die Standardabweichung der Stichprobe ist wichtig für die Schätzung der Populationsparameter. Schauen wir uns das mal an.

Berechnung von Konfidenzintervallen 

Konfidenzintervalle können entweder mit der Standardabweichung der Stichprobe oder der Standardabweichung der Grundgesamtheit berechnet werden, je nachdem, was verfügbar ist. Wenn die Standardabweichung der Grundgesamtheit nicht bekannt ist, wird die Standardabweichung der Stichprobe verwendet und eine t-Verteilung angewandt, um den Bereich der Werte zu schätzen, der wahrscheinlich den Mittelwert der Grundgesamtheit enthält. Eine kleinere Standardabweichung von der Stichprobe oder der Grundgesamtheit führt zu einem engeren Konfidenzintervall, was auf eine höhere Genauigkeit der Schätzung hindeutet.

Hypothesenprüfung 

Bei Hypothesentests kann entweder die Standardabweichung der Stichprobe oder die Standardabweichung der Grundgesamtheit verwendet werden, je nachdem, was bekannt ist. Wenn die Standardabweichung der Grundgesamtheit nicht bekannt ist, wird die Standardabweichung der Stichprobe verwendet, und die t-Verteilung wird in der Regel zur Auswertung der Teststatistik genutzt. Wenn die Standardabweichung der Grundgesamtheit bekannt ist, wird stattdessen die z-Verteilung verwendet, die mehr Genauigkeit bietet. Eine kleinere Standardabweichung, egal ob von der Stichprobe oder der Grundgesamtheit, führt zu einem empfindlicheren Test und macht es einfacher, signifikante Unterschiede zu erkennen.

Beispielhafte Standardabweichung und verwandte Begriffe

Werfen wir einen Blick auf einige Begriffe, die mit der Standardabweichung der Stichprobe zusammenhängen. Die Verwechslung dieser Begriffe kann zu häufigen Fehlern führen. 

Standardabweichung vs. Varianz

Die Standardabweichung der Stichprobe und die Varianz messen beide die Variabilität in einem Datensatz. Allerdings drücken sie die Variabilität unterschiedlich aus. Die Varianz eines Datensatzes misst den Durchschnitt der quadrierten Unterschiede zwischen jedem Datenpunkt und dem Mittelwert. Die Varianz wird also in quadratischen Einheiten ausgedrückt. Andererseits wird die Standardabweichung als Quadratwurzel der Varianz berechnet, sodass die Standardabweichung in denselben Einheiten wie die Daten ausgedrückt wird.

Standardabweichung der Stichprobe vs. Standardabweichung der Grundgesamtheit

Schauen wir uns zwei Szenarien an, um zwischen der Standardabweichung der Stichprobe und der Standardabweichung der Grundgesamtheit zu unterscheiden.

Mit Beispieldaten arbeiten

Die Stichprobenstandardabweichung wird verwendet, wenn du eine Teilmenge einer großen Grundgesamtheit verwendest. Stell dir vor, du führst eine Umfrage zur Kundenzufriedenheit für ein Einzelhandelsunternehmen durch. Du sammelst Antworten von etwa 200 Kunden, um Rückschlüsse auf die Zufriedenheit der Kunden der Einzelhandelskette zu ziehen. In diesem Fall verwendest du die Standardabweichung der Stichprobe für Rückschlüsse, da du mit einer Teilmenge einer großen Grundgesamtheit arbeitest.

Arbeiten mit Bevölkerungsdaten

Die Standardabweichung der Grundgesamtheit ist geeignet, wenn du die vollständigen Daten für eine ganze Grundgesamtheit hast. In diesem Fall brauchst du die Verzerrung nicht zu berücksichtigen, da jeder Datenpunkt berücksichtigt wird. Stell dir vor, du bist die Personalabteilung eines Unternehmens mit 50 Mitarbeitern und möchtest die Schwankungen ihrer Gehälter berechnen. Du verwendest die Standardabweichung der Grundgesamtheit, da du das Gehalt für jeden Arbeitnehmer kennst.

Beispielhafte Standardabweichung in Python und R

Wenn du R zur Berechnung der Standardabweichung verwendest, berechnet die Funktion sd() die Standardabweichung der Stichprobe standardmäßig mit n-1 im Nenner.

# Sample standard deviation
data <- c(10, 12, 15, 18, 20)
sample_sd <- sd(data)
print(round(sample_sd, 2))

4.12

Python-Pakete wie NumPy und Pandas gehen jedoch von der Standardabweichung der Grundgesamtheit aus, sofern nicht anders angegeben. Zum Beispiel verwendet numpy.std() standardmäßig n im Nenner und behandelt die Daten wie eine Grundgesamtheit. 

# Import numpy library
import numpy as np
data = [10, 12, 15, 18, 20]
population_sd = np.std(data)  # Population standard deviation
print(round(population_sd, 2))

3.69

Wenn du stattdessen die Standardabweichung der Stichprobe haben möchtest, kannst du ddof=1 übergeben, um die Freiheitsgrade zu berücksichtigen.

sample_sd = np.std(data, ddof=1)  # Sample standard deviation
print(round(sample_sd, 2))

4.12

Wenn du mit Statistik in einer Programmierumgebung arbeitest, empfehle ich dir unseren Kurs Statistical Inference with R oder den Kurs Foundations of Inference in Python, um dir ein Grundwissen anzueignen. 

Fazit

Die Standardabweichung der Stichprobe ist ein wichtiges statistisches Maß, um Abweichungen zu quantifizieren und Rückschlüsse zu ziehen. Wenn du deine Kenntnisse in Statistik und Datenanalyse vertiefen möchtest, empfehle ich dir die DataCamp-Karriereschienen Data Analyst with R und Data Analyst with Python, die umfassende, branchenrelevante Kenntnisse vermitteln. Unser Kurs "Datenanalyse in Excel" ist auch geeignet, wenn du Geschäftsanalytiker/in werden willst, der/die sich darauf konzentriert, datengestützte Entscheidungen zu treffen.