Desviación típica de la muestra: Las ideas clave

La desviación típica muestral es una medida estadística utilizada para cuantificar la variación dentro de un conjunto de datos. Concretamente, nos dice cuánto difieren los puntos de datos individuales de una muestra de la media muestral.

La desviación típica de la muestra es importante en estadística inferencial si quieres sacar conclusiones sobre una población determinada o, como dirían los estadísticos, hacer inferencias de una muestra a una población. Para comprender estas distinciones, te recomiendo que sigas los cursos Introducción a la Estadística y Estadística Básica de DataCamp para familiarizarte con los conceptos estadísticos. Como nota final, si te tomas en serio la estadística y estás interesado en una carrera profesional utilizando la estadística, consulta la guía de DataCamp sobre Cómo convertirse en estadístico.

¿Qué es la desviación típica de la muestra?

La desviación típica muestral es una medida estadística que cuantifica la variación o dispersión de un conjunto de datos. La desviación típica de la muestra se calcula como la raíz cuadrada de la varianza de la muestra, donde la varianza de la muestra es la suma de las diferencias al cuadrado respecto a la media, dividida por el tamaño de la muestra menos uno. Utilizamos la desviación típica muestral cuando queremos saber cuánto difieren los puntos de datos de una muestra de la media muestral.

Cómo calcular la desviación típica de la muestra

Utilizamos una fórmula específica para calcular la desviación típica de la muestra.

Fórmula para la desviación típica de la muestra

Aquí tienes la fórmula de la desviación típica de muestra:

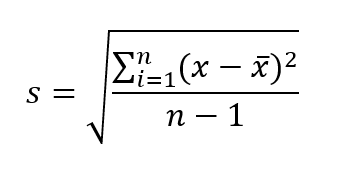
Fórmula de la desviación típica de la muestra. Imagen del autor.

Dónde:

• s = desviación típica de la muestra
• n = número de puntos de datos de la muestra
• x = punto de datos individual
• x̄ = media muestral
• n-1 = el factor de corrección para los datos de la muestra

Ten en cuenta que al calcular la desviación típica de la muestra, utilizamos n-1 en el denominador para corregir el sesgo de la muestra. Esto se conoce como corrección de Bessel. Si nos interesara la desviación típica de la población, utilizaríamos n en el denominador .

Cómo calcular a mano la desviación típica muestral

Veamos en el siguiente ejemplo cómo calcular la desviación típica muestral utilizando la fórmula. Supón que tienes un subconjunto de datos con los siguientes valores:

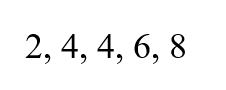
Debes seguir estos pasos:

Paso 1: Calcula la media muestral

Halla la media de los puntos de datos.

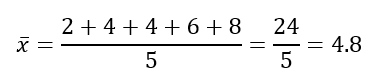
Paso 2: Halla las diferencias al cuadrado respecto a la media

Resta la media y eleva al cuadrado el resultado de cada punto de datos

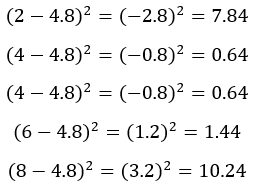
Paso 3: Suma las desviaciones al cuadrado

Suma las diferencias al cuadrado respecto a la media.

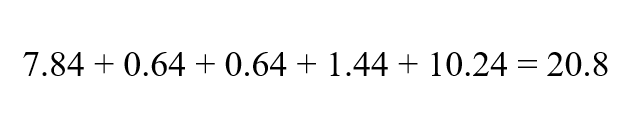
Paso 4: Introduce las variables calculadas en la fórmula

Sustituye los valores en la fórmula para obtener la desviación típica muestral.

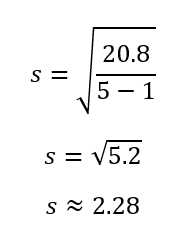
A partir del cálculo anterior, vemos que la desviación típica de los datos es de aproximadamente 2,28. Ahora bien, si calcular la desviación típica muestral a mano no te resulta práctico ni útil, y necesitas utilizar una herramienta como Excel, consulta nuestro tutorial sobre Cómo calcular la desviación típica en Excel.

¿Por qué utilizar la desviación típica muestral?

La desviación típica de la muestra es una medida preferida de la variabilidad cuando se necesita una estimación de la desviación típica de la población basada en una muestra. La corrección de Bessel(n-1) en la fórmula ajusta el sesgo y mejora la precisión de la estimación, ya que la muestra puede no representar perfectamente a la población. Si el denominador es menor, aumentan la varianza y la desviación típica calculadas. Esto compensa la tendencia de las muestras más pequeñas a subestimar la variabilidad.

Importancia de la desviación típica de la muestra

La desviación típica de la muestra es importante para estimar los parámetros de la población. Echemos un vistazo.

Cálculo de intervalos de confianza 

Los intervalos de confianza pueden calcularse utilizando la desviación típica de la muestra o la desviación típica de la población, según cuál esté disponible. Si se desconoce la desviación típica de la población, se utiliza la desviación típica de la muestra y se aplica una distribución t para estimar el intervalo de valores que probablemente contenga la media de la población. Una desviación típica menor de la muestra o la población conduce a un intervalo de confianza más estrecho, lo que indica una mayor precisión en la estimación.

Comprobación de hipótesis 

En las pruebas de hipótesis, se puede utilizar la desviación típica de la muestra o la desviación típica de la población, dependiendo de cuál se conozca. Si se desconoce la desviación típica de la población, se aplica la desviación típica de la muestra, y se suele utilizar la distribución t para evaluar la estadística de la prueba. Cuando se conoce la desviación típica de la población, se utiliza en su lugar la distribución z, que proporciona más precisión. Una desviación típica menor, ya sea de la muestra o de la población, da lugar a una prueba más sensible, que facilita la detección de diferencias significativas.

Desviación típica de la muestra y términos relacionados

Veamos algunos términos relacionados con la desviación típica muestral. Confundir estos términos puede conducir a errores comunes. 

Desviación típica frente a varianza

Tanto la desviación típica de la muestra como la varianza miden la variabilidad de un conjunto de datos. Sin embargo, expresan la variabilidad de forma diferente. La varianza de un conjunto de datos mide la media de las diferencias al cuadrado entre cada punto de datos y la media. Así, la varianza se expresa en unidades al cuadrado. En cambio, la desviación típica se calcula como la raíz cuadrada de la varianza, por lo que la desviación típica se expresa en las mismas unidades que los datos.

Desviación típica de la muestra vs. desviación típica de la población

Veamos dos supuestos que nos ayudarán a diferenciar entre desviación típica muestral y desviación típica poblacional.

Trabajar con datos de muestra

La desviación típica muestral se utiliza cuando utilizas un subconjunto de una población grande. Imagina que estás realizando una encuesta de satisfacción del cliente para una empresa minorista. Recoges las respuestas de unos 200 clientes para hacer inferencias sobre la satisfacción de la clientela de la cadena minorista. En este caso, utilizarás la desviación típica muestral para hacer inferencias, ya que estás trabajando con un subconjunto de una población grande.

Trabajar con datos de población

La desviación típica poblacional es adecuada cuando tienes los datos completos de toda una población. En este caso, no necesitarás tener en cuenta el sesgo, ya que se tendrían en cuenta todos los puntos de datos. Ahora, imagina que eres el RRHH de una empresa con 50 empleados y quieres calcular la variabilidad de sus salarios. Utilizarás la desviación típica de la población, ya que conoces el salario de cada empleado.

Muestra de desviación estándar en Python y R

Cuando se utiliza R para calcular la desviación típica, la función sd() calcula por defecto la desviación típica de la muestra con n-1 en el denominador.

# Sample standard deviation
data <- c(10, 12, 15, 18, 20)
sample_sd <- sd(data)
print(round(sample_sd, 2))

4.12

Sin embargo, los paquetes de Python como NumPy y Pandas asumen la desviación típica de la población a menos que se especifique lo contrario. Por ejemplo, numpy.std() utiliza n en el denominador por defecto, tratando los datos como una población. 

# Import numpy library
import numpy as np
data = [10, 12, 15, 18, 20]
population_sd = np.std(data)  # Population standard deviation
print(round(population_sd, 2))

3.69

Si quieres la desviación típica muestral en su lugar, puedes pasar ddof=1 para ajustar los grados de libertad.

sample_sd = np.std(data, ddof=1)  # Sample standard deviation
print(round(sample_sd, 2))

4.12

Si trabajas con estadística en un entorno de programación, te recomendaría nuestro curso de habilidades Inferencia estadística con R o el curso Fundamentos de la inferencia en Python para desarrollar un conjunto básico de habilidades. 

Conclusión

La desviación típica de la muestra es una medida estadística importante para cuantificar la variación y hacer inferencias. Si quieres avanzar en tus conocimientos de estadística y análisis de datos, te recomiendo que eches un vistazo a los itinerarios profesionales de Analista de Datos con R y Analista de Datos con Python de DataCamp, que ofrecen conocimientos exhaustivos y relevantes para el sector. Nuestro curso de Análisis de Datos en Excel también es adecuado si quieres convertirte en un analista empresarial centrado en la toma de decisiones basadas en datos.